Траекторные измерения

1. Траекторные измерения

1

2.

1 Фотограмметрия
2 Оптические системы
3 Комплексная обработка информации
2

3.

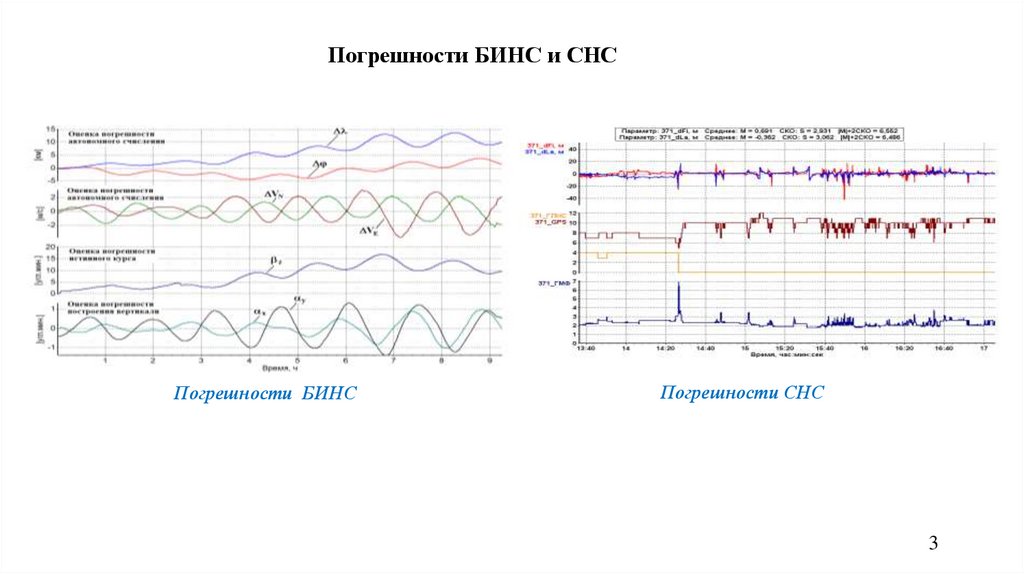
Погрешности БИНС и СНС
Погрешности БИНС
Погрешности СНС
3

4.

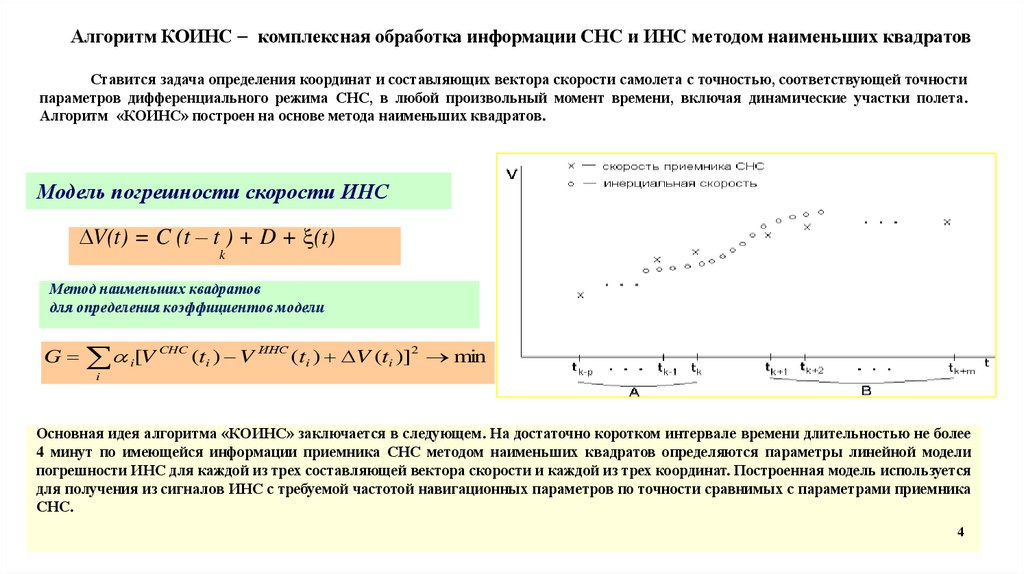
Алгоритм КОИНС комплексная обработка информации СНС и ИНС методом наименьших квадратов
Ставится задача определения координат и составляющих вектора скорости самолета с точностью, соответствующей точности
параметров дифференциального режима СНС, в любой произвольный момент времени, включая динамические участки полета.
Алгоритм «КОИНС» построен на основе метода наименьших квадратов.
Модель погрешности скорости ИНС
V(t) = C (t – t ) + D + (t)
k
Метод наименьших квадратов
для определения коэффициентов модели
G i[V CHC (ti ) V ИНС (ti ) V (ti )]2 min
i
Основная идея алгоритма «КОИНС» заключается в следующем. На достаточно коротком интервале времени длительностью не более
4 минут по имеющейся информации приемника СНС методом наименьших квадратов определяются параметры линейной модели
погрешности ИНС для каждой из трех составляющей вектора скорости и каждой из трех координат. Построенная модель используется
для получения из сигналов ИНС с требуемой частотой навигационных параметров по точности сравнимых с параметрами приемника
СНС.
4

5.

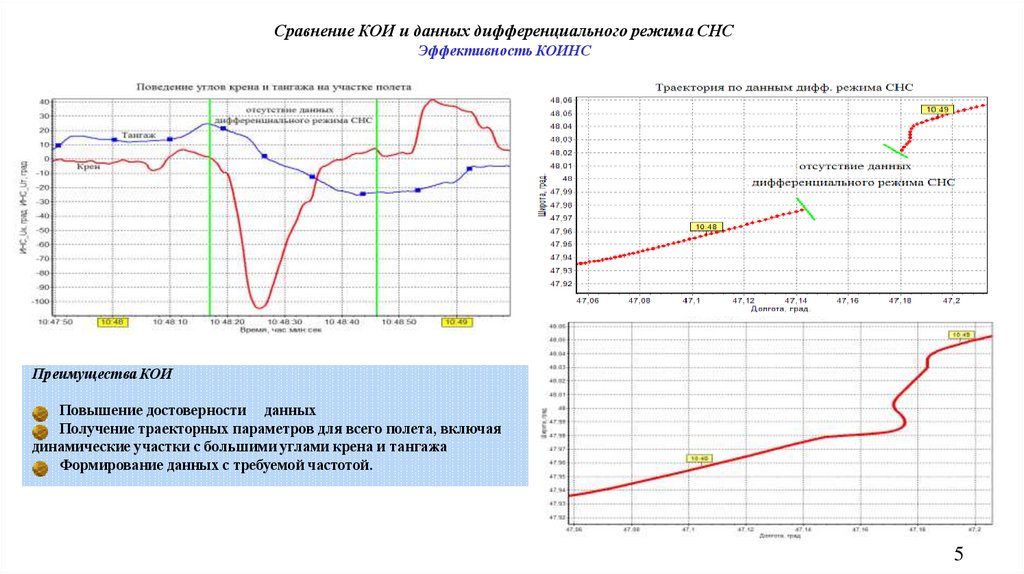
Сравнение КОИ и данных дифференциального режима СНС
Эффективность КОИНС
Преимущества КОИ
Повышение достоверности данных
Получение траекторных параметров для всего полета, включая
динамические участки с большими углами крена и тангажа
Формирование данных с требуемой частотой.
5

6.

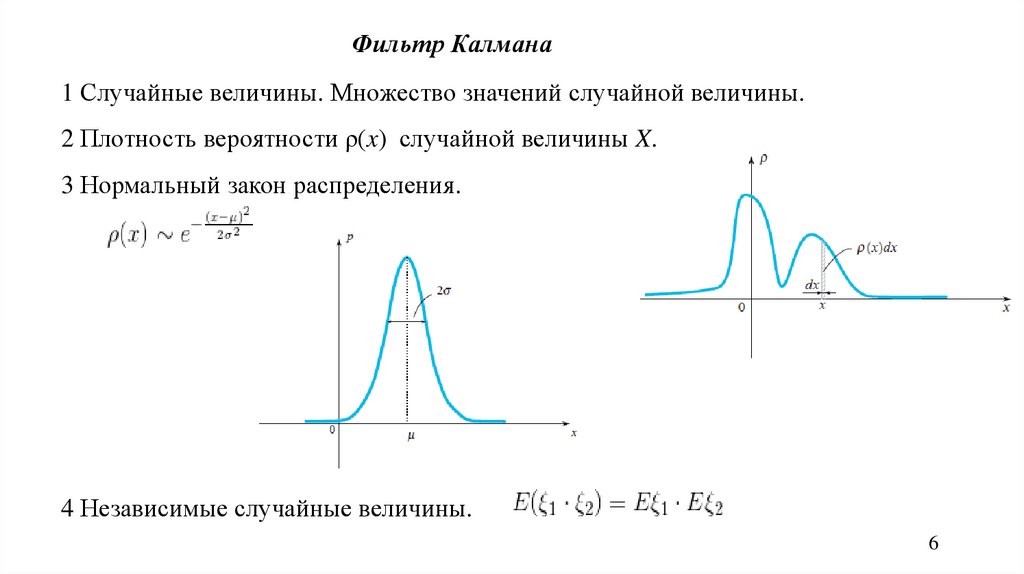
Фильтр Калмана
1 Случайные величины. Множество значений случайной величины.
2 Плотность вероятности ρ(x) случайной величины X.
3 Нормальный закон распределения.
4 Независимые случайные величины.
6

7.

Задача Для каждого момента времени tk определить координату x.
Закон изменения координаты выглядит так:
,
где ξk – шум. Величину vkdt обозначим через uk.
Уравнение наблюдения за объектом:
,
где ηk – ошибка наблюдения.
Уравнение для координаты и уравнение наблюдения выглядят так:
7

8.

Предположения
1
uk – известная величина, которая контролирует эволюцию системы.
2
Ошибка модели ξk и ошибка наблюдения ηk – случайные величины, их законы
распределения не зависят от времени tk.
3 Средние значения ошибок равны нулю.
4
Законы распределения случайных величин ξk и ηk могут быть нам и не известны,
но известны их дисперсии
и
.
5
Предполагается, что все случайные ошибки независимы между собой.
8

9.

Алгоритм Калмана
Рассуждаем по индукции. Пусть на k-ом уже найдены отфильтрованное значение
,
которое хорошо приближает действительную координату xk объекта.
Из уравнения движения
можно предположить, что на (k+1)-ом шаге
действительную координату xk+1 близка к
. С другой стороны, на (k+1)-ом
шаге имеется неточное наблюдение zk+1 .
Идея Калмана – получить наилучшее приближение к действительной координате xk+1.
Коэффициент K называют коэффициентом Калмана, он зависит от шага итерации k+1.
Для нахождения коэффициента Калмана K следует минимизировать ошибку
9

10.

Ошибку можно представить в виде
Доказательство
Выбираем критерий оптимальности
Отсюда
Приравниваем к нулю производную по K.
Подставив значение K в формулу для среднего квадрата ошибки, получим
10

11.

Соберем все формулы
вместе.
11

12.

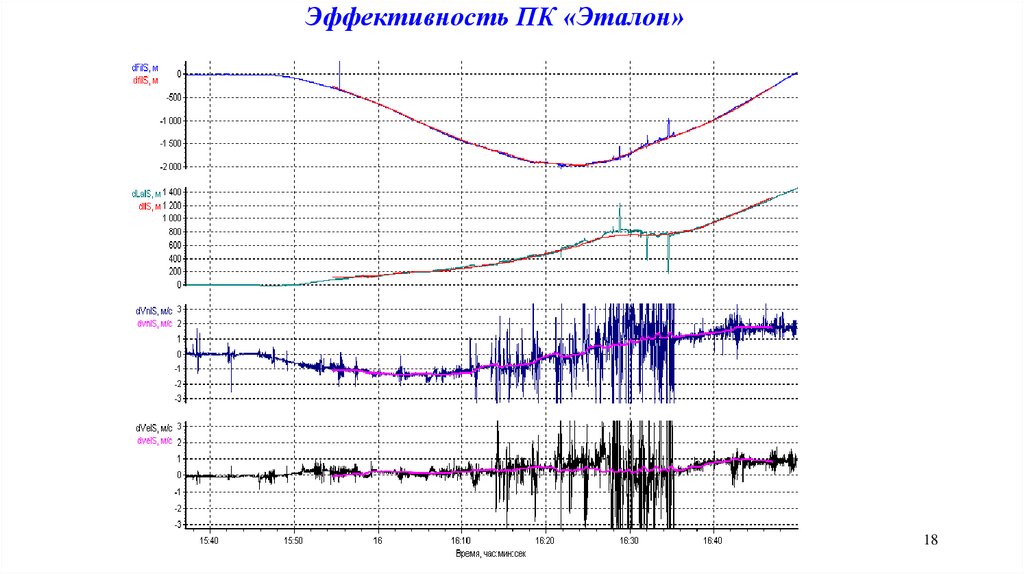
Программный комплекс оптимальной обработки «Эталон»
Направления применения алгоритмов КОИ
Обеспечение эталонных траекторных измерений при летных испытаниях ЛА и БО.
Использование ПК «Эталон» и «Коинс».
2. Анализ
характеристик инерциальных и радионавигационных систем по
материалам летных испытаний:
• в темпе полета;
• в послеполетной обработке.
Использование ПК «Эталон»
3. Реализация в вычислителях пилотажно – навигационных комплексов ЛА:
• на основе алгоритма КОИ с использованием фильтра Калмана;
• на основе алгоритма КОИ с использованием метода наименьших квадратов.
На основе ПК «Эталон» и «Коинс».
12

13.

Семейство программных комплексов «Эталон»
ПК разработки АО «ЛИИ им. М.М. Громова»
ПМО обработки и анализа материалов испытаний БИНС
Программный комплекс «Пересчет» – пересчет параметров бортового оборудования (БИНС, СНС и др.) в
различные системы координат ЛА.
Программный
комплекс «Анализ» – экспресс–оценка функционирования, оценка точностных и
статистических характеристик погрешностей БИНС.
Программные комплексы «Эталон», «Эталон-XXI» и «Эталон-МК» – оптимальная обработка
информации с разделением суммарных ошибок ИНС/БИНС на составляющие и оценкой
инструментальных погрешностей базовых элементов, вычисление эталонных значений параметров:
─ ПК «Эталон» - исходный вариант (1987г.);
─ ПК «Эталон-XXI» - разработан автором (2008г.), модернизация ПК «Эталон», предназначен для
обеспечения испытаний навигационных систем современных и перспективных ЛА;
─ ПК «Эталон-МК» - (2014г.) модернизация ПК «Эталон» с применением алгоритмов, учитывающих
неортогональности осей приборного трехгранника БИНС, предназначен для обеспечения
испытаний маневренных ЛА.
13

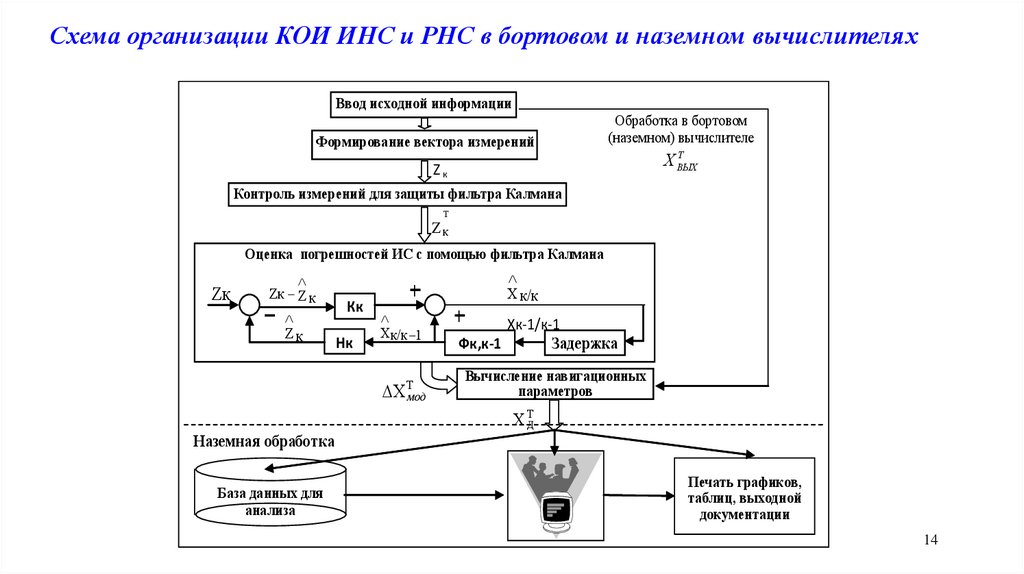
14.

Схема организации КОИ ИНС и РНС в бортовом и наземном вычислителях
Ввод исходной информации
Формирование вектора измерений
Обработка в бортовом
(наземном) вычислителе
Zк
Т
Х ВЫХ
Контроль измерений для защиты фильтра Калмана
Т
Zк
Оценка погрешностей ИС с помощью фильтра Калмана
Zк
Zк Z к
Zк
Кк
Нк
Х к/к
Х к/к 1
Х Тмод
Фк,к-1
Хк-1/к-1
Задержка
Вычисление навигационных
параметров
Х ТД
Наземная обработка
База данных для
анализа
Печать графиков,
таблиц, выходной
документации
14

15.

Оценка вектора состояния ИНС и БИНС в ПК «Эталон»
Вектор состояния модели погрешностей БИНС ΔХ Тмод
Х
Т
м од
(17×1)
[ S X , SY , VX , VY , X , Y , Z , 1S , 2 S , 3S , 1 , 2 , 3 , 4 , f1 , f 2 , f 3 ]
Вектор измерений
Zk T [ S Xиз , SYиз , V Xиз , VYиз ]
Вектор выходных параметров
Т
Х ВЫХ
[ д , д ,V д ,V д , д ,УС д ]
Уравнения фильтра Калмана:
X k / k X k / k 1 K k ( Z k H k X k / k 1 )
X k / k 1 k , k 1 X k 1 / k 1
K k Pk / k 1 H kT ( H k Pk / k 1 H kT Rk ) 1
Pk / k 1 k , k 1 Pk 1 / k 1 Tk , k 1 B k Q k B kT
Pk / k [ E K k H k ]Pk / k 1
15

16.

Модель погрешностей БИНС
Система дифференциальных уравнений, описывающая модель погрешностей БИНС,
может быть записана в следующем виде:
&
r1 V1 3V2
&
r2 V2 3V1
&
V1 2U 3 V2 а x3 2 f1 d11 f 2 d12 f 3 d13
&
V2 2U 3 V1 a x3 1 f1 d 21 f 2 d 22 f 3 d 23
r V
&
1 U 3 1 2 U 3 2 1 d11 2 d12 3d13 12 z 2 d11 13 z 3d11
R1 R2
21 z1d12 23 z3d12 31 z1d13 32 z 2 d13
U r V
&
2 3 2 1 U 3 1 1 d 21 2 d 22 3 d 23 12 z 2 d 21 13 z 3d 21
R2
R1
21 z1d 22 23 z3d 22 31 z1d 23 32 z 2 d 23
& x1 r1 x 2 r2
3
x 2 1 x1 2 1 d 31 2 d 32 3 d 33 12 z 2 d 31 13 z 3 d 31
R1
R2
21 z1d 32 23 z3d 32 31 z1d 33 32 z 2 d 33
&
&
&
1 2 3 0
&
&
&
f1 f 2 f 3 0,
&
ij 0.
16

17.

Здесь: R , R – радиусы кривизны сечений земного эллипсоида по осям расчетной
1 2
гироплатформы:
R =a/(1-0,5℮2sin2φ+℮2cos2φcos 2ε-H/a)
1
R =a/(1-0,5℮2sin2 φ+℮2 cos2 φsin2 ε-H/a)
2
d – элементы матрицы направляющих косинусов координатного преобразования систем
ij
координат, связанных с осями приборного трехгранника БИНС и моделируемой
гироплатформы, взаимное положение которых определяется углами крена , тангажа самолета
и гироскопического курса . Гироскопический курс отсчитывается от первой оси расчетной
г
платформы по часовой стрелке.
17

18. Эффективность ПК «Эталон»

18