Теория оценивания. Оптимальные наблюдатели (Фильтры Калмана)

1.

МГТУ имени Н.Э. Баумана
Кафедра ИУ-1 «Системы автоматического управления»
Теория оценивания
Оптимальные наблюдатели
(Фильтры Калмана)
Андрей Леонидович Масленников
[email protected]
2022 г.

2
Фильтры Калмана
Kalman Filters
Фильтры Калмана — семейство методов
оценивания вектора состояния по получаемым
измерениям в режиме реального времени моделях
подобного вида (пример дискретной системы):
x k 1 f x k , u k k
y k h x k k
Виды фильтра Калмана
• линейный фильтр Калмана (KF);
(гибридный, фильтр Калмана-Бюси)
• расширенный фильтр Калмана (EKF);
(дискретный, непрерывно-дискретный,
непрерывный)
(модификации: итерационный, робастный,
инвариантный)
• сигма-точечный фильтр Калмана (UKF).
Линейный фильтр Калмана — это оптимальный
наблюдатель по текущему измерению для системы:
x k 1 A k x k B k u k k
y k Ck x k Dk u k k
где стохастические процессы:
k ~N 0, Q k
k ~N 0, R k
обладают следующими характеристиками:
E T Q ковариационная матрица
E T R ковариационная матрица
E T 0 взаимная ковариационная матрица

3.

Фильтры Калмана
3
Линейный фильтр Калмана. Инициализация начальных условий. Алгоритм формирования оценок
Обозначения:
xˆ n|m - априорная оценка в момент времени по
измерениям;
- апостериорная оценка в момент времени ;
xˆ k |k
Pn|m - априорная ковариация ошибок;
Pk |k - апостериорная ковариация ошибок.
Инициализация начальных условий:
x m P
T
0
x0
xˆ k |k 1 A k xˆ k 1|k 1 B k u k
T
P
A
P
A
k |k 1
k k 1|k 1 k Q k
Апостериорная оценка:
z k y k Ck xˆ k |k 1
S k Ck Pk |k 1CTk R k
x0 E x0 m x0
P0 E x0 m x0
Априорная оценка:
x0
K k Pk |k 1CTk S k 1
xˆ k |k xˆ k|k 1 K k z k
Pk |k I K k Ck Pk |k 1 I K k Ck K k R k K Tk
T
Фильтр Калмана состоит из двух шагов на каждом такте:
прогноз (априорная оценка) и корректировка
(апостериорная оценка)

4.

5.

5
Фильтры Калмана
Фильтр Калмана-Бюси. Гибридный фильтр Калмана
Фильтр Калмана-Бюси
Это полностью непрерывный
Калмана для системы:
аналог
фильтра
x t A t x t B t u t t
y t C t x t D t u t t
Оценка требует интегрирования двух
дифференциальных уравнений:
x t A t x t B t u t K t z t
P t A t P t P t AT Q t K t R t K T t
где:
z t y t C t xˆ t
K t P t C t R
T
1
и - матрицы спектральной плотности мощности
Уравнение - частный случай матричного уравнения
Риккати
Гибридный фильтр Калмана
Это фильтр Калмана для оценки вектора состояния
непрерывной системы по дискретным измерениям,
т.е. модель системы:
x t A t x t B t u t t
y k Ck x k t
где:
x k x tk
t ~N 0, Q t
k ~N 0, R k
Инициализация начальных условий:
xˆ 0|0 E x t0
P0|0 VAR x t0

6.

6
Фильтры Калмана
Гибридный фильтр Калмана. Алгоритм формирования оценок
Априорная оценка:
x t A t x t B t u t
при xˆ tk 1 xˆ k 1|k 1
T
P t A t P t P t A Q t при P tk 1 Pk 1|k 1
Интегрируя два дифференциальных уравнения получаем:
xˆ k |k 1 xˆ tk
Pk |k 1 P tk
Апостериорная оценка (идентична дискретному ФК):
K k Pk |k 1C C Pk |k 1C R k
T
k
T
k
T
k
Проблемы использования линейного фильтра
Калмана:
только для линейных моделей;
если модель не истинна или начальные условия
определены не верно, то оценка может сильно
отличаться от истины;
сложно определять матрицы и ;
(частично решается с помощью методов
адаптивной калмановской фильтрации)
малость может привести к вычислению с ;
(решение через декомпозицию, например )
фильтр Калмана-Бюси физически не реализуем.
1
xˆ k |k xˆ k |k 1 K k y k Ck xˆ k|k 1
Pk |k I K k Ck Pk |k 1 I K k Ck K k R k K
T
T
k
Частичное решение этих проблем - расширенный
фильтра Калмана
(для нелинейных моделей)

7.

7
Фильтры Калмана
Расширенный фильтр Калмана
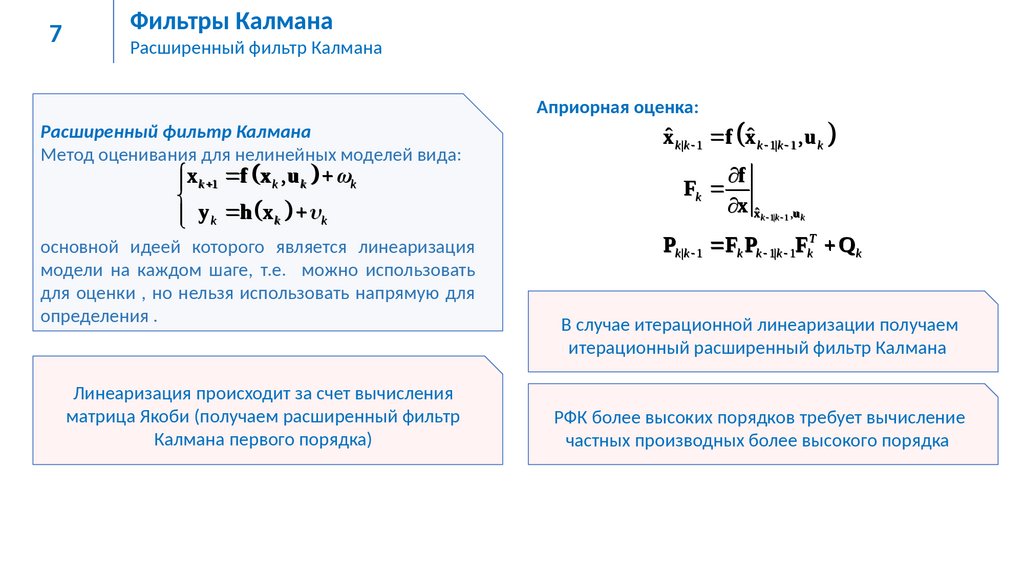
Расширенный фильтр Калмана
Метод оценивания для нелинейных моделей вида:
x k 1 f x k , u k k
y k h x k k
основной идеей которого является линеаризация
модели на каждом шаге, т.е. можно использовать
для оценки , но нельзя использовать напрямую для
определения .
Линеаризация происходит за счет вычисления
матрица Якоби (получаем расширенный фильтр
Калмана первого порядка)
Априорная оценка:
xˆ k |k 1 f xˆ k 1|k 1 , u k
Fk
f
x xˆ k 1|k 1 ,uk
Pk |k 1 Fk Pk 1|k 1FkT Q k
В случае итерационной линеаризации получаем
итерационный расширенный фильтр Калмана
РФК более высоких порядков требует вычисление
частных производных более высокого порядка

8.

Фильтры Калмана
8
Расширенный фильтр Калмана. Алгоритм формирования оценок
Апостериорная оценка:
z k y k h(x k |k 1 )
Hk
h
x x k|k 1
Виды расширенного фильтра Калмана
полностью непрерывный EKF;
гибридный EKF.
S k H k Pk |k 1H Tk R k
Все аналогично линейному фильтру Калмана, за
исключением нелинейных и линеаризации системы
на каждом шаге
K k Pk |k 1H Tk S k 1
Для полностью непрерывного EKF:
xˆ k |k xˆ k |k 1 K k z k
F(t )
Pk |k (I K k H k )Pk |k 1 (I K k H k )T K k R k K kT
EKF не оптимален по определению
(оптимален только в случае истинной линейной
модели)
f
x x ( t ),u ( t )
H (t )
h
x x ( t )
Для гибридного EKF:
F(t )
f
x x ( t ),u ( t )
Hk
h
x x k|k 1

9.

9
Фильтры Калмана
Сигма-точечный фильтр Калмана. Весовые коэффициенты
Вычисление весовых коэффициентов:
Сигма-точечный фильтр Калмана
Метод оценивания для нелинейных моделей вида:
x k 1 f (x k , u k ) k
y k h(x k ) k
основной идеей которого является линеаризация
модели
(методом
сигма-точечечного
преобразования) на каждом шаге.
UKF призван повысить устойчивость EKF, но на
практике, ввиду линеаризации, все
равно возможна неустойчивость алгоритма
где:
2 ( L ) L
W0x
L
W0C
(1 2 )
L
1
Wi C Wi x
2( L )
- масштабный коэффициент;
- масштабный коэффициент (обычно принимается
равным нулю);
- коэффициент, характеризует разброс сигма-точек
относительно ;
- коэффициент, характеризующий информацию о
распределении ;
Обычно: для нормального распределения,

10.

10
Фильтры Калмана
Сигма-точечный фильтр Калмана. Алгоритм формирования оценок
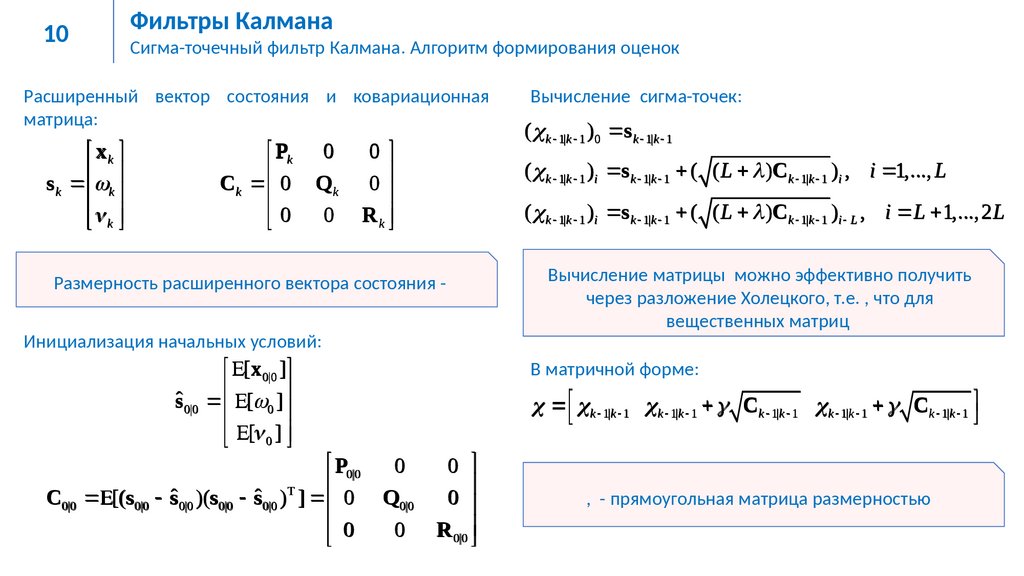
Расширенный вектор состояния и ковариационная
матрица:
xk
s k k
k
Pk
C k 0
0
0
Qk
0
0
0
R k
( k 1|k 1 )i s k 1|k 1 ( ( L )Ck 1|k 1 )i L , i L 1,..., 2 L
Инициализация начальных условий:
P0|0
0
C0|0 [(s0|0 sˆ 0|0 )(s0|0 sˆ 0|0 )T ] 0 Q0|0
0
0
( k 1|k 1 )0 s k 1|k 1
( k 1|k 1 )i s k 1|k 1 ( ( L )Ck 1|k 1 )i , i 1,..., L
Размерность расширенного вектора состояния -
[x 0|0 ]
sˆ 0|0 [ 0 ]
[ 0 ]
Вычисление сигма-точек:
Вычисление матрицы можно эффективно получить
через разложение Холецкого, т.е. , что для
вещественных матриц
В матричной форме:
k 1|k 1 k 1|k 1 Ck 1|k 1 k 1|k 1 Ck 1|k 1
0
0
R 0|0
, - прямоугольная матрица размерностью

11.

12.

12
Фильтры Калмана
Сигма-точечный фильтр Калмана. Алгоритм формирования оценок
Апостериорная оценка расширенного вектора состояния:
x k |k
sˆ k |k [ k ]
[ k ]
xˆ 0|0 [x0|0 ]
P0|0 [(x0|0 xˆ 0|0 )(x0|0 xˆ 0|0 )T ]
Апостериорная оценка расширенной ковариационной
матрицы:
Pk |k
Ck |k 0
0
0
Rk
0
Инициализация начальных условий:
0
0
Q k
При и алгоритм можно упростить,
что разделит вычисление сигма-точек на два этапа
Вычисление сигма-точек:
k 1|k 1 [x k 1|k 1 x k 1|k 1 Pk 1|k 1 xk 1|k 1 Pk 1|k 1 ]
k* 1|k 1 F( k 1|k 1 , u k 1 )

13.

Фильтры Калмана
13
Сигма-точечный фильтр Калмана. Случай E[

English Русский Правила