Погрешности измерений

1. Погрешности измерений

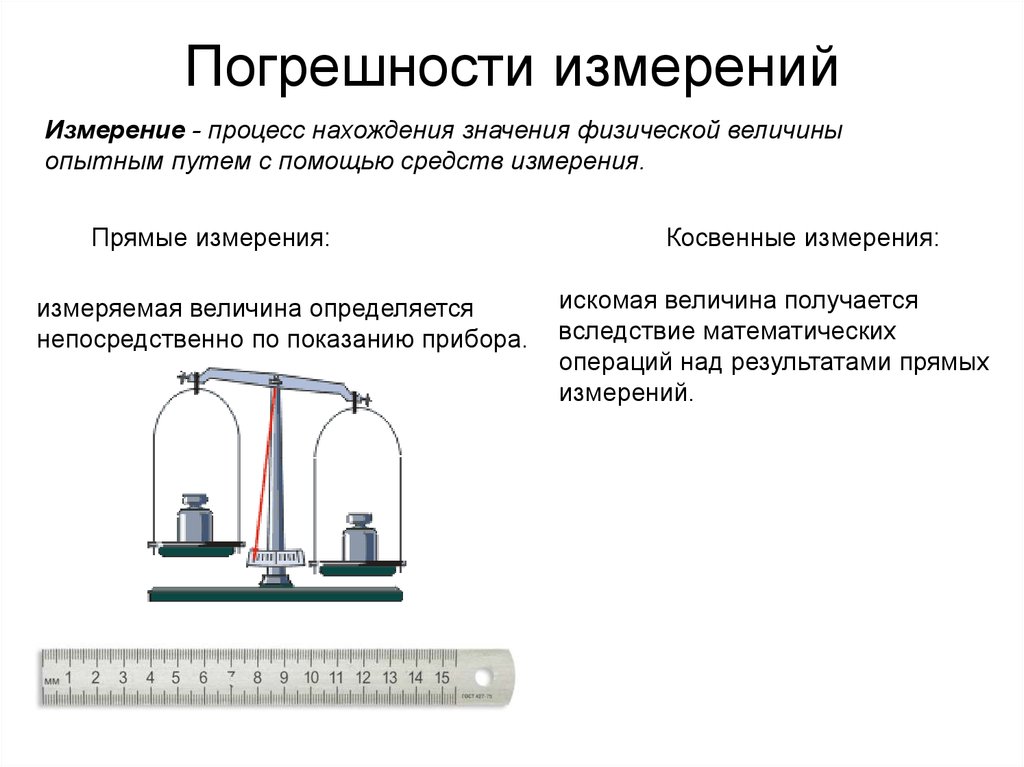
Измерение - процесс нахождения значения физической величины
опытным путем с помощью средств измерения.
Прямые измерения:
измеряемая величина определяется
непосредственно по показанию прибора.
Косвенные измерения:
искомая величина получается
вследствие математических
операций над результатами прямых
измерений.

2. ПОГРЕШНОСТИ ПРЯМЫХ ИЗМЕРЕНИЙ

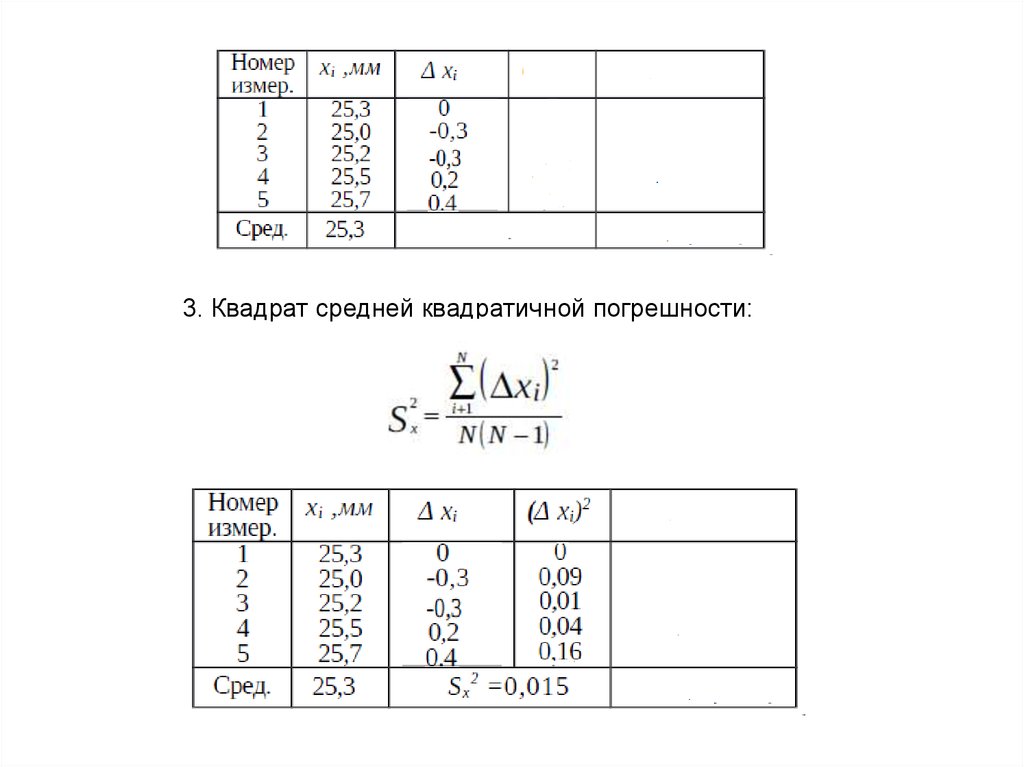
1. Среднее значение измеряемой величины x:
x1 x2 .... x N
x
N
2. Абсолютные погрешности измерений:
x1 x1 x
x2 x2 x
x N x N x

3.

3. Квадрат средней квадратичной погрешности:

4.

4. Вычисляем систематическую погрешность, вносимую прибором.
xсист
- Соответствует цене деления прибора
5. Полная (абсолютная) погрешность:
x S x
2
x
2
сист

5.

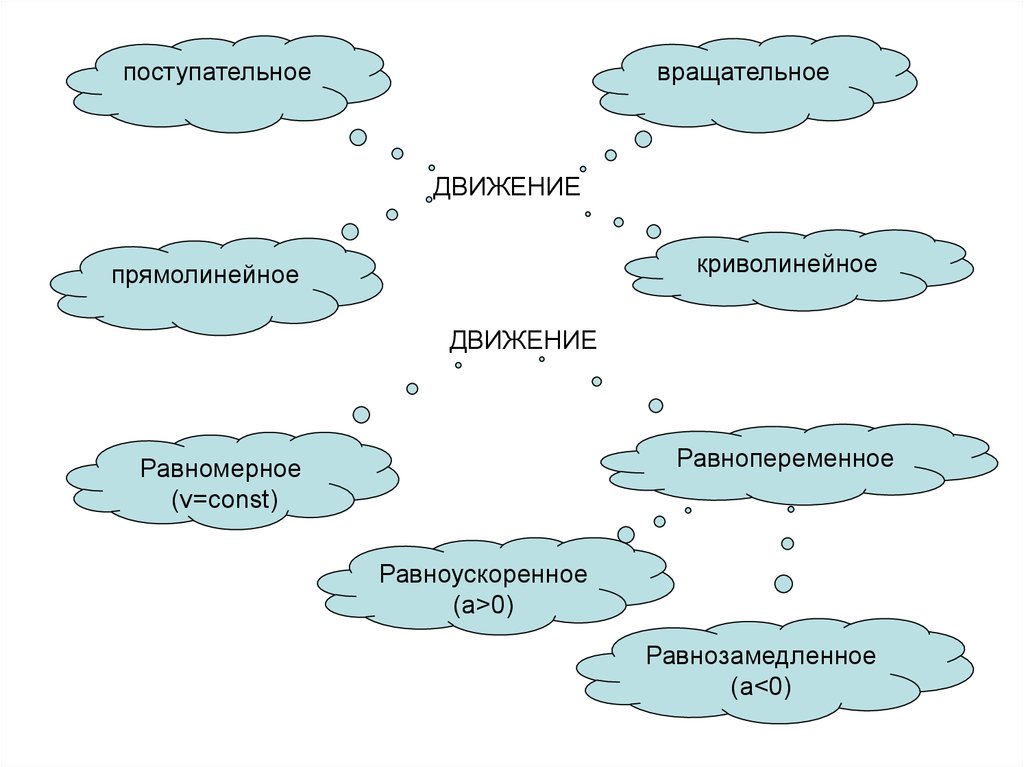
поступательное
вращательное
ДВИЖЕНИЕ
криволинейное
прямолинейное
ДВИЖЕНИЕ
Равнопеременное
Равномерное
(v=const)
Равноускоренное
(a>0)
Равнозамедленное
(a<0)

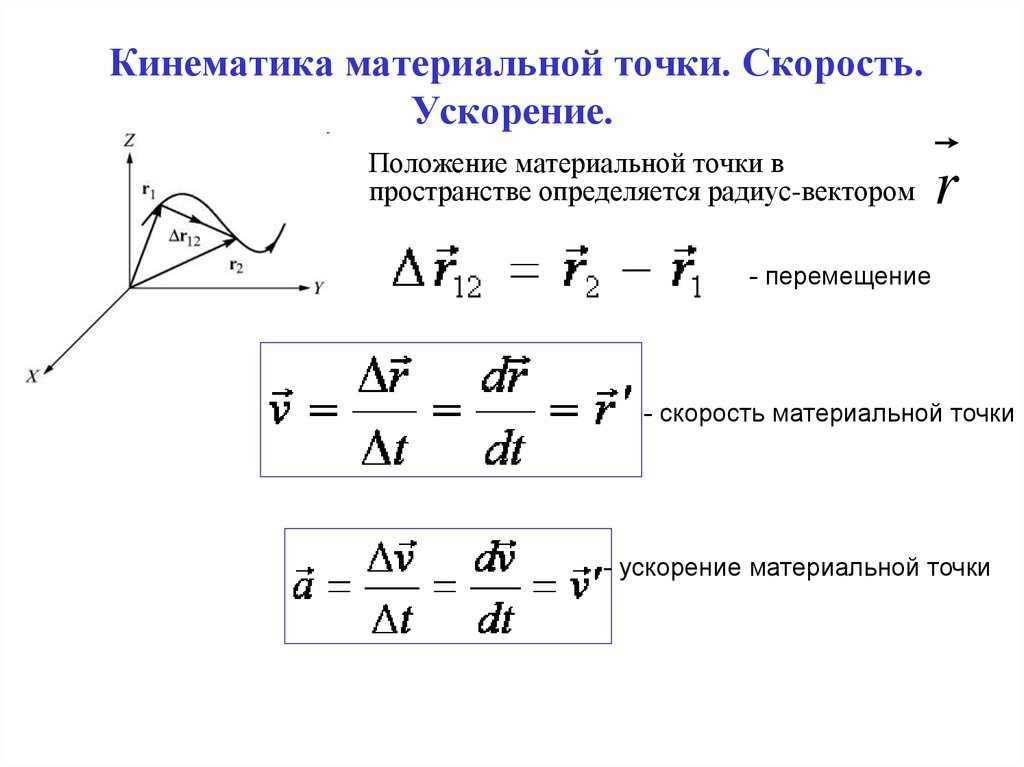
6. Кинематика материальной точки. Скорость. Ускорение.

Положение материальной точки в
пространстве определяется радиус-вектором
r
- перемещение
- скорость материальной точки
- ускорение материальной точки

7.

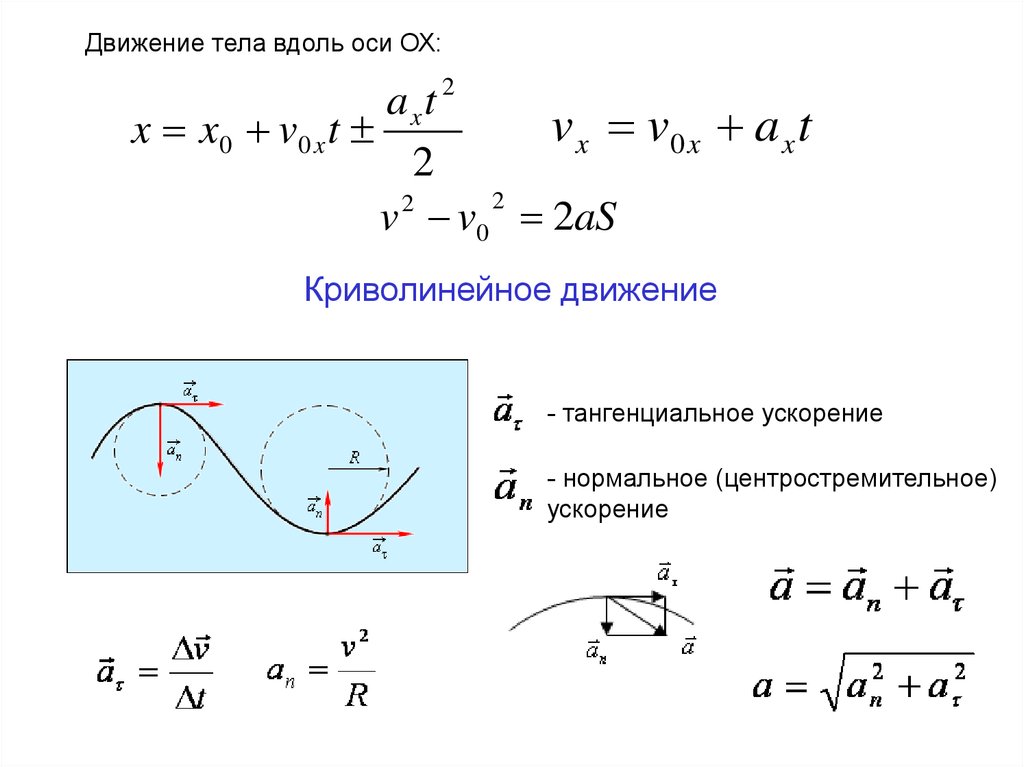
Движение тела вдоль оси ОХ:
2
axt
v x v0 x a x t
x x0 v0 x t
2
2
2
v v0 2aS
Криволинейное движение
- тангенциальное ускорение
- нормальное (центростремительное)
ускорение

8.

Вращательное движение
dφ – угол поворота (рад)
- угловая скорость (рад/с)
- угловое ускорение (рад/с2)
Период вращения – время, за которое материальная
точка совершает один полный оборот:
2
T
Обратная периоду величина называется
частотой вращения
1
T 2
Циклическая частота:
2

9.

Параметры вращательного движения можно связать с
параметрами поступательного движения:
v R
a R
an R
2

10.

Задача 1.
Решение:
S
t
t 0 1 c : S 5 м
5
5м / с
1
t 1 3 c : S 0
5
t 3 5 c : S 10 5 5 м 2,5 м / с
2
15
t 5 7 c : S 25 10 15 м
7,5 м / с
2
Ответ : t 0 1 c.

11.

Задача 2.
Решение:
a
t
5
0,5 м / с 2
10
15
t 10 20 c : 20 5 15 м / c a
1,5 м / с 2
10
20
t 20 30 c : 0 20 20 м / c a
2 м / с 2
10
10
t 30 40 c : 10 0 10 м / c a
1м / с 2
10
t 0 10 c : 5 0 5 м / c a
Ответ : t 20 30 c.

12.

Задача 3.
Решение:
x 2 2 0,5 2 3 0
dx
x
dt
2 t 0,5t
a
3
1 0,5 3t
2
1 1,5t 2 1 1,5 2 2 1 6 5 м / с.
d
dt
a 1 1,5t
2
3t 3 2 6 м / с
2
Ответ :х 0, м / с, а -6 м/с 2 .

13.

Задача 4.
Решение:
Дано:
4 2t 3t 2 м / с
t
t 3c
S ?
S dt
0
3
S
0
3
2t
3t
2
3
4
3
3
3
48 м
4
t
4 2t 3t dt
2
3 0
2
2
3
Ответ: 48 м.

14.

Задача 5.
Решение:
Дано:
a 5 4t 6t 2 м / с
t 2c
?
0
adt
0
2
4t
6t
5 2 2 2 2 2 23 2 м / с
5 4t 6t dt 5t
2
3 0
2
t
2
2
3
Ответ: 2 м/с.

15.

Задача 6.
Дано:
Решение:
S 0,4t 0,1t
t 1c
R 3м
a n ? a ?
a ?
2
an
d
dt
a
dS
0,8t 0,1 м / с
dt
d
an
0,8 м / с 2
dt
0,9 2
2
a
0
,
27
м
/
с
(t 1c) 0,9 м / с
R
3
a an a 0,84 м / с 2
2
2
R

16.

Задача 7.
Дано:
Решение:
10 20t 2t 2 рад
a r
r 0,1 м
t 4 c
a ?
an r
2
a 2r 2 4r 2 r 2 4
d
10 20t 2t 2 20 4t
dt
d
20 4t 4 рад / с 2
dt
(t 4c) 20 16 4 рад / с
a 0,1 4 2 ( 4) 2 1,65 м / с 2

17. Законы в механике

18.

Первый закон Ньютона
Существуют системы отсчета, называемые
инерциальными, в которых при отсутствии воздействия
других тел частица сохраняет стационарное состояние
движения: движется равномерно и прямолинейно (в
частном случае - покоится).
Второй закон Ньютона
Сила, действующая на тело, равна
произведению массы тела на
сообщаемое этой силой ускорение
Третий закон Ньютона
Силы, с которыми две материальные точки
воздействуют друг на друга, всегда равны по модулю
и направлены в противоположные стороны вдоль
прямой, соединяющей эти точки

19.

Законы сил в механике
Сила гравитационного притяжения, действующая между двумя
материальными точками, пропорциональна произведению масс точек и
обратно пропорциональна квадрату расстояния r между ними и
направлена вдоль прямой, соединяющей эти точки, от одного тела к
другому:
Сила тяжести
Сила реакции опоры
(сила нормального давления)
Вес тела – это сила, с которой тело
вследствие его притяжения к Земле
действует на опору или подвес

20.

Упругая сила пропорциональна смещению материальной точки из
положения равновесия и направлена к положению равновесия
Fупр kх
Сила трения скольжения, возникающая при скольжении данного
тела по поверхности другого тела
Fтр N

21.

Пример.
Поезд массой 1000 т на пути 500 м увеличивает скорость от 36 км/ч
до 72 км/ч. Коэффициент сопротивления движению 0,005. Найти силу тяги
локомотива, считая её постоянной.
Дано:
Решение:

22.

23. Законы сохранения в механике

24.

25.

Закон сохранения импульса.
В замкнутой системе векторная сумма импульсов всех
тел, входящих в систему, остается постоянной при
любых взаимодействиях тел этой системы между собой.

26.

Импульс силы – физическая векторная величина, равная произведению
силы на время ее действия:
При стрельбе из орудия возникает отдача – снаряд движется вперед, а
орудие – откатывается назад. Снаряд и орудие – два
взаимодействующих тела. Скорость, которую приобретает орудие при
отдаче, зависит только от скорости снаряда и отношения масс.

27.

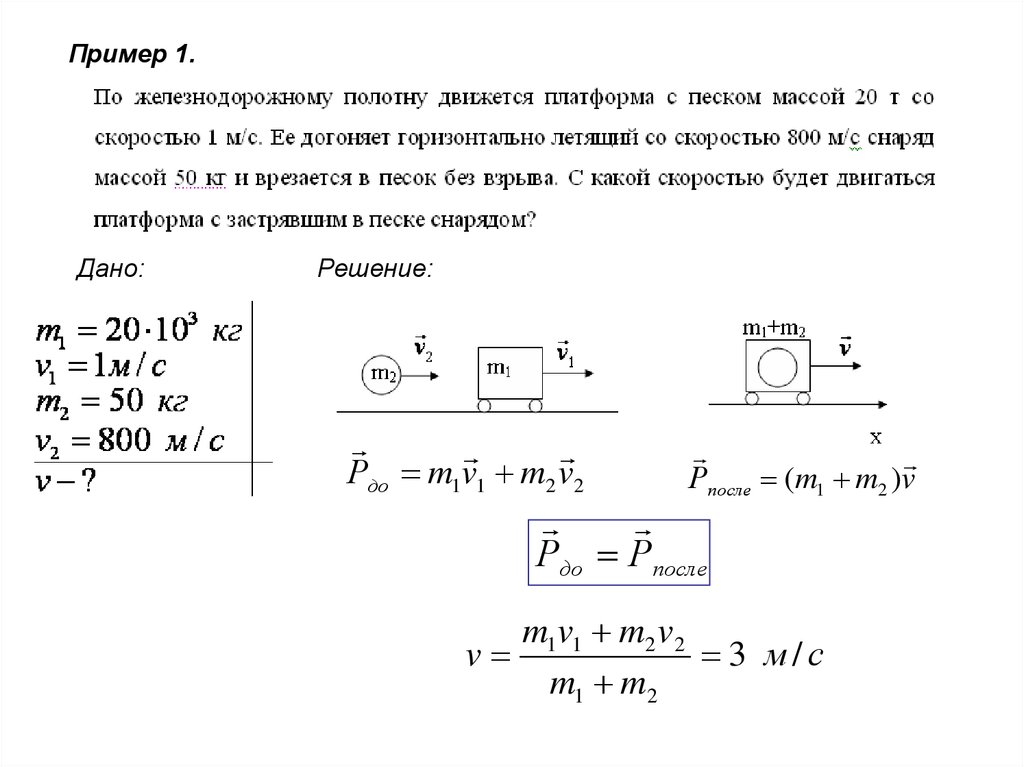
Пример 1.
Дано:
Решение:
Рдо m1v1 m2 v2
Рпосле (m1 m2 )v
Рдо Рпосле
m1v1 m2 v2
v
3 м/с
m1 m2

28.

Пример 2.
Дано:
Решение:
Рдо m1v1 m2 v2
Рдо Рпосле
OX : Рдо m1v1 m2 v2
Рпосле (m1 m2 )v
OX : Рпосле (m1 m2 )v
m1v1 m2 v2 2
v
м/с
m1 m2
7

29.

Закон сохранения механической энергии
Полная механическая энергия:
Кинетическая энергия:
Е Еп Ек
mv 2
Ек
2
Потенциальная энергия в поле силы тяжести Земли:
Потенциальная энергия в поле упругих сил:
Еп
Еп mgH
kx2
2
Если в замкнутой системе не действуют силы,
трения и силы сопротивления, то сумма
кинетической и потенциальной энергии всех тел
системы остается величиной постоянной.
Е Еп Ек const

30.

Пример 1.
Тело массы m падает свободно на землю с высоты H
без начальной скорости.
Е Еп Ек const
Е1 Еп1 Ек1
E E E
Е п1 mgH , Е к1 0
Е2 Еп 2 Ек 2
Е п 2 mgh, Е к 2
mv2
2
Е3 Е п 3 Е к 3
Е п 3 0, Е к 3
mv3
2
2
2
Е1 mgH
mv2
Е 2 mgh
2
mv3
Е3
2
1
2
2
3
2

31.

Пример 2.
Пружина жесткостью k растянута так, что её деформация
равна xmax.
2
mvmax
Е1
2
1
kx 2 mv 2
Е2
2
2
2
3
2
kxmax
Е3
2
E1 E2 E3

32.

Пример 3.
Автомобиль, двигаясь с выключенным двигателем, на горизонтальном участке
дороги имеет скорость 20 м/с. На какую высоту он поднимется до полной остановки
вверх по склону горы под углом 30° к горизонту? Трением пренебречь.
У основания наклонной плоскости:
В момент остановки:
mv 2
Е полная Е к
2
Еполная Еп mgH
mv 2
mgH
2
H 20 м
Пример 4.
На рисунке представлена траектория движения
тела, брошенного под углом к горизонту. В какой из
четырех точек, отмеченных на траектории,
потенциальная энергия тела имеет минимальное
значение?
Ответ: 4

33.

Пример 5.
По какой из формул можно определить кинетическую энергию Ек, которую
имеет тело в верхней точке траектории?
В начальный момент времени:
В верхней точке траектории:
mv02
E полная
mgh
2
Еполная Ek mgH
mv02
Ek
mgh mgH
2

34.

Работа силы
A FS FS cos
Теорема о кинетической энергии: изменение кинетической энергии
тела (материальной точки)за некоторый промежуток времени
равно работе, совершенной силой, действующей на тело, за этот
же промежуток времени

35.

Работа равна убыли потенциальной энергии:
А Еп1 Еп 2 Еп

36.

37.

Динамика вращательного
движения твердого тела

38.

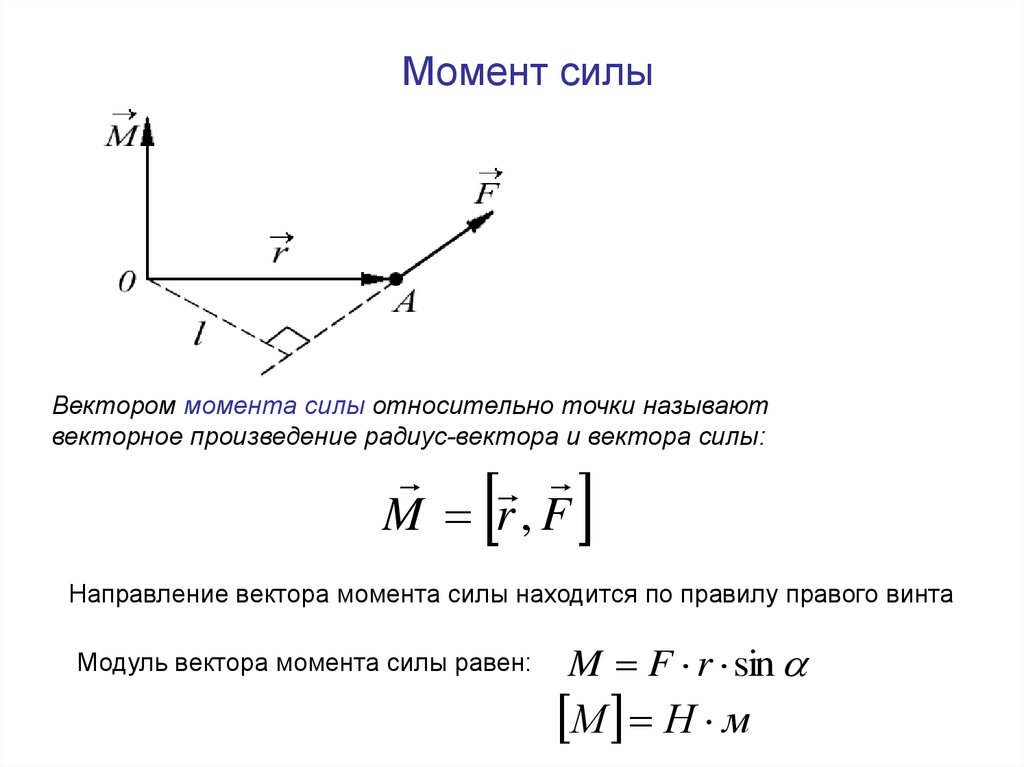
Момент силы
Вектором момента силы относительно точки называют
векторное произведение радиус-вектора и вектора силы:
M r, F
Направление вектора момента силы находится по правилу правого винта
Модуль вектора момента силы равен:
M F r sin
М Н м

39.

40.

Момент импульса
Вектором момента импульса м.т. относительно точки О
называют векторное произведение радиус-вектора и вектора
импульса относительно этой же точки:
L r, P
Направление вектора момента импульса находится по правилу правого
винта и совпадает с вектором угловой скорости.
Модуль вектора момента импульса равен:
L P r sin
L кг м
2
/c

41.

Момент инерции
Момент инерции — скалярная физическая величина, мера инертности во
вращательном движении вокруг оси, подобно тому, как масса тела является
мерой его инертности в поступательном движении.
Характеризуется распределением масс в теле: момент инерции равен сумме
произведений элементарных масс на квадрат их расстояний до базового
множества (точки, прямой или плоскости).
I mi ri
2
I r dm
2
I кг м 2

42.

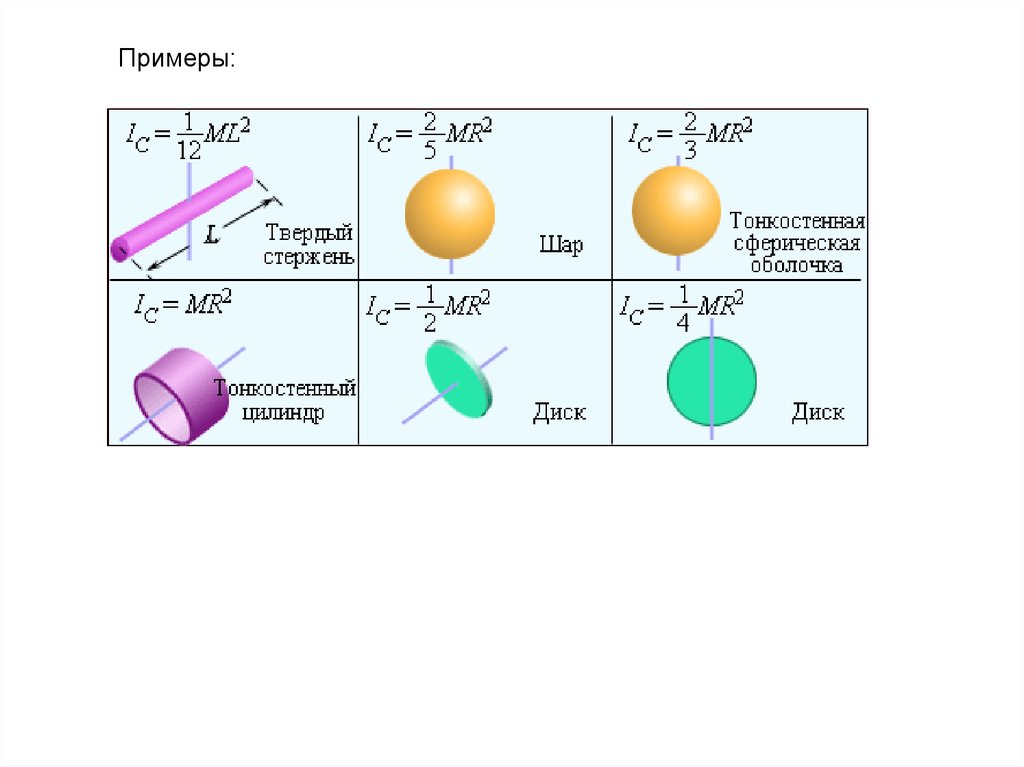
Примеры:

43.

Теорема Штейнера
Момент инерции абсолютно твердого тела
I относительно произвольной оси вращения Z
равен сумме момента инерции этого тела Ic
относительно воображаемой оси, проходящей
через
центр
масс
тела
параллельно
рассматриваемой оси, и произведения
массы тела m на квадрат расстояния a между
этими осями:
I I c ma
2

44.

Уравнение моментов
M r, F
dp
Fв неш.
dt
L I
dp d
dL
M r , r , p
dt dt
dt
dL
M
dt
M I
- Уравнение моментов
- Основное уравнение
динамики вращательного
движения

45.

Работа при вращательном движении твердого тела.

46.

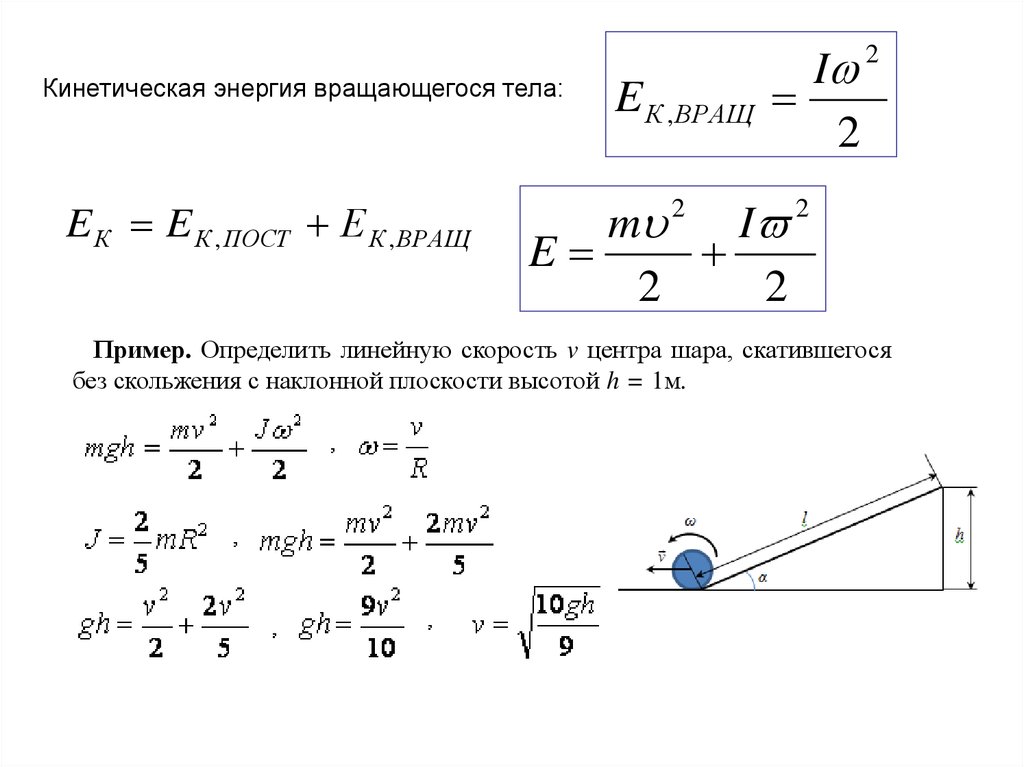
Кинетическая энергия вращающегося тела:
E К E К , ПОСТ Е К , ВРАЩ
E К , ВРАЩ
I 2
2
m 2 I 2
E
2
2
Пример. Определить линейную скорость v центра шара, скатившегося
без скольжения с наклонной плоскости высотой h = 1м.

47.

Кинетическая энергия вращающегося тела:
E К E К , ПОСТ Е К , ВРАЩ
E К , ВРАЩ
I 2
2
mv
I
E
2
2
2
2

48.

Закон сохранения момента импульса
Момент импульса замкнутой системы тел относительно любой
неподвижной точки не изменяется с течением времени:
L const
L I
I1 1 I1 I 2