Электромагнитные взаимодействия заряженных частиц

1. Международный государственный экологический институт им.А.Д.Сахарова БГУ

ФИЗИКА ЯДРА и ИИ
1-31 04 05 Медицинская физика
Тема Электромагнитные взаимодействия заряженных частиц
2020 – 2021 учебный год

2. Электромагнитные взаимодействия заряженных частиц

Электромагнитные взаимодействия существуют между всеми частицами, имеющими
электрический заряд, и фотонами. Их можно рассматривать как результат обмена
фотонами в момент взаимодействия или как результат поглощения и испускания
фотонов. В качестве константы взаимодействия, определяющей интенсивность
процесса, в случае электромагнитных взаимодействий выступает квадрат заряда e2 или
безразмерная величина, пропорциональная e2:
α = e2/ħс = 1/137.
Если в процессе взаимодействия участвует один фотон, то вероятность такого
процесса пропорциональна α, если два фотона, то пропорциональна α2 и т.д.
Рассмотрим основные процессы, которые происходят с наибольшей вероятностью и
при которых осуществляется наибольшая передача анергии. Эти элементарные
электромагнитные процессы можно классифицировать с точки зрения классической
физики на основе представления о параметре удара (прицельном параметре
соударений) b, т.е. расстоянии наибольшего сближения частиц.

3. Электромагнитные взаимодействия заряженных частиц

• При взаимодействии частиц с атомами среды, через которую
они летят, естественно сопоставлять величину параметра
удара b с размерами атомов a.
• В зависимости от того, как соотносятся между собой величины
b и a происходит тот или иной процесс взаимодействия:
• b >> α Если параметр удара настолько велик, что атом реагирует как
целое на переменное электромагнитное поле, создаваемое
заряженной частицей, то возникает возбуждение и ионизация
атомов. Взаимодействие фотона с атомом, как целым, приводит к
фотоэффекту.

4. Электромагнитные взаимодействия заряженных частиц

• b ~ α Если параметр удара сравним с размерами атома, то будет происходить
взаимодействие частицы с отдельными электронами атома. В этом случае
заряженная частица может передать электрону значительную энергию,
электрон вырывается из атома и сам может производить ионизацию других
атомов. Такой электрон называется δ-электроном.
• Если энергия, получаемая δ-электроном, велика по сравнению с энергией
связи в атоме, то зто явление может рассматриваться как взаимодействие
пролетающей частицы и свободного электрона. При столкновении фотона с
таким "свободным" электроном фотон рассеивается (комптоновокое
рассеяние, комптон-эффект).
• b << α При еще меньших значениях параметра удара происходит
взаимодействие частицы с кулоновским полем ядра. Траектория частицы при
этом заметно искривляетcя, и происходит ускорение (или замедление) частицы.
Согласно классической электродинамике в этом случае должно возникнуть
тормозное излучение.

5. Электромагнитные взаимодействия заряженных частиц

• При взаимодействии фотонов высокой энергии с ядрами атомов
могут возникать электрон-позитронные пары. При этом фотон
поглощается, и вся его энергия переходит в энергию пары.
• Этот эффект пороговый, так как он может происходить, если энергия
фотона больше суммарной энергии покоя электрона и позитрона
hν > 2mec2.
• Ядро принимает на себя избыток импульса. Заряженные частицы
тоже могут образовывать электрон-позитронные пары e− e+, так как
электромагнитное поле быстро движущейся частицы может быть
представлено как поток фотонов со спектром, зависящим от энергии
частицы. Эти виртуальные фотоны могут создавать e−e+-пары так же,
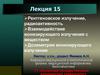
как и реальные фотоны. Схематически прямое рождение e−e+-пары
электроном изображено на слайде.

6. Прямое рождение e−e+-пары электроном. Виртуальный фотон на опыте не наблюдается.

7. Процессы излучения электромагнитных волн

• Особый класс взаимодействий составляют процессы излучения
электромагнитных волн при равномерном движении частиц в среде с
показателем преломления n > 1.
• К ним относится излучение Вавилова-Черенкова, на основе которого
созданы разнообразные черенковские детекторы. Кроме того, есть
переходное излучение, возникающее при переходе частицы через
границу раздела двух сред с различными диэлектрическими
постоянными.
• Излучение Вавилова-Черенкова - свечение, вызываемое в
прозрачной среде заряженной частицей, движущейся со скоростью,
превышающей фазовую скорость распространения света в этой
среде.

8. Излучение Вавилова — Черенкова в охлаждающей жидкости исследовательского реактора ATR  Национальной лаборатории Айдахо

Излучение Вавилова — Черенкова в охлаждающей
жидкости исследовательского реактора ATR Национальной
лаборатории Айдахо

9. Размер атома

• Пусть имеем ядро с зарядом Ze.
• Рассмотрим электрон в стационарном
состоянии, т.е. допустим, что электрон
вращается вокруг ядра по стационарной
круговой орбите радиуса a с орбитальной
скоростью vорб.
• Атом - система квантовая, поэтому момент
количества движения me·vорб · квантуется, т.е.
может принимать лишь дискретные значения
me·vорб·a = nħ, где n = 1,2,3,….
Стационарная
круговая
орбита электрона в
атоме

10.

• Поскольку рассматриваемая система стационарна, то центробежная сила
равна кулоновской силе притяжения электрона к ядру, т.е.
• me v орб 2/a = Z e2 /а2 ;
• Z e2 = me v орб 2 a ;
• n v орб = Z e2;
• Отсюда получаем важные для нас соотношения:
• v орб = Z e2/ n ħ,
• а = n ħ / me v орб = n2 ħ2/ me Z e2.

11.

• т.е. скорость вращения электронов в атоме убывает с увеличением главного
квантового числа n, а радиус орбиты вращения электронов в атоме
пропорционален n2.
• Энергия связи электрона с ядром (Eсв), т.е. его потенциальная энергия на
орбите, получается равной:
• Eсв = Z e2/a = me v орб 2;
• v орб 2; = Eсв /me.
• Энергия связи электрона с ядром (Eсв), т.е. его потенциальная энергия
на орбите, получается равной:
• Eсв = Z e2/a = me v орб 2;
• v орб 2; = Eсв /me.
• Отсюда видно, что скорость вращения больше у внутренних электронов
атома, для которых больше Eсв.

12.

• Например, для К-электронов n = 1, следовательно
• vорб = Ze2/ћ
Для атома водорода Z = 1, поэтому
vорб = e2/ћ = 2.3·108 см/с и
a = ћ2/mee2 = 0.5·10-8 см.
В общем случае для электронных орбит в атомах имеем:
• vорб = Z/n · 2.3·108 см/с и
• a = n2/Z · 5·10-7 см.

13. Условие ионизации

• Чтобы произошла ионизация, т.е. электрон мог покинуть атом, надо чтобы
при взаимодействии с пролетающей мимо заряженной частицей этот
электрон получил кинетическую энергию Ee большую, чем энергия связи его
с атомом Eсв, т.е. Ee > Eсв.
• Определим минимальную кинетическую энергию и скорость v пролетающей
частицы, необходимую для ионизации ею атома среды. Пусть пролетающая
частица имеет массу M >> me и кинетическую энергию E = Mv2/2.
• Так как максимальная энергия, которая может быть передана при упругом
столкновении
• Емах = [4 me М / (М + me )2] E.
• При М > > me Ее ~ Е me /М
• Чтобы электрон смог покинуть этот атом, необходимо, чтобы Ee > Eсв, т.е.
me/M · E > Eсв. Отсюда получаем соотношения
• E/M = Eсв/me и v > 2vорб.

14. Условие ионизации

Если энергия, передаваемая электрону Ee>>Eсв, т.е. энергия
пролетающей частицы Ее > Есв М /me , то все электроны атома могут
рассматриваться свободными и покоящимися по сравнению с
быстролетящей частицей.
• Какова же должна быть энергия частицы, чтобы выполнялось это
условие?
Найдем, например, энергию протона, который имеет скорость v =
4.6·108см/с (т.е. равную 2vорб для атома водорода):
• Ер = М v2 /2 = 1/2 Mc2 (v/c)2 =100 кэВ.
• Протон с Ep > 100 кэВ может ионизовать атом водорода, но лишь при
энергии протона Ep >> 100 кэВ можно пренебречь связью электронов
с ядрами атомов водорода и считать их свободными.

15. Ионизационные потери тяжелых заряженных частиц

• Ионизация вещества − явление исключительное по своему значению для
экспериментальной ядерной физики и физики высоких энергий, поскольку
оно лежит в основе действия большинства детекторов элементарных частиц.
• Путем регистрации ионизации были открыты естественная радиоактивнооть и
космические лучи, впервые наблюдались реакции расщепления атомных
ядер.
• В результате возбуждения и ионизации быстрыми заряженными частицами
атомов вещества детектора и последующего усиления слабого
первоначального ионизационного сигнала возникает наблюдаемый
макроскопический ионизационный эффект. Измерения этого ионизационного
эффекта как и времени пролета, а также черенковского излучения широко
используются для идентификации заряженных частиц и интерпретации
экспериментов.

16. Ионизационные потери тяжелых заряженных частиц

• Основные закономерности, описывающие ионизационные потери
тяжелых заряженных частиц, можно получить из сравнительно
простых качественных соображений, основанных на классических
представлениях. Впервые эти закономерности были получены в
1915 г. Нильсом Бором.
• Рассмотрим прохождение через вещество тяжелой (M >> me)
нерелятивистской (V << c) заряженной (ze) частицы.
• Предположим, что частица эта настолько быстрая (V >> vорб), что
можно считать все атомные электроны свободными.

17. Ионизационные потери тяжелых заряженных частиц

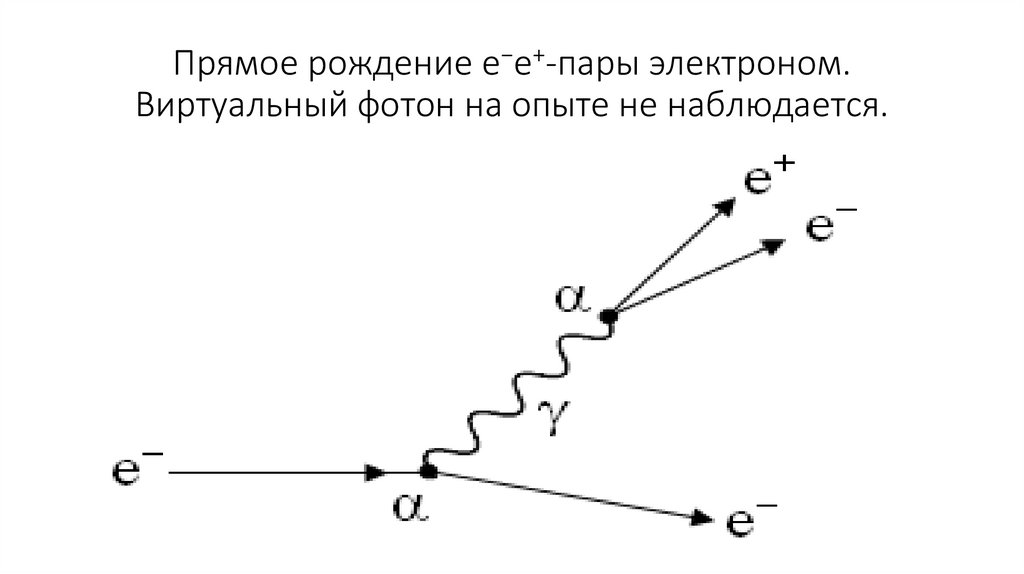
• Сначала разберем взаимодействие этой частицы с одним электроном
среды, расположенным на расстоянии b от ее траектории (b −
прицельный параметр) (рис.).
• В результате электростатического взаимодействия электрон получает
импульс в направлении, перпендикулярном к направлению движения
частицы. Продольная же составляющая импульса электрона близка к
нулю, так как две ее компоненты, соответствующие приближению
частицы к электрону и удалению от него, почти равны по величине
(если потери энергии частицей малы) и противоположны по
направлению.
• Так как M >> me, то можно не учитывать изменения направления
движения частицы после такого единичного взаимодействия

18. Взаимодействие заряженной частицы с электроном атома

E/M > Eсв/me и v > 2vорб.
1.Итак, в результате действия кулоновских сил между частицей и электроном
среды этот электрон получает импульс pe = F · t

19. Взаимодействие заряженной частицы с электроном атома

• Итак, в результате действия кулоновских сил между частицей и
электроном среды этот электрон получает импульс pe = F · t, где
• F = ze e/b2; t = 2b /c – время взаимодействия т.е.
• Ре = z e2 / b2 2b/v = 2 z e2 /(vb).
• Если электрон в результате взаимодействия приобрел импульс
2 z e2 /(vb), то, следовательно, он приобрел и кинетическую энергию:
• Te = p e 2/(2me ) = 2 z2 e4/ (v2 b2 me )
• Вспоминаем закон сохранения энергии для данного частного случая:
сколько энергии приобрел электрон (Te), столько же энергии (∆E)
потеряла частица при взаимодействии с этим электроном:
• ‫∆׀‬E‫ = ׀‬Te = 2 z2 e4/ (v2 b2 me )

20. Взаимодействие заряженной частицы с электроном атома

• Теперь вспомним, что среда наполнена атомами (A,Z) и,
следовательно, в ней много электронов. Если плотность среды ρ г/см3,
то плотность атомов в ней будет:
• n at = ρ NA /A, (ат/см3)
• где NA − числе Авогадро. Плотность электронов будет в Z раз больше
• Ne = Z n at = (Z/A) ρ NA (ат/см3)
• Если частица проходит в среде путь dx, то она взаимодействует почти
одинаково со всеми электронами, которые располагаются на одном и
том же расстоянии b от ее траектории и каждому из них передает
энергию Te.

21. Взаимодействие заряженной частицы с электроном атома

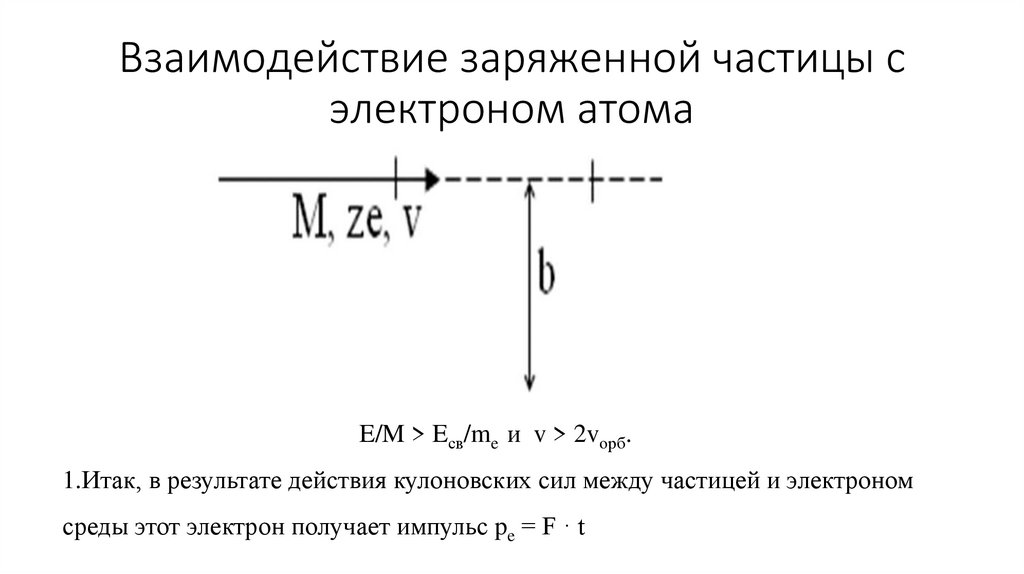
• Количество таких электронов на пути dx будет
определяться плотностью электронов и объемом
кольцевого цилиндра длиной dx с внутренним радиусом
b и внешним радиусом b + db (слайд).
• Объем этого цилиндра − 2πbdbdx (см3).
• Электронов в нем будет:
• ne(эл/см3) · 2πbdbdx (см3) = 2πbdbdx Znат.

22. К расчету ионизационных потерь

23. Взаимодействие заряженной частицы с электроном атома

• Каждому из этих электронов пролетающая частица передает энергию ∆E, а всем электронам,
находящимся на расстоянии b от нее на пути dx, частица передает энергию
• ‫∆׀‬E(b)‫׀‬
= 2 z2 e4/ (v2 b2 me ) nat 2π b db dx
• ‫∆׀‬E(b)/dx‫׀‬
= 4π e4 /me z2 / (v2 nat ) b2 ) Z db/b.
• He следует забывать, что энергия частицы при этом взаимодействии уменьшается, и поэтому
производная dE(b)/dx отрицательна.
• Чтобы найти ионизационные потери частицы на пути dx со всеми электронами среды, с
которыми она взаимодействует с разными параметрами удара, надо проинтегрировать по
всем возможным параметрам удара от bmin до bmax:
bmax
∆E(b)/dx‫ = ׀‬4π e4 /me z2 / v2 e nat Z) ∫ db/b.
bmin

24. Взаимодействие заряженной частицы с электроном атома

• Минимальному значению параметра удара bmin соответствует
максимальная передаваемая энергия.
• Чем больше параметр удара, тем меньше передаваемая
электрону энергия. Максимальное значение (bmax) соответствует
случаю, когда передаваемая энергия близка к энергии связи этого
электрона с ядром.
• Поскольку энергия связи разных электронов атома различна, то
вводится обычно некоторая усредненная характеристика энергии
связи электронов в атомах данного элемента (A,Z), называемая
средним потенциалом ионизации I.
• Для разных элементов I = I0 · Z, где I0 слабо зависит от Z вещества.

25. Величины I0 для разных элементов

Величины I0 для разных элементов
Вещество
Be
C
Воздух
Al
Cu
Pb
I0, эВ
16.0
13.0
12.8
12.8
11.1
10.0

26. Взаимодействие заряженной частицы с электроном атома

• Итак, выбираем в качестве максимального прицельного
параметра такой, при котором электрону передается энергия,
равная среднему потенциалу ионизации. Так как
• bmax 2 = 2 z2 e4/me v2 1/ I;
• Ln(bmax/bmin) = 1/2 (bmax 2/bmin 2)
• Подставляя найденные нами значения bmax и bmin, получаем:
• Ln(bmax/bmin) = 1/2 ln(2me v2/ I(1-β2)
• Вывод этой формулы на основе классических представлений
первоначально был предложен Н. Бором в 1915 г., поэтому она и
называется формулой Бора в этом виде или в более уточненном
варианте:

27. Взаимодействие заряженной частицы с электроном атома

Формула Бора
-dE/dx = 4πe2/me *Z2/v2 *nat Z * {ln [Z me v2 /[I (1 – β)] – β2 - δ – u} эрг/см-1.
Зависимость ионизационных потерь от параметров частицы
1. Удельные ионизационные потери пропорциональны квадрату заряда
частицы:|dE/dx| ~ z2.
• Это означает, что удельные ионизационные потери ядра железа (z = 26) в 676
раз больше, чем для протона той же скорости.
• 2. Удельные потери не зависят от массы частицы М. Это получается из-за того,
что происходит взаимодействие электрических зарядов частиц, а не их масс.
Однако, если интересоваться сопоставлением потерь на ионизацию различных
частиц с одинаковой кинетической энергией, тогда в коэффициент перед
логарифмическим членом неизбежно войдет масса частицы, так как v2 ~ E/M.

28. Взаимодействие заряженной частицы с электроном атома

• Поскольку в нерелятивистском случае ионизационные потери обратно
пропорциональны квадрату скорости частицы:
• |dE/dx| ~ 1/v2, | dE/dx| ~ M/E.
• Следовательно, частицы с одинаковой кинетической энергией теряют ее на
ионизацию тем больше, чем больше их масса. Например, дейтрон теряет на
единице своего пути на ионизацию энергию в 2 раза большую, чем протон с
такой же кинетической энергией, а мюон в ~9 раз меньше.
• 3. Удельные потери энергии на единице пути |dE/dx| являются довольно
сложной функцией скорости (и, следовательно, кинетической энергии)
частицы. Эта зависимость схематически изображена на рис., где по оси
абсцисс отложена кинетическая энергия в единицах своей собственной
энергии Mc2, а по оси ординат − удельные потери энергии этой частицей на
ионизацию среды.

29. Зависимость ионизационных потерь энергии от энергии тяжелых частиц

30. Ионизационные потери тяжелых частиц

• ВС Участок (ВС) соответствует случаю, когда, с одной стороны, частица
нерелятивистская, таким образом Eкин < Mc2 и β < 1, с другой стороны, она
настолько быстрая, что все электроны атомов могут считаться свободными.
Поведение кривой в этой области (ВС) определяется коэффициентом перед
квадратными скобками в формуле Бете-Блоха:
• ‫׀‬dE/dx ‫ = ~ ׀‬4πe4/me *z2/v2 *nat Z, т.е dE/dx ‫ ~ ׀‬1/Е
• Эта зависимость в нерелятивистской области получилась из-за того, что
переданный электрону импульс pe = F · t зависит от времени взаимодействия t,
которое, в свою очередь, обратно пропорционально скорости частицы t ~ 1/V.
• Переданная же электрону энергия ~ Pe2 т.е. энергия, потерянная частицей ~ 1/v2,
следовательно ~ 1/E.
• Зависимость |dE/dx| ~ 1/v2 имеет место вплоть до релятивистских скоростей V ≈
c. При V ≈ c коэффициент перед скобкой принимает минимальное значение.

31. Ионизационные потери тяжелых частиц

• СD На участке (СD) кривой на рис. удельные ионизационные потери
снова начинают увеличиваться. Этот рост потерь обусловлен ростом
величины логарифмического члена, так как при β → 1 1/(1 − β2) → ∞.
Поскольку этот множитель стоит под знаком логарифма, то и рост
потерь наблюдается медленный - "логарифмический".
Логарифмическое возрастание dE/dx с увеличением энергии обычно
называют релятивистским подъемом ионизации. Он начинается после
того, как dE/dx достигнет минимальной величины при V ≈ 0.96c.
Частично этот подъем происходит за счет близких столкновений, так как
увеличивается максимальная передаваемая энергия ∆Emax, а частично за
счет далеких столкновений из-за релятивистского увеличения bmax

32. Ионизационные потери тяжелых частиц

• Рост потерь, обусловленный вторым фактором, происходит из-за
релятивистского сжатия кулоновского поля частицы в продольном
направлении (вдоль траектории частицы) и возрастания поля в
поперечном направлении.
• Слайд иллюстрирует сказанное: для нерелятивистских частиц
эквипотенциальная поверхность имеет сферически симметричную
форму (а), а форма эквипотенциальной поверхности поля
релятивистских частиц другая (б):
• расстояние в продольном направлении уменьшается в (1 − β2)1/2 раз, а
в поперечном − увеличивается в (1 − β2)-1/2 раз, получается эллипсоид,
"блин", который с увеличением скорости частицы все более
сплющивается в продольном направлении и увеличивается в
поперечном.

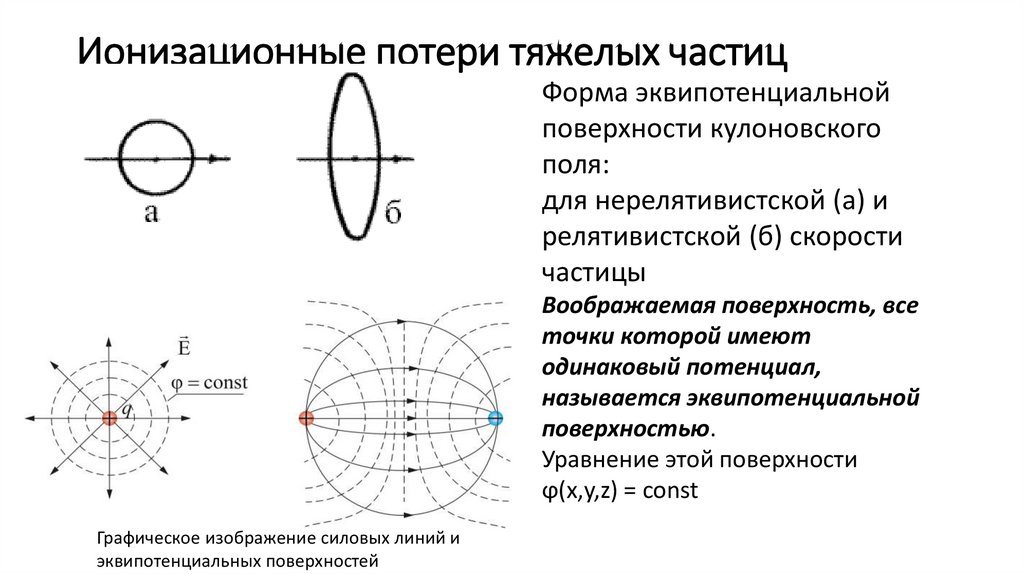
33. Ионизационные потери тяжелых частиц

Форма эквипотенциальной
поверхности кулоновского
поля:
для нерелятивистской (а) и
релятивистской (б) скорости
частицы
Воображаемая поверхность, все
точки которой имеют
одинаковый потенциал,
называется эквипотенциальной
поверхностью.
Уравнение этой поверхности
ϕ(x,y,z) = const
Графическое изображение силовых линий и
эквипотенциальных поверхностей

34. Ионизационные потери тяжелых частиц

• Это означает, что все большее число электронов среды попадает в поле воздействия
летящей частицы. Растет bmax и все большему числу электронов частица передает
свою энергию. Следовательно, и потери энергии частицей на единице ее пути растут.
Казалось бы, эффект релятивистского сжатия поля должен был бы приводить к
неограниченному увеличению потерь. Однако это не так. При дальнейшем
увеличении энергии поле частицы может стать больше расстояния между атомами
среды. В этом случае возникает так называемый эффект плотности, который
особенно существенен для плотных газов, жидкостей и, тем более, для твердых
веществ.
• Эффект плотности связан с тем, что поле летящей частицы поляризует атомы среды. В
результате поляризации многих атомов возникает поле диполей, направленное в
сторону, противоположную полю летящей частицы. Оно ослабляет поле частицы и
как бы экранирует от него далеко расположенные электроны. На некотором
расстоянии от траектории частицы поле ее компенсируется полностью
противоположным полем диполей.

35. Ионизационные потери тяжелых частиц

• EF Область кривой (EF) и соответствует этому случаю: рост потерь
энергии существенно замедляется из-за эффекта плотности.
В формуле Бете-Блоха эффект плотности учитывается членом "δ".
Поскольку поляризация прямо пропорциональна плотности электронов
в среде (ne), то этот эффект в сильной степени зависит от плотности
вещества,
за
что
и
получил
свое
название.
Поправка на эффект плотности в несколько упрощенном виде
впервые была рассчитана Э.Ферми в 1939 г. и поэтому область (EF) часто
называют "плато Ферми". В крайнем релятивистском случае поправка на
эффект плотности дается выражением:
• δ = -ln (1 – β2) – ϕ
• ϕ = ln (I2/h2 ν 2) + 1
• ν = (ne e 2/(π me) 1\2

36. Ионизационные потери тяжелых частиц

• В предельном случае очень больших энергий часть релятивистского
возрастания потерь полностью компенсируется эффектом плотноcти.
• Оставшаяся часть связана с передачей энергии при близких
столкновениях. В случае не очень больших энергий максимальная
передаваемая энергия ∆Emax растет как (1 - β2)-1.
• При очень высоких энергиях ∆Emax возрастает приблизительно как (1 β2)-1/2, т.е. релятивистский подъем сказывается в три раза меньше того,
что можно было ожидать без учета эффекта плотности.
• AB Формула для ионизационных потерь была выведена в
предположении, что все электроны атомов среды при взаимодействии
с частицей могут считаться свободными, т.е. выполняется условие:
• ΔEmax >> Eсв, и E >> M Eсв/m

37. Ионизационные потери тяжелых частиц

• По мере уменьшения энергии частицы это соотношение может оказаться
нарушенным. В первую очередь, это нарушение будет относиться к
наиболее сильно связанным электронам в атомах: K- и L-электронам.
• Когда скорость частицы станет меньше скорости орбитального движения Kэлектронов, передача энергии им станет невозможной, и, следовательно,
K-электроны должны быть выключены при вычислении плотности
электронов в среде, т.е. число их как бы уменьшится, и, соответственно,
потери энергии также уменьшатся.
• При дальнейшей уменьшении скорости частицы то же самое следует
отнести и к L-электроном, затем к М-электронам и т.д. Чем больше Z среды,
тем больше Eсв и тем выше граничная энергия частицы, при которой
следует учитывать этот эффект:
• ν гр ~ νорбк = Z e2/ ħ

38. Ионизационные потери тяжелых частиц

• Пример. Для K-электронов скорость орбитального движения
• νорбк = 2.3·108Z см/с.
• Граничная энергия для протонов и α-частиц получаетcя равной:
Ep = 2,76 10 -2 Z2, MeV,
Eα = 0,11 Z2, MeV
• Чем больше масса частицы, тем выше граничная энергия. Для частицы
массы М граничная энергия получается равной:
• E ≈ 2,9 10 -5 M c2 Z 2
• Уменьшение потерь энергии частицей при малых энергиях соответствует
левому "завалу" кривой ионизационных потерь (АВ), и в формуле Бете-Блоха
учитывается последним членом u в квадратных скобках.
• При рассмотрении ионизационного торможения тяжелых заряженных
частиц (ионов атомов) нужно учитывать явление перезарядки, связанное с
захватом частицей электронов среды и их потерей.

39. Граничная энергия для протонов и α-частиц

Вещество
Z
C
Al
Cu
6
13
29
Vк орб ,
см/с
1.3·109
2.9·109
6.4·109
Ергр, МэВ
0.9
4.2
21.0
Еαгр, МэВ
3.6
16.9
84.0

40. Ионизационные потери тяжелых частиц

Этот эффект становится существенным при скоростях частицы, сравнимых с
vорб (участок АВ).
1.Положение максимума кривой (В) определяется Eгрдля этой среды.
Как было найдено, Eгр ~ Z2 среды.
2.Удельные ионизационные потери энергии пропорциональны плотности
электронов в среде:
|dE/dx| ~ Znат = ne.
Но
ne эл/см3 = Znат = (NA/A)·ρ·Z = NA·(Z/A)·ρ,
где NA − число Авогадро,
Z, А − заряд и атомный вес среды,
ρ г/см3 − плотность среды.

41. Ионизационные потери тяжелых частиц

• Для легких веществ Z/A ~ 0.5. Следовательно, для этих сред
получается простая зависимость |dE/dx| ~ ρ г/см3.
• Это обстоятельство побудило ввести в обиход массовую
единицу длины xρ, размерность которой [xρ] − г/см2.
• Смысл массовой единицы длины очевиден:
• это такая высота столбика вещества с сечением 1 см2,
который весит x ρ г,
• иначе говоря, это давление, которое оказывает на площадь
в 1см столбик вещества высотою x ρ.

42. Ионизационные потери тяжелых частиц

• Поскольку Z/A ~ 0.5, a I(A,Z) слабо влияет на величину потерь, так как
входит под знаком логарифма, то оказывается, что при расчете на 1
г/см2 ионизационные потери во всех веществах приблизительно
одинаковы.
• Для иллюстрации сказанного в табл.4 приведены ионизационные
потери энергии однозарядных релятивистских частиц около минимума
кривой, где E ≈ (2-3) Mc2.
• Как видно из табл.4, зависимость от A и Z слабая, но все же заметная
из-за того, что отношение Z/A уменьшается с ростом А.
• Величина потенциала ионизации I(A,Z) уже обсуждалась нами ранее.
И хотя потенциал ионизации I(A,Z) входит под знаком логарифма и
слабо сказывается на величине ионизационных потерь, тем не менее
для аккуратных вычислений его надо обязательно учитывать.

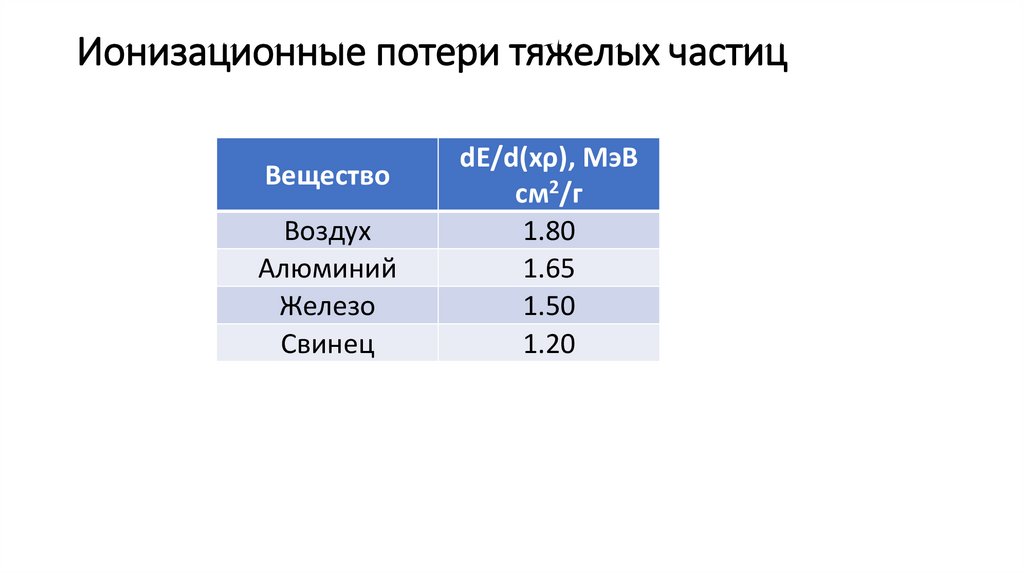
43. Ионизационные потери тяжелых частиц

Вещество
Воздух
Алюминий
Железо
Свинец
dE/d(xρ), МэВ
см2/г
1.80
1.65
1.50
1.20

44. Ионизационные потери электронов

45. Ионизационные потери тяжелых частиц

46.

• Наиболее надежным способом получения информации о сечении реакции
под эффективным действием моноэнергетических фотонов в настоящее время
признан метод «меченых» фотонов. В этом методе при продукты
фотоядерных реакций регистрируются на совпадение с рассеянными
электронами. Это позволяет определить энергию фотонов, вызывающих
реакцию: эти фотоны вырезаются («метятся») из сплошного спектра
тормозного γ излучения. Несмотря на очевидные принципиальные
преимущества, метод оказывается чрезвычайно сложным, а интенсивность
пучка моноэнергетических фотонов невысока. Как результат - количество
сечений реакций, измеренных с помощью этого метода в области энергий ГДР,
исчисляется единицами. В качестве источника моноэнергетических фотонов
регулируемой энергии в последнее время все более широко используется
также обратное комптон-рассеяние излучения мощного лазера на
движущемся электроне. В этом случае пучок высокоэнергетичных
монохроматичных электронов рассеивается на встречном пучке мощного
лазера.

47.

• Преимущества монохроматизации фотонов в этом случае не слишком
перевешивают недостатки низкой интенсивности получаемого пучка и невысокой
точности проводимых с его помощью измерений, а также сложности технических
решений. Вследствие этого данный метод не получил широкого распространения
для исследований в области ГДР и используется в основном для получения
моноэнергетичных фотонов с энергией более 100 МэВ.
• Процесс поглощения ядром γ-кванта с энергией до ~ 50 МэВ приводит к тому, что
при снятии возбуждения ядро испускает отдельные нуклоны и их комбинации. Ядро
с наибольшей вероятностью испускает 1 нуклон, с меньшей вероятностью - 2 и
большее число нуклонов. Это обстоятельство вместе с соотношением энергетических
порогов соответствующих реакций определяет основные каналы распада ГДР.
Реакция, соответствующая каналу распада ГДР с образованием нуклона или их
комбинаций (γ,n), (γ,p), (γ,np), (γ,2n), (γ,3n) и т.п.), называется парциальной. Сумма
всех парциальных реакций описывает все возможные (за исключением рассеяния)
каналы выбывания фотонов из первичного пучка – реакцию полного
фотопоглощения
• (γ,абс) = (γ,n) + (γ,p) + (γ,np) + (γ,2n) + (γ,3n)+…. + (γ,n) + (γ,p) + (γ,2p) + (γ,3р) + …(γ,f)

48.

В области энергий максимума ГДР сечение фотопоглощения для
большинства тяжелых ядер в основном исчерпывается сечением (γ,n)
реакций (в области легких и средних ядер – суммой сечений (γ,n) и (γ,p)
реакций). За максимумом ГДР заметный вклад в сечение фотопоглощения
дают реакции с большей множественностью испускаемых нуклонов,
прежде всего реакции (γ,2n) и (γ,3n). Соотношение сечений реакций с
испусканием одного и двух нейтронов является важной характеристикой
процесса фоторасщепления, зависящей от механизма возбуждения и
распада ядра.
Так, например, расхождение энергетической зависимости сечения
реакции с испусканием одного нейтрона с предсказаниями
статистической модели, может служить доказательством проявления
процессов прямого выбивания нейтронов γ-квантами из ядра [14].
Однако обоснованность таких заключений в значительной степени
зависит от того, с какой точностью и надежностью определяется сечение
реакции (γ,n), то есть реакции с испусканием одного нейтрона, в той
области энергий, где энергетически возможен и процесс испускания двух
нейтронов в реакции (γ,2n).

49.

• В силу различных обстоятельств, основные из которых будут
рассмотрены ниже, во многих случаях данные по реакциям (γ,n) и
(γ,2n) оказываются взаимно связанными и влияющими друг на
друга. Такие данные, полученные в разных экспериментах,
существенно расходятся друг с другом [15 - 17]. Большинство данных
по реакциям (γ,n) и (γ,2n) получено в экспериментах с
квазимоноэнергетическими аннигиляционными фотонами в
Лоуренсовской Ливерморской национальной лаборатории (National
Lawrence Livermore Laboratory) США и Центре ядерных исследований
Франции (France Centre d’Etudes Nucleaires de Saclay) в Саклэ.
Причиной их существенных расхождений между собой являются
определенные недостатки использованных в экспериментах
процедур определения множественности фотонейтронов.

50. ЭЛЕКТРОЯДЕРНЫЕ РЕАКЦИИ

• - ядерные превращения, идущие при рассеянии электронов
атомными ядрами.
• Согласно
представлениям
квантовой
электродинамики,
рассеяние электронов на нуклоне происходит путём обмена
виртуальными γ-квантами. В большинстве случаев достаточно
ограничиться обменом одним γ-квантом.
• Отличие виртуальных γ-квантов от реальных состоит в том, что
для последних имеет место однозначная связь между
переданной нуклону энергией w и импульсом р.
• Для виртуальных γ-квантов такое равенство не имеет места, что
позволяет при рассеянии электронов варьировать независимо
каждую
кинематичическую
переменную.

51. ЭЛЕКТРОЯДЕРНЫЕ РЕАКЦИИ

• Если фиксировать только рассеянный электрон, то сечение
процесса выражается через две т. н. с т р у к т у р н ы е функции
ядра, которые зависят от переданной энергии и переданного
импульса.
• Одна (продольная) связана с распределением заряда в ядре, а
другая (поперечная)-с распределением тока намагниченности.
• На слайде показана зависимость первой структурной ф-ции R от
переданного ядру импульса p и энергии (2p/h)w (горизонтальная
ось).
• Если ядру не передаётся внутренняя энергия, то имеет место
процесс упругого рассеяния электронов.
• Соответствующая структурная функция (кривая 1), называется.
упругим формфактором, отражает распределение заряда ядра.

52. Зависимость первой структурной функции R от переданного ядру импульса p и энергии

Зависимость первой структурной функции R от
переданного ядру импульса p и энергии

53. ЭЛЕКТРОЯДЕРНЫЕ РЕАКЦИИ

• При очень больших переданных импульсах электрон "чувствует" кварковую структуру
ядерной системы. В асимптотической области функция R должна вести себя как
Q-2(n-1),
• где Q - переданный 4-импульс, n - число кварков в ядре (правило кваркового счёта).
• В случае нуклона (n = 3) асимптотическая область экспериментально достигнута и
соответствующая зависимость наблюдается.
• Для дейтрона область, где он ведёт себя как шестикварковая система (n = 6), и тем
более для ядер с большим числом нуклонов эта область ещё не достигнута.
Вторая структурная функция (упругий магнитный формфактор) характеризует
распределение тока намагниченности в ядре.
• В магнитный формфактор при больших переданных импульсах значительный вклад
приходится на двухчастичный обменный ток, а затем и кварковые степени свободы.

54.

• Кривая 2 отвечает случаю, когда р=w/c. Это условие реализуется при
поглощении реального g-кванта (см. Фотоядерные реакции).
• Кривая 3 даёт срез структурной ф-ции при фиксированном значении
переданного импульса. При малых значениях переданной энергии в
структурной ф-ции проявляются узкие пики, отвечающие возбуждению
дискретных и квазидискретных состояний ядра. Далее следует
широкий пик, отвечающий возбуждению мультипольных гигантских
ре-зонансов (ГР)- монопольных, дипольных, квадрупольных и более
высокой мультипольности. Механизм распада гигантских резонансов,
возбуждаемых при рассеянии электронов, аналогичен механизму
распада при поглощении g-квантов.

55.

• Следующий пик в структурной ф-ции проявляется при
энергии wp2/2M+<B>, где M - масса нуклона, <B> - ср. энергия связи
нуклона в ядре. Это пик квазиупругого выбивания нуклона из ядра
(КУ). Измерения на совпадение рассеянного электрона и выбитого
нуклона (или нук-лонной ассоциации) позволяют получить данные об
их распределении по импульсам (см. Совпадений метод).
• При большей энергии наблюдается ещё один пик в структурной ф-ции.
Он связан с рассеянием электрона на одном нуклоне, в результате чего
возбуждаются нуклон-ные степени свободы, и в первую очередь Dизобара (1232). Аналогичная картина имеет место и при поглощении gкванта (см. Резонансы).

56.

57.

58. Литература

• Айзенберг И. М., Грайнер В., Механизмы возбуждения ядра, пер.
с англ., М., 1973; Широков Ю. М., Юдин Н. П., Ядерная физика, М.,
1972; Левинджер Д ж., Фотоядерные реакции, пер. с англ., М.,
1962.
• Берестецкий В. Б., Лифшиц E. M., Питаев-ский Л. П., Квантовая
электродинамика, 3 изд., M., 1989; Drechsel D., Giannini M. M.,
Electron-scattering off nuclei, "Repts. Progr. Phys.", 1989, v. 52, p.
1083; Ахиезер А. И., Ситен-KO А. Г., Тартаковский В. К.,
Электродинамика ядер, К., 1989.