Взаимодействие частиц и излучений с веществом

1. Взаимодействие частиц и излучений с веществом

Государственный университет «Дубна»
Инженерно-физический институт
Кафедра ядерной физики
Кафедра фундаментальных проблем физики микромира
Специальный семинар по физике ядра и ядерным реакциям
Взаимодействие частиц и
излучений с веществом
Выполнила студентка группы 4162
Бетенева В.В.
2019

2. Основные процессы взаимодействия заряженных частиц со средой

1.
2.
3.
4.
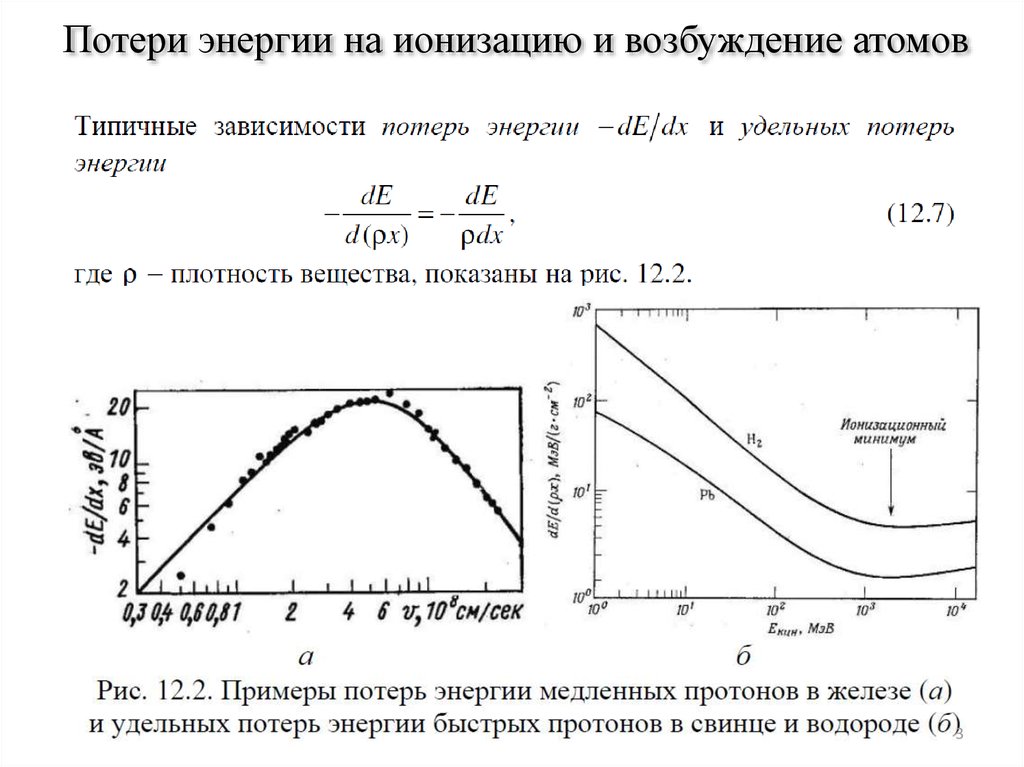
Потери энергии на ионизацию и возбуждение атомов
Тяжелые заряженные частицы теряют свою энергию в основном в результате
кулоновского взаимодействия при столкновениях со связанными атомными
электронами. При этом электроны могут перескакивать на более высокие дискретные
уровни (возбуждение), а могут и отрываться от атома (ионизация). Если пролетающая
через вещество частица обладает энергией, большей энергии связи электрона в атоме,
то преобладают процессы ионизации.
Потери энергии и многократное рассеяние при упругом рассеянии
При пролете заряженной частицы через атом в непосредственной близости от ядра
происходит кулоновское взаимодействие с ядром, так как прицельный параметр
настолько мал, что кулоновское поле ядра не экранируется полем атомных электронов.
Потери энергии на упругое взаимодействие с ядрами составляют около 0.03% от
ионизационных потерь, т.е. дают незначительный вклад в общие потери энергии.
При прохождении через вещество частицы претерпевают многократное рассеяние.
Тормозное излучение
Это электромагнитное излучение заряженной частицы, возникающее в результате ее
торможения при взаимодействии с электростатическим полем атомного ядра и
атомных электронов.
Излучение Вавилова-Черенкова
При движении заряженной частицы в среде со скоростью, превышающей фазовую
скорость света в этой среде, возникает специфическое свечение, названное излучением
Вавилова-Черенкова.
2

3. Потери энергии на ионизацию и возбуждение атомов

3

4. Ионизационное торможение заряженных частиц

Ионизация и возбуждение атомов среды являются главным механизмом потерь
энергии при прохождении тяжелой заряженной частицы через вещество. В этом
механизме кинетическая энергия заряженной частицы тратится на возбуждение и
ионизацию атомов среды, через которую она проходит.
Ионизационные потери для тяжёлых заряженных частиц можно описать при
помощи следующей приближенной формулы:
Данная формула была впервые сформулирована Феликсом Блохом и Хансом Бете и
в последствии была названа в их честь.
Здесь z – заряд частицы, летящей со скоростью v в веществе с плотностью
электронов .
(эрг) ‒ средний потенциал возбуждения атомов поглощающего
вещества ( в эВ: I 13.5Z 10Z (эВ)).
Основной результат, вытекающий из этой формулы, заключается в том, что
удельные потери энергии заряженной частицы на ионизацию пропорциональна
квадрату заряда частицы, концентрации электронов в среде, некоторой функции от
скорости
и не зависит от массы налетающей частицы. Это получается из-за
того, что происходит взаимодействие электрических зарядов частиц, а не их масс.
4

5. Ионизационное торможение заряженных частиц

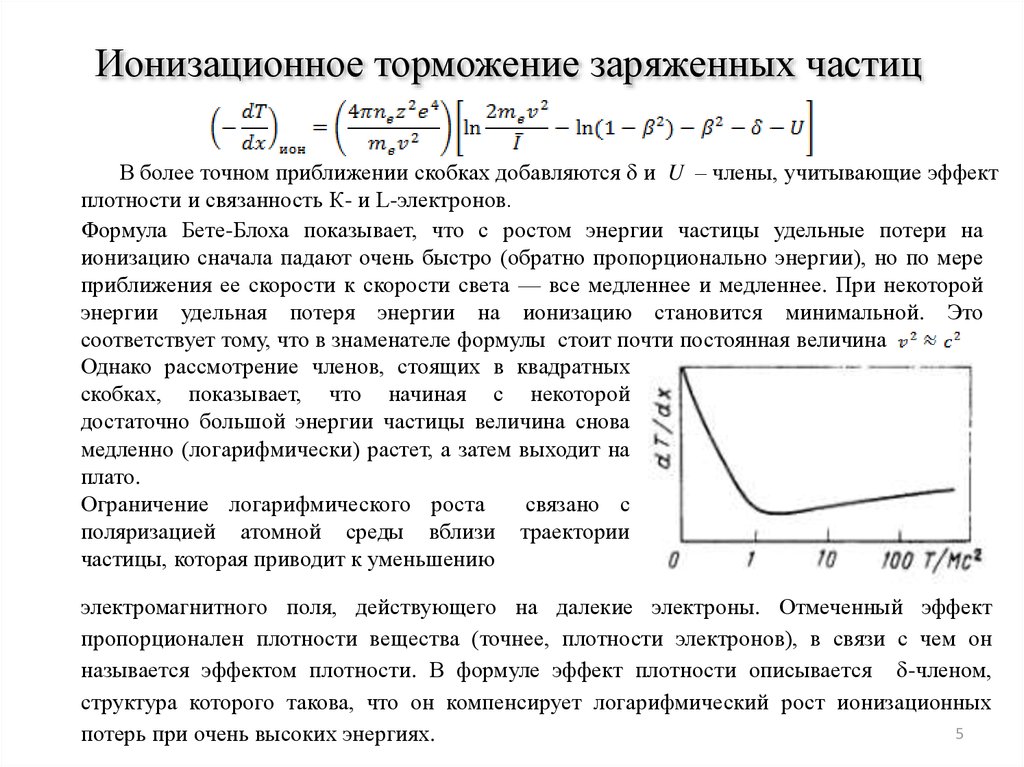
В более точном приближении скобках добавляются d и U ‒ члены, учитывающие эффект
плотности и связанность К- и L-электронов.
Формула Бете-Блоха показывает, что с ростом энергии частицы удельные потери на
ионизацию сначала падают очень быстро (обратно пропорционально энергии), но по мере
приближения ее скорости к скорости света — все медленнее и медленнее. При некоторой
энергии удельная потеря энергии на ионизацию становится минимальной. Это
соответствует тому, что в знаменателе формулы стоит почти постоянная величина
Однако рассмотрение членов, стоящих в квадратных
скобках, показывает, что начиная с некоторой
достаточно большой энергии частицы величина снова
медленно (логарифмически) растет, а затем выходит на
плато.
Ограничение логарифмического роста
связано с
поляризацией атомной среды вблизи траектории
частицы, которая приводит к уменьшению
электромагнитного поля, действующего на далекие электроны. Отмеченный эффект
пропорционален плотности вещества (точнее, плотности электронов), в связи с чем он
называется эффектом плотности. В формуле эффект плотности описывается d-членом,
структура которого такова, что он компенсирует логарифмический рост ионизационных
5
потерь при очень высоких энергиях.

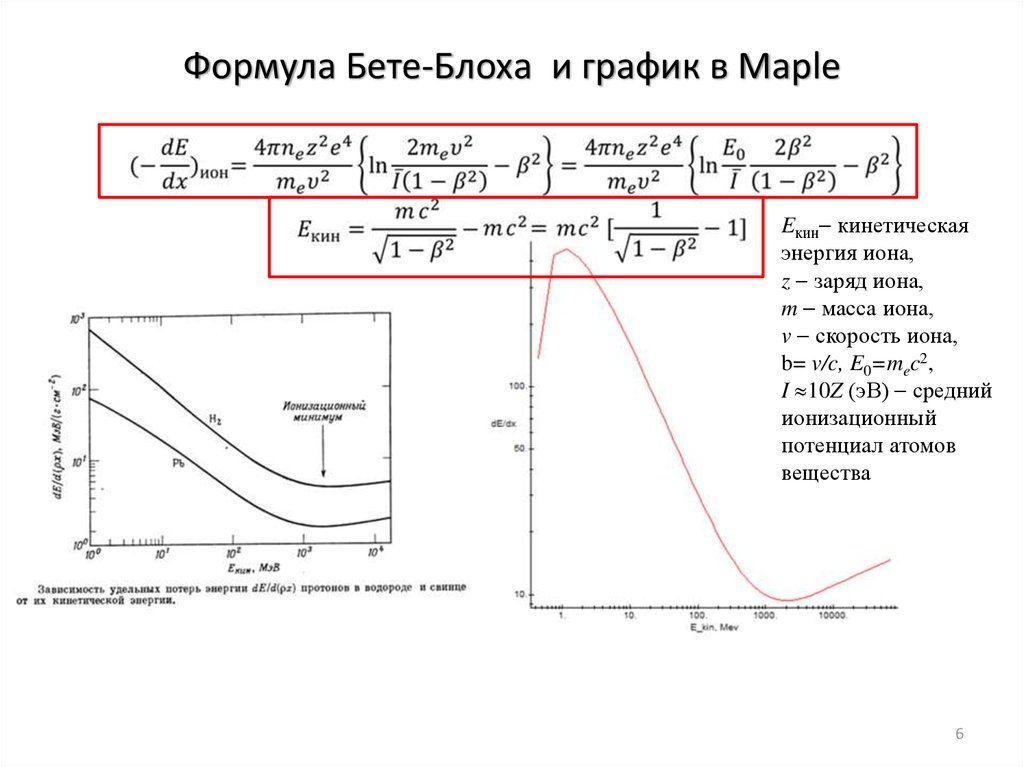
6. Формула Бете-Блоха и график в Maple

Eкин кинетическая
энергия иона,
z заряд иона,
m масса иона,
v скорость иона,
b= v/c, E0=mec2,
I 10Z (эВ) средний
ионизационный
потенциал атомов
вещества
6

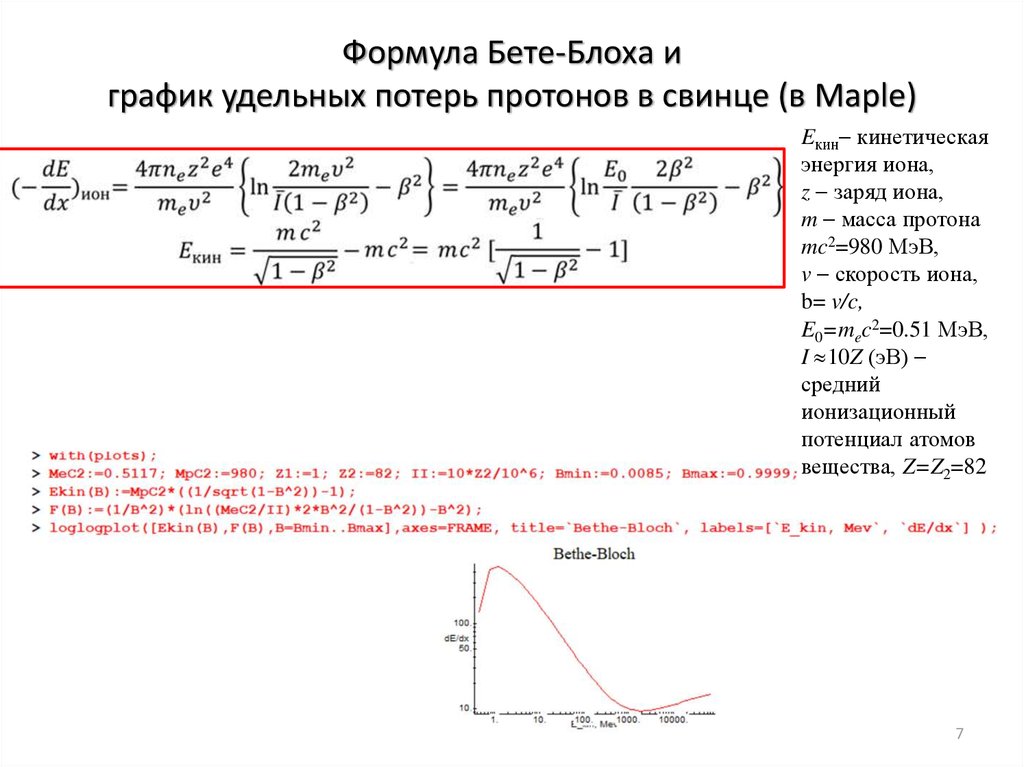
7. Формула Бете-Блоха и график удельных потерь протонов в свинце (в Maple)

Eкин кинетическая
энергия иона,
z заряд иона,
m масса протона
mc2=980 МэВ,
v скорость иона,
b= v/c,
E0=mec2=0.51 МэВ,
I 10Z (эВ)
средний
ионизационный
потенциал атомов
вещества, Z=Z2=82
7

8. Ионизационное торможение электронов

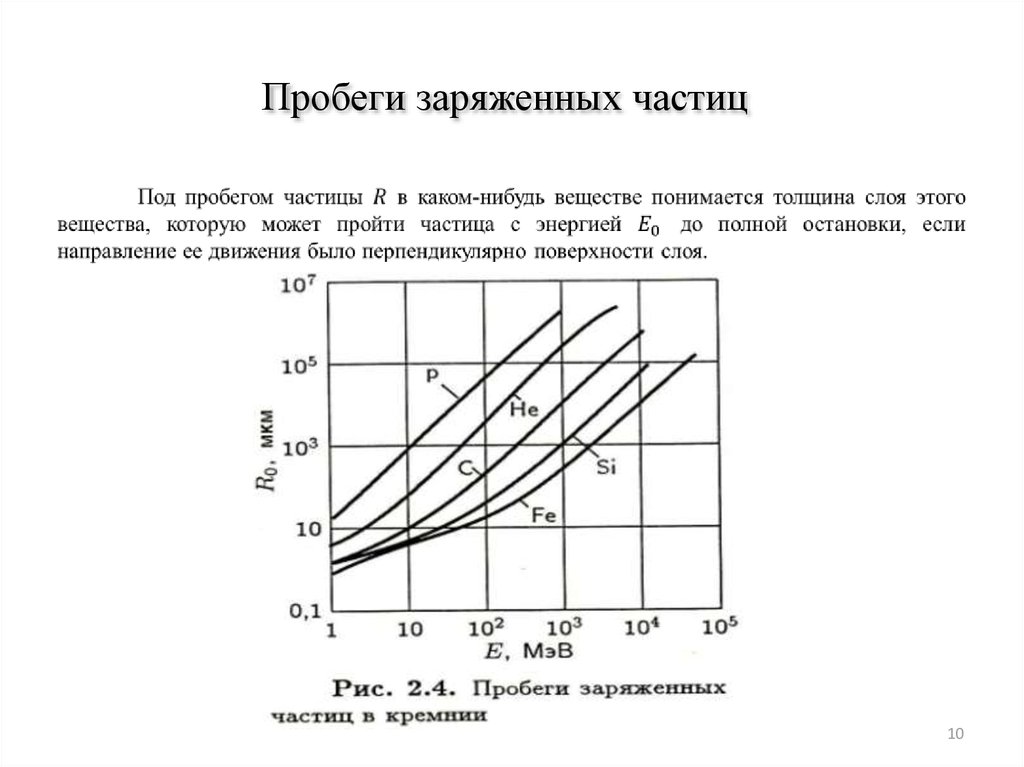
8

9. Пробеги заряженных частиц

9

10. Пробеги заряженных частиц

10

11. Пробеги заряженных частиц

Траектории заряженных частиц в веществе у легких и тяжелых частиц различны. У последних они почти
прямолинейны, а электроны многократно рассеиваются на значительные углы. На кривых изображена
зависимость числа моноэнергетических частиц, прошедших поглотитель.
Для монохроматического пучка α-частиц теоретическая кривая (1, сплошная) удовлетворительно совпадает с
экспериментом (2, пунктир). Конечный участок экспериментальной кривой не вертикален, а имеет небольшой
наклон вследствие статистического характера процесса потери энергии. Частицы теряют свою энергию в очень
большом, но конечном числе отдельных актов. Флуктуации подвержено как число таких актов на единицу длины,
так и потери энергии в каждом отдельном акте. В соответствии с этим и пробеги α-частиц испытывают
статистические флуктуации. Однако величина разброса пробега незначительна и составляет приблизительно 1%
от полного пробега для α-частиц с энергией 5 МэВ. Поэтому по пробегу α-частицы можно с хорошей степенью
точно определять их энергию.
Электроны же испытывают в веществе многократное рассеяние, направление их движения часто меняется и
только в наиболее благоприятных случаях электроны проходят максимальное расстояние в поглотителе в
направлении, перпендикулярном к его поверхности. Кривая поглощения коллимированного пучка
моноэнергетических электронов имеет вид, отличный от аналогичной кривой для α-частиц. Поэтому энергию
электронов нельзя определять по пробегу, а надо измерять полную ионизацию, произведенную им в веществе.
11

12. Пробеги электронов

12

13. Радиационное торможение.

При быстром торможении заряженной частицы в электрическом поле атомного ядра
и атомных электронов испускается тормозное излучение. Потери энергии на тормозное
излучение (радиационные потери)
пропорциональны квадрату ускорения.
Поскольку силы F кулоновского взаимодействия с ядрами для частиц с равными
зарядами z одинаковы, то
Радиационные потери энергии для частиц с
равными зарядами обратно пропорциональны
квадрату
массы
частицы.
Особенно
существенны для легчайших заряженных
частиц.
Известным
примером
тормозного
излучения электронов является непрерывный
рентгеновский спектр, возникающий при
торможении электронов на аноде рентгеновской
трубки.
13
Длина волны рентгеновского излучения

14. Взаимодействие нейтронов с веществом

Электромагнитное взаимодействие нейтрона с электроном определяется
взаимодействием магнитных моментом. Но оно настолько мало, что сечение
ионизационного торможения нейтрона оказывается в
раз меньше, чем для
заряженной частицы.
Эффект от взаимодействия магнитных моментов нейтрона и электрона становится
заметным только тогда, когда магнитные момент всех электронов ориентированы
одинаковым образом (в ферромагнетиках). В этом случае взаимодействие магнитных
моментов нейтрона и электронов приводит к макроскопическому эффекту
дополнительного рассеяния, излучение которого позволяет оценить магнитный момент
нейтрона.
Основным видом взаимодействия нейтронов с веществом является их
взаимодействие с атомными ядрами. В зависимости от того, попадёт нейтрон в ядро
или нет, его взаимодействие с ядрами можно разделить на два класса:
1. Упругое потенциальное рассеяние на ядерных силах без попадания нейтрона в ядро
(n,n);
2. Ядерные реакции типов (n, γ), (n,p), (n,α), реакция деления и др.; неупругое
рассеяние (n,n’), упругое рассеяние с заходом нейтрона в ядро – упругое резонансное
рассеяние (n,n);
14

15. Взаимодействие нейтронов с веществом

Относительная роль каждого процесса определяется соответствующим сечением. В
некоторых веществах, для которых роль упругого рассеяния относительно высока,
быстрый нейтрон теряет свою энергию в серии последовательных актов упругого
соударения с ядрами вещества (замедление нейтронов). Процесс замедления
продолжается до тех пор, пока кинетическая энергия нейтрона не сравняется с энергией
теплового движения атомов замедляющего вещества (замедлителя). Такие нейтроны
называют тепловыми. К числу лучших замедлителей, широко используемых в ядерной
физике и ядерной технике для превращения быстрых нейтронов в тепловые,
относятся вода, тяжёлая вода, бериллий, графит. Поскольку в этих замедлителях,
содержащих лёгкие ядра, потери на поглощение малы. Дальнейшие столкновения
тепловых нейтронов с атомами замедлителя практически не изменяют энергии
нейтронов и приводят только к перемещению их в пространстве (диффузия тепловых
нейтронов), которое продолжается до тех пор, пока нейтрон не поглотится ядром.
Вопросы взаимодействия быстрых и медленных нейтронов со средой чрезвычайно
важны при рассмотрении различных задач нейтронной физики и, в частности, для
конструирования ядерных реакторов.
15

16. Взаимодействие γ-излучения с веществом

Изменение интенсивности тонкого пучка гамма- (или рентгеновского) излучения
происходит по экспоненциальному закону (закону Бугера)
где Io – начальная интенсивность, x – пройденное в веществе расстояние. Величину
называют линейным коэффициентом поглощения гамма-излучения. Величину μγ
называют линейным коэффициентом поглощения гамма-излучения .
Зависимость полного коэффициента
поглощения гамма-лучей в алюминии.
16

17. Взаимодействие γ-излучения с веществом

Основными видами взаимодействия γ-излучения с веществом являются:
• Атомный фотоэффект
• Эффект Комптона
• Образование электрон-позитронных пар
17

18. Атомный фотоэффект

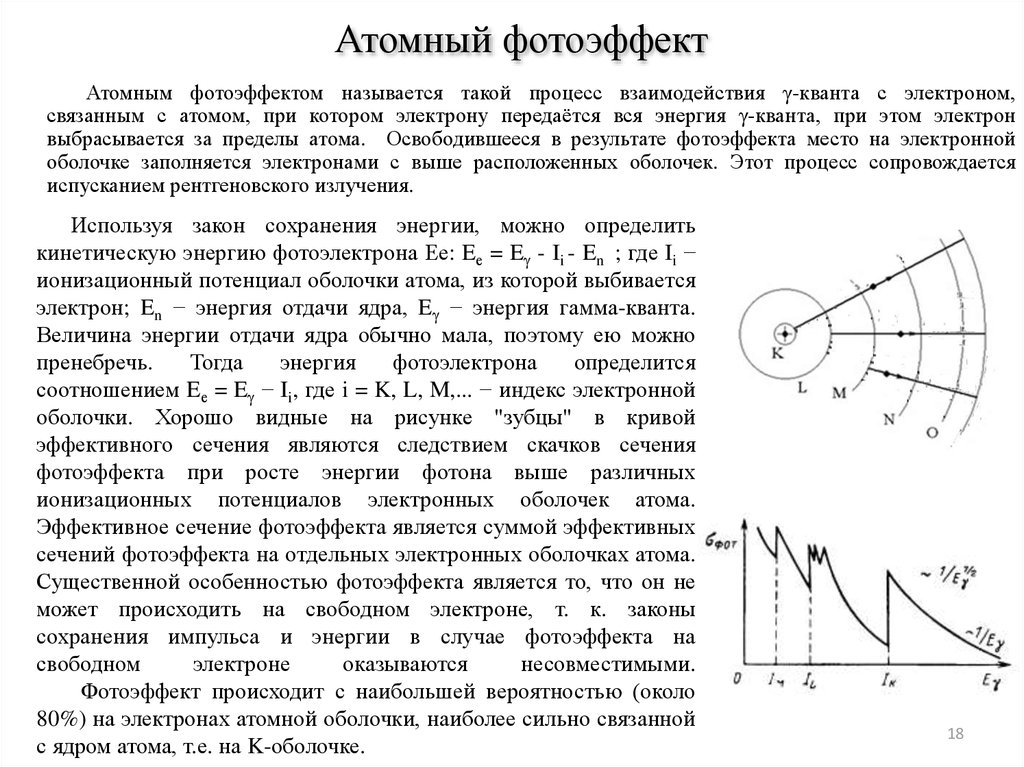
Атомным фотоэффектом называется такой процесс взаимодействия γ-кванта с электроном,
связанным с атомом, при котором электрону передаётся вся энергия γ-кванта, при этом электрон
выбрасывается за пределы атома. Освободившееся в результате фотоэффекта место на электронной
оболочке заполняется электронами с выше расположенных оболочек. Этот процесс сопровождается
испусканием рентгеновского излучения.
Используя закон сохранения энергии, можно определить
кинетическую энергию фотоэлектрона Eе: Eе = Eγ - Ii - En ; где Ii −
ионизационный потенциал оболочки атома, из которой выбивается
электрон; En − энергия отдачи ядра, Eγ − энергия гамма-кванта.
Величина энергии отдачи ядра обычно мала, поэтому ею можно
пренебречь.
Тогда
энергия
фотоэлектрона
определится
соотношением Eе = Eγ − Ii, где i = K, L, M,... − индекс электронной
оболочки. Хорошо видные на рисунке "зубцы" в кривой
эффективного сечения являются следствием скачков сечения
фотоэффекта при росте энергии фотона выше различных
ионизационных потенциалов электронных оболочек атома.
Эффективное сечение фотоэффекта является суммой эффективных
сечений фотоэффекта на отдельных электронных оболочках атома.
Существенной особенностью фотоэффекта является то, что он не
может происходить на свободном электроне, т. к. законы
сохранения импульса и энергии в случае фотоэффекта на
свободном
электроне
оказываются
несовместимыми.
Фотоэффект происходит с наибольшей вероятностью (около
80%) на электронах атомной оболочки, наиболее сильно связанной
с ядром атома, т.е. на K-оболочке.
18

19. Эффект Комптона

Детальное изучение рассеяния электромагнитного излучения с изменением длины
волны было проведено в 1923г. Комптоном.
Он предложил квантовую интерпретацию явления рассеяния,
согласно которой рентгеновское излучение надо рассматривать
как поток частиц-фотонов, упруго рассеивающихся на других
частицах – электронах.
При рассеянии фотона на свободном электроне частоты фотона ν и ν ’(до и после
рассеяния соответственно) связаны соотношением:
Θ – угол рассеяния. Перейдя к длинам волн:
- Комптоновская длина волны электрона.
Эффект
Комптона
является
одним
из
доказательств
справедливости корпускулярно-волнового дуализма микрочастиц и подтверждает
существование фотонов.
Формула для вычисления дифференциального сечения комптоновского рассеяния
была получена Клейном, Нишиной и Таммом, и имеет вид:
19

20. Образование электрон-позитронных пар

При достаточно высокой энергии γ-кванта наряду с фотоэффектом и эффектом Комптона
может происходить третий вид взаимодействия – образование электрон-позитронных пар.
Возможность такого процесса была обнаружена в 1928г. Дираком в результате анализа
релятивистского квантовомеханического уравнения для электрона.
Данный процесс не может происходить в вакууме, а требует обязательного соседства ядра
или электронов. Непосредственно это следует из законов сохранения энергии и импульса. В
присутствии ядра или электрона процесс образования пары возможен, так как можно
распределить энергию и импульс γ-кванта между тремя частицами без противоречия с
законами сохранения. При это если процесс образования пары идёт в кулоновском поле ядра
или протона, то энергия образующегося ядра отдачи оказывается весьма малой, так что
пороговая энергия γ-кванта Ео, необходимая для образования пары, практически совпадает с
удвоенной массой покоя электрона:
Выражение для сечения образования электрон-позитронных
пар имеет достаточно сложный вид. Его можно представить
в аналитическом виде только для ограниченного интервала
значений энергии.
20

21. Общий характер взаимодействия γ-излучения с веществом

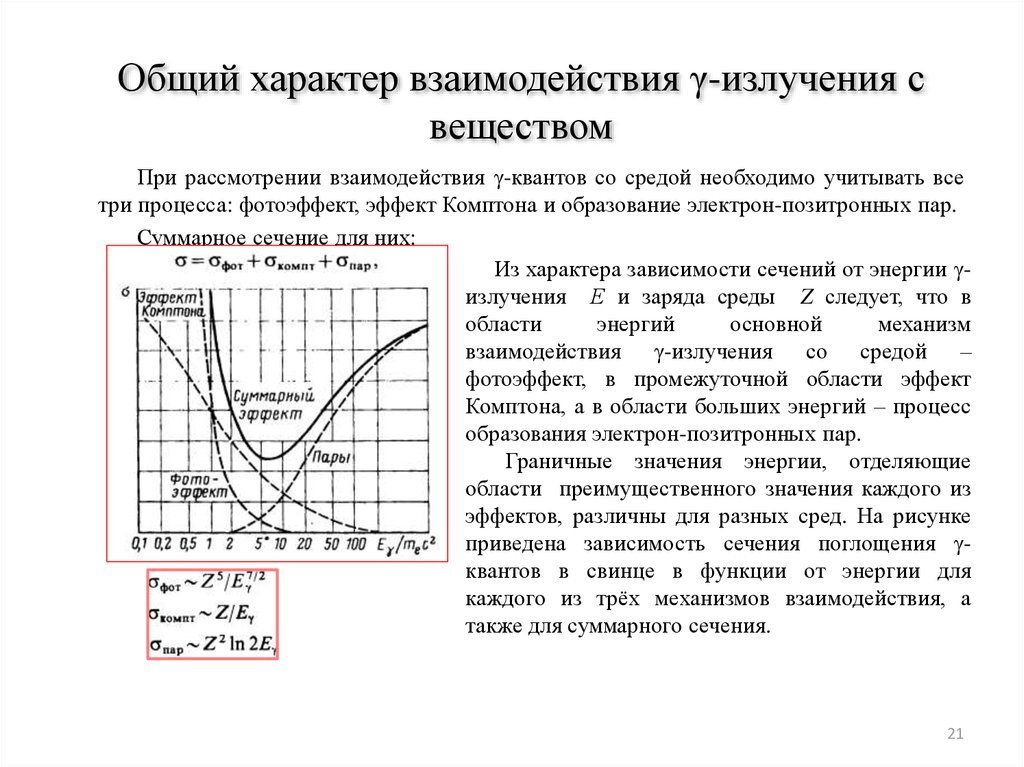
При рассмотрении взаимодействия γ-квантов со средой необходимо учитывать все
три процесса: фотоэффект, эффект Комптона и образование электрон-позитронных пар.
Суммарное сечение для них:
Из характера зависимости сечений от энергии γизлучения Е и заряда среды Z следует, что в
области
энергий
основной
механизм
взаимодействия γ-излучения со средой –
фотоэффект, в промежуточной области эффект
Комптона, а в области больших энергий – процесс
образования электрон-позитронных пар.
Граничные значения энергии, отделяющие
области преимущественного значения каждого из
эффектов, различны для разных сред. На рисунке
приведена зависимость сечения поглощения γквантов в свинце в функции от энергии для
каждого из трёх механизмов взаимодействия, а
также для суммарного сечения.
21

22. Литература

1.
2.
3.
4.
5.
6.
7.
8.
К.Н. Мухин. "Экспериментальная ядерная физика" (в трех томах),
СПб., Издательство Лань,. 2008;
Ю.М. Широков и Н.П. Юдин. Ядерная физика. М.: Наука, 1972
Основная;
Фрауэнфельдер Г. Субатомная физика. - М.: Мир, 1979;
Введение в физику тяжелых ионов: Учебное пособие / Под. ред.
Ю.Ц. Оганесяна. М.: МИФИ, 2008;
Ракобольская И.В. Ядерная физика. - М.: Изд-во Моск.ун-та, 1981;
nuclphys.sinp.msu.ru/chpartint/index.html А.М. Анохина, В.И. Галкин,
Е.А. Мурзина. Материалы спецкурса: Взаимодействие заряженных
частиц с веществом;
mtk.jinr.ru
Ю.В. Готт Взаимодействие частиц с веществом в плазменных
исследованиях. М. Атомиздат. 1978.
22