Взаимодействие заряженных частиц со средой

1. Взаимодействие заряженных частиц со средой

Государственный университет «Дубна»
Факультет естественных и инженерных наук
Кафедра Ядерной физики
Специальный семинар по физике ядра и ядерным реакциям
Юненко К.Е.
Взаимодействие заряженных частиц со средой
2017
1

2. Вопрос 11. Взаимодействие заряженных частиц со средой.

• Потери энергии на ионизацию и возбуждение
атомов.
• Пробеги заряженных частиц.
2

3. Потери энергии на ионизацию и возбуждение атомов

При прохождении через вещество частица тратит
кинетическую энергию на возбуждение и ионизацию
атомов той среды, через которую она проходит.
Пусть ze – заряд частицы, – её скорость, ρ –
расстояние от свободного электрона,
, где М
– масса частицы,
- масса электрона, -e – его заряд.
Можно считать, что взаимодействие происходит на
участке, равным 2ρ.
p
F
Взаимодействие частицы с электроном
dt
t 2
p 2 ze 2
Взаимодействие частицы с цилиндрическим
слоем электронов
Соответствующая кинетическая энергия, которую
теряет частица:
T p 2 2me (2 z 2 e 4 meV 2 )(1 2 )
Для учёта взаимодействия со всеми имеющимися
электронами выстраивается цилиндрический слой,
где ρ – его радиус, dρ - толщина, dx – высота, ne плотность электронов. Число электронов в этом слое:
Vne 2 ne d dx .Тогда потери энергии на единицу
2 4
длины: dT ( ) TVne ( 4 ne z e )( d )
dx
dx
me 2

4. Потери энергии на ионизацию и возбуждение атомов

Полная удельная потеря энергии при интегрировании в пределах от м ин до м акс :
dT
dx
ма кс
ми н
4 ne z 2 e 4
dT
( )d
ln м акс
2
dx
me
м ин
Условие для м ин :
Tм акс (2 z 2e 4 (me 2 ))(1 м2 ин ) 2me 2
м ин ze 2 (me 2 )
м акс связано со значением среднего ионизационного потенциала.
Также при вычислении ln м акс следует учесть релятивистские эффекты, такие как: возрастание
м ин
максимальной передаваемой энергии, потери на излучение Вавилова-Черенкова и другие.

5. Потери энергии на ионизацию и возбуждение атомов

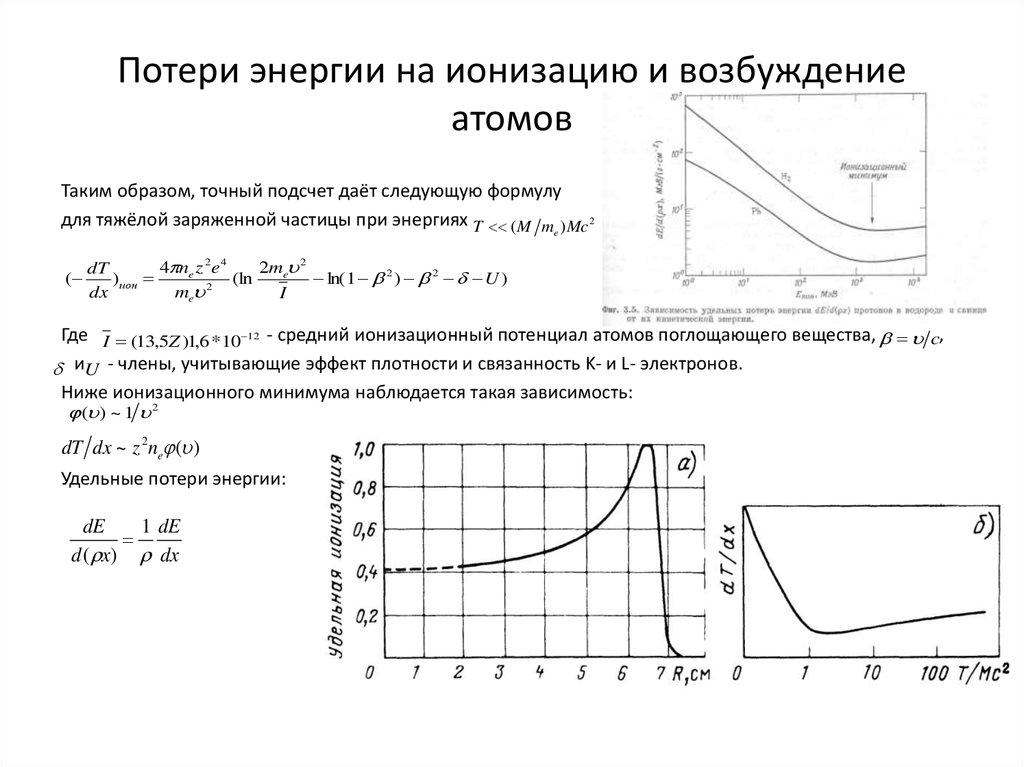
Таким образом, точный подсчет даёт следующую формулу
для тяжёлой заряженной частицы при энергиях T ( M m ) Mc 2 :
e
4 ne z 2e 4
2me 2
dT
(
)ион
(ln
ln( 1 2 ) 2 U )
2
dx
me
I
Где I (13,5Z )1,6 *10 12 - средний ионизационный потенциал атомов поглощающего вещества, c,
иU - члены, учитывающие эффект плотности и связанность K- и L- электронов.
Ниже ионизационного минимума наблюдается такая зависимость:
( ) ~ 1 2
dT dx ~ z 2 ne ( )
Удельные потери энергии:
dE
1 dE
d ( x) dx

6. Потери энергии на ионизацию и возбуждение атомов

Для электронов формула выглядит несколько иначе:
(
2 ne e 4
Te me 2
dT
)ион
(ln
ln 2(2 1 2 1 2 ) 1 2 1 8(1 1 2 ) 2 )
2
2
2
dx
me
2 I (1 )
Где Te - релятивистская кинетическая энергия электрона, ne - плотность электронов в среде, - поправка
на эффект плотности.
Причём , при энергиях электронов превышающих критическую энергию, большую роль начинает играть
тормозное излучение, а не эффект плотности.
Eкр
600 МэВ
Z

7. Пробеги заряженных частиц

Случай а соответствует прохождению тяжёлой заряженной частицы, в то время, как случай б
соответствует прохождению фотонов через вещество (электроны же являются промежуточным
случаем).

8. Большое число слабо отклоняющих взаимодействий

Множество взаимодействий во время
прохождения частицей вещества приводят к
потере энергии и отклонению траектории
частицы. Вследствие этого пучок, входящий в
вещество, перестаёт быть моноэнергетическим и
становится расходящимся.
Вплоть до некоторой определённой толщины
поглощающего слоя вещества через него
проходят почти все частицы пучка свободно. При
увеличении толщины отдельные частицы
начинают застревать. При достижении толщины
R0 (средняя длина пробега) половина частиц
поглощается. В конечном итоге поглощаются все
частицы в пучке.
N(x) – число частиц пучка, прошедших через слой х,
Rэкстр - экстраполированная длина пробега

9. Взаимодействие типа «всё или ничего»

Данный тип взаимодействия характеризуется тем,
что проходящая частица либо поглощается
веществом, либо свободно проходит через него,
не меняя энергию и направления. Для каждого
элементарного слоя число частиц, испытавших
взаимодействие, пропорционально числу
падающих частиц. Получаем:
dN N ( x) dx
N ( x) N (0)e x
где - коэффициент поглощения.
Можно определить также величину 1 ,
называемую средней длиной свободного
пробега.

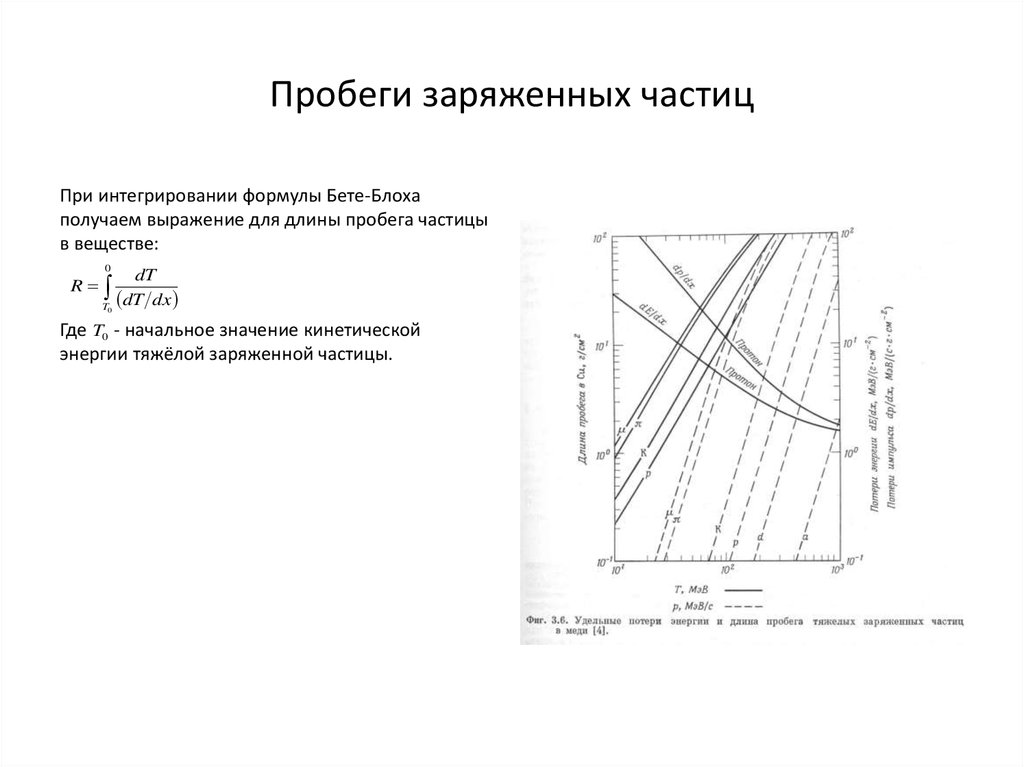
10. Пробеги заряженных частиц

При интегрировании формулы Бете-Блоха
получаем выражение для длины пробега частицы
в веществе:
0
R
dT
dx
dT
T0
Где T0 - начальное значение кинетической
энергии тяжёлой заряженной частицы.

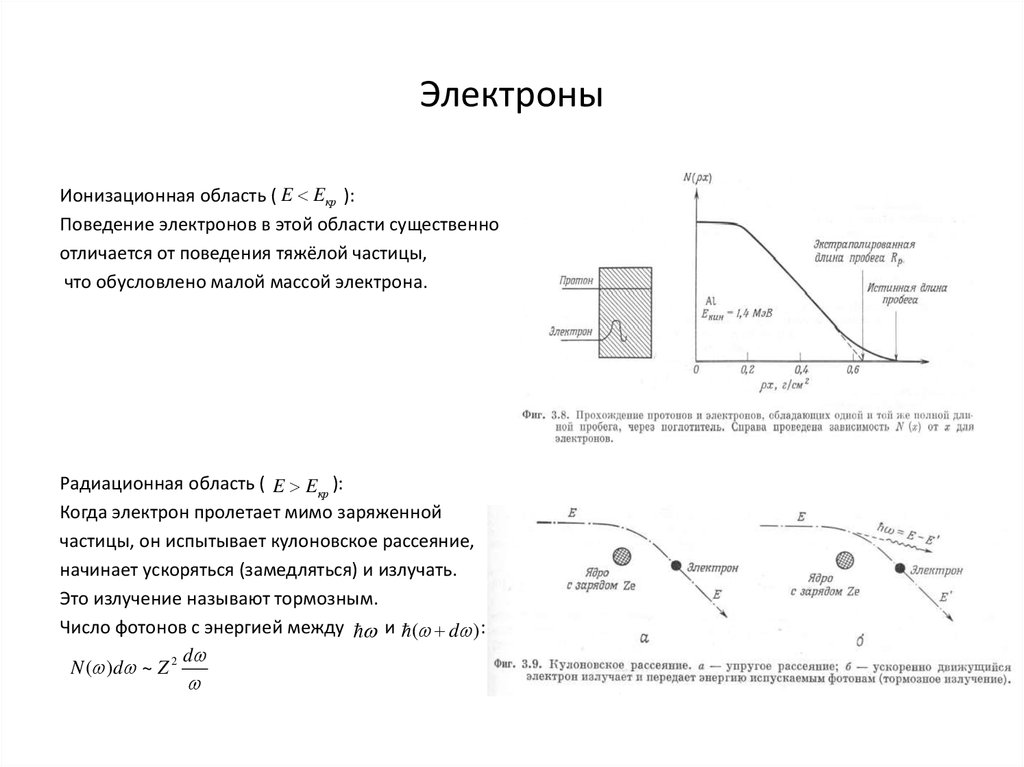
11. Электроны

Ионизационная область ( E Eкр ):
Поведение электронов в этой области существенно
отличается от поведения тяжёлой частицы,
что обусловлено малой массой электрона.
Радиационная область ( E Eкр ):
Когда электрон пролетает мимо заряженной
частицы, он испытывает кулоновское рассеяние,
начинает ускоряться (замедляться) и излучать.
Это излучение называют тормозным.
Число фотонов с энергией между и ( d ) :
d
N ( )d ~ Z 2

12. Электроны. Радиационная область

Расстояние, на котором энергия электрона
уменьшится в e раз, называется радиационной
длиной и обозначается X 0 . Потери энергии на
излучение при больших энергиях электронов:
E
dE
dx рад X 0
или
E E0 e x X 0
Испущенные фотоны обладают энергией большей
1МэВ, поэтому происходит рождение электроннопозитронных пар. Из-за этого создаются
каскадные ливни.
В итоге фактическая длина среднего свободного
пробега будет:
9
X р X0
7

13. Задание

Построить в MathCAD график зависимости ионизационных
потерь тяжёлых частиц от их скорости (формула Бете-Блоха).

14. Литература

1.
2.
К.Н. Мухин. "Экспериментальная ядерная физика" (в трех томах), СПб., Издательство Лань,. 2009.
Фрауэнфельдер Г. Субатомная физика. - М.: Мир, 1979