Алгоритмы и структуры данных. Алгоритмические основы обработки данных

1.

Алгоритмы и структуры
данных.
Алгоритмические основы
обработки данных.
Лектор –Лупин Сергей Сергеевич, к.т.н., доцент
16 лекций
8 семинаров
4 лабораторных*
Итог – дифф. зачет

2.

Алгоритмы и
структуры
данных
• Модуль 1. Методы сортировки.
• Лекция 1. Сортировка в линейных структурах.

3.

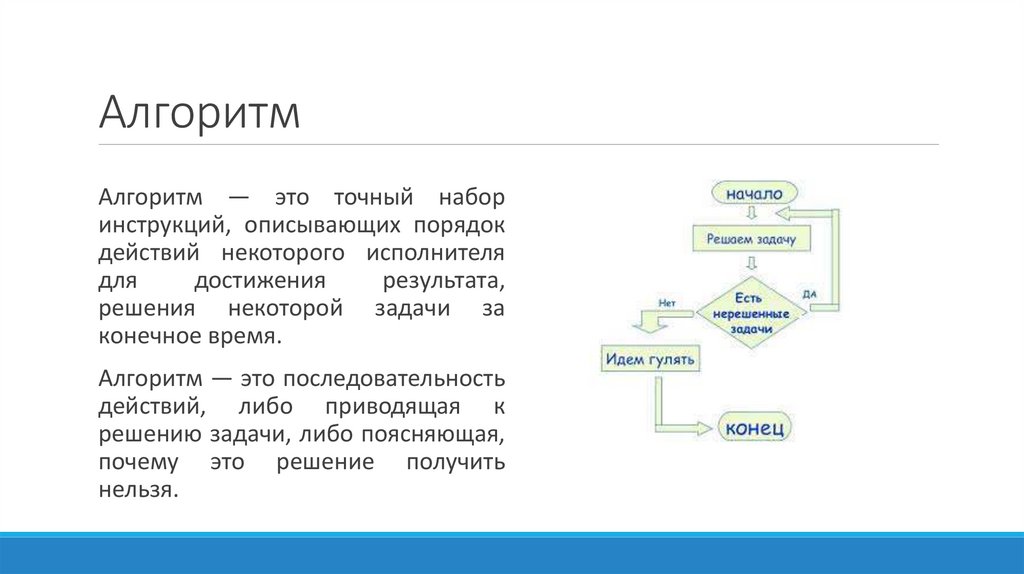
Алгоритм
Алгоритм — это точный набор
инструкций, описывающих порядок
действий некоторого исполнителя
для
достижения
результата,
решения некоторой задачи за
конечное время.
Алгоритм — это последовательность
действий, либо приводящая к
решению задачи, либо поясняющая,
почему это решение получить
нельзя.

4.

Информация
Знания о предметах, фактах, идеях
и т. д., которыми могут обмениваться
люди в рамках конкретного контекста
(ISO/IEC 10746-2:1996);
Знания
относительно
фактов,
событий, вещей, идей и понятий,
которые в определённом контексте
имеют конкретный смысл (ISO/IEC
2382:2015).

5.

Данные
Данные — поддающееся многократной
интерпретации
представление
информации в формализованном виде,
пригодном для передачи, связи или
обработки (ISO/IEC 2382:2015).
Данные — формы представления
информации, с которыми имеют дело
информационные
системы
и их
пользователи (ISO/IEC 10746-2:1996).

6.

Структура данных
• Программная
единица,
позволяющая
хранить
и
обрабатывать множество однотипных
и/или логически связанных данных в
вычислительной технике.
«Плохие программисты думают о
коде.
Хорошие
программисты
думают о структурах данных и их
взаимосвязях»,
— Линус Торвальдс, создатель Linux.

7.

Программа
«Программы =
алгоритмы + структуры
данных» - Никлаус Вирт.

8.

Типы структур данных
Линейные
структуры
—
структуры, в которых связи между
элементами
не
зависят
от
выполнения какого-либо условия.
Нелинейные
структуры
—
структуры, у которых связи между
элементами
зависят
от
выполнения
определенного
условия.

9.

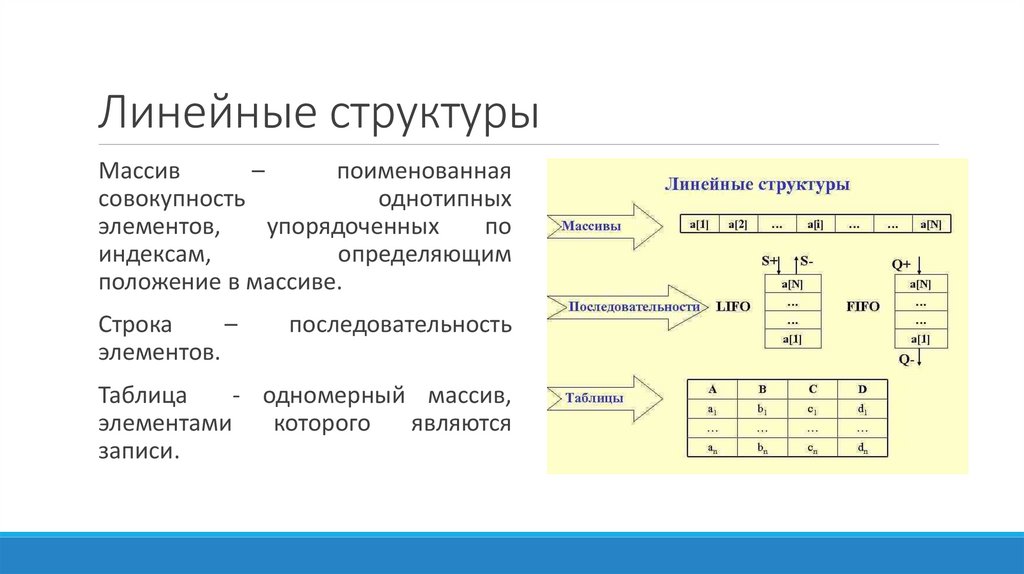
Линейные структуры
Массив
–
поименованная
совокупность
однотипных
элементов,
упорядоченных
по
индексам,
определяющим
положение в массиве.
Строка
–
элементов.
последовательность
Таблица
- одномерный массив,
элементами
которого
являются
записи.

10.

Сортировка
Упорядочение элементов множества в возрастающем
или убывающем порядке.
С упорядоченными элементами проще работать, чем с
произвольно
расположенными:
легче
найти
необходимые элементы, исключить, вставить новые.
Сортировка применяется при трансляции программ,
при организации наборов данных на внешних
носителях, при создании библиотек, каталогов, баз
данных и т.д.
Обычно сортируемые элементы множества называют
записями и обозначают через k1, k2, …,kn .

11.

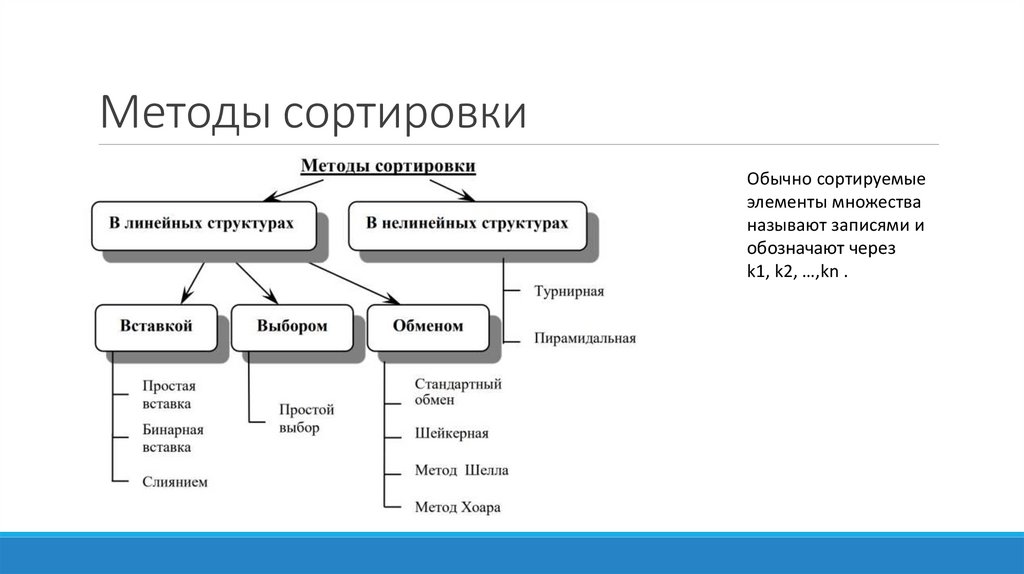
Методы сортировки
Обычно сортируемые
элементы множества
называют записями и
обозначают через
k1, k2, …,kn .

12.

Сортировка выбором
Сортировка выбором состоит в том, что сначала
в неупорядоченном списке выбирается и
отделяется от остальных наименьший элемент.
После этого исходный список оказывается
изменённым. Изменённый список принимается
за исходный и процесс продолжается до тех пор,
пока все элементы не будут выбраны.
Очевидно, что выбранные элементы образуют
упорядоченный список.

13.

Сортировка выбором (пример)
Задача – упорядочить массив:
{5, 11, 6, 4, 9, 2, 15, 7}
Требуется найти минимальный элемент списка:
{2} {5, 11, 6, 4, 9, 15, 7}
{2, 4} {5, 11, 6, 9, 15, 7}
{2, 4, 5} {11, 6, 9, 15, 7}
*************************
{2, 4, 5, 6, 7, 9, 11,} {15}
{2, 4, 5, 6, 7, 9, 11,15}
Сложность алгоритма: O(n2)

14.

Простая сортировка вставкой
Алгоритм заключается в том что, на каждом
шаге
алгоритма
берется
один
из
неотсортированных
элементов
массива,
находится позиция для вставки среди
отсортированных и происходит вставка.
Gif - https://habr.com/ru/post/415935/

15.

Простая сортировка вставкой (пример)
Заданная неупорядоченная
последовательность элементов:
{40, 11, 83, 57, 32, 21, 75, 64}.
Сложность алгоритма: O(n2)

16.

Бинарная сортировка вставкой
При использовании метода сортировки вставками ключ i-го элемента сравнивается
приблизительно с i/2 ключами уже отсортированных элементов. Процесс можно ускорить,
используя метод бинарных вставок, т.е. сравнивать ключ i-го элемента (Ki) с ключом середины
уже отсортированной последовательности (Ki /2).
Затем в зависимости от того, ключ Ki меньше или больше Ki /2, будем рассматривать следующие
элементы: K1; Ki /2–1] или [Ki /2 + 1; Ki].
Для решения проблемы нечетного числа элементов множества номер центрального элемента
вычисляется по формуле: mid: = (low + high) div 2.
Сложность алгоритма: O(n2)
Gif - https://habr.com/ru/post/415935/

17.

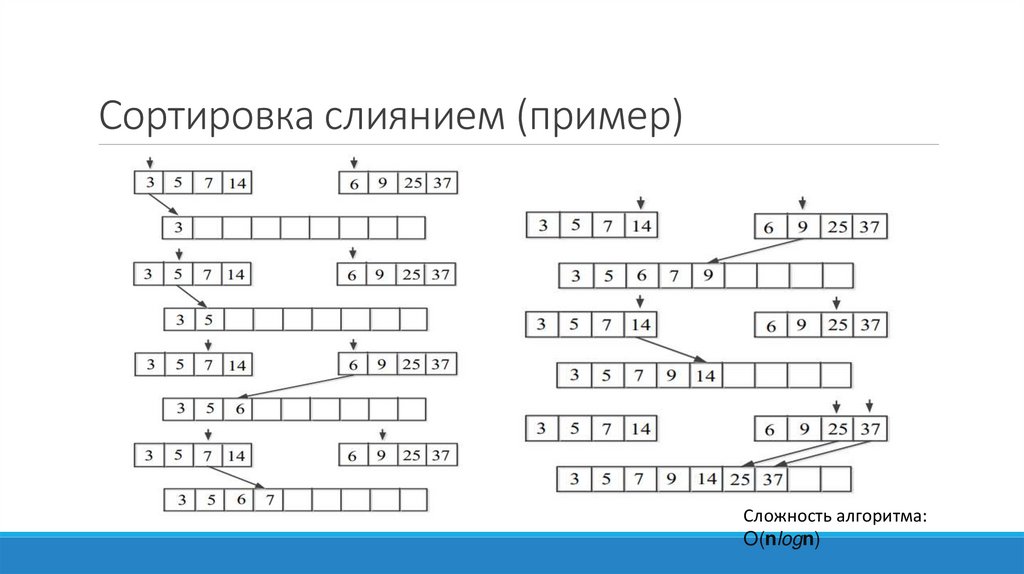
Сортировка слиянием (метод фон Неймана)
Используется для двух массивов.
Сначала анализируются первые элементы обоих
массивов. Меньший элемент переписывается в новый
массив.
Оставшийся элемент последовательно сравнивается с
элементами из другого массива. В новый массив после
каждого сравнения попадает меньший элемент.
Процесс продолжается до исчерпания элементов
одного из массивов. Затем остаток другого массива
дописывается в новый массив. Полученный новый
массив упорядочен таким же образом, как исходные.

18.

Сортировка слиянием (пример)
Сложность алгоритма:
O(nlogn)

19.

Сортировка обменом (метод пузырька)
В сортировке обменом элементы
списка
последовательно
сравниваются между собой и
меняются местами в том случае, если
предшествующий элемент больше
последующего.
Вариант 1
Вариант 2
Gif - https://habr.com/ru/post/415935/

20.

Сортировка обменом (пример)
Провести сортировку списка методом стандартного обмена или методом «пузырька» :
{40, 11, 83, 57, 32, 21, 75, 64}
Исходный список
40
11
11
40
83
57
32
21
75
64
Исходный список
11
40
11
40
57
83
32
Первый просмотр
75
64
21
75
57
57
83
64
75
64
83
64
32
57
21
83
75
57
32
Второй просмотр
21
40
21
57
83
11
32
40
40
Полученный список
57
83
Полученный список
11
40
32
21
57
75
64
Условие Айверсона: если в ходе сортировки при сравнении
элементов не было сделано ни одной перестановки, то
множество считается упорядоченным
Сложность алгоритма: O(n2)

21.

Шейкерная сортировка
Начинается
процесс
как
в
«пузырьке»:
максимальный
элемент отправляется в конец
массива. После этого процесс
идет в обратную сторону, при
этом
уже
выбирается
минимальный элемент, который
отправляется в начало массива.
Процесс продолжается тудаобратно несколько раз, в итоге
заканчивается
процесс,
оказавшись в середине списка.
Сложность алгоритма: O(n2)

22.

Сортировка Шелла
В методе Шелла сравниваются не
соседние элементы, а элементы,
расположенные на расстоянии d
(d – шаг между сравниваемыми
элементами)
d = [n/2], где
квадратные скобки обозначают,
что при делении берётся только
целая
часть
(округление
в
меньшую сторону).
После каждого просмотра шаг d
уменьшается вдвое. На последнем
просмотре он сокращается до d =
1.

23.

Сортировка Шелла (пример)
Имеется массив:
{40, 11, 83, 57, 32, 21, 75, 64}
Список длины n разбивается на n/2
частей, т.е. d = [n/2] = 4.
Шаг d = 4
Исходный массив
40
11
83
57
32
21
75
64
32
40
Шаг d = 4
11
21
75
83
57
Полученный массив
32
11
75
57
64
40
21
83
64

24.

Сортировка Шелла (пример-продолжение)
Шаг d = 2
Исходный массив
32
11
75
Шаг d = 1
57
40
21
83
64
Исходный список
32
32
11
11
32
32
75
40
21
75
57
64
40
Шаг d = 2
11
57
21
40
40
75
40
Шаг d =1
21
75
57
57
75
75
83
75
57
Полученный массив
83
83
64
64
32
11
40
21
75
57
83
64
Полученный список
Сложность алгоритма: O(n2)
11
32
21
40
57
75
64
83