Доска Гальтона

1. Доска Гальтона

ПОДГОТОВИЛ
СТУДЕНТ КУРСА М-11/19Д
СОЛЯНИК ЯРОСЛАВ ЮРЬЕВИЧ

2. Кто такой Гальтон?

16 февраля 1822 г.- 17 января 1911 г.
Френсис Гальтон - Английский
исследователь, географ, антрополог,
психолог, статистик, основатель
дифференциальной психологии и
психометрики, а также
основоположник евгеники.

3. Известное изобретение-Доска Гальтона

4. Что это такое?

Устройство, изобретённое
английским учёным Фрэнсисом
Гальтоном (первый экземпляр
изготовлен в 1873 году, затем
устройство было описано Гальтоном
в книге Natural inheritance, изданной в
1889 году) и предназначающееся для
демонстрации центральной
предельной теоремы, нормального
(гауссова) распределения.

5. Она состоит из:

Колышки
Канальцы
Шарики

6. Как работает доска?

1. Шарик попадает в первый колышек, и с
шансом 50 на 50 отскакивают к
следующим колышкам, что по диагонали
ниже.
2. Этапы продолжаются до того момента,
пока не достигнет канала.
3. Формирование кривой.

7. Чем обусловлен 3 пункт?

Так как отскок налево и направо
одинаково вероятен, на
длительной дистанции при
большом количестве испытаний,
можно предположить, что
шарики, чей путь содержит
одинаковое число отскоков
налево и направо будет
большинство, это означает, что
шарик закончит свой путь +- под
точкой старта, и гораздо меньше
по краям, что соответствует
отскокам в одном направлении.

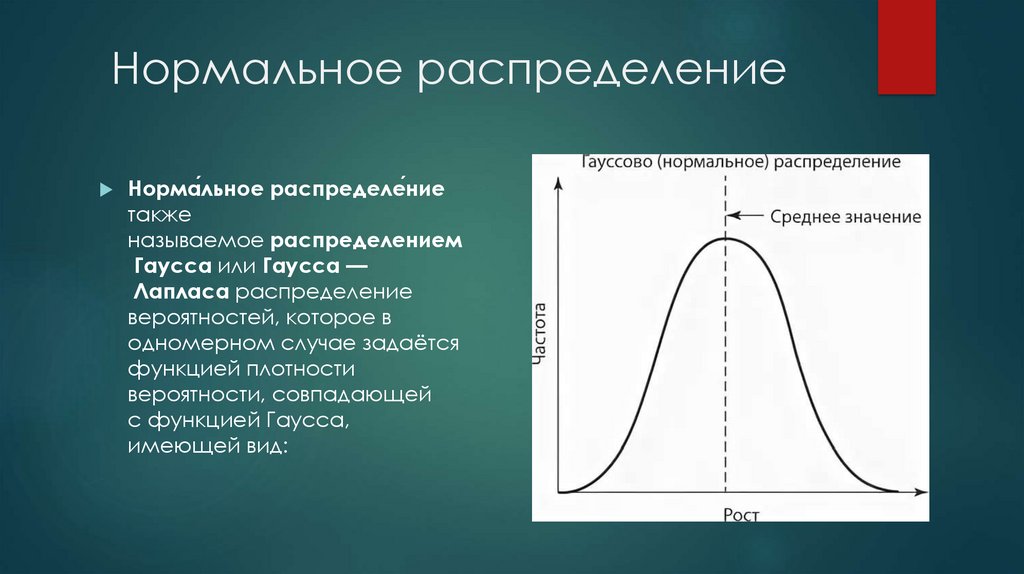
8. Нормальное распределение

Норма́льное распределе́ние
также
называемое распределением
Гаусса или Гаусса —
Лапласа распределение
вероятностей, которое в
одномерном случае задаётся
функцией плотности
вероятности, совпадающей
с функцией Гаусса,
имеющей вид:

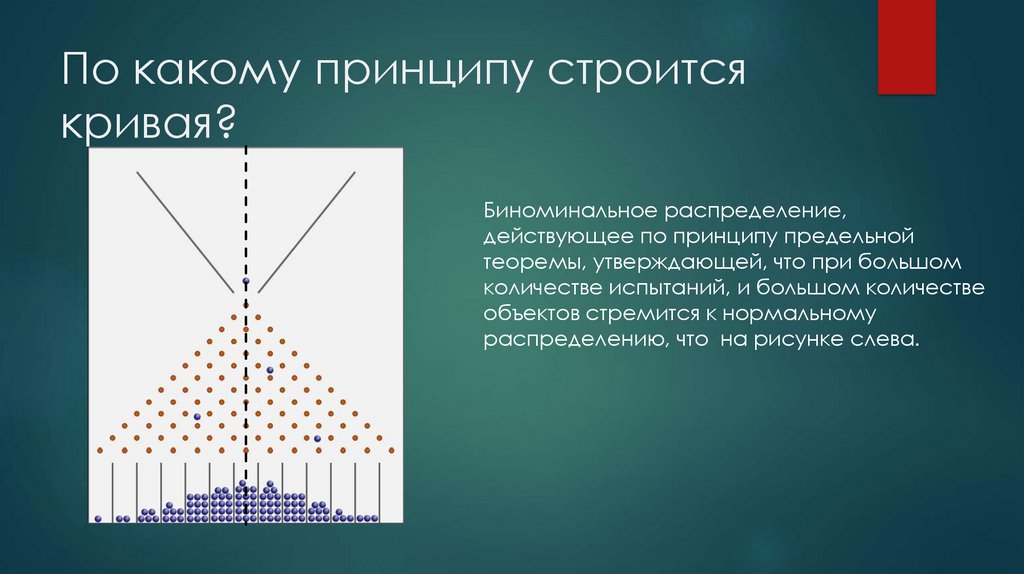
9. По какому принципу строится кривая?

Биноминальное распределение,
действующее по принципу предельной
теоремы, утверждающей, что при большом
количестве испытаний, и большом количестве
объектов стремится к нормальному
распределению, что на рисунке слева.

10. Треугольник Паскаля

- Бесконечная таблица биномиальных
коэффициентов, имеющая треугольную
форму. В этом треугольнике на вершине и
по бокам стоят единицы. Каждое число
равно сумме двух расположенных над ним
чисел.
Число над колышком говорит о том, сколько
путей для достижения цели есть в данной точке.

11. Где применяется доска?

Шашки
Игровой автомат «Патинко»
Если посмотреть, то работает тот же
принцип

12. Выводы:

Доска Гальтона подтвержает нормальное распределение
Треугольник Паскаля совпадающий с колышками, показывает
то, какое количество «испытаний» прошел шарик
Доска нашла применение в игровых и настольных играх
В большинстве случаев шарики в каналах +- совпадают с кривой
Гаусса, но всегда в центре больше, чем на краях.

13. Источники:

https://www.youtube.com/watch?v=JScmzAVxoRA&t=301s
https://pikabu.ru/story/doska_galtona__nastoyashchaya_magiya_te
oriya_veroyatnosti_5889061
https://ru.wikipedia.org/wiki/Нормальное_распределение
https://nauka.club/matematika/treugolnik-paskalya.html