Импульсные и цифровые устройства

1.

2.

Общие сведения
Кроме напряжения синусоидальной формы в практике электротехники и
электроники применяются напряжения других форм. Наиболее широко применяется
импульсное напряжение.
Импульсным называется прерывистое во времени напряжение (сигнал) любой
формы.
Под формой сигнала понимается закон изменения во времени напряжения или
тока.
Широкое применение импульсных сигналов обусловлено рядом причин:
– сочетанием импульсов и пауз легко передавать дискретную
информацию;
– импульсный сигнал оказался единственно приемлемой формой при
создании радиолокации;
– необходим для работы систем синхронизации;
– удобен для управления многими производственными процессами;
– наличие пауз между импульсами позволяет уменьшить мощность,
потребляемую от источника питания;
– во время паузы можно передавать информацию от других.

3.

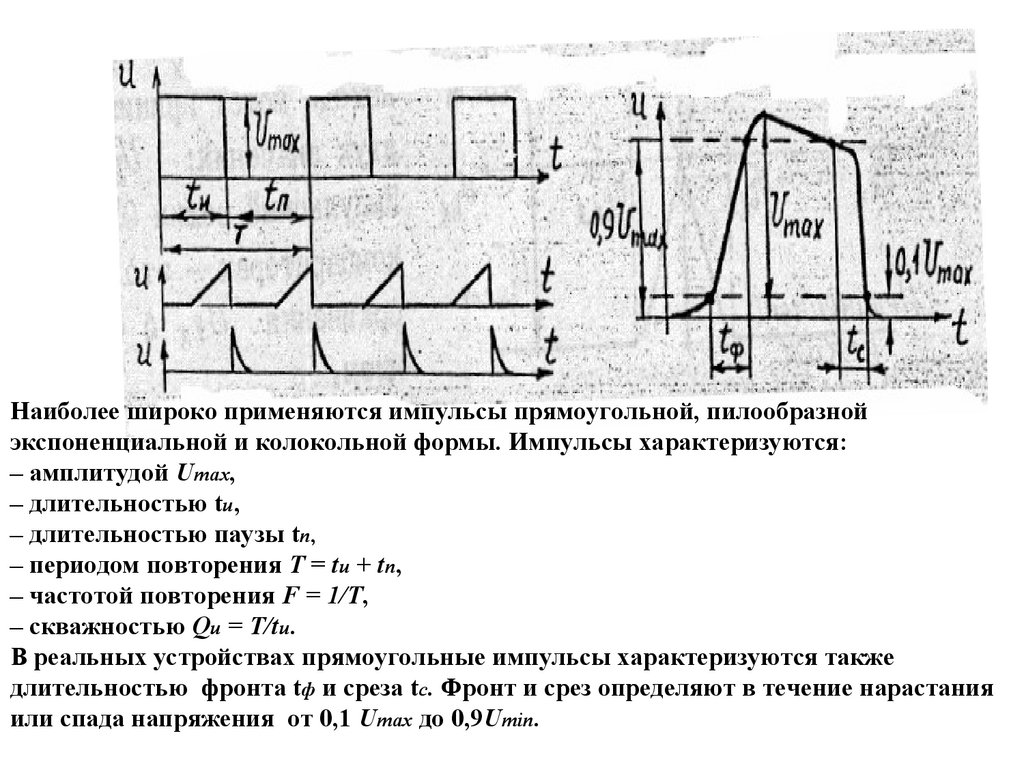
Наиболее широко применяются импульсы прямоугольной, пилообразной
экспоненциальной и колокольной формы. Импульсы характеризуются:
– амплитудой Umах,
– длительностью tи,
– длительностью паузы tп,
– периодом повторения Т = tи + tn,
– частотой повторения F = 1/T,
– скважностью Qu = T/tu.
В реальных устройствах прямоугольные импульсы характеризуются также
длительностью фронта tф и среза tс. Фронт и срез определяют в течение нарастания
или спада напряжения от 0,1 Umах до 0,9Umin.

4.

Устройства, выполняющие обработку импульсных сигналов, называются
импульсными устройствами.
Среди различных импульсных устройств видное место занимают
электронные ключи.
Через идеальный разомкнутый ключ ток не протекает.
Напряжение на идеальном замкнутом ключе равно нулю.
Смена состояния ключа происходит под действием сигналов, подаваемых на
один или несколько входов.
Наиболее широкое применение в качестве электронных ключей нашел
транзисторный каскад по схеме с ОЭ в ключевом режиме.

5.

В семействе выходных характеристик проводим ВАХ резистора RК, удовлетворяющую
уравнению:
U КЭ E K RK K
. Этот график называют статической линией нагрузки и строят по двум точкам.
+EK
Rк
iвх
Uвх
Rб
EK
RK
IK
IK2
А2
I”б> I’б
I’б>0
VT
Uбэ
Uкэ
А1
IK1
Uвых
0
Uкэ2
Uкэ1
Iб=0
EK
Uкэ
1) Режим отсечки (точка А1) Этот режим реализуется при отрицательном смещении базы UБЭ < 0 , ІБ = 0
(транзистор закрыт);
.,.2) режим насыщения (точка А2), когда транзистор открыт:
Переход из режима отсечки в режим насыщения осуществляется подачей Uвх > 0. При этом повышению Uвх
соответствует понижение Uвых. Поэтому ключ называют инвертирующим.

6.

7.

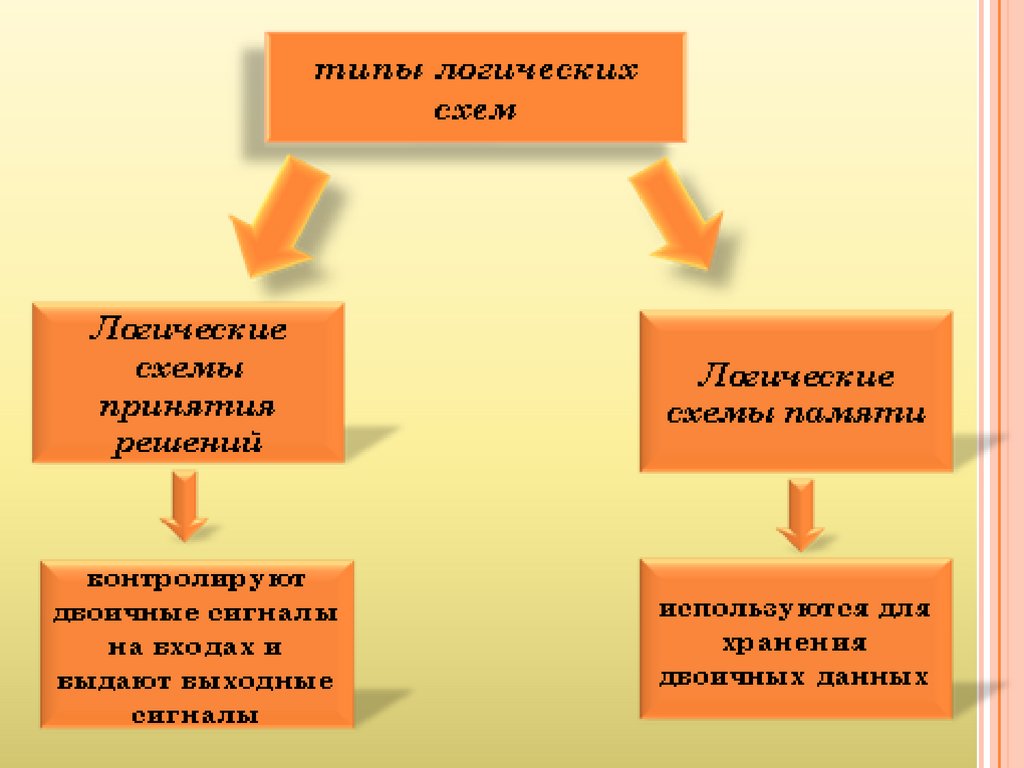
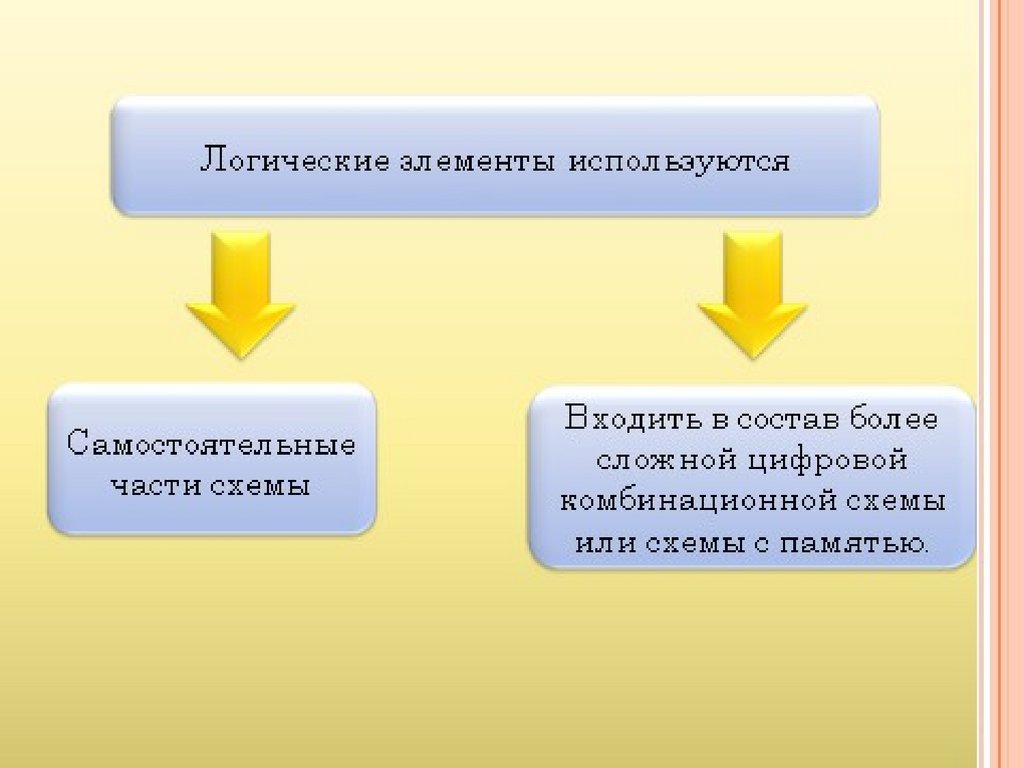
Основой построения любого устройства, использующего цифровую информацию, являются
элементы двух типов: логические и запоминающие. Логические элементы выполняют простейшие
логические операции над цифровыми сигналами. Запоминающие элементы служат для хранения
цифровой информации (состояния разрядов кодовой комбинации).
Логическая операция состоит в преобразовании по определенным правилам входных цифровых
сигналов в выходные. Математически цифровые сигналы обозначают поразрядно символами,
например, x1, x2, x3, x4. Их называют переменными. Каждая переменная может принимать значение "0" или
"1". Результат логической операции часто обозначают F или Q. Он также может иметь значение "0" или "1".
Взаимосвязь переменных образуют логическую функцию F = f(x). Так как аргумент принимает конечное
значение, а именно (1 или 0), то число возможных логических функций всегда конечно и равно:
где –
число наборов логических переменных, n – число независимых переменных.
m
N 2 одной переменной F = f(x) n = 1; m = 2; N = 4, т. е. существуют четыре варианта
Для функции
m 2n
функции:
x
FI FII FIII
FIV
0
0
0
1
1
1
0
1
0
1
FI - нулевая функция; FII – функция повторения; FIII - инверсия;FIV – единичная функция.
Математическим аппаратом логики является алгебра Буля. В булевой алгебре над переменными "0" или "1"
могут выполняться три основных действия:
логическое сложение, логическое умножение и логическое отрицание

8.

9.

10.

11.

12.

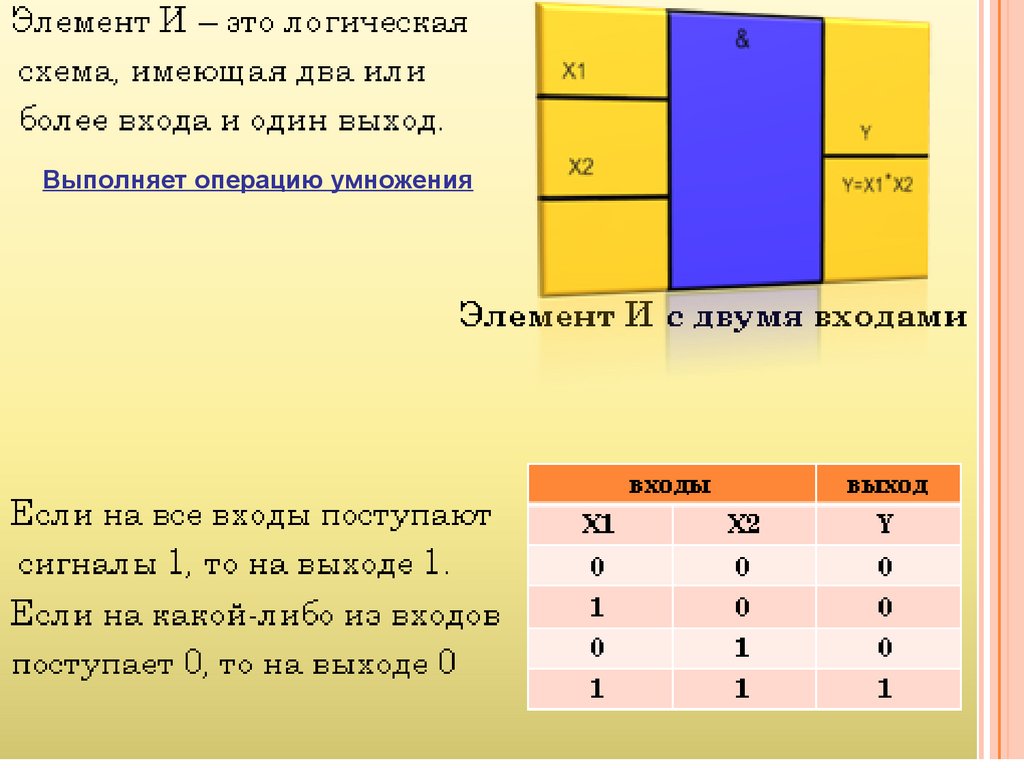
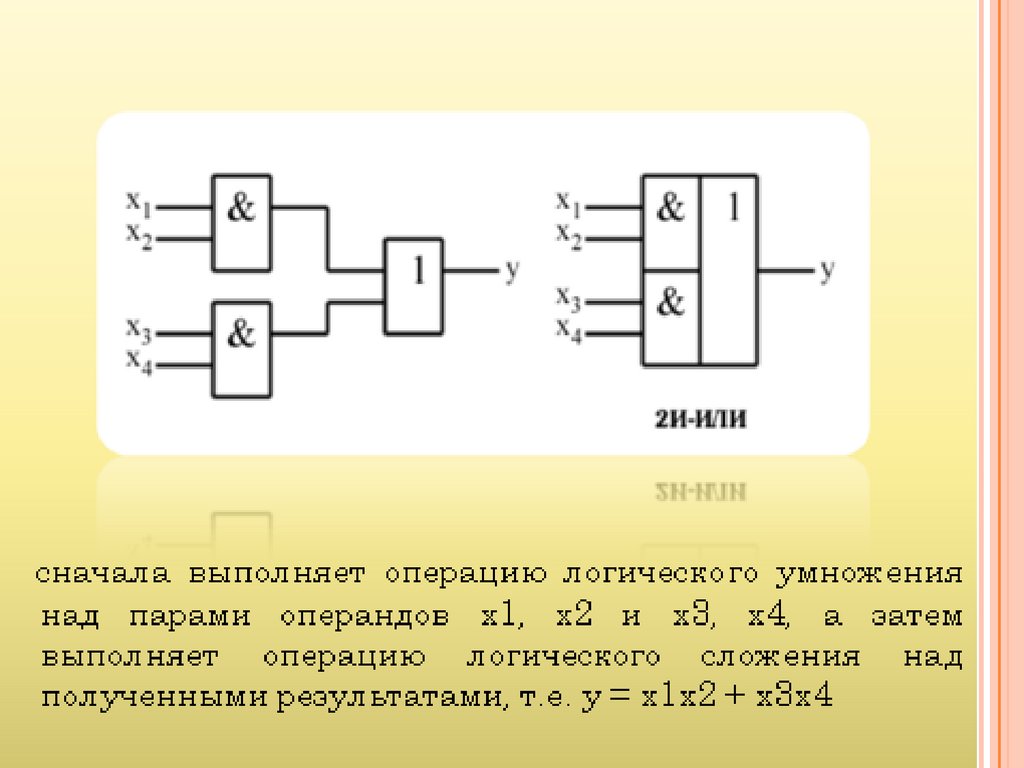
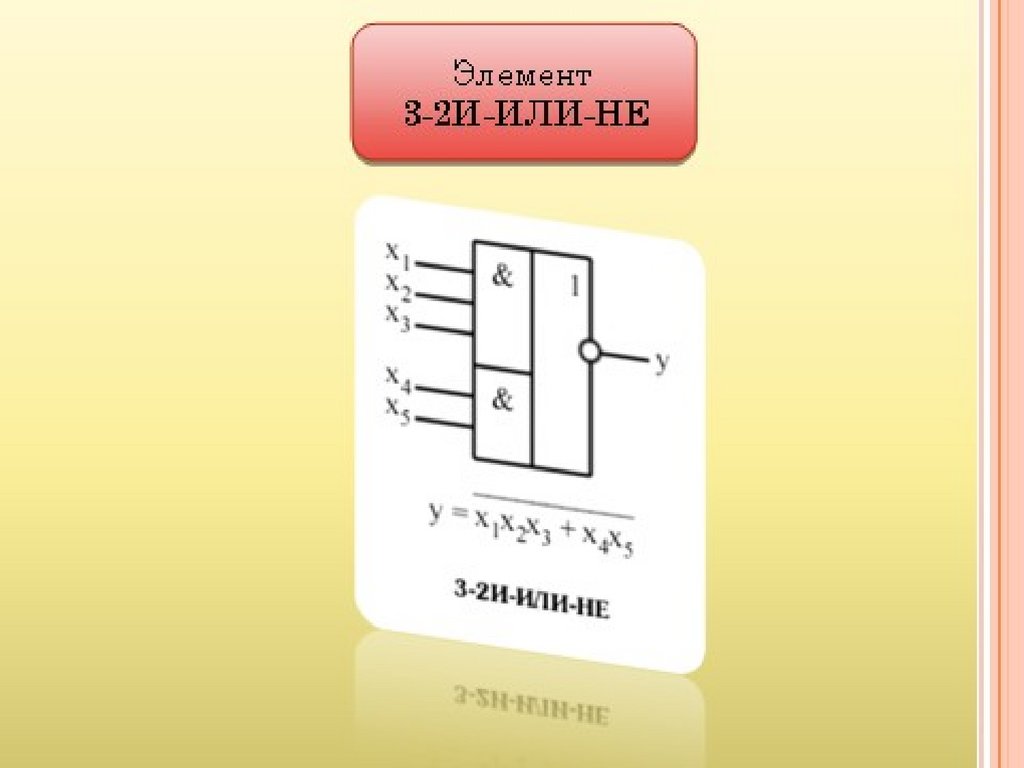
Выполняет операцию умножения

13.

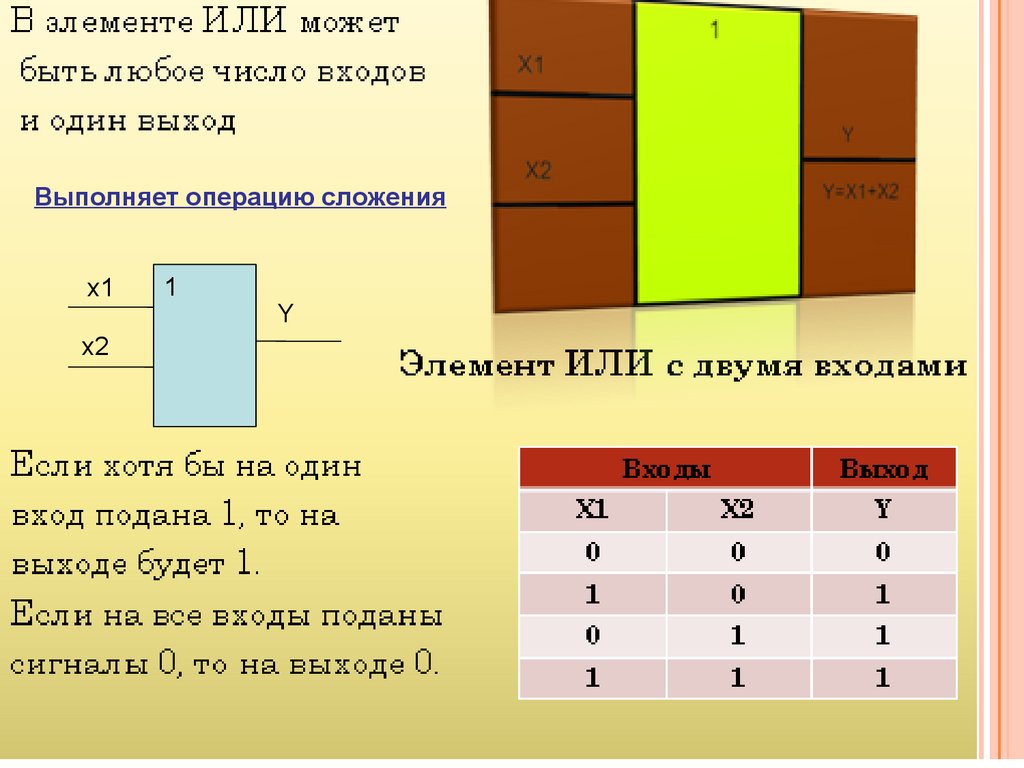
Выполняет операцию сложения
х1
х2
1
Y

14.

15.

16.

17.

18.

19.

20.

1

21.

22.

23.

24.

25.

26.

27.

28.

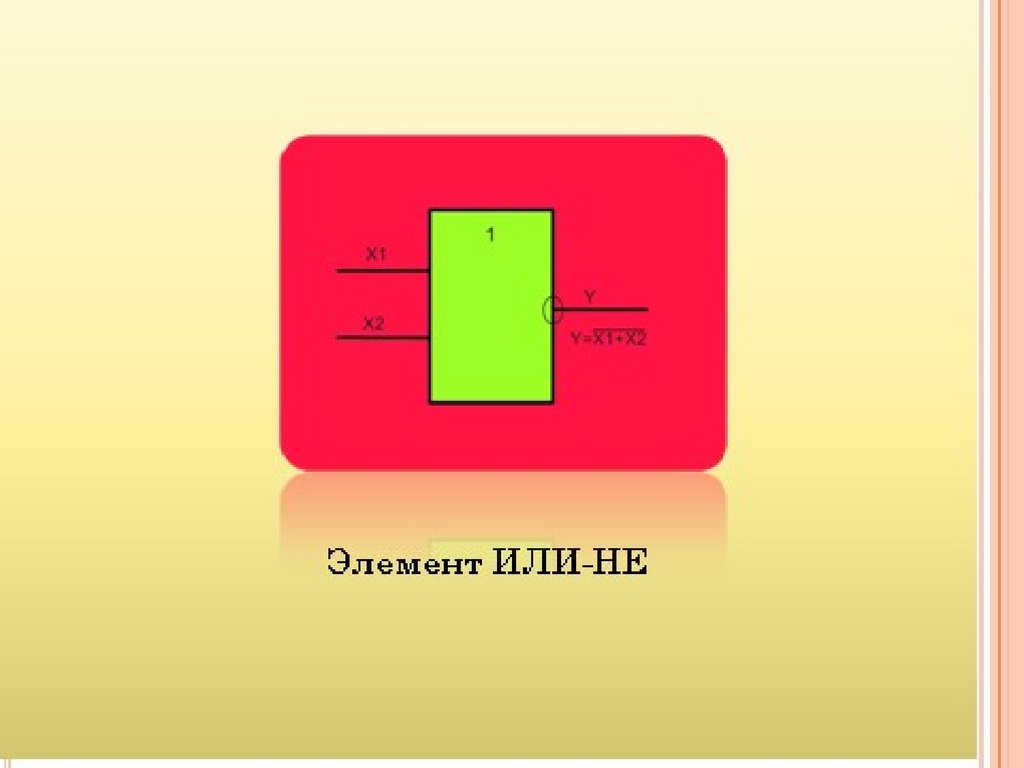
Логическое сложение (дизъюнкция или операция ИЛИ) записывается в виде
F x1 x2 ... xn .
Правила выполнения операции ИЛИ заключаются в следующем:
Х1 Х2 F
0 + 0 = 0;
0 + 1 = 1;
Х1 Х2 F
1 + 0 = 1;
1 + 1 = 1.
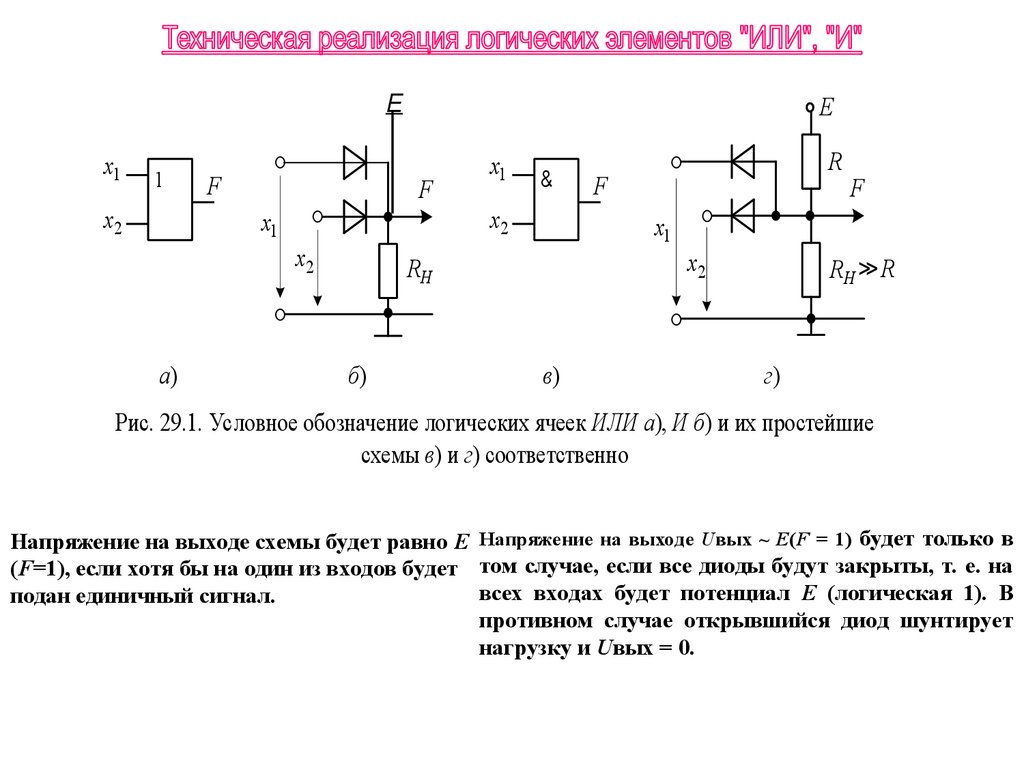
Логические схемы, реализующие операцию ИЛИ, называют ячейками ИЛИ.
Простейшая реализация логической ячейки ИЛИ осуществляется на диодах
Логическое умножение (конъюнкция или операция И) записывается в виде
F x1 x2 ... xn .
Правила выполнения операции И заключаются в следующем:
Х1 Х2 F
Х1 Х2 F
0 · 0 = 0;
1 · 0 = 0;
0 · 1 = 0;
1 · 1 = 1.
Логические схемы, реализующие операцию И, называются ячейками И. Простейшая
реализация логической ячейки И осуществляется на диодах.

29.

Е
x1
1
x2
F
E
F
&
x2
x1
x2
а)
x1
F
F
x1
x2
RH
б)
R
в)
RH R
г)
Рис. 29.1. Условное обозначение логических ячеек ИЛИ а), И б) и их простейшие
схемы в) и г) соответственно
Напряжение на выходе схемы будет равно E Напряжение на выходе Uвых ~ Е(F = 1) будет только в
(F=1), если хотя бы на один из входов будет том случае, если все диоды будут закрыты, т. е. на
всех входах будет потенциал Е (логическая 1). В
подан единичный сигнал.
противном случае открывшийся диод шунтирует
нагрузку и Uвых = 0.

30.

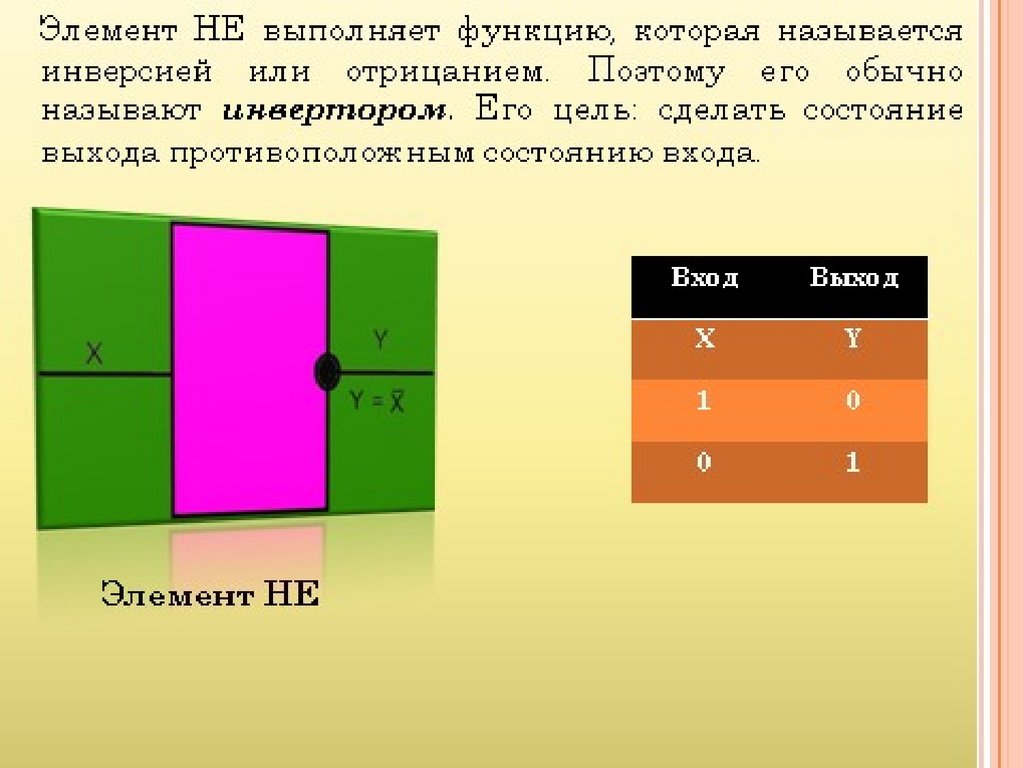
Логическое отрицание (инверсия или операция НЕ) записывается в виде
F x
и читается: F равно не x. Правила выполнения операции НЕ заключаются в
следующем:
0 1;
0 0;
1 0реализующие
;
Логические схемы,
операцию
1 называются
1.
ячейками НЕ. Операция НЕ может быть реализована
схемой
транзисторного ключа
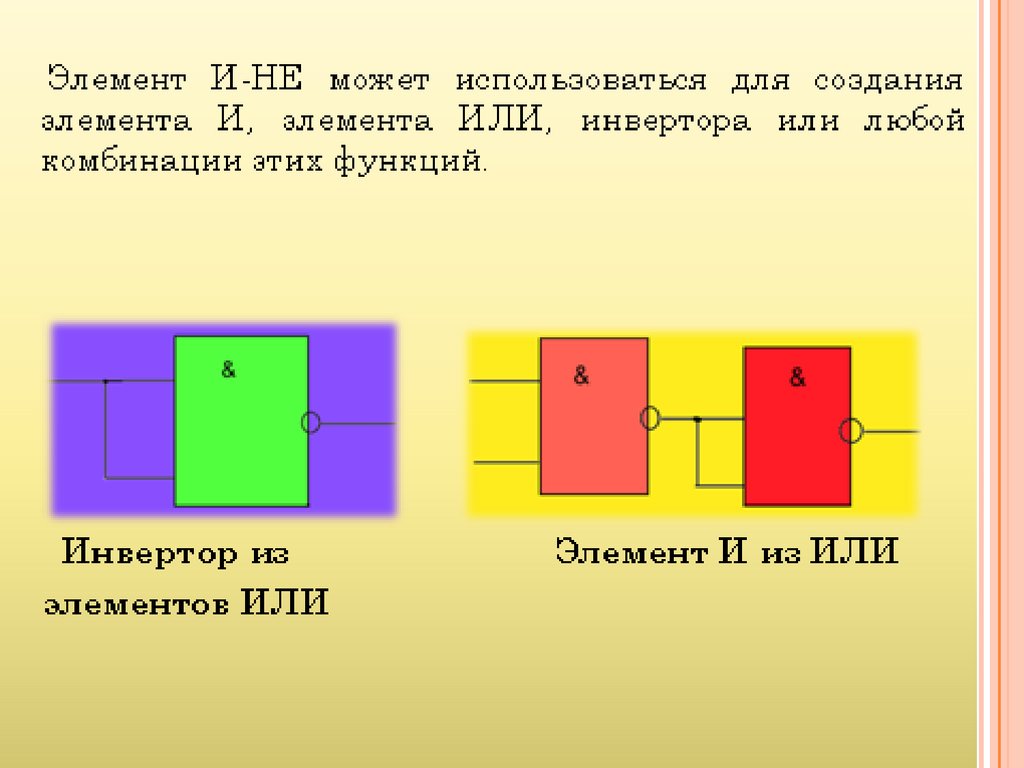
Рассмотренные логические операции и схемы позволяют реализовать сколь угодно сложную логическую
F x1 x2 x1 x 2
функцию.
реализуется
пятью
логическими
элементами, в том числе два элемента И, два элемента НЕ и один элемент ИЛИ
Например, функция
E
RK
1
x
Rб
x1
1
&
x
x2
1
1
F
&
в)
а)
б)
Рис. 29.2. Условное обозначение а), простейшая схема логической ячейки НЕ б)
и пример реализации логической функции в)
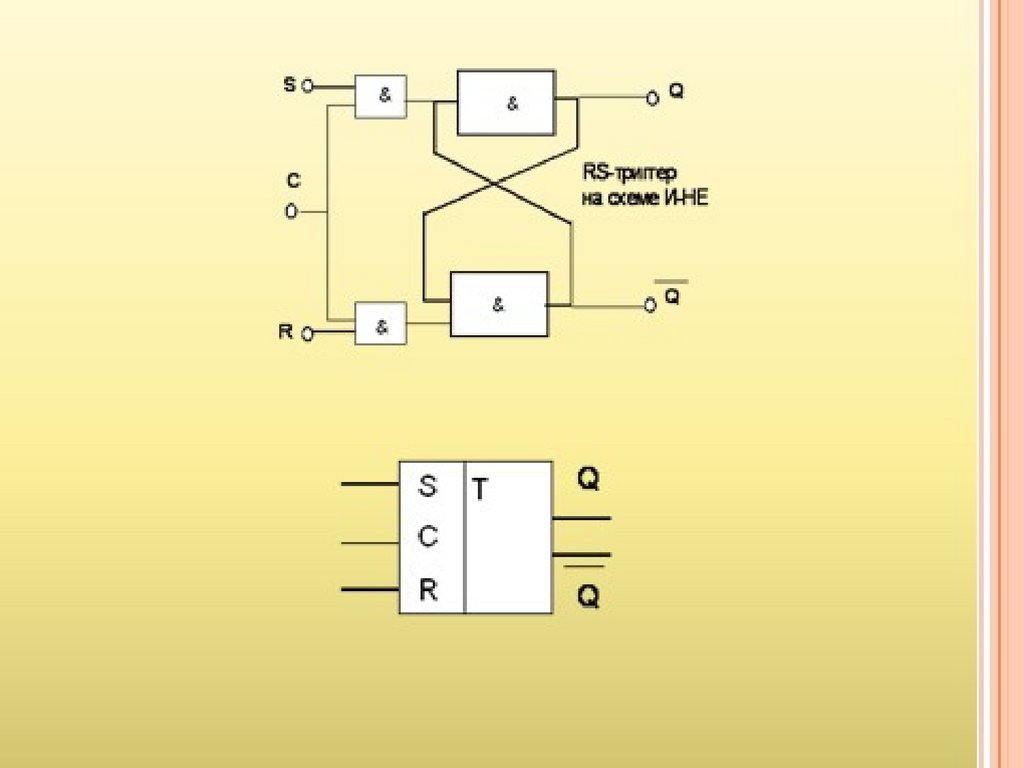
Все логические элементы выпускаются в микросхемном исполнении.