Схемотехника цифровых устройств. Лабораторные занятия

1.

Схемотехника
цифровых
устройств
ч.1

2.

Лекции
Лабораторные
занятия
Практические занятия
Академ. часов на курс.
работу (проект)
Контрольные работы
Форма
текущей
аттестации
Всего
Аудиторных
часов
Семестр
Название
специальности специальности
Курс
Код
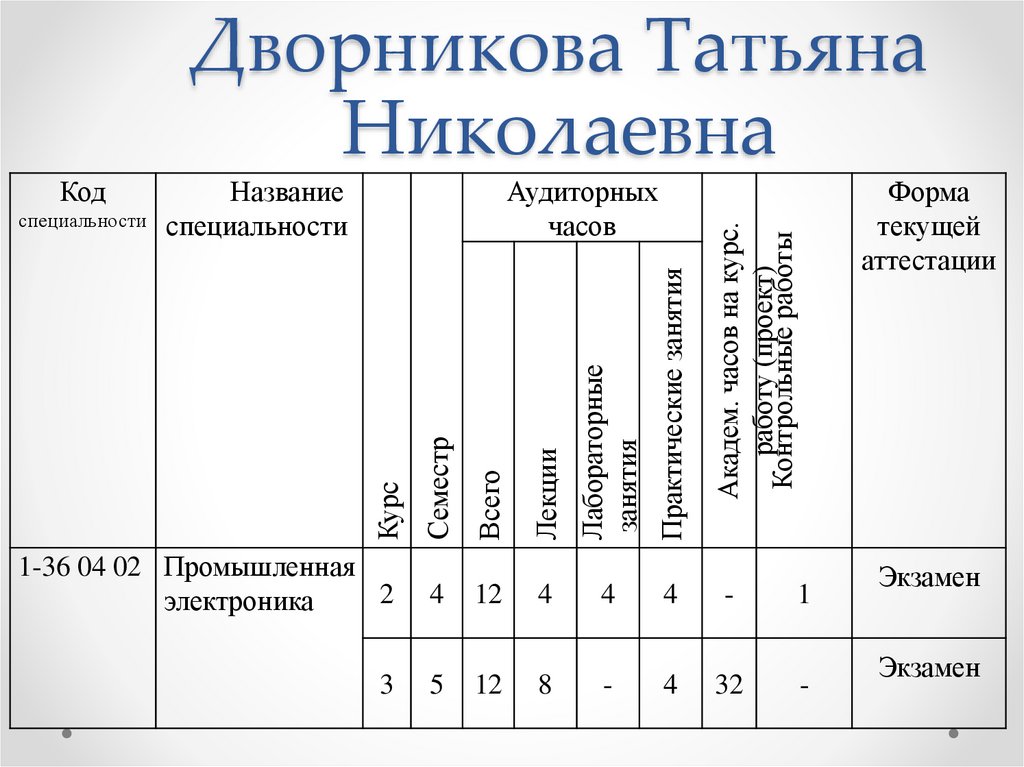
Дворникова Татьяна
Николаевна
1-36 04 02 Промышленная
2
электроника
4
12
4
4
4
-
1
3
5
12
8
-
4
32
-
Экзамен
Экзамен

3.

литература
•1. Опадчий, Ю. Ф. Аналоговая и цифровая электроника: учебник для
вузов / Ю. Ф. Опадчий, О. П. Глудкин, А. И. Гуров. – М.: Горячая линия
– Телеком, 2005. – 768 с.
•2. Безуглов, Д. А. Цифровые устройства и микропроцессоры:
учебное пособие для вузов / Д. А. Безуглов, И. В. Калиенко. – Ростов
н/Д: Феникс, 2008. – 468 с.
•3. Браммер, Ю. А. Цифровые устройства: учебное пособие для вузов /
Ю. А. Браммер, И. Н. Пащук. – М.: Высш. шк., 2004. – 229 с.
•4. Калабеков,
Б.А. Цифровые устройства и микропроцессорные
системы: учебник для сузов. – М.: Горячая линия – Телеком, 2002. – 336
с.
• 5. Гусев, В.Г. Электроника и микропроцессорная техника: учебник
для вузов. – М.: Высш.шк., 2004 – 790 с.
• 6. Цифровые устройства. Лабораторный практикум: учеб.- метод.
пособие / Р. Г. Ходасевич, В. Н. Левкович, А. В. Мартинович, Е. Н.
Каленкович. – Минск: БГУИР, 2010. – 112 с.: ил.
•7. Будько, А. А. Цифровые устройства. Технология IDL : учеб.-метод.
пособие / А. А. Будько. – Минск : БГУИР 2011. – 135 с.

4.

• 8. Нефедов, В. И. Основы радиоэлектроники и связи: учебник для вузов/
В.И. Нефедов – 2-е изд. – М.: Высш. шк., 2002. – 510 с.
• 9. Логические ИС КР1533, КР1554: справочник. В 2 ч. / И. И. Петровский
[и др.]. – М. : ТОО «БИНОМ», 1993. – 496 с.
• 10. ГОСТ 2.743–91. Элементы цифровой техники.
• 11. Уэйкерли, Дж. Проектирование цифровых устройств: в 2 т. / Дж.
Уэйкерли; пер. с англ. – М.: Постмаркет, 2002. – 1072 с.
• 12. Точчи, Р. Д. Цифровые системы. Теория и практика, 8-е изд. / Р. Д.
Точчи, Н. С. Уидмер; пер. с англ. – М. : Изд. дом «Вильямс», 2004. – 1024 с.
• 13. Хернитер, М. Е. Multisim. Современная система компьютерного
моделирования и анализа схем электронных устройств / Марк Е. Хернитер;
пер. с англ. – Изд. дом «ДМК-пресс», 2006. – 488 с.
• 14. Нефедов А. В. Интегральные микросхемы и их зарубежные аналоги:
Справочник / А. В. Нефедов. В 12-ти томах. – М.: ИП РадиоСофт, 2001.
15. Новожилов, О.П. Основы цифровой техники/ А.В. Новожилов – М.:
ИП РадиоСофт, 2004. – 528 с.
16.
Загидуллин,
Р.Ш.
Multisim,
LabVIEW.
Практика
автоматизированного проектирования электронных устройств/ Р.Ш.
Загидуллин – М.: Горячая линия – Телеком, 2009. – 336 с.: ил.

5.

Введение.
Позиционные системы
счисления

6.

вопросы
•Структура и содержание учебной дисциплины, ее связь с
другими дисциплинами учебного плана специальности. Задачи
дисциплины и ее роль в обеспечении базовой теоретической и
инженерной подготовкой специалиста по фундаментальным
основам
схемотехники
цифровых
устройств.
Основные
исторические этапы развития цифровой электроники.
Классификация радиотехнических сигналов. Принцип
аналого-цифрового преобразования информации. Основные
процессы
преобразования:
дискретизация,
квантование,
кодирование. Цифровые сигналы. Виды и параметры импульсных
сигналов.
•Позиционные системы счисления, используемые в цифровых
устройствах:
двоичная, восьмеричная, шестнадцатеричная,
двоично-десятичная. Преобразование чисел из одной системы
счисления
в
другую.
Арифметические
действия
над
многоразрядными двоичными числами. Методы кодирования
сигналов, применяемые в цифровых устройствах.

7.

1. Виды и параметры импульсных
сигналов.
Классификация радиотехнических сигналов
Сигналом называют физический процесс, несущий
информацию о состоянии какого-либо объекта
наблюдения.
В радиоэлектронике применяют в основном
электрические сигналы, у которых информация
сосредоточена в изменениях параметров физического
процесса - амплитуде, частоте, фазе и других
параметрах.

8.

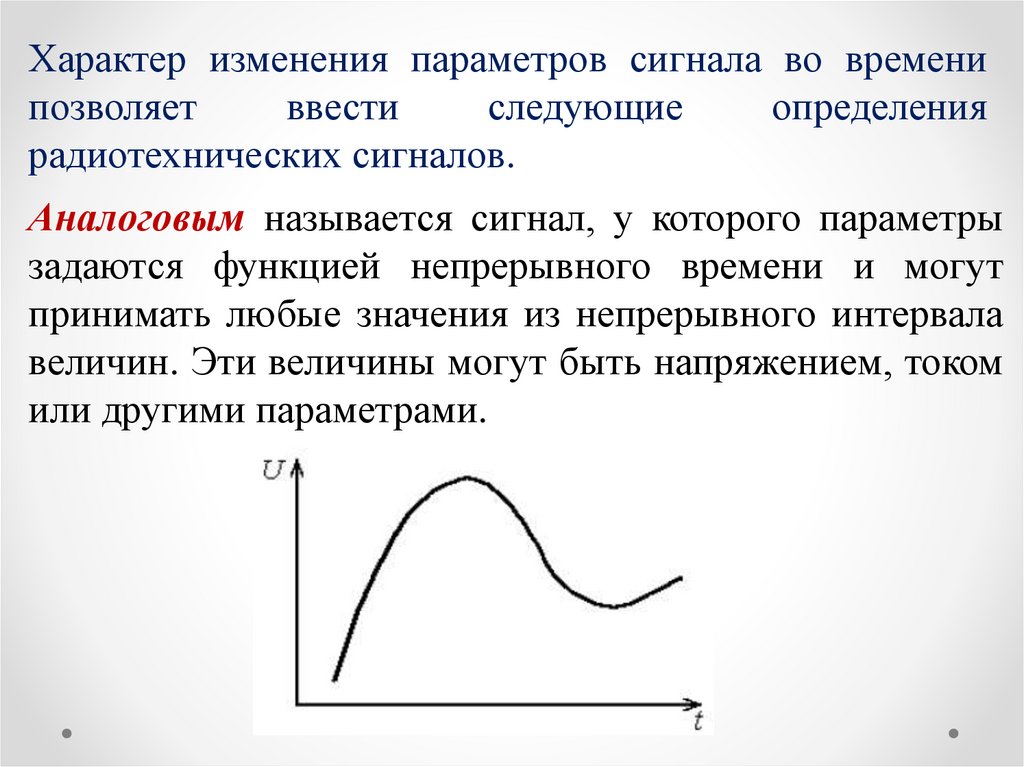
Характер изменения параметров сигнала во времени
позволяет
ввести
следующие
определения
радиотехнических сигналов.
Аналоговым называется сигнал, у которого параметры
задаются функцией непрерывного времени и могут
принимать любые значения из непрерывного интервала
величин. Эти величины могут быть напряжением, током
или другими параметрами.

9.

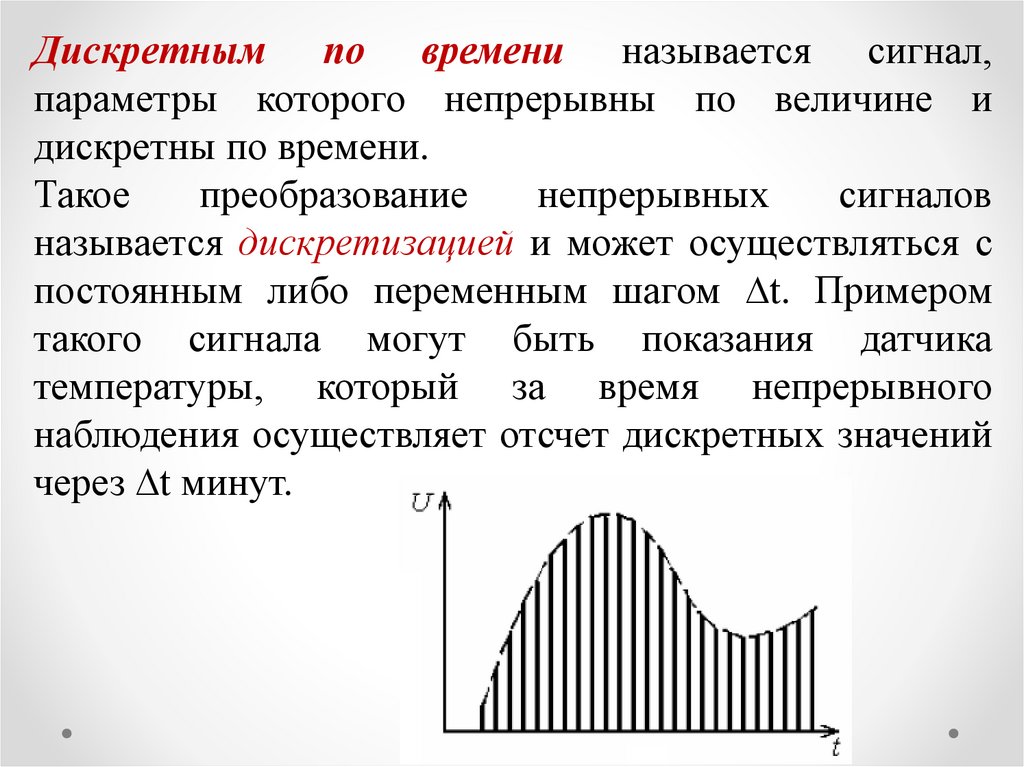
Дискретным по времени называется сигнал,
параметры которого непрерывны по величине и
дискретны по времени.
Такое
преобразование
непрерывных
сигналов
называется дискретизацией и может осуществляться с
постоянным либо переменным шагом ∆t. Примером
такого сигнала могут быть показания датчика
температуры, который за время непрерывного
наблюдения осуществляет отсчет дискретных значений
через ∆t минут.

10.

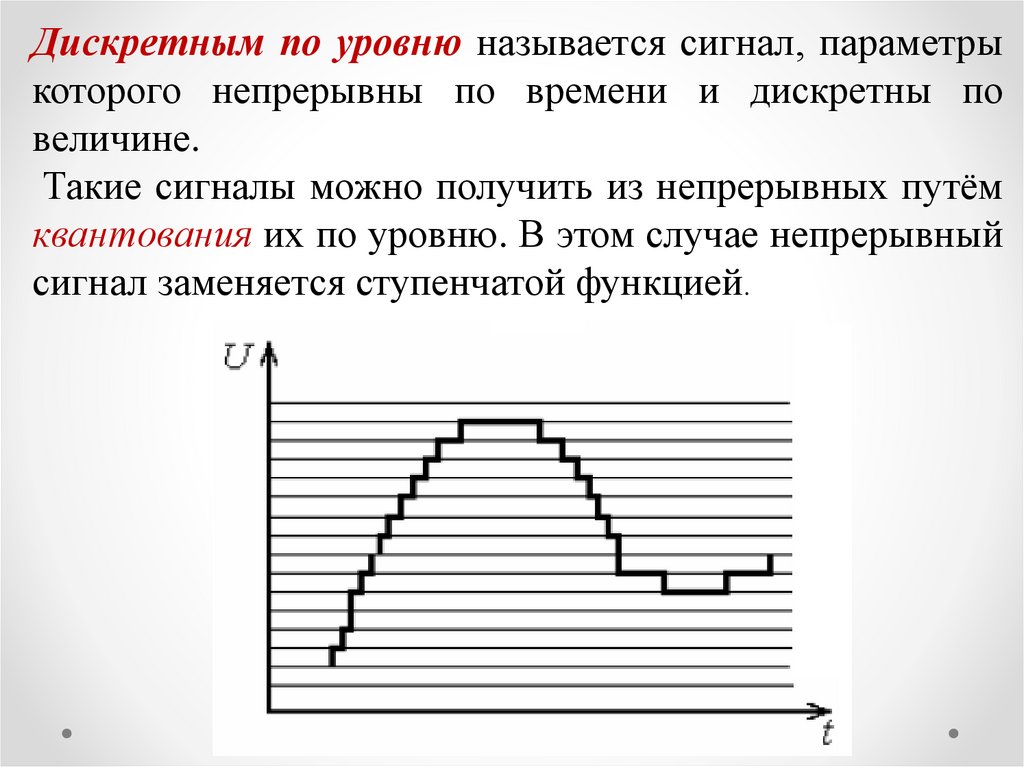
Дискретным по уровню называется сигнал, параметры
которого непрерывны по времени и дискретны по
величине.
Такие сигналы можно получить из непрерывных путём
квантования их по уровню. В этом случае непрерывный
сигнал заменяется ступенчатой функцией.

11.

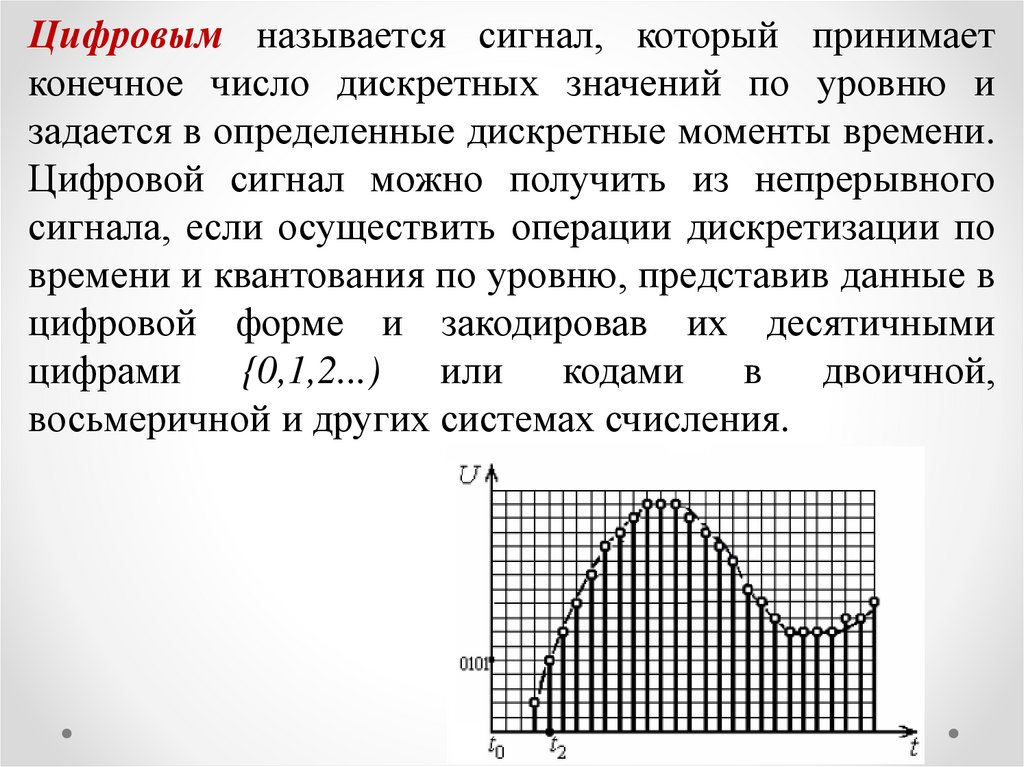
Цифровым называется сигнал, который принимает
конечное число дискретных значений по уровню и
задается в определенные дискретные моменты времени.
Цифровой сигнал можно получить из непрерывного
сигнала, если осуществить операции дискретизации по
времени и квантования по уровню, представив данные в
цифровой форме и закодировав их десятичными
цифрами {0,1,2...) или кодами в двоичной,
восьмеричной и других системах счисления.

12.

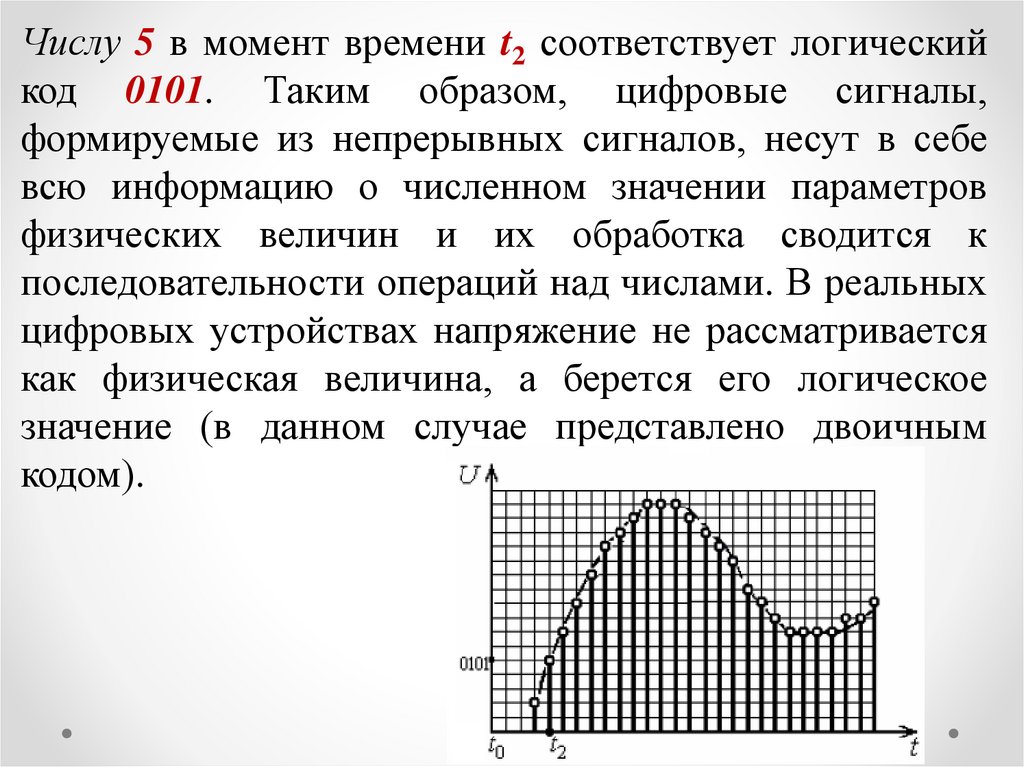
Числу 5 в момент времени t2 соответствует логический
код 0101. Таким образом, цифровые сигналы,
формируемые из непрерывных сигналов, несут в себе
всю информацию о численном значении параметров
физических величин и их обработка сводится к
последовательности операций над числами. В реальных
цифровых устройствах напряжение не рассматривается
как физическая величина, а берется его логическое
значение (в данном случае представлено двоичным
кодом).

13.

Цифровой сигнал – это сигнал, который может
принимать два (иногда три) значения, причем
разрешены некоторые отклонения от этих
значений.
Например, напряжение может
принимать два значения от 0 до 0,5 В (уровень
нуля) или от 2,5 до 5В (уровень единицы).
Цифровые
устройства – это устройства,
работающие исключительно с цифровыми
сигналами.

14.

Логические сигналы действуют в цифровых устройствах
наряду с цифровыми сигналами и характеризуют
наступление или не наступление того или иного
события. Логические сигналы обычно представляются
высоким (лог. 1) или низким (лог. 0) уровнем
потенциалов напряжения и относятся к классу
положительной логики. При обратном представлении
(лог. 1 - низкий уровень, лог. 0 - высокий) логические
сигналы относятся к классу отрицательной логики.
Применительно к логическим сигналам символы 1 и 0
являются информационными значениями сигналов
и
не характеризуют их реальные величины, они лишь
описывают качественное состояние события (событие
истинно или ложно), поэтому к логическим сигналам
неприменимы арифметические операции.

15.

Виды и параметры импульсных и цифровых
сигналов
В импульсных устройствах используются прерывистые
кратковременные электрические колебания (импульсы),
обусловленные отклонением напряжения или тока от
некоторого постоянного либо нулевого уровня.
Импульсные
колебания,
параметры
которых
изменяются
в
соответствии
с
передаваемой
информацией, называются импульсными сигналами.

16.

Такие сигналы являются аналоговыми, так как в
течение
ограниченного
интервала
времени,
соизмеримого со временем завершения переходного
процесса в схеме, они непрерывны и могут принимать в
диапазоне своих изменений любые значения.
Примером
импульсных
сигналов
являются
последовательности видео- и радиоимпульсов, которые
могут иметь различные виды импульсной и импульснокодовой модуляции (АИМ, ШИМ, ФИМ. ЧИМ).

17.

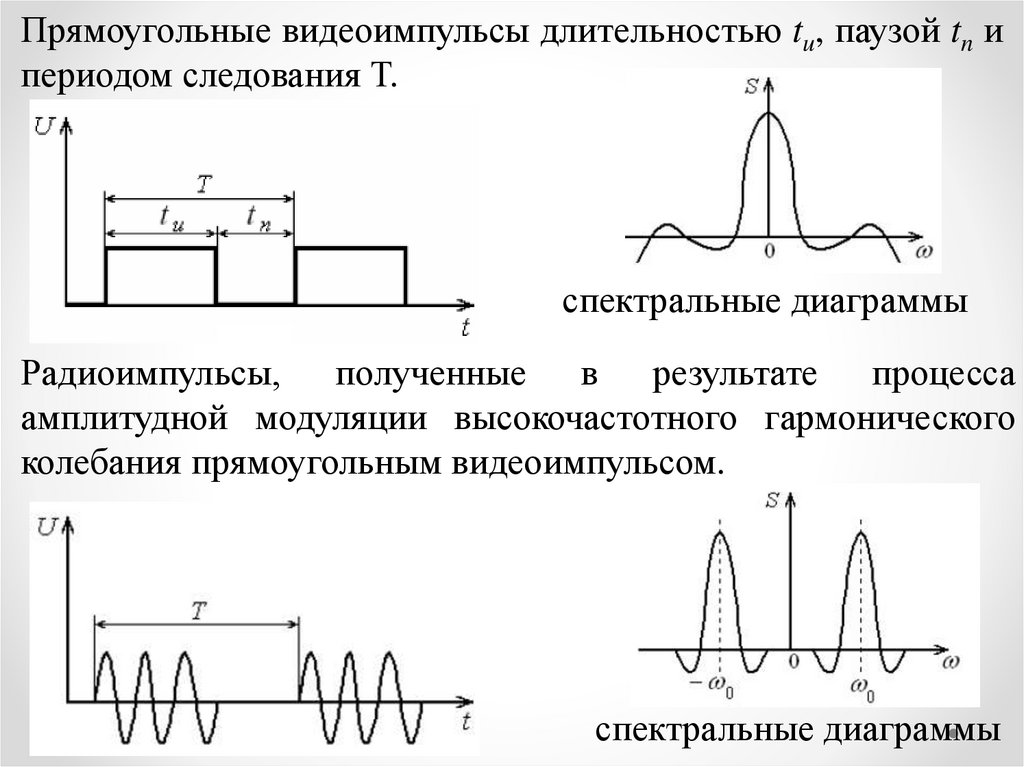
Прямоугольные видеоимпульсы длительностью tu, паузой tn и
периодом следования Т.
спектральные диаграммы
Радиоимпульсы, полученные в результате процесса
амплитудной модуляции высокочастотного гармонического
колебания прямоугольным видеоимпульсом.
спектральные диаграммы

18.

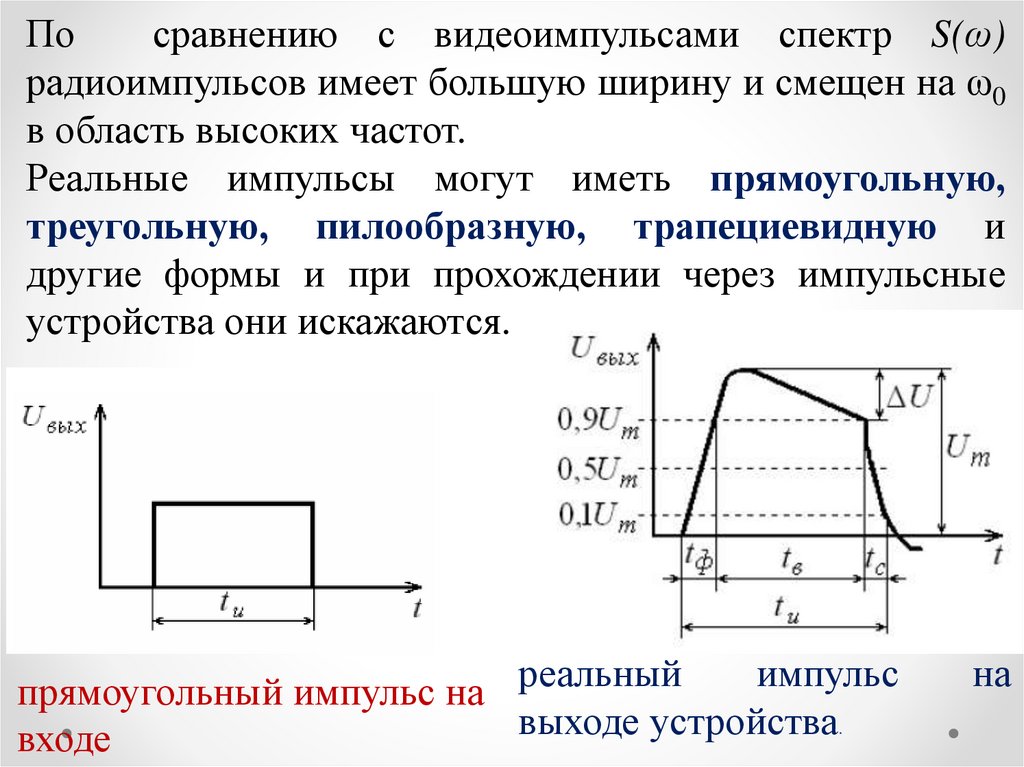
По
сравнению с видеоимпульсами спектр S(ω)
радиоимпульсов имеет большую ширину и смещен на ω0
в область высоких частот.
Реальные импульсы могут иметь прямоугольную,
треугольную, пилообразную, трапециевидную и
другие формы и при прохождении через импульсные
устройства они искажаются.
импульс
прямоугольный импульс на реальный
выходе устройства.
входе
на

19.

20.

Актуальность цифровых методов формирования
сигналов и обработки информации
1. Аналоговые сигналы непрерывны и могут
быть определены в любой момент времени, в то
время как цифровые сигналы могут быть
определены в дискретные (выделенные) моменты
времени. Поэтому быстродействие аналоговых
устройств принципиально выше, чем цифровых.
Однако аналоговая техника в настоящее время
достаточно близко подошла к пределу своих
возможностей по массогабаритным и другим
характеристикам.

21.

2. Цифровая обработка сигналов обладает рядом
существенных преимуществ:
•огромная степень интеграции;
•малая зависимость от параметров окружающей
среды и высокая стабильность характеристик;
•высокая точность обработки, которую можно
повысить до любого необходимого значения путем
усложнения аппаратуры;
:
•высокая надежность ввиду ключевых режимов
работы активных элементов;
•автоматизация
проектирования,
удобство
сопряжения с вычислительной техникой.

22.

3. Импульсный метод позволяет просто
решать задачи определения параметров
движущихся
объектов,
получать
импульсную мощность во много раз
превышающую мощность источника
питания.
Импульсные
сигналы
являются
носителями
цифровой
информации, поэтому импульсные
устройства лежат в основе реализации
любых цифровых схем.

23.

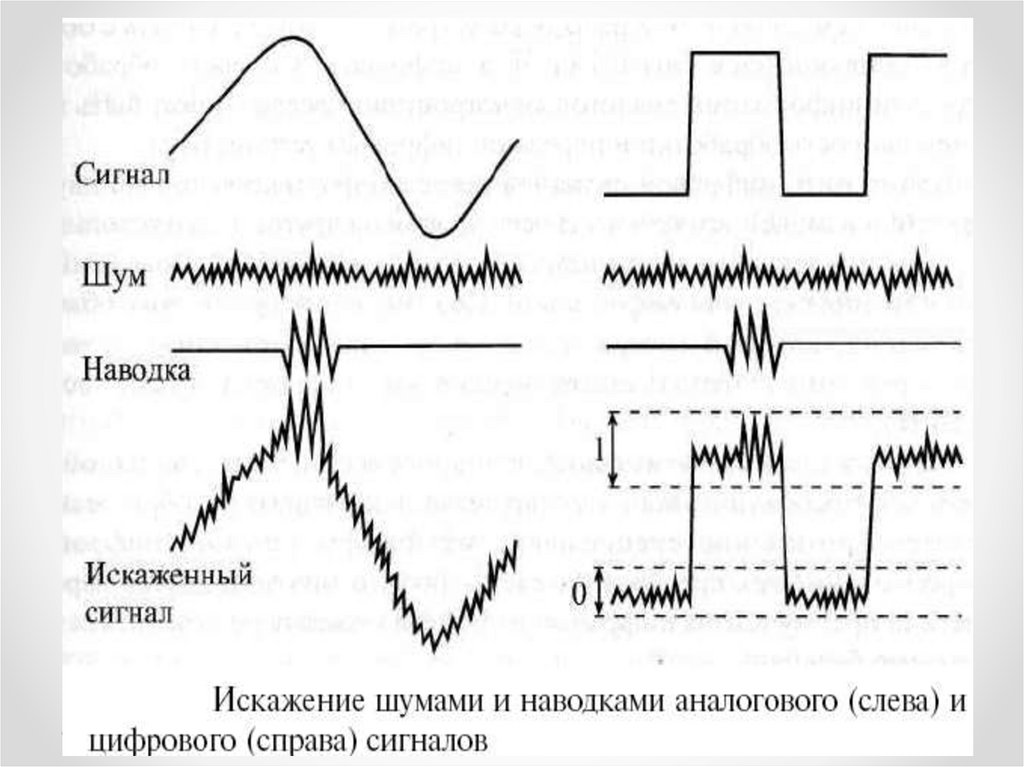
Достоинства цифровых сигналов
Защищены от действия шумов, наводок и
помех гораздо лучше аналоговых.
Более сложная и многоступенчатая обработка, более длительное хранение без
потерь и гораздо более качественную
передачу, чем аналоговые.
Цифровые устройства гораздо меньше
подвержены старению, т.к. небольшое
изменение их параметров никак не
отражается на их функционировании. Их
про-ще проектировать и отлаживать.

24.

25.

Недостатки цифровых сигналов
На каждом из своих разрешенных уровней цифровой сигнал
должен оставаться хотя бы в течении какого-то минимального
интервала времени, иначе его невозможно будет распознать.
Аналоговый сигнал определен в любой момент времени, а цифровой в
дискретном времени (только в выделенные моменты времени),
поэтому максимально достижимое быстродействие аналоговых
устройств всегда принципиально больше, чем цифровых.
Аналоговые устройства могут работать с более быстро меняющимися
сигналами, чем цифровые, поэтому скорость обработки и передачи
информации аналоговым устройством всегда может быть выше,
чем цифровым.
Цифровой сигнал передает информацию только двумя уровнями и
изменением одного своего уровня на другой, а аналоговый еще и
каждым текущим значением своего уровня, т.е. аналоговый сигнал
более емкий, с точки зрения передачи информации.
В природе все сигналы аналоговые, т.е для преобразования их в
цифровые и обратного преобразования требуются АЦП и ЦАП.

26.

ОСНОВЫ АЛГЕБРЫ ЛОГИКИ
Логика – это наука о законах и
формах мышления.
Алгебра логики это начальный
раздел
математической
логики,
которая
занимается
изучением
возможностей
применения
формальных методов для решения
логических задач.

27.

Алгебру логики называют булевой
алгеброй
по
имени
английского
математика Джоржа Буля, который еще в
XIX в. разработал основные положения
исчисления высказываний.
В 40-е гг. XX в. Алгебра логики нашла
широкое применение при составлении и
расчете сложных переключающих схем в
автоматических телефонных станциях. Она
широко применяется при анализе и синтезе
различных цифровых узлов, а также при
машинном решении логических задач.

28.

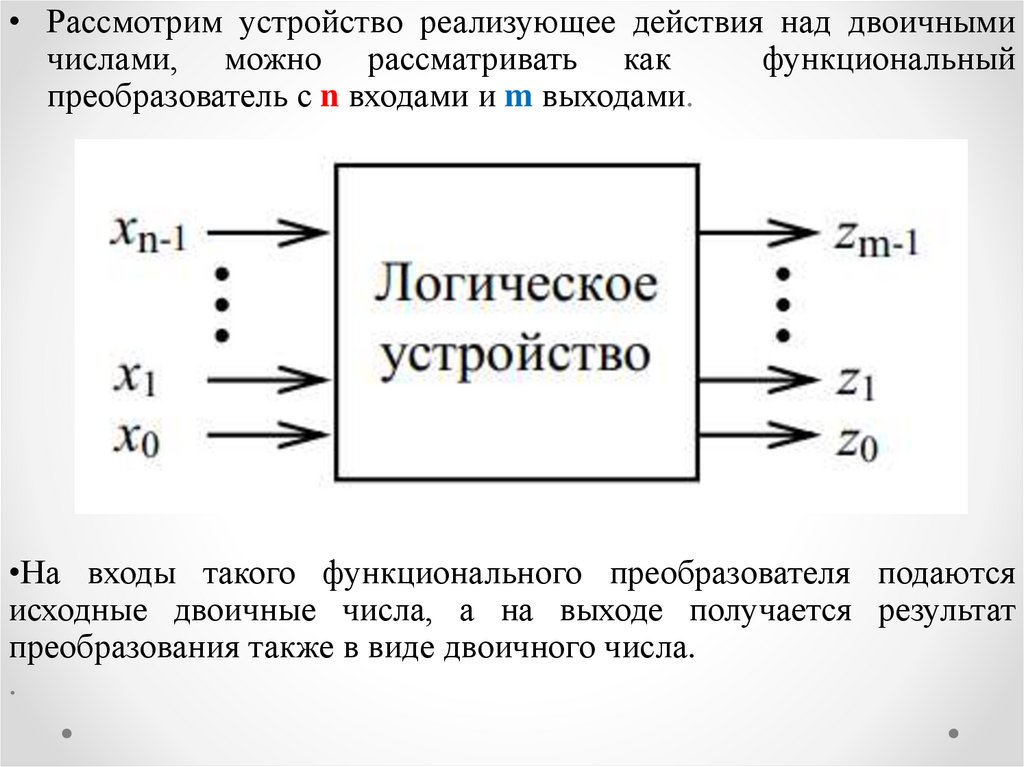
• Рассмотрим устройство реализующее действия над двоичными
числами, можно рассматривать как
функциональный
преобразователь с n входами и m выходами.
•На входы такого функционального преобразователя подаются
исходные двоичные числа, а на выходе получается результат
преобразования также в виде двоичного числа.
.

29.

•Таким образом, значение выходного числа
определяется конкретным сочетанием значений
всех n разрядов входного двоичного числа,
которое называется двоичным набором.
•Каждому набору на входе устройства будет
соответствовать 0 или 1 на соответствующем
выходе.
•Для описания работы такого устройства
используется математический аппарат алгебры
логики или булевой алгебры.

30.

• Начальным понятием алгебры логики
является понятие высказывания.
• Высказывание - это любое утверждение,
которое может быть истинным или
ложным.
• Над высказыванием можно выполнять
некоторые математические операции, так
как
каждое
высказывание
можно
рассматривать как двоичную переменную.

31.

• Примером двоичной переменной может
служить значение какого-либо разряда
двоичного числа, которое может быть
нулем либо единицей.
• В соответствии с двоичной природой
высказываний, их условились называть
логическими переменными и обозначать
буквами латинского алфавита, приписывая
им значение 1 в случае истинности и
значение 0 в случае ложности, например
и т.д.

32.

• Высказывания
сложными.
могут
быть
простыми
и
• Простое высказывание содержит одну
простую законченную мысль. Значение
истинности простого высказывания не
зависит от значений истинности каких либо
других высказываний.
• Сложным
называется
высказывание,
значение истинности которого зависит от
значений других высказываний.

33.

• Любое сложное высказывание можно считать
логической (булевой) функцией некоторых
двоичных аргументов – простых высказываний,
входящих в его состав.
• Сложные высказывания, в свою очередь, также
могут служить аргументами еще более сложных
логических функций, т.е. при построении
логических функций справедлив принцип
суперпозиции.
• Следовательно,
что
можно
построить
логическую функцию любой сложности,
пользуясь ограниченным числом логических
связок (операций) и принципом суперпозиции.

34.

Функцией алгебры
логики является функция,
однозначно определяющая
соответствие каждого
двоичного набора 0 или 1.

35.

• Логическая операция это простейшее действие
над
логическими
аргументами,
например
логическое отрицание, логическое умножение и
т.п.
• Элементарной называется логическая функция,
которая содержит только одну логическую
операцию.
• Логическим
элементом
называется
электрическая схема, реализующая элементарную
логическую функцию.
• Логическими или цифровыми называются
устройства, реализующие логические функции
любой сложности.

36.

В цифровой технике для обозначения
различной информации пользуются
кодовыми словами, которые
представляют собой
последовательность символов 0 и 1
(логических переменных), например
10111011.

37.

Классификация цифровых
устройств
• 1 По способу ввода и вывода кодовых слов
различают
логические
устройства
параллельного,
последовательного
и
смешанного действия.
• 2 По способу функционирования логические
(цифровые) устройства (и их узлы) делятся на
два класса: комбинационные цифровые
устройства (КЦУ) и последовательностные
цифровые устройства (ПЦУ).

38.

• В КЦУ (цифровых автоматах без памяти) каждый
символ на выходе определяется комбинацией
символов на входах в текущий момент времени и
не зависит от того, какие символы ранее
действовали на этих входах, т.е. КЦУ не обладают
памятью.
• В ПЦУ (цифровых автоматах с памятью)
выходной сигнал определяется не только набором
символов на входах в текущий момент времени, но
и внутренним состоянием устройства, которое
зависит от предыдущих значений символов на
входах, т.е. ПЦУ обладают памятью.

39.

• Аналитический
логическая
функция
записывается
в
форме
логического
выражения,
показывающего, какие и в какой
последовательности
должны
выполнятся
логические
операции над аргументами
функции, например
• Табличный
строится таблица истинности, в
которой
приводятся
все
возможные
значения
наборов
аргументов и значения логической
функции, которые она принимает
на каждом наборе. Число наборов
аргументов N, т.е. число строк в
таблице истинности, определяется
по формуле N=2ª где a – число
аргументов.
аргументы
f (X1 ,X2 ,X3 ) X 1 X2 X 3 .
функци
я
х1
х2
F(х1,х2)
0
0
1
0
1
0
1
0
0
1
1
1

40.

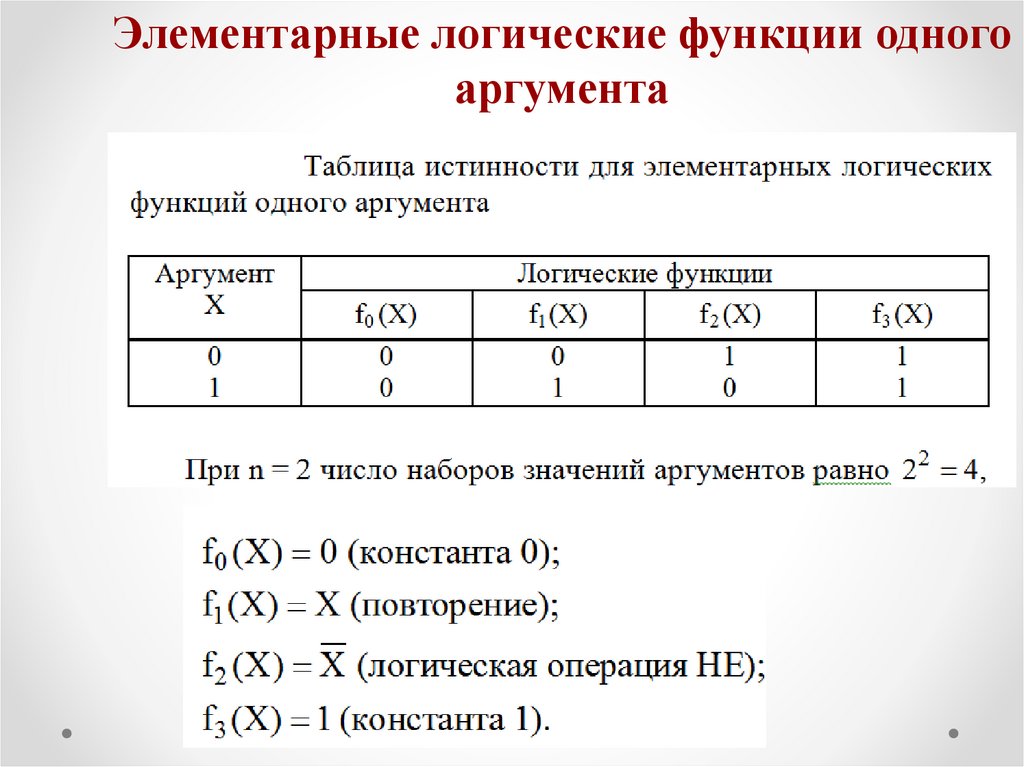
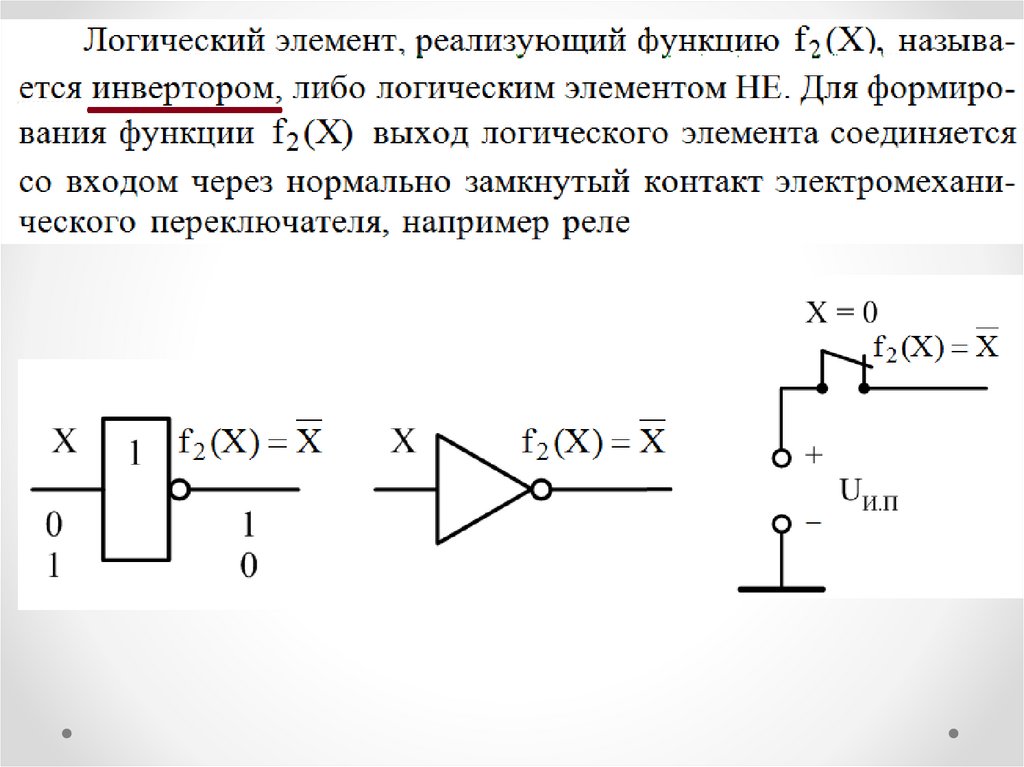
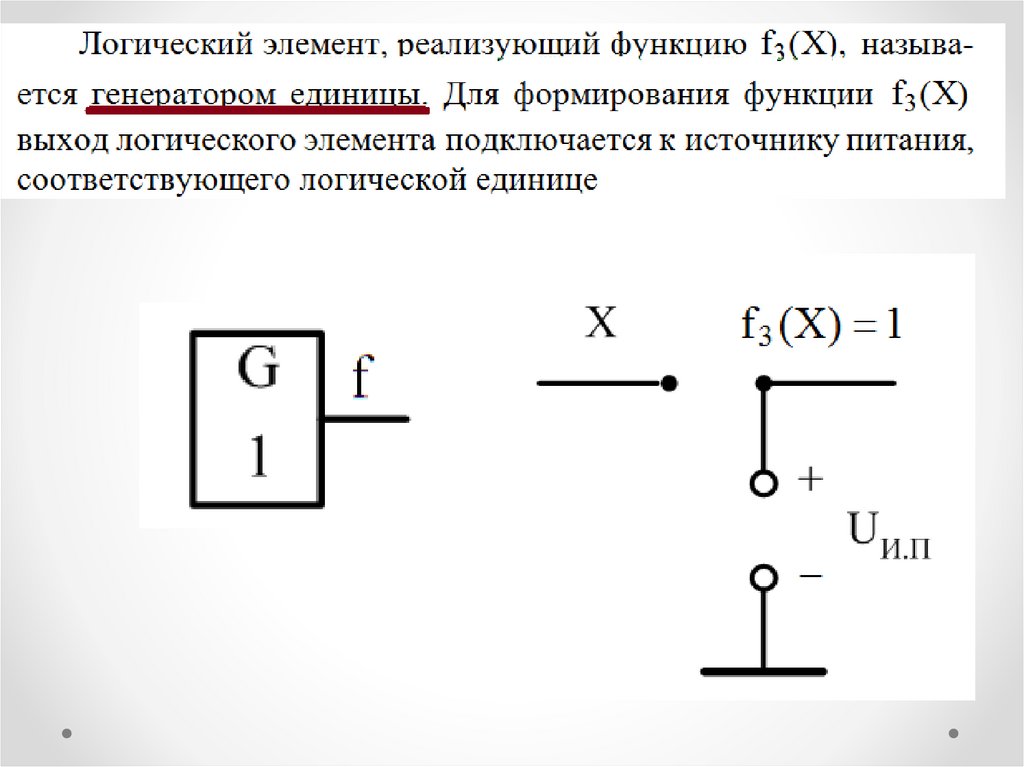
Элементарные логические функции одного
аргумента

41.

42.

43.

44.

45.

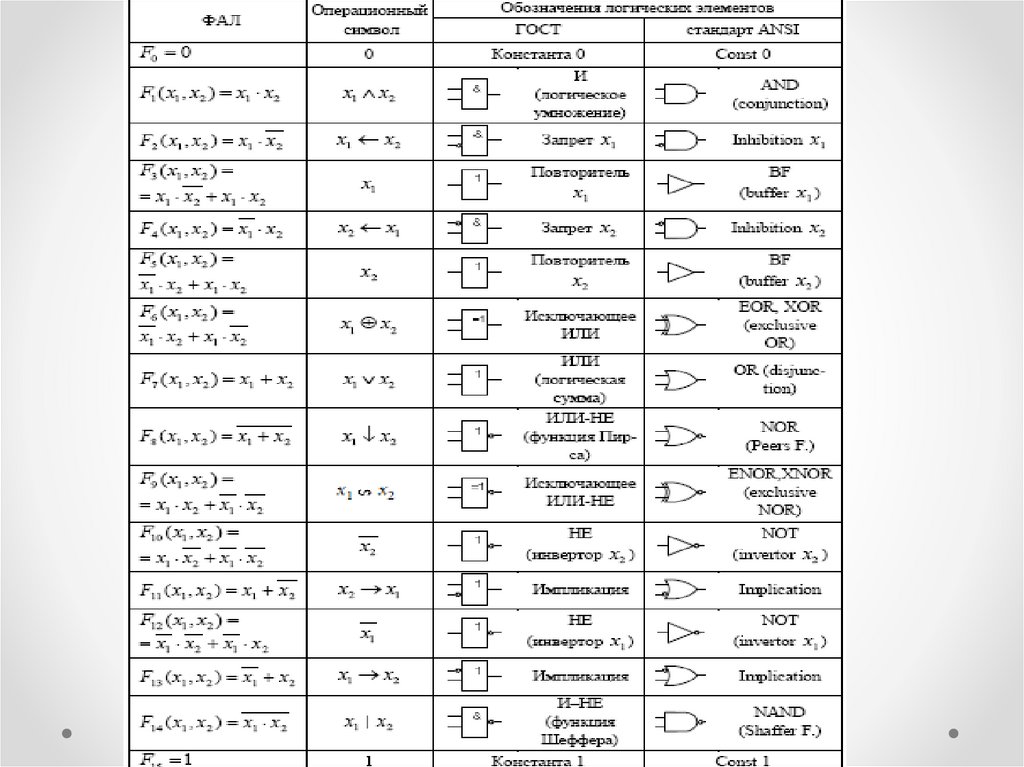
Элементарные логические функции двух
аргументов
Логические функции могут быть многоаргументными.
На основе законов алгебры логики все они могут быть
выражены через функции с числом аргументов не более
двух. Все логические функции с числом аргументов не
более двух являются элементарными, так как содержат
только одну логическую операцию.

46.

Таблица истинности для
элементарных логических
функций двух аргументов

47.

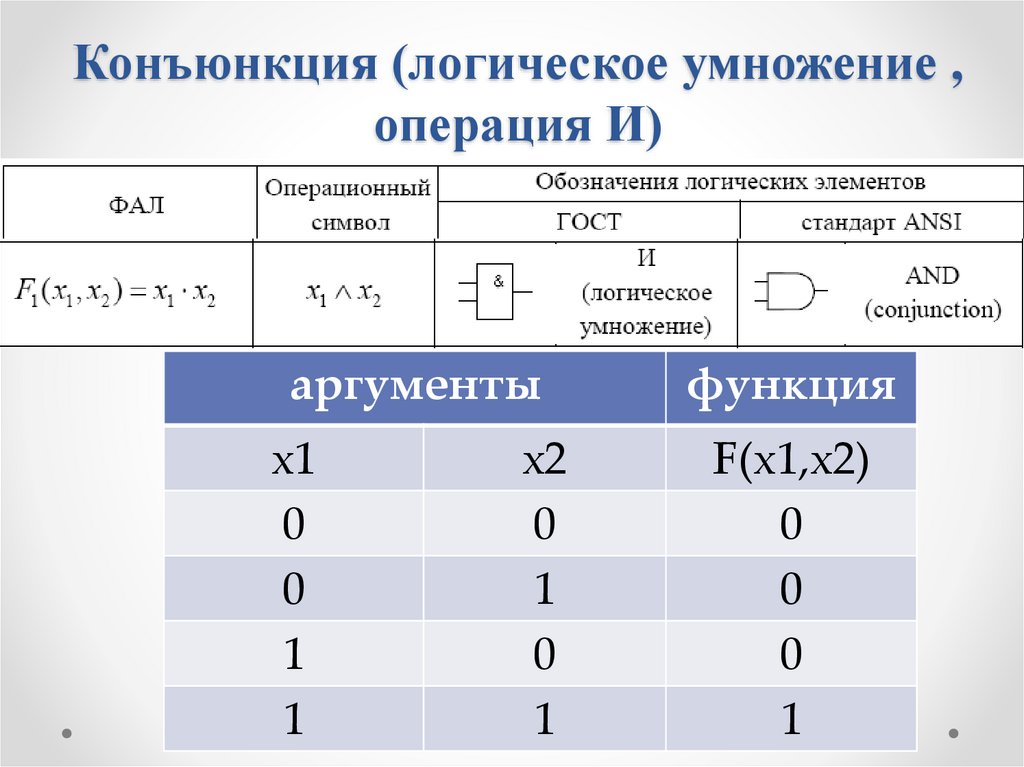
48.

Конъюнкция (логическое умножение ,
операция И)
аргументы
функция
х1
0
0
1
1
F(х1,х2)
0
0
0
1
х2
0
1
0
1

49.

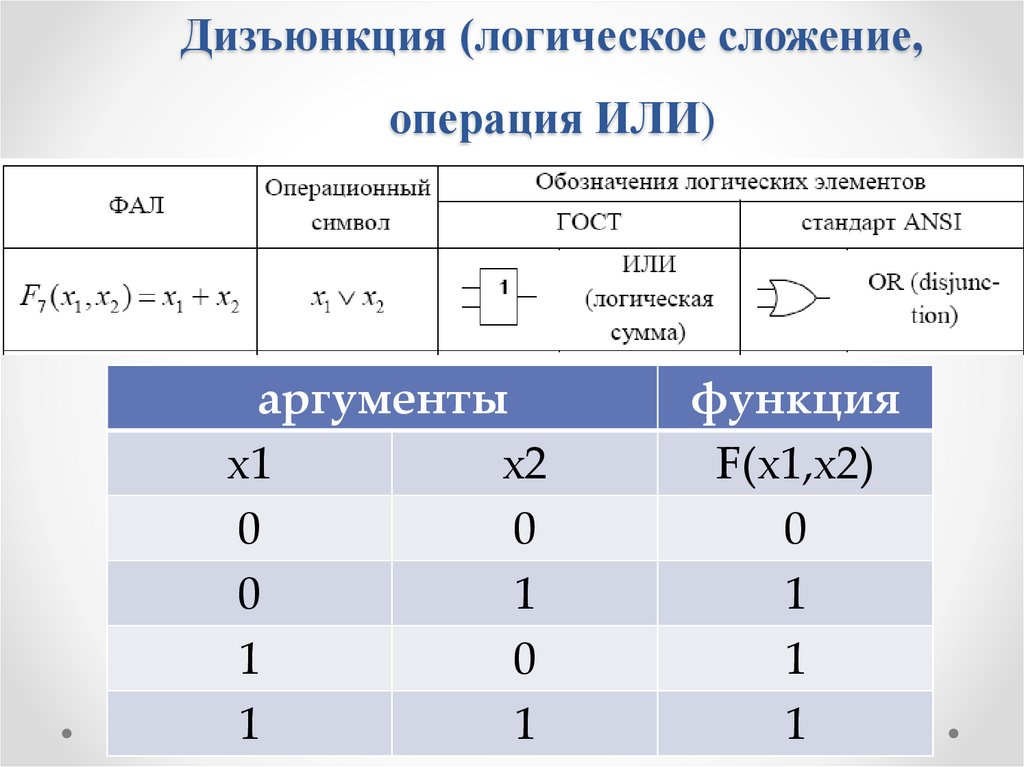
Дизъюнкция (логическое сложение,
операция ИЛИ)
аргументы
х1
х2
0
0
0
1
1
0
1
1
функция
F(х1,х2)
0
1
1
1

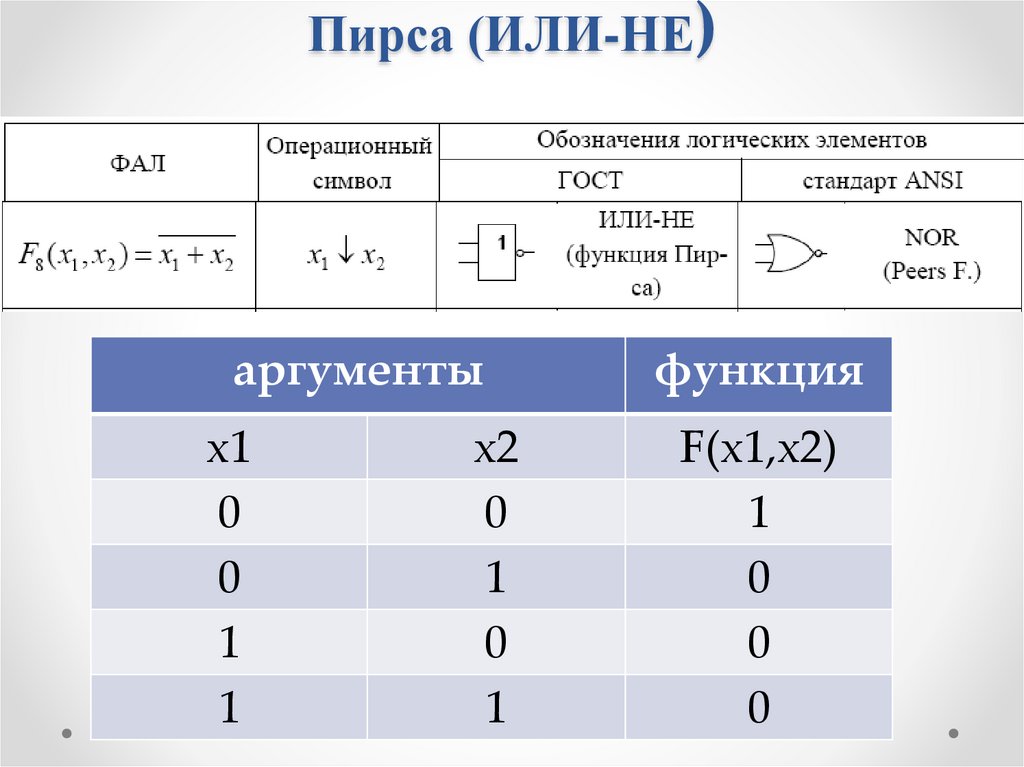
50.

Пирса (ИЛИ-НЕ)
аргументы
функция
х1
0
0
1
1
F(х1,х2)
1
0
0
0
х2
0
1
0
1

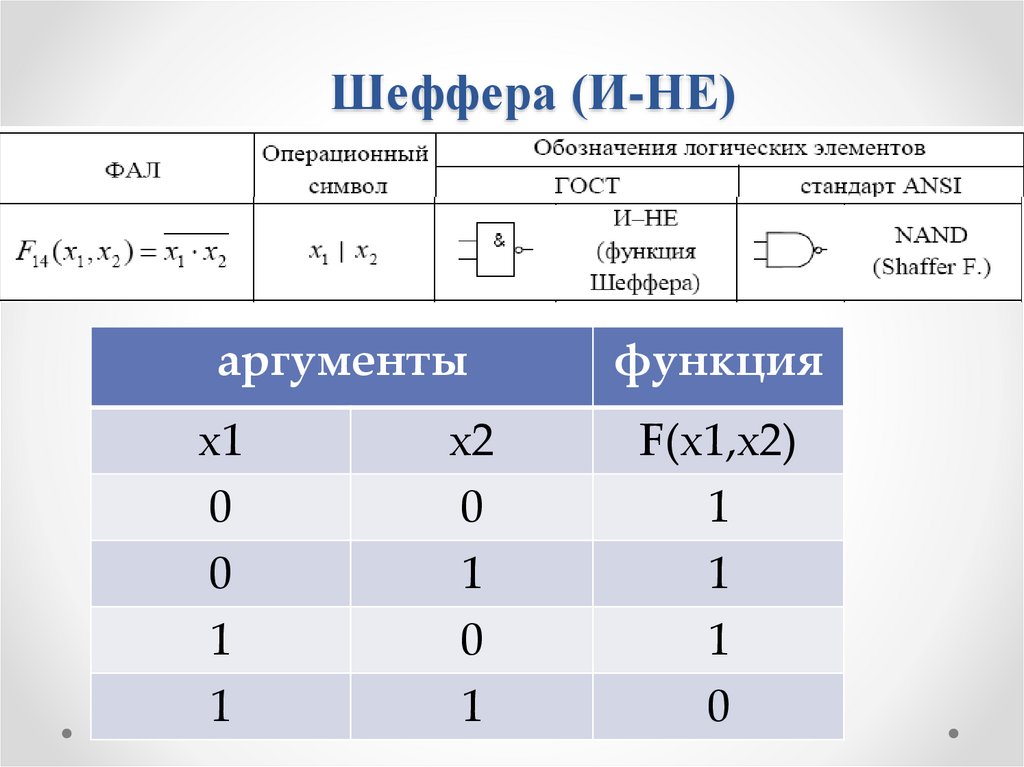
51.

Шеффера (И-НЕ)
аргументы
функция
х1
0
0
1
1
F(х1,х2)
1
1
1
0
х2
0
1
0
1

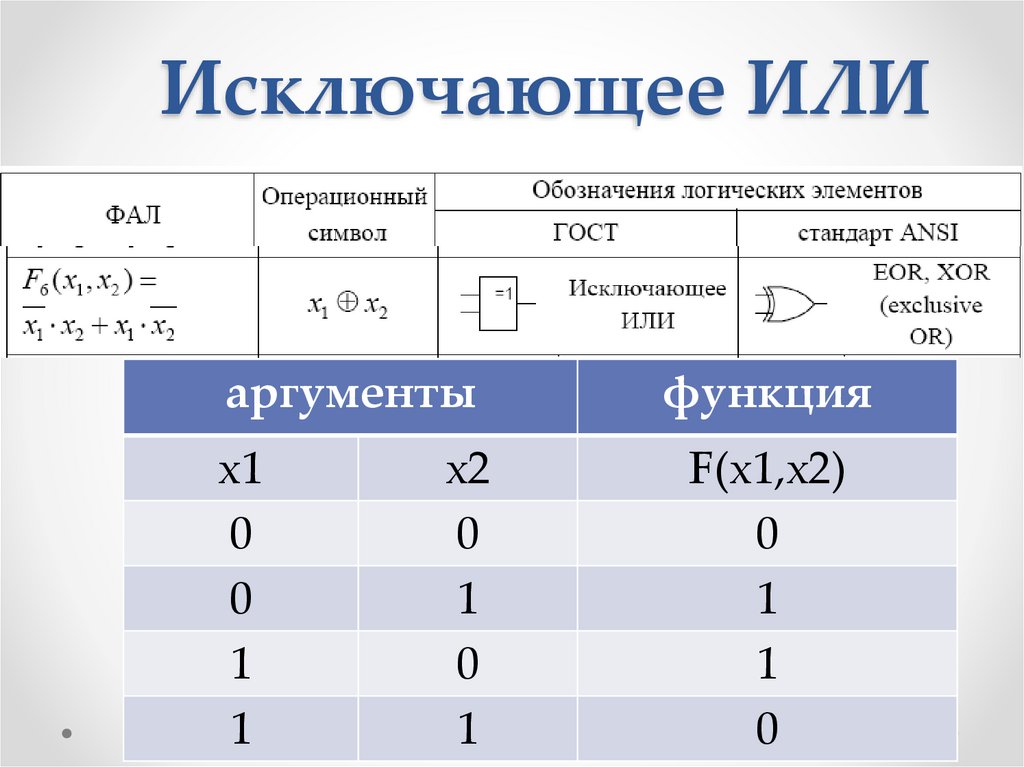
52.

Исключающее ИЛИ
аргументы
функция
х1
0
0
1
1
F(х1,х2)
0
1
1
0
х2
0
1
0
1

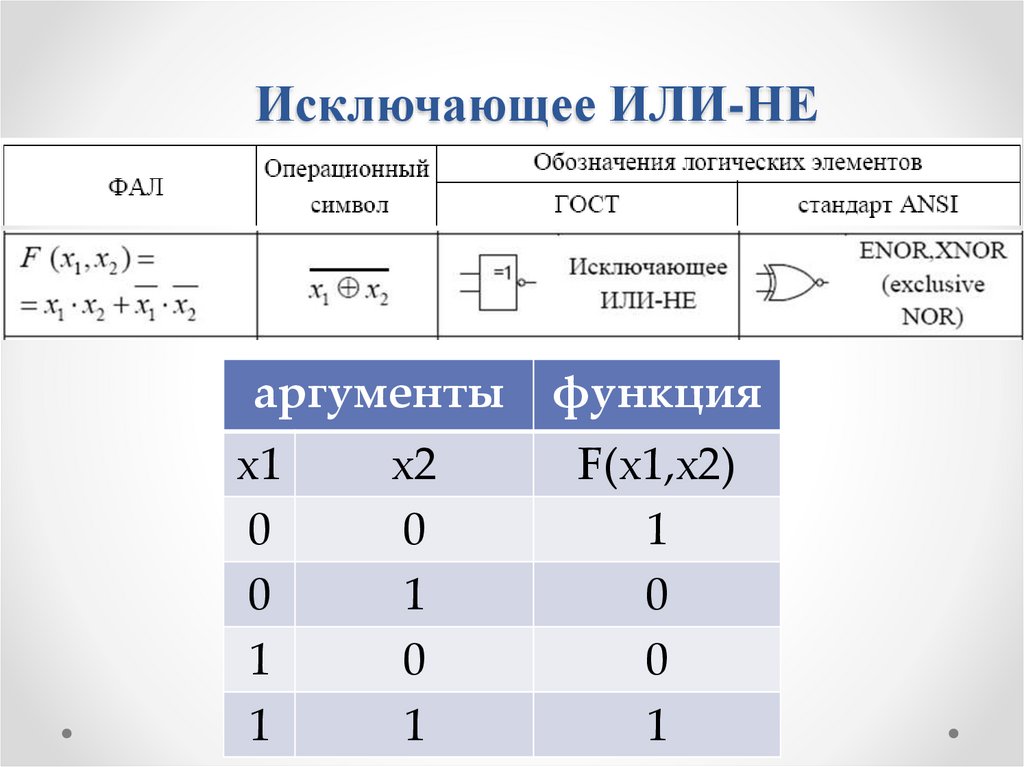
53.

Исключающее ИЛИ-НЕ
аргументы
функция
х1
0
0
1
1
F(х1,х2)
1
0
0
1
х2
0
1
0
1