Пересечение двух сфер

1. Пересечение двух сфер

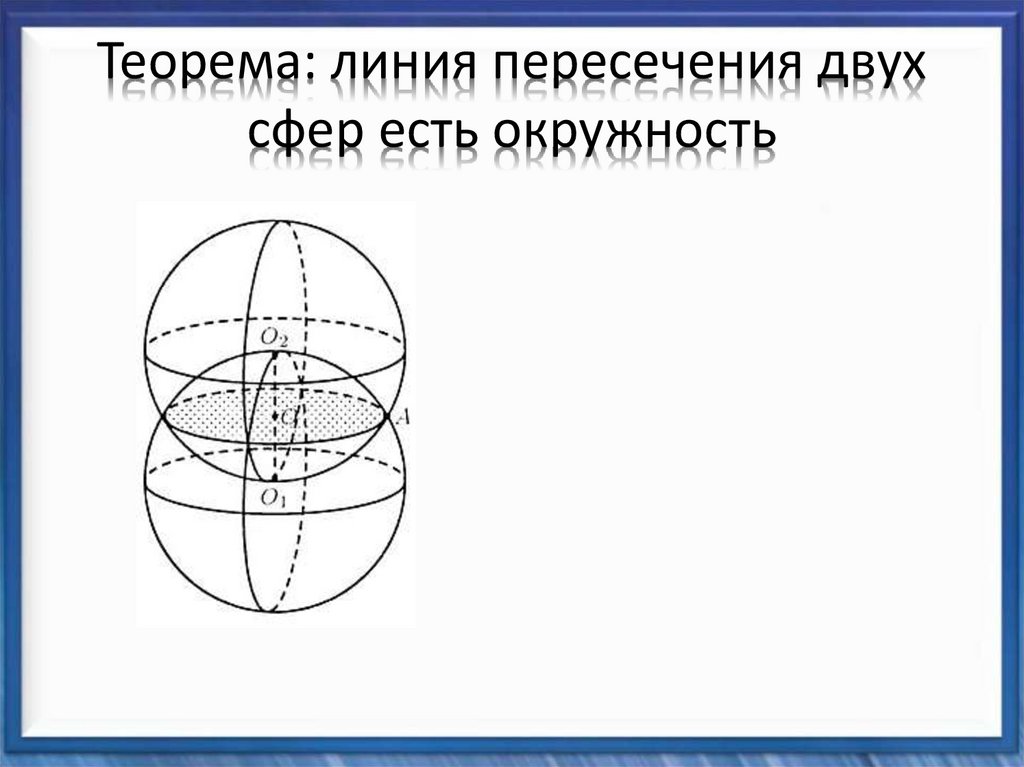
2. Теорема: линия пересечения двух сфер есть окружность

3. Теорема: линия пересечения двух сфер есть окружность

4. Теорема: линия пересечения двух сфер есть окружность

Дано: сфера (О1, R), сфера (О2, R),
А – точка пересечения
Доказать: линия пересечения –
окружность
Доказательство:

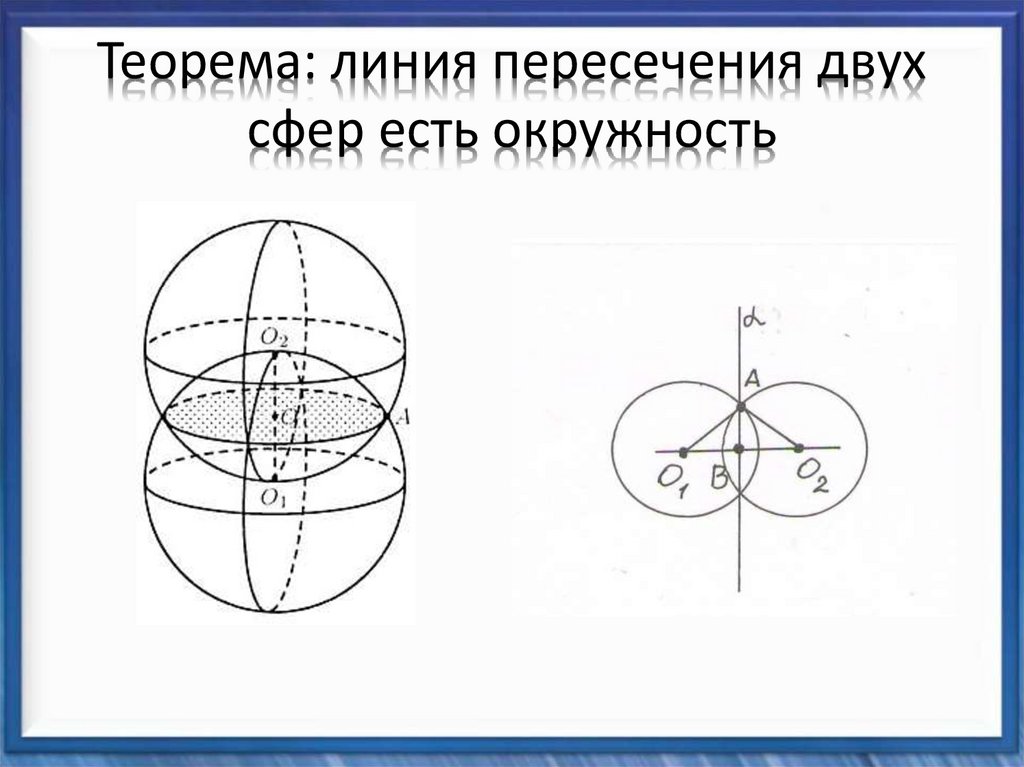
5. Теорема: линия пересечения двух сфер есть окружность

Доказательство:
1. через А проведем α
перпендикулярную О1О2
2. α∩сферы по окружности
(В,АВ),
3. т.о. окружность (В,АВ)линия пересечения сфер.

6. Задача1. два равных шара радиуса R расположены так, что центр одного лежит на поверхности другого. Найти длину линии, по

которой пересекаются их поверхности
• Дано: сфера (О, R) пересекает
сферу (О1 , R)
• Найти: длину линии
пересечения.

7. Задача 2. Две сферы, радиусы которых 15 и 20, пересекаются по окружности, радиус которой равен 12. Найти расстояние между

центрами сфер, если они находятся по разные стороны от линии
пересечения.
• Дано: сфера (О1,R1 ), сфера
(О2, R2), R1 = 20, R2 = 15
• Найти: О1 О2
О

8. Задача 3. Две сферы, радиусы которых 15 и 20, пересекаются по окружности, радиус которой равен 12. Найти расстояние между

центрами сфер, если они находятся по одну сторону от линии
пересечения.
• Дано: сфера (О1,R1 ), сфера
(О2, R2), R1 = 20, R2 = 15
• Найти: О1 О2
О

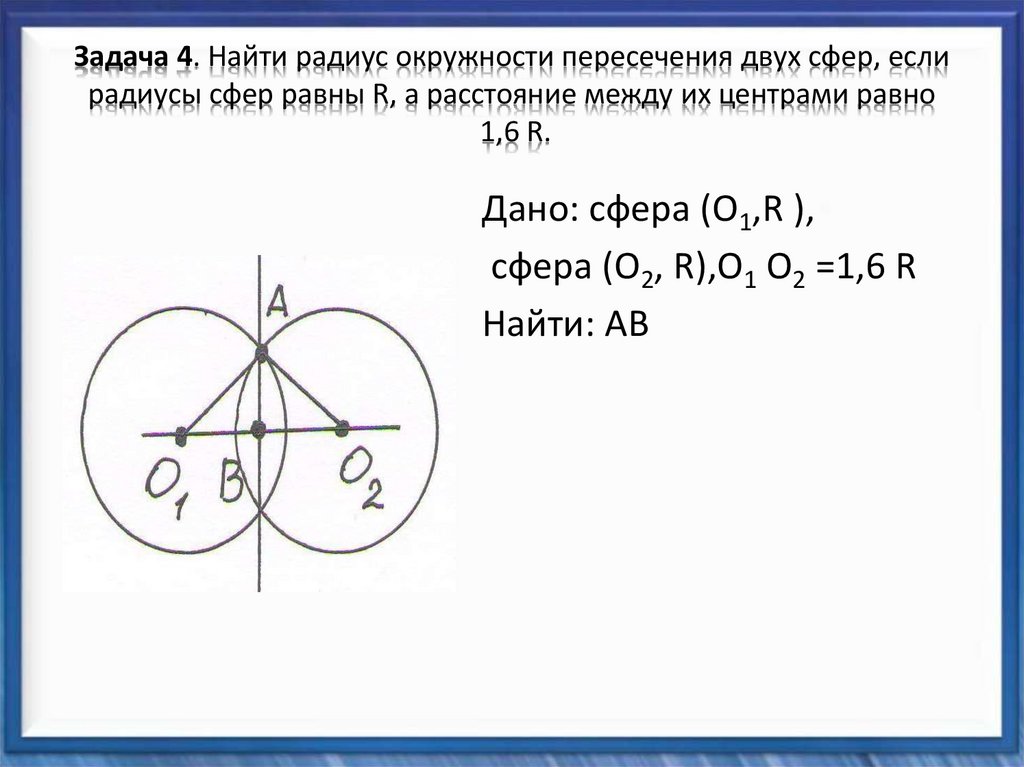
9. Задача 4. Найти радиус окружности пересечения двух сфер, если радиусы сфер равны R, а расстояние между их центрами равно 1,6 R.

Дано: сфера (О1,R ),
сфера (О2, R),О1 О2 =1,6 R
Найти: АВ

10. Домашнее задание:

• п.62 в.20 устно
• № 45

11. На этом наш урок закончен