Похожие презентации:
Пересечение двух плоскостей. Пересечение прямой с плоскостью
1. Пересечение двух плоскостей Пересечение прямой с плоскостью Автор:Леонова О.Н.
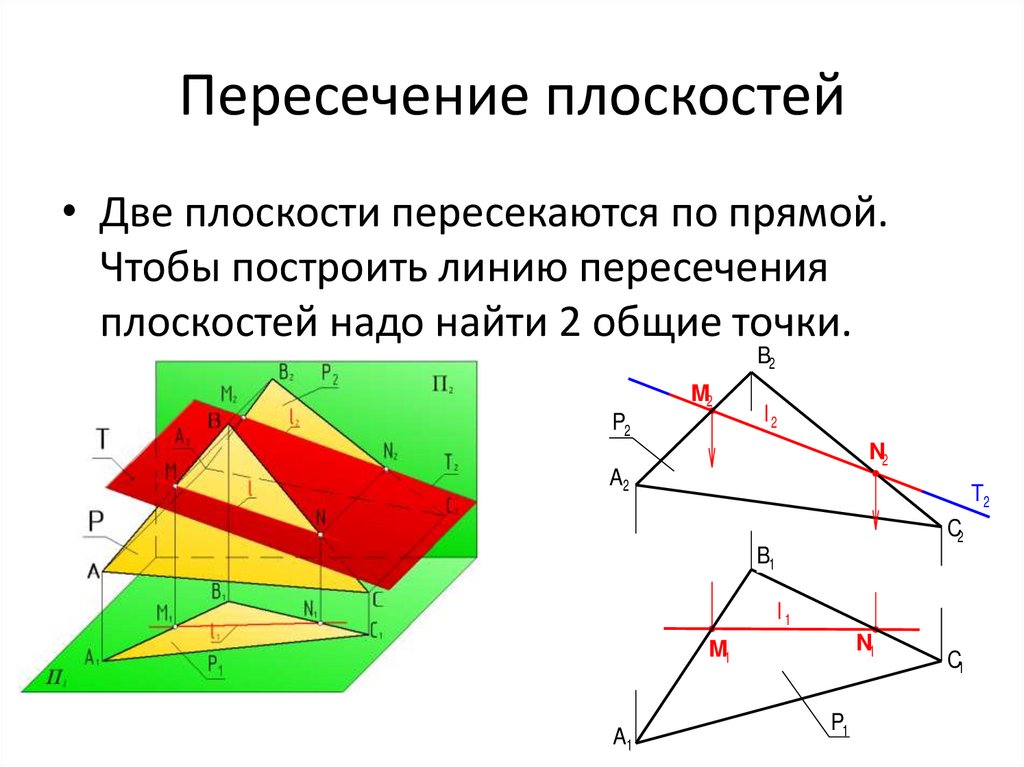
2. Пересечение плоскостей
• Две плоскости пересекаются по прямой.Чтобы построить линию пересечения
плоскостей надо найти 2 общие точки.
B2
M2
P2
l2
N2
A2
T2
C2
B1
l1
N1
M1
A1
P1
C1
3.
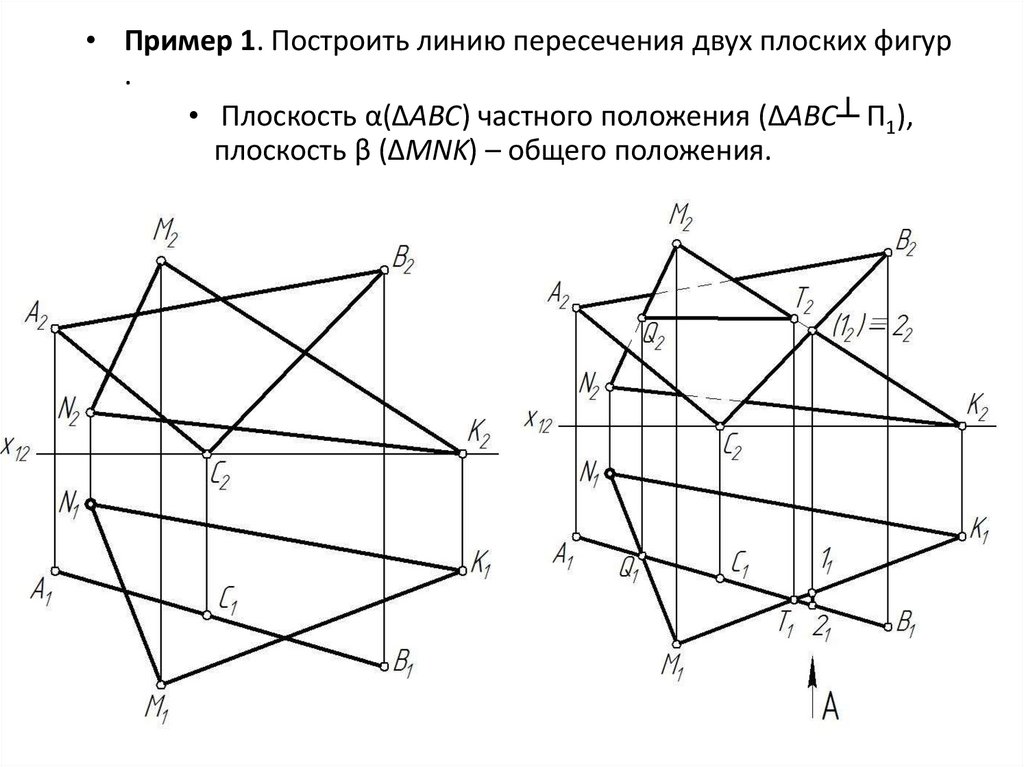
• Пример 1. Построить линию пересечения двух плоских фигур.
• Плоскость α(ΔАВС) частного положения (ΔАВС┴ П1),
плоскость β (ΔMNK) – общего положения.
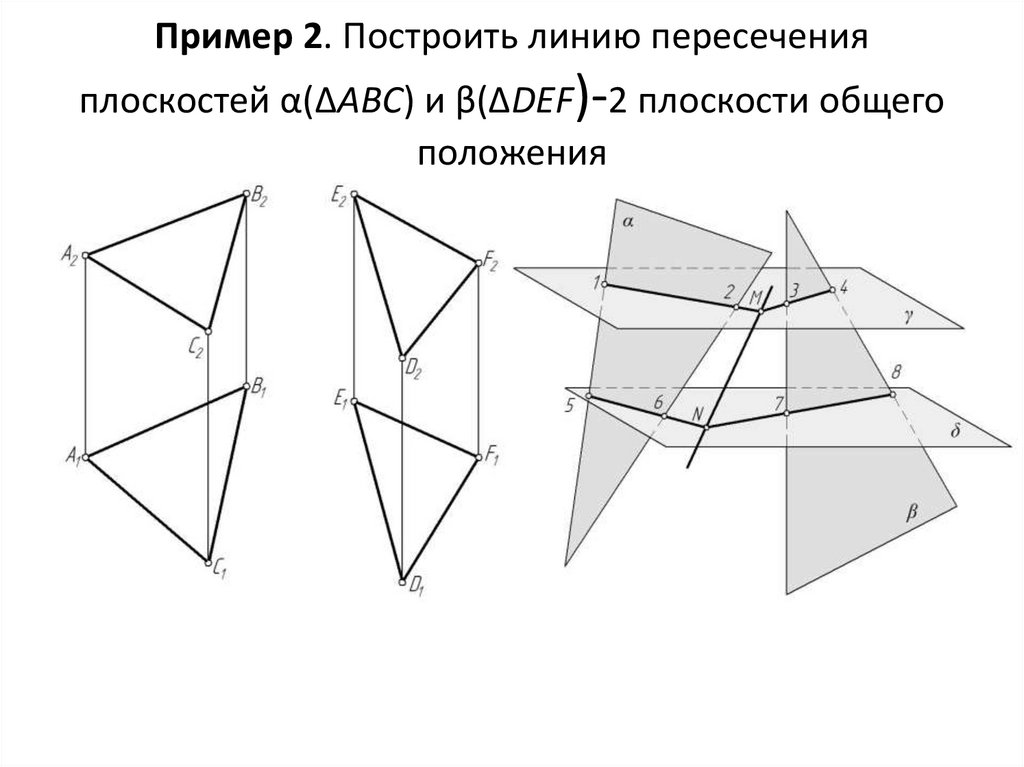
4. Пример 2. Построить линию пересечения плоскостей α(ΔАВС) и β(ΔDEF)-2 плоскости общего положения
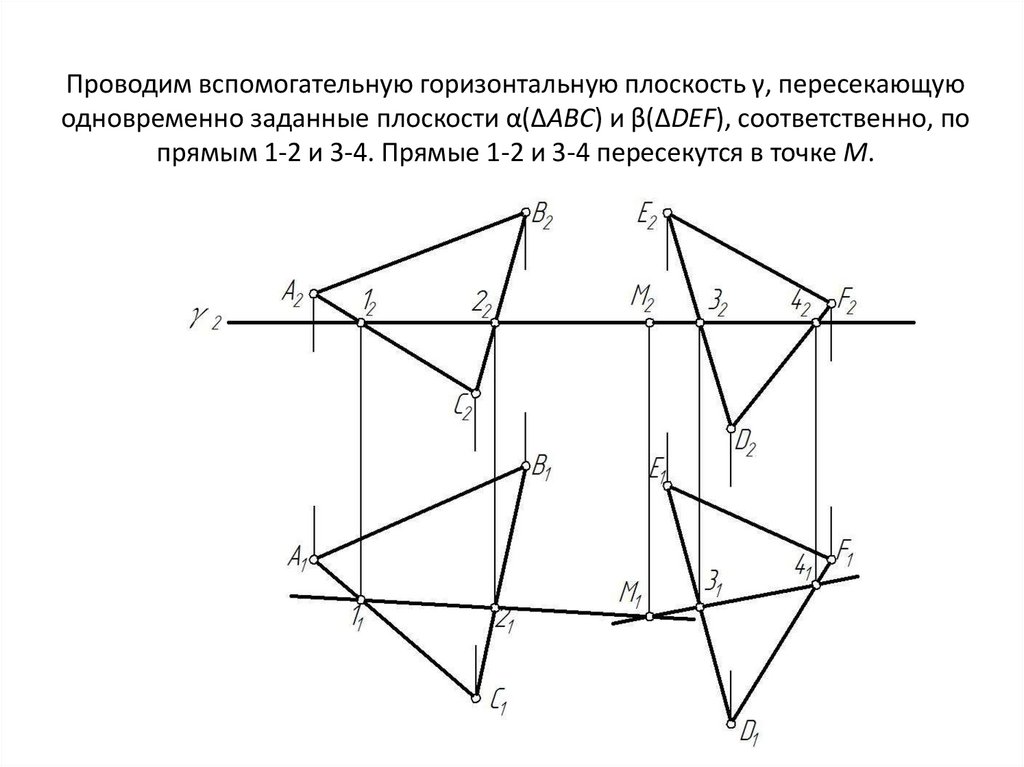
5. Проводим вспомогательную горизонтальную плоскость γ, пересекающую одновременно заданные плоскости α(ΔАВС) и β(ΔDEF),
соответственно, попрямым 1-2 и 3-4. Прямые 1-2 и 3-4 пересекутся в точке М.
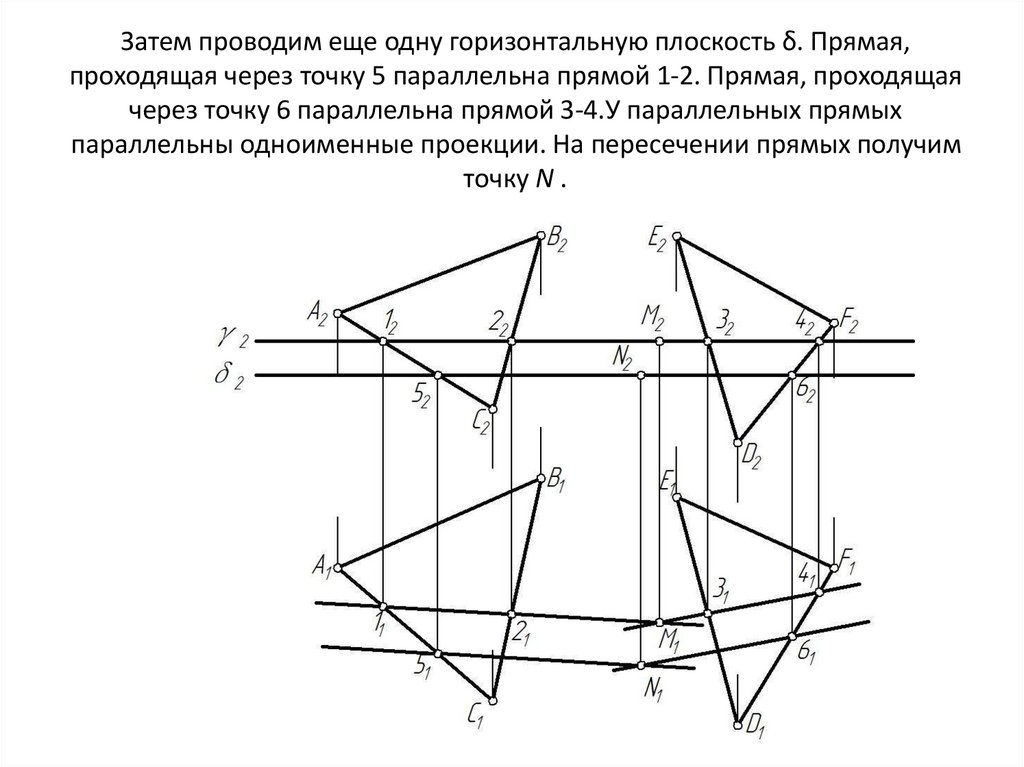
6. Затем проводим еще одну горизонтальную плоскость δ. Прямая, проходящая через точку 5 параллельна прямой 1-2. Прямая, проходящая
через точку 6 параллельна прямой 3-4.У параллельных прямыхпараллельны одноименные проекции. На пересечении прямых получим
точку N .
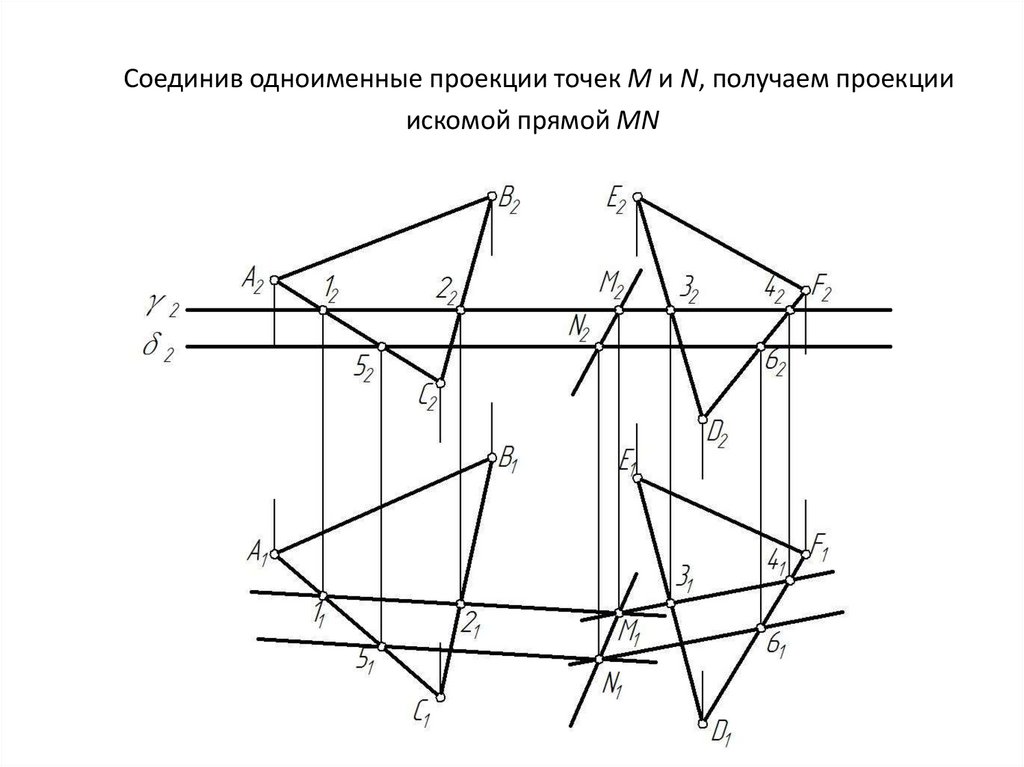
7. Соединив одноименные проекции точек М и N, получаем проекции искомой прямой МN
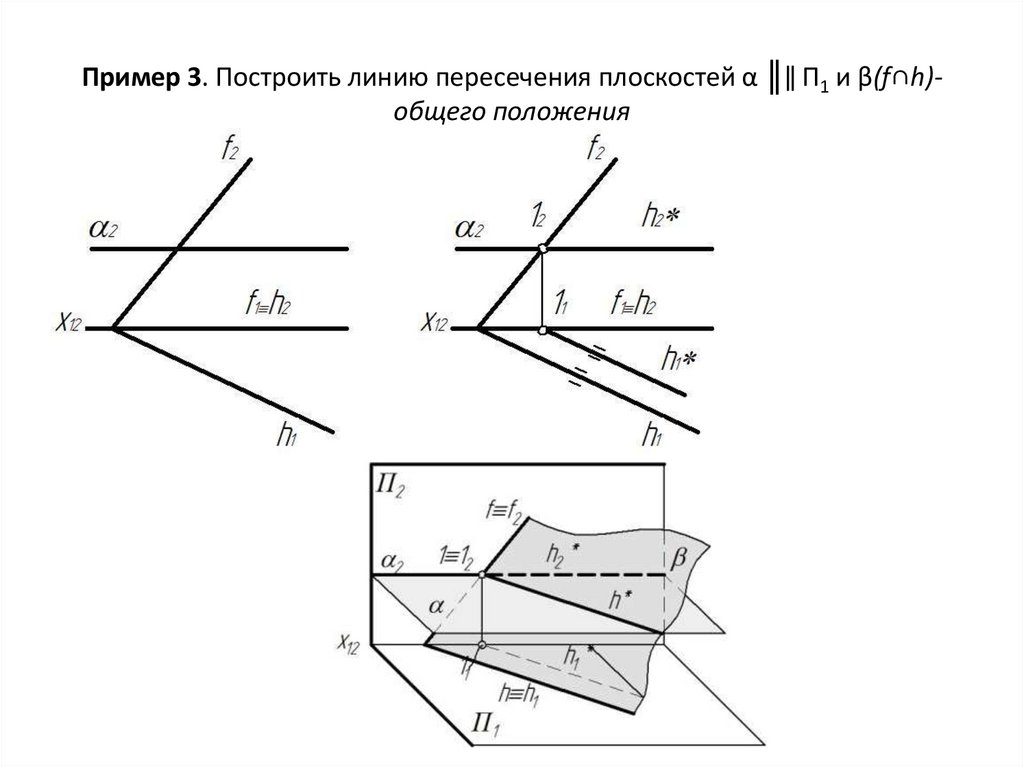
8. Пример 3. Построить линию пересечения плоскостей α ║‖ П1 и β(f∩h)-общего положения
Пример 3. Построить линию пересечения плоскостей α ║‖ П1 и β(f∩h)общего положения9. Пересечение прямой линии с плоскостью
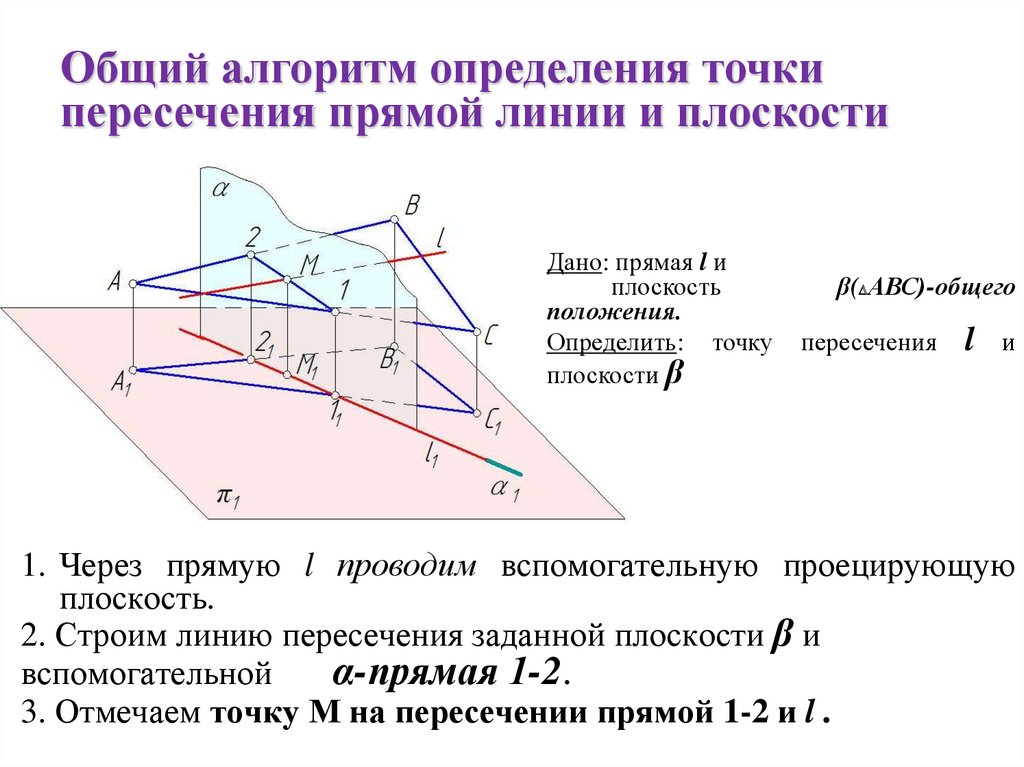
10. Общий алгоритм определения точки пересечения прямой линии и плоскости
Дано: прямая l иплоскость
положения.
Определить: точку
плоскости β
β( АВС)-общего
пересечения
l
и
1. Через прямую l проводим вспомогательную проецирующую
плоскость.
2. Строим линию пересечения заданной плоскости β и
вспомогательной
α-прямая 1-2.
3. Отмечаем точку М на пересечении прямой 1-2 и l .
11.
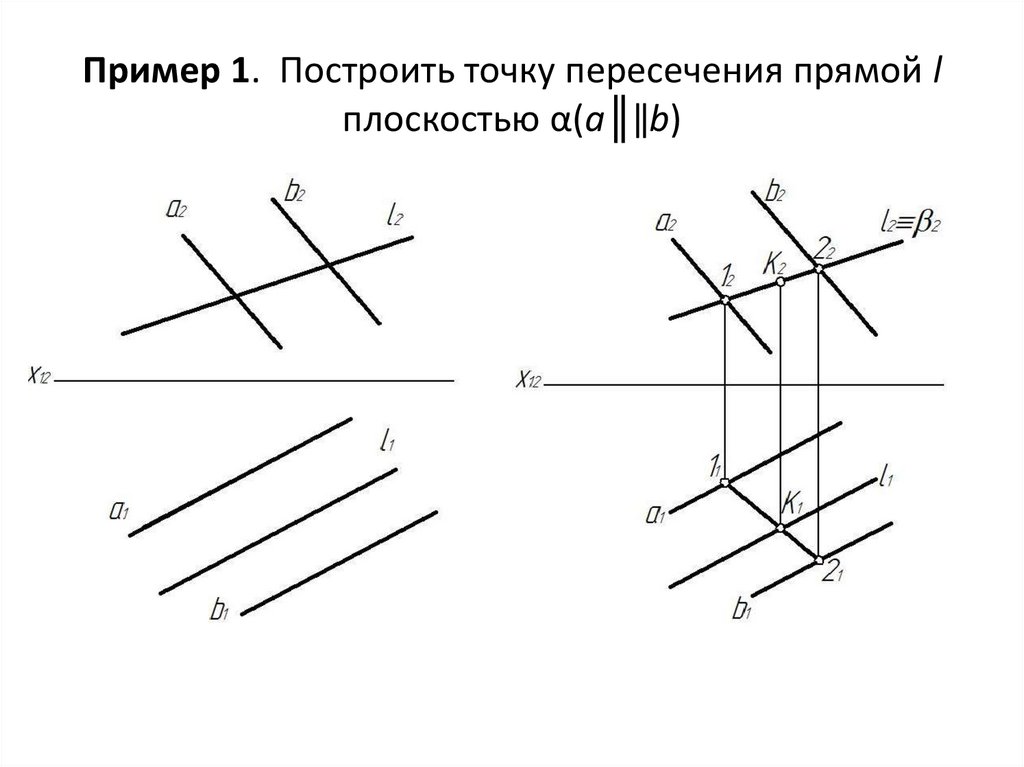
12. Пример 1. Построить точку пересечения прямой l плоскостью α(а║‖b)
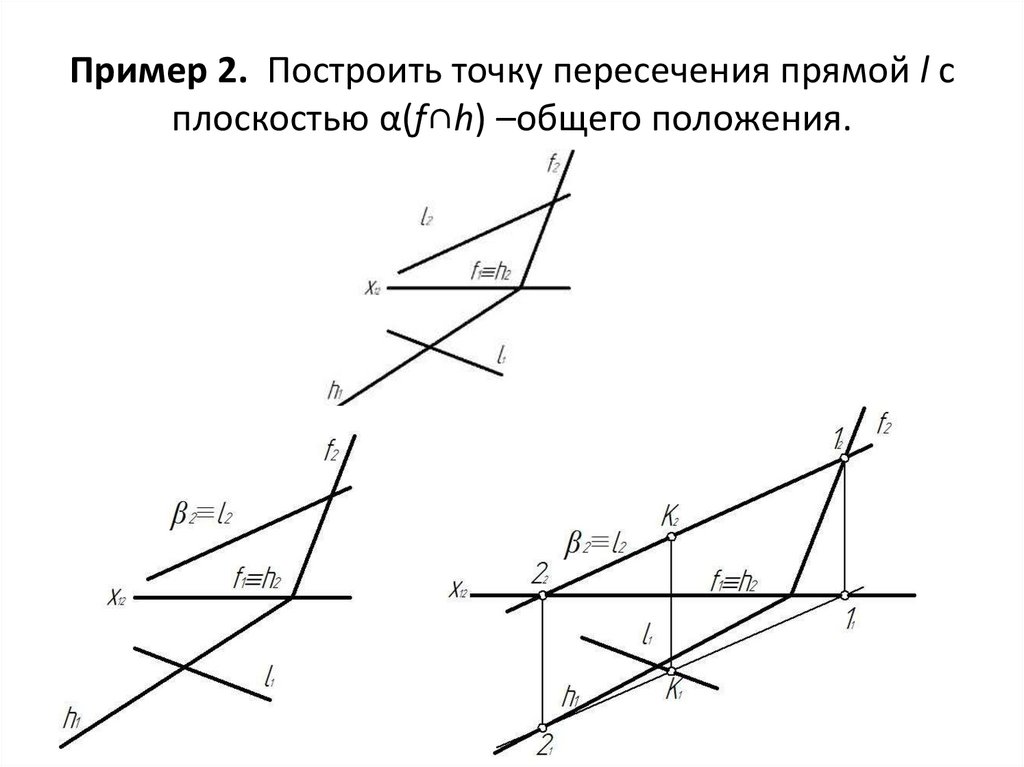
13. Пример 2. Построить точку пересечения прямой l с плоскостью α(f∩h) –общего положения.
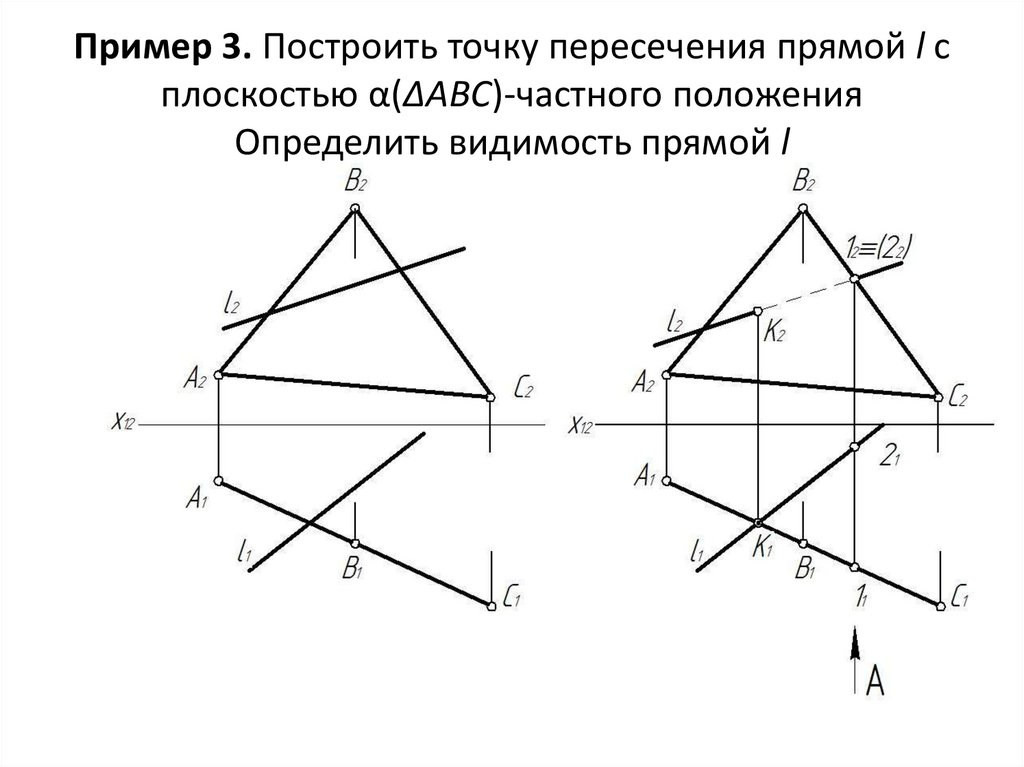
14. Пример 3. Построить точку пересечения прямой l с плоскостью α(ΔАВС)-частного положения Определить видимость прямой l
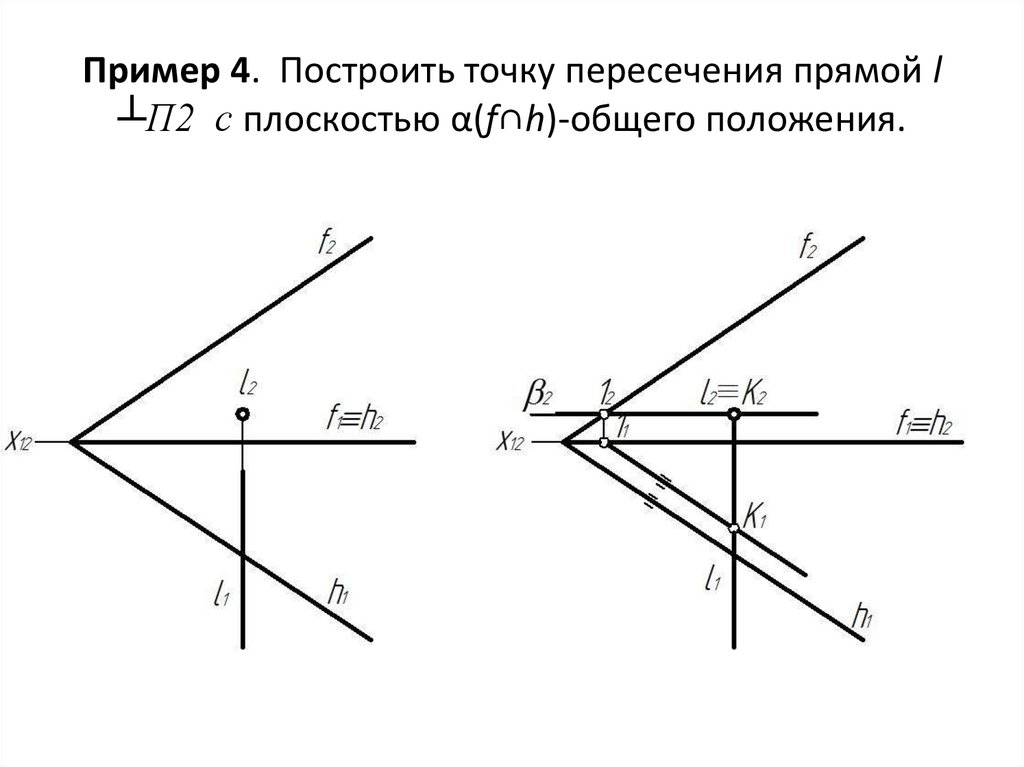
15. Пример 4. Построить точку пересечения прямой l ┴П2 с плоскостью α(f∩h)-общего положения.
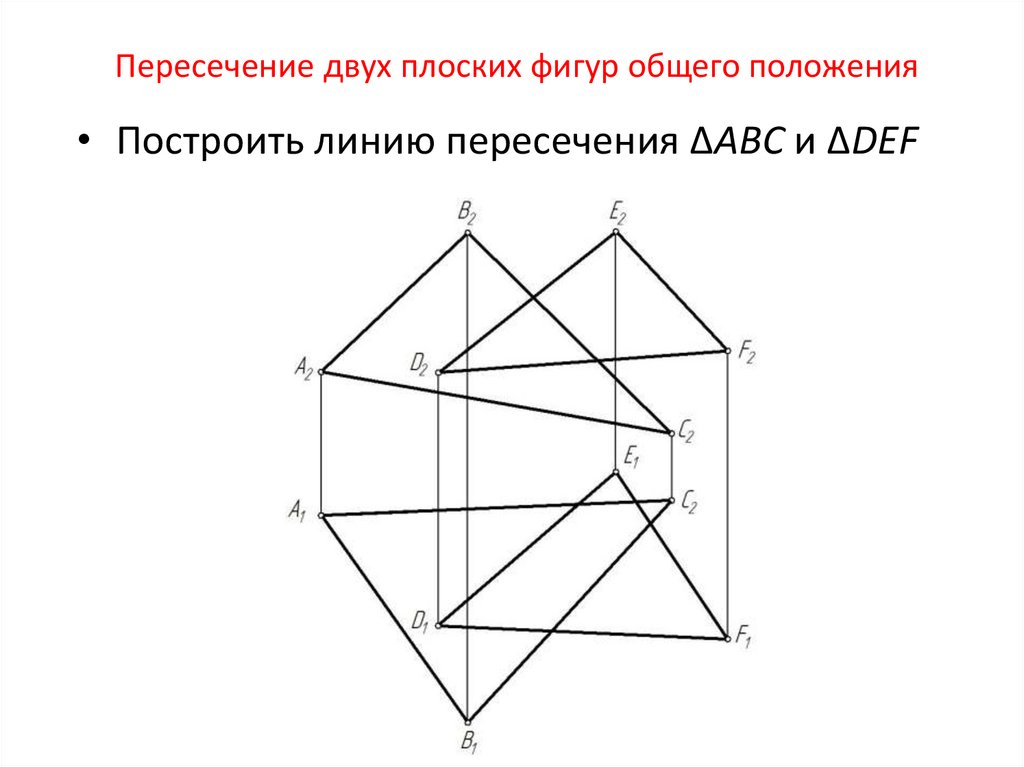
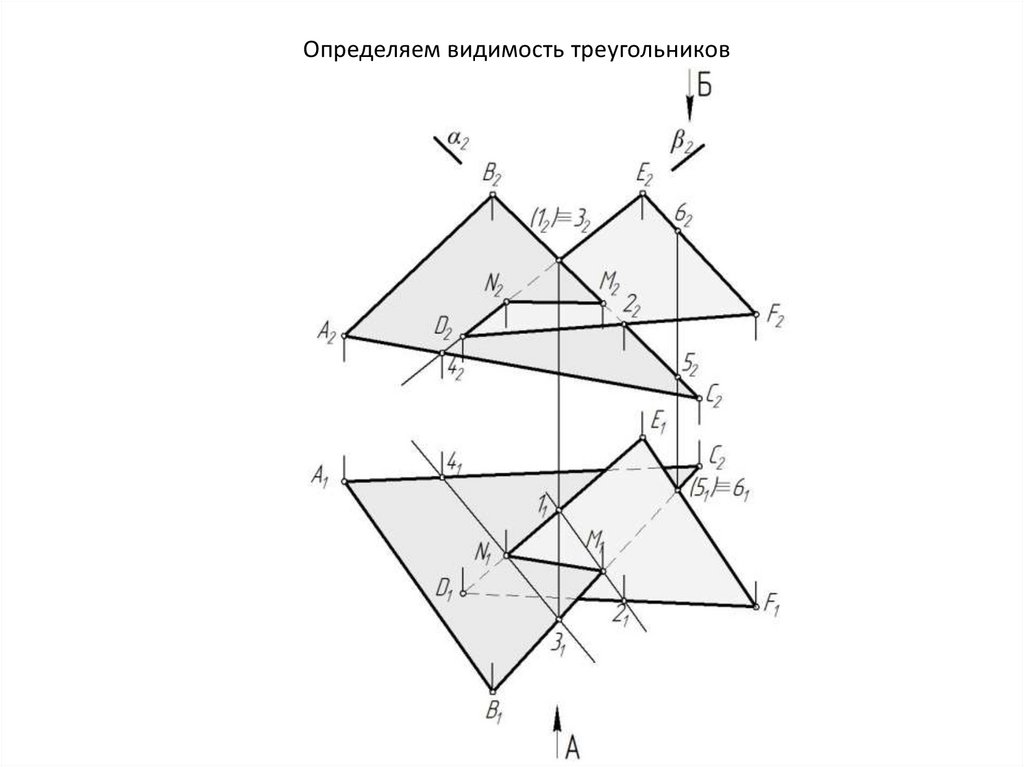
16. Пересечение двух плоских фигур общего положения
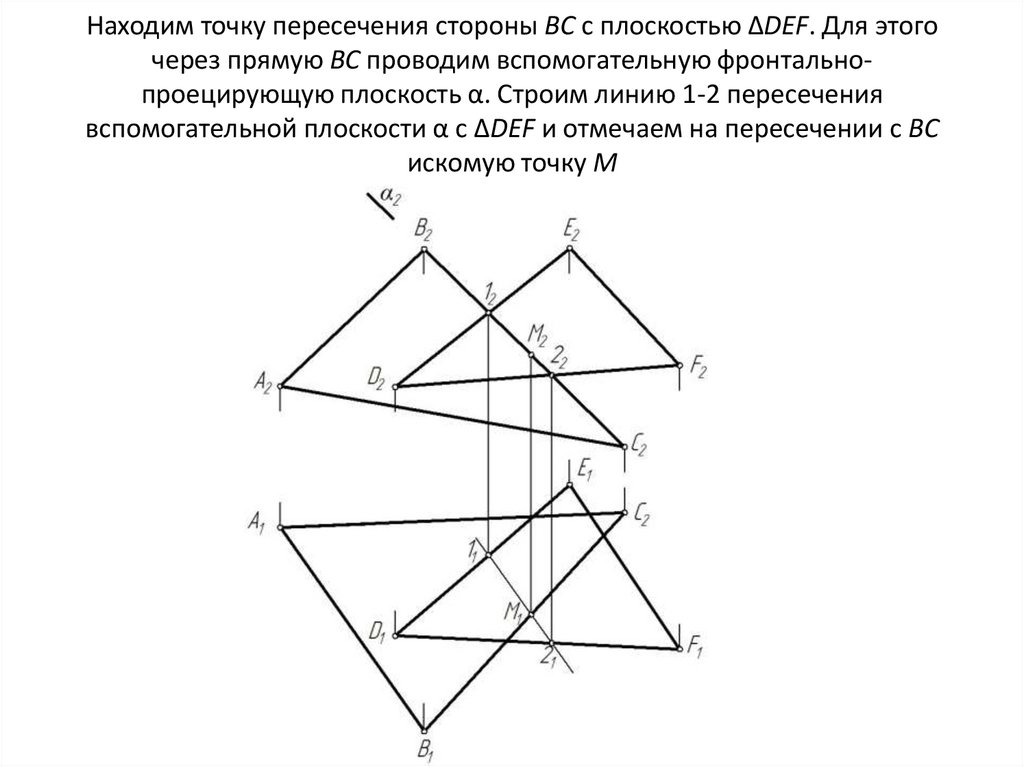
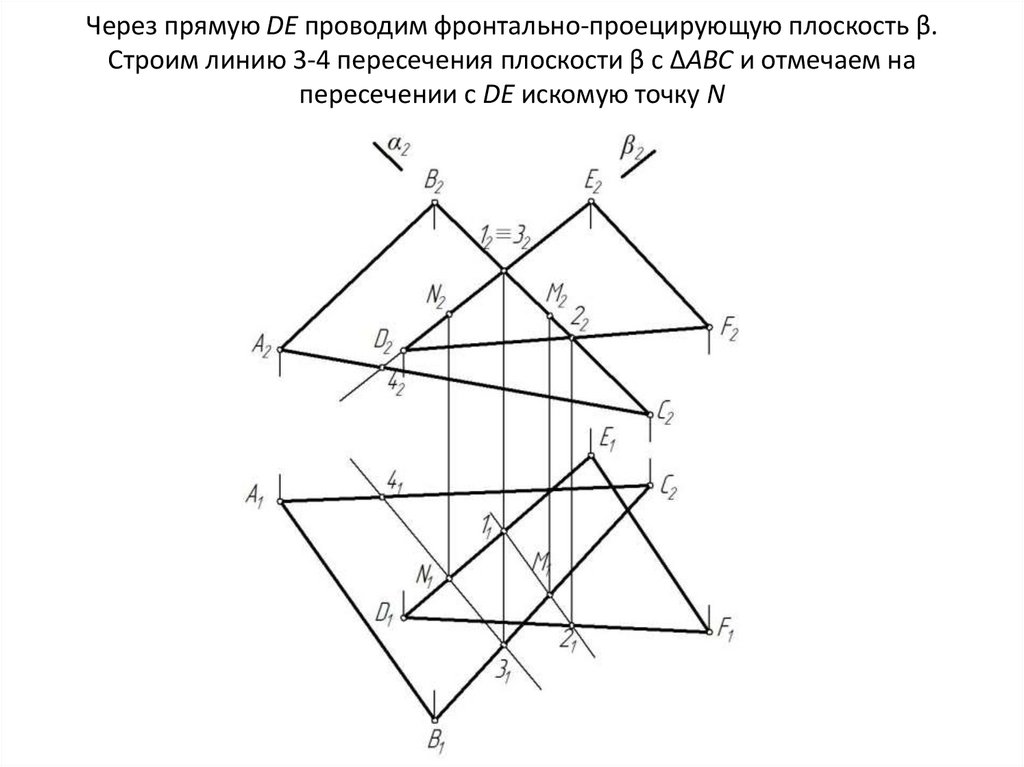
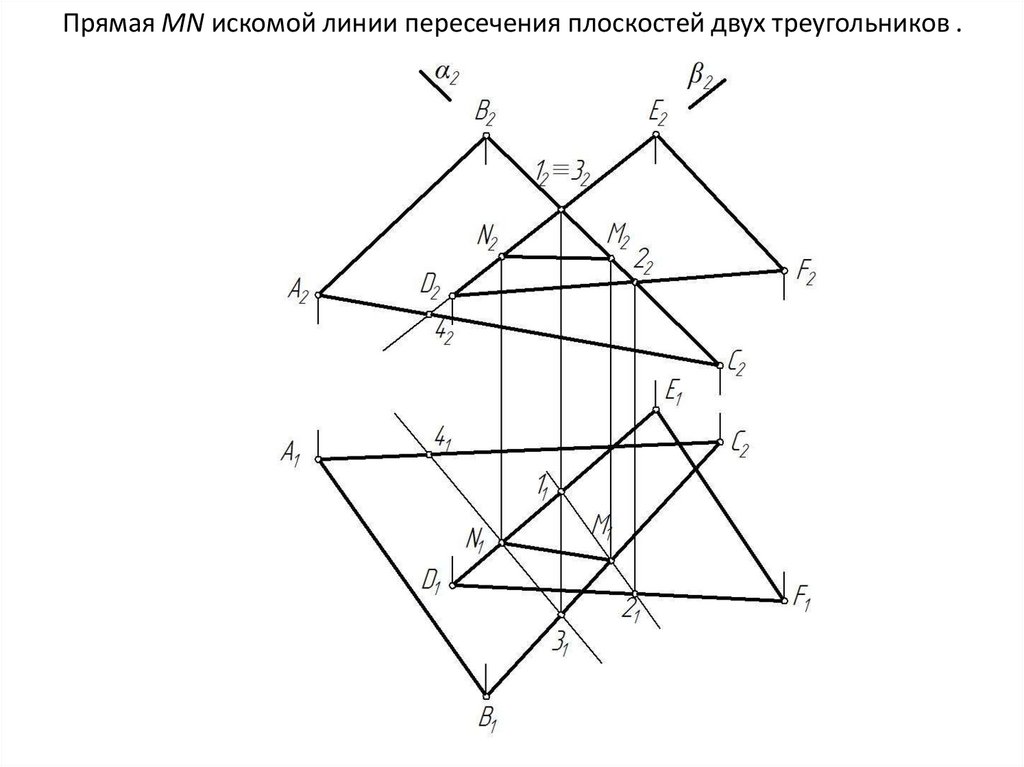
• Построить линию пересечения ΔАВС и ΔDEF17. Находим точку пересечения стороны ВС с плоскостью ΔDEF. Для этого через прямую ВС проводим вспомогательную
фронтальнопроецирующую плоскость α. Строим линию 1-2 пересечениявспомогательной плоскости α с ΔDEF и отмечаем на пересечении с ВС
искомую точку М



 Инженерная графика
Инженерная графика








