Пересечение прямой и плоскости, двух плоскостей

1. Начертательная геометрия Семинар №6 Пересечение прямой и плоскости, двух плоскостей . Подготовили: Данилова У.Б., Елисеева О.И.

2.

Линией пересечения поверхностей
является линия, принадлежащая обеим
пересекающимся поверхностям
разраб.
Данилова
проверил
Елисеева

3.

Линией пересечения плоскостей
является прямая, принадлежащая
обеим пересекающимся плоскостям
разраб.
Данилова
проверил
Елисеева

4.

Задача 44. Построить линию пересечения плоскостей
Дано:
f0a
a’’=b’’
х
b’
h0a
a’
разраб.
Данилова
проверил
Елисеева

5.

Плоскость a задана следами
Плоскость b задана параллельными прямыми
f0a
a’’=b’’
х
b’
h0a
a’
разраб.
Данилова
проверил
Елисеева

6.

Плоскость a – горизонтально-проецирующая
f0a
a
h0a
разраб.
Данилова
проверил
Елисеева

7.

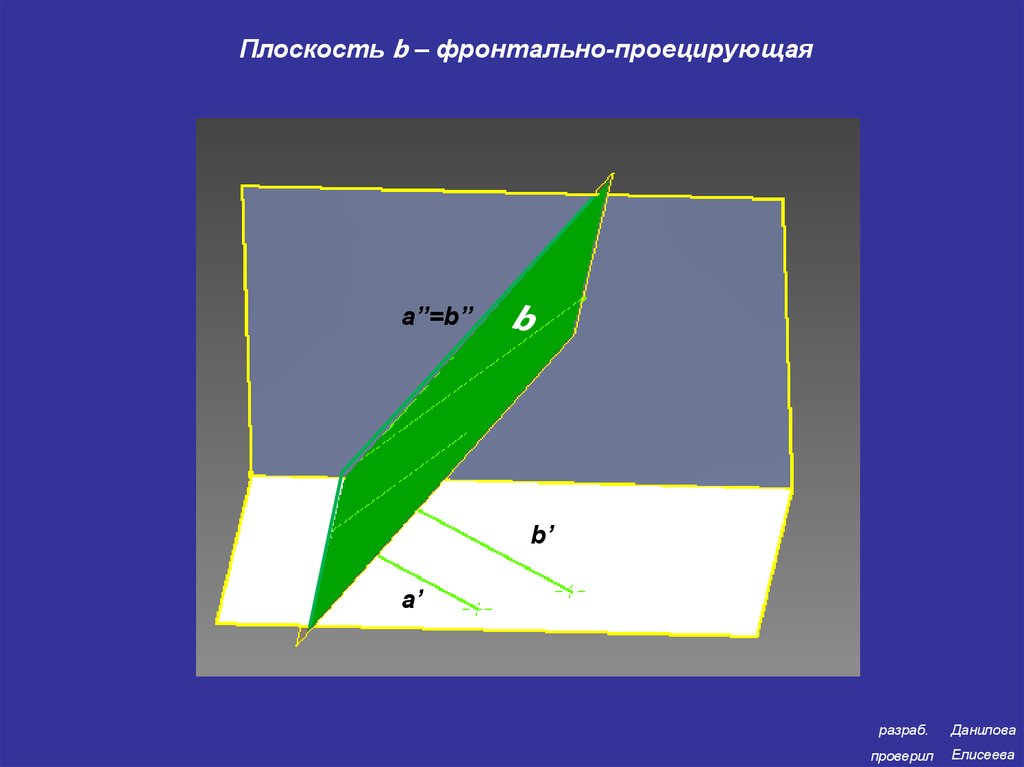
Плоскость b – фронтально-проецирующая
a’’=b’’
b’
a’
разраб.
Данилова
проверил
Елисеева

8.

L- линия пересечения заданных плоскостей
f0a
l’’= a’’=b’’
h0a = l’
b’
a’
разраб.
Данилова
проверил
Елисеева

9.

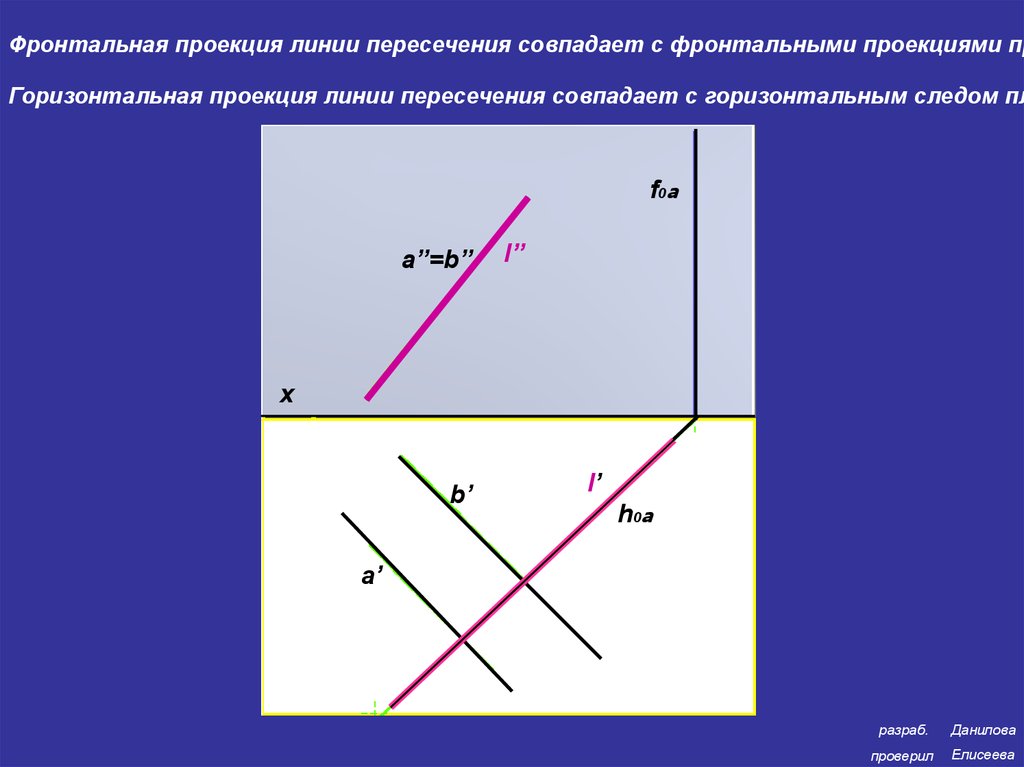
Фронтальная проекция линии пересечения совпадает с фронтальными проекциями пр
Горизонтальная проекция линии пересечения совпадает с горизонтальным следом пл
f0a
a’’=b’’
l’’
х
b’
l’
h0a
a’
разраб.
Данилова
проверил
Елисеева

10.

Задача 44. Построить линию пересечения плоскостей
Дано:
b’’
a’’
f0a
b’’
a’
разраб.
Данилова
проверил
Елисеева

11.

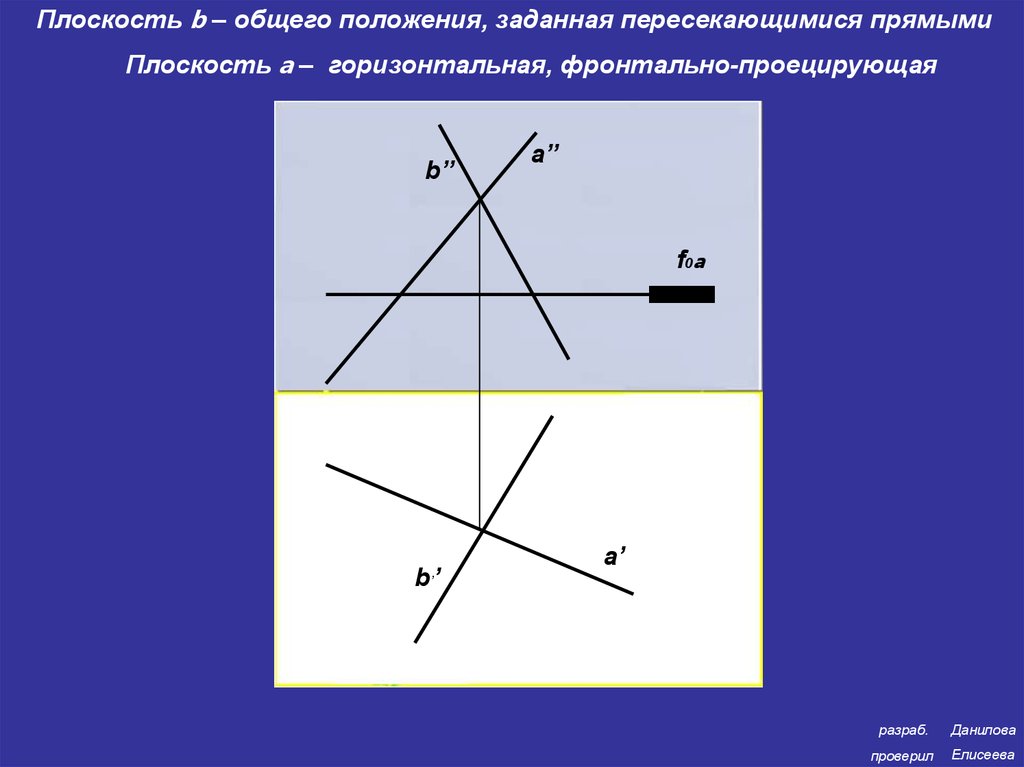
Плоскость b – общего положения, заданная пересекающимися прямыми
Плоскость a – горизонтальная, фронтально-проецирующая
b’’
a’’
f0a
b’’
a’
разраб.
Данилова
проверил
Елисеева

12.

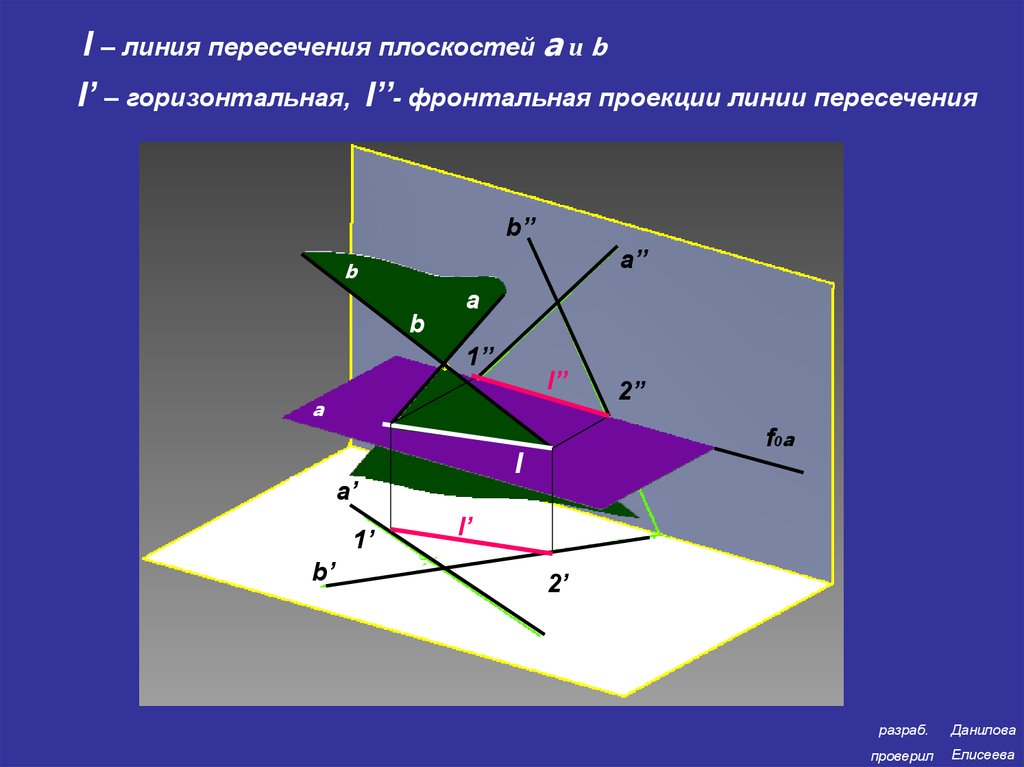
l – линия пересечения плоскостей a и b
l’ – горизонтальная, l’’- фронтальная проекции линии пересечения
b’’
a’’
b
a
b
1’’
l’’
a
2’’
f0a
l
a’
1’
b’
l’
2’
разраб.
Данилова
проверил
Елисеева

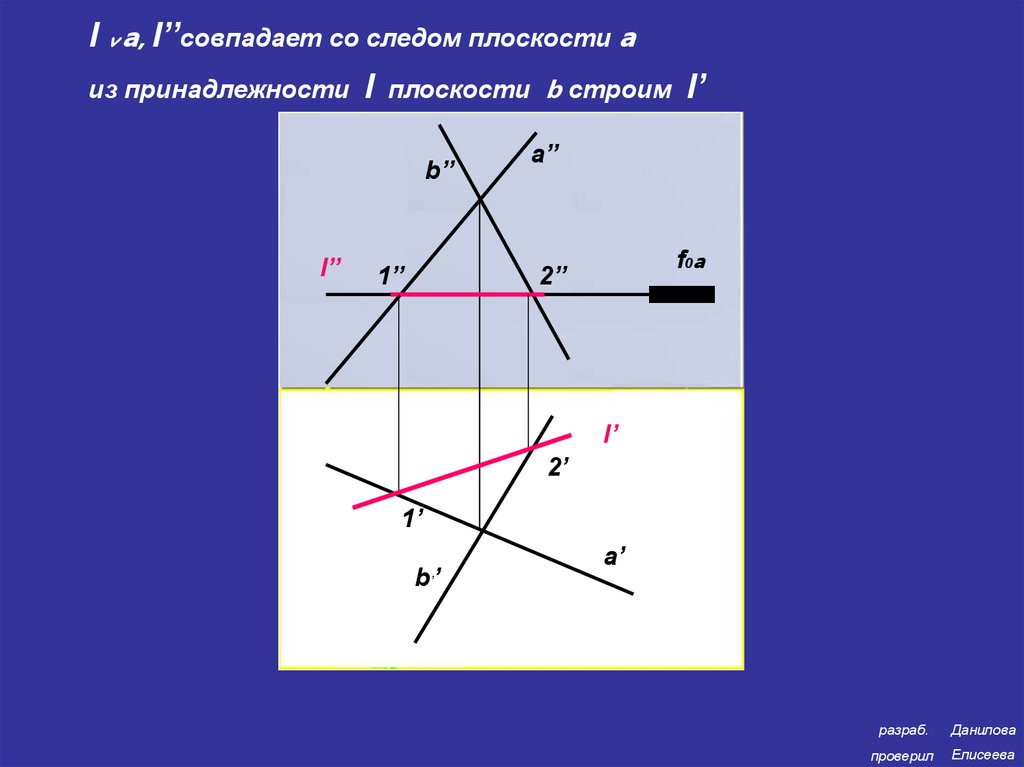
13.

l v a, l’’совпадает со следом плоскости a
из принадлежности
l
плоскости b строим
b’’
l’’
a’’
f0a
2’’
1’’
l’
l’
2’
1’
b’’
a’
разраб.
Данилова
проверил
Елисеева

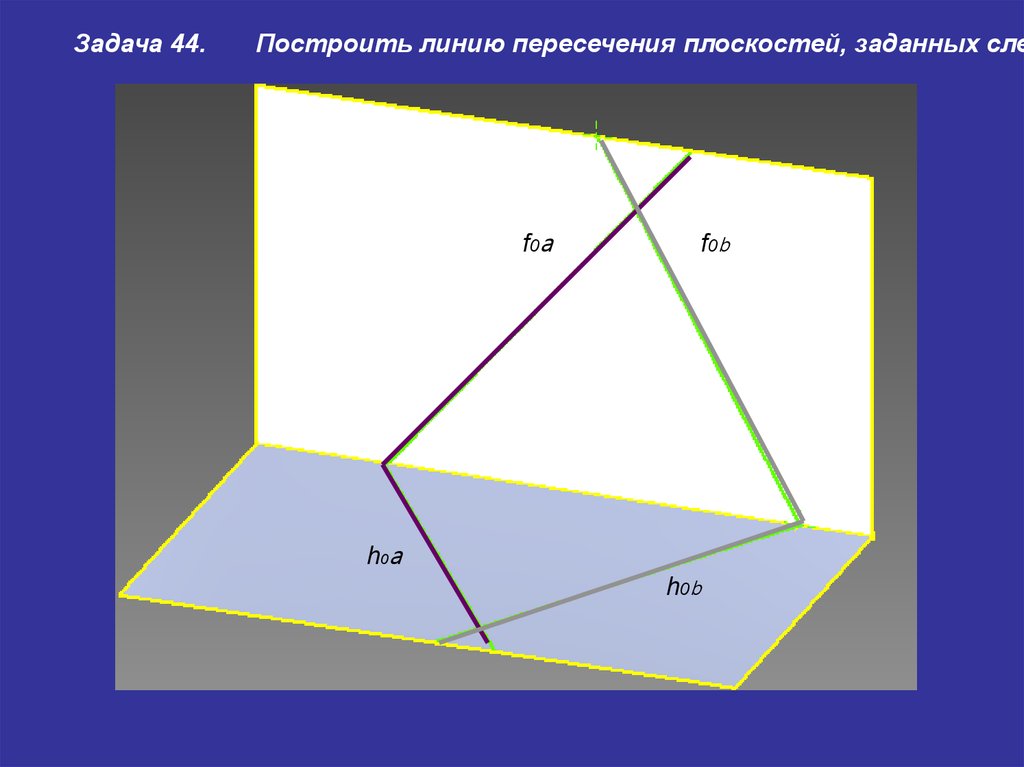
14.

Задача 44.
Построить линию пересечения плоскостей, заданных сле
f0 a
f0 b
h0a
h0b

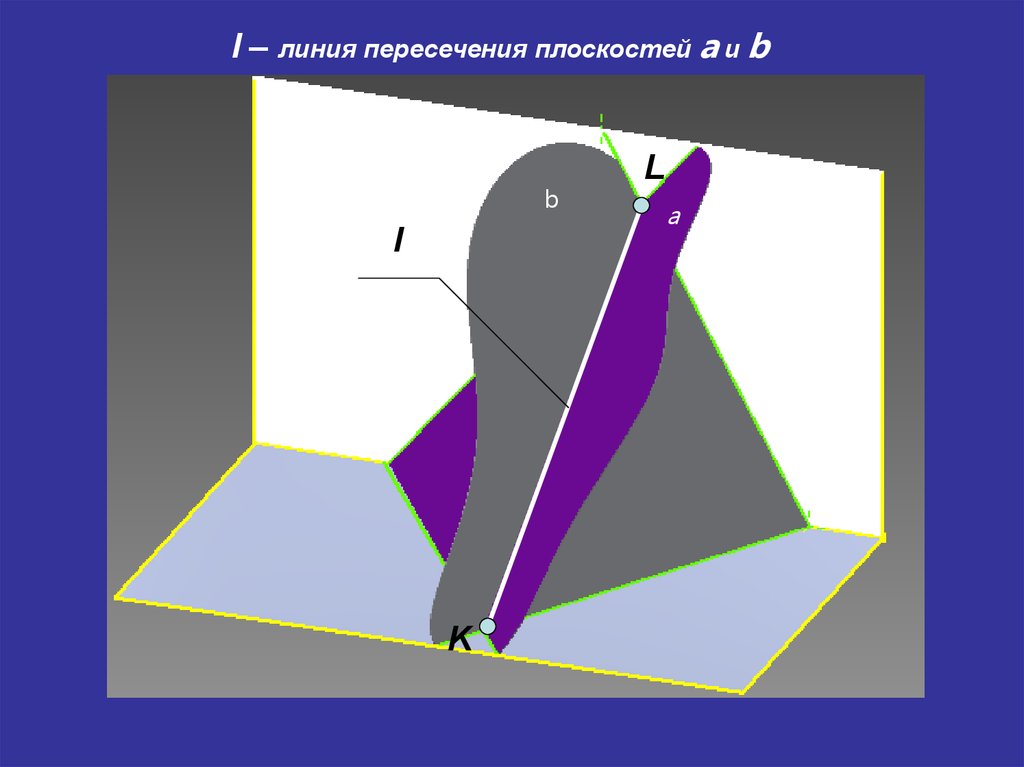
15.

l – линия пересечения плоскостей a и b
b
l
K
L
a

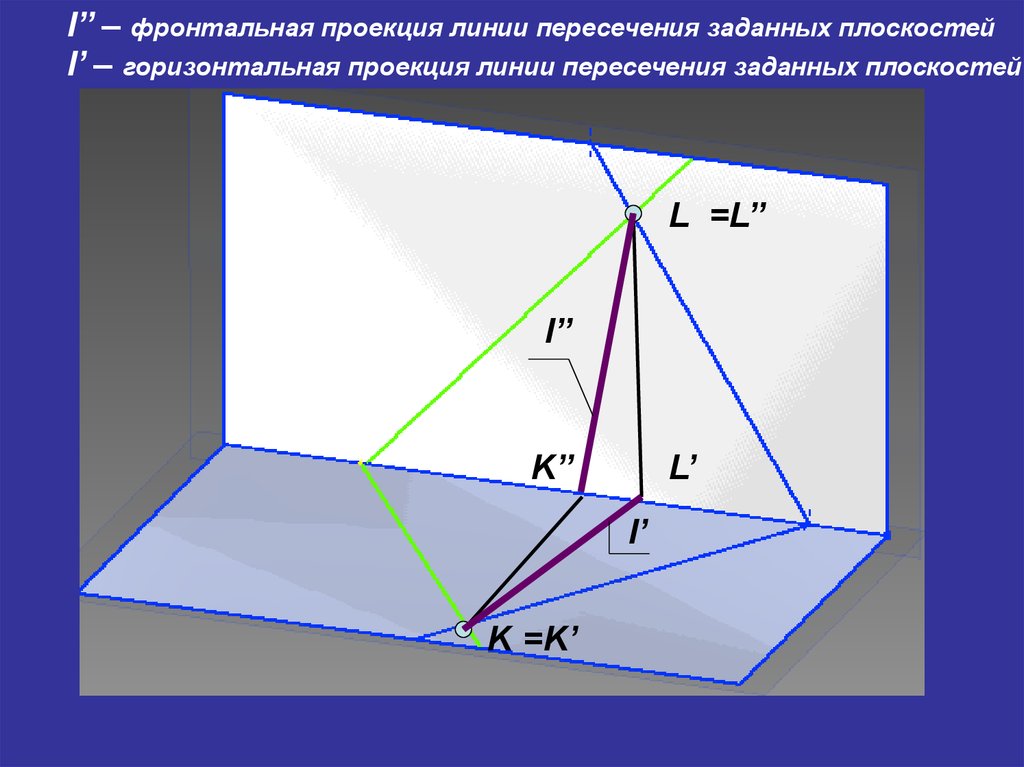
16.

l’’ – фронтальная проекция линии пересечения заданных плоскостей
l’ – горизонтальная проекция линии пересечения заданных плоскостей
L =L’’
l’’
K’’
L’
l’
K =K’

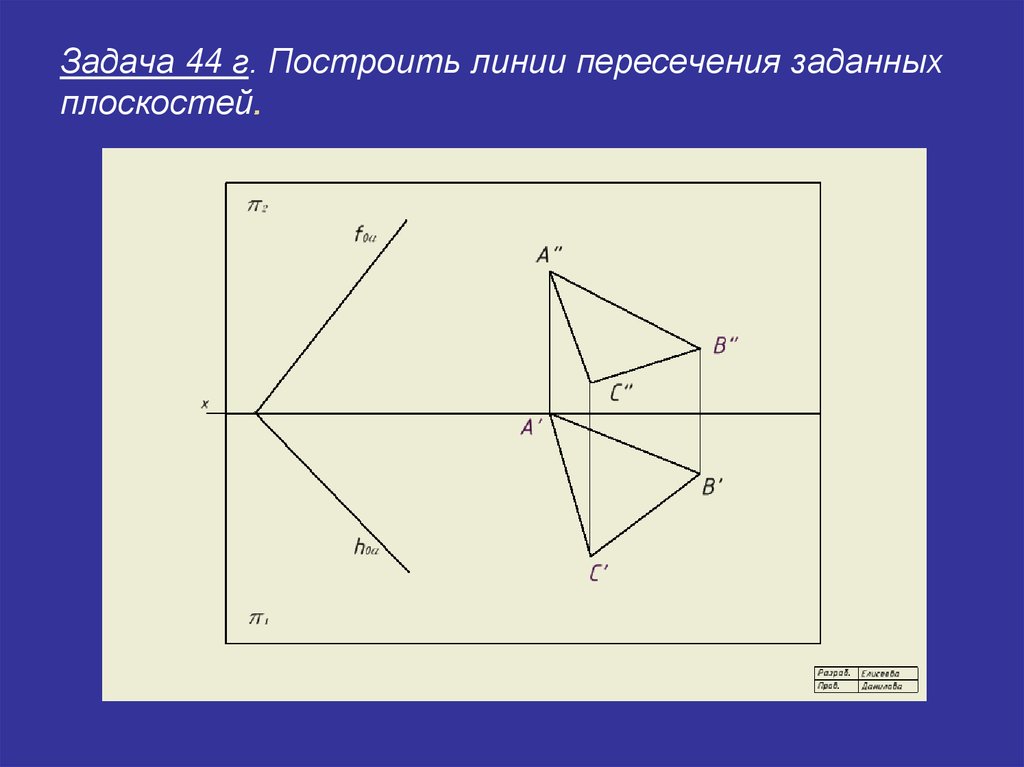
17. Задача 44 г. Построить линии пересечения заданных плоскостей.

Задача 44 г. Построить линии пересечения заданных
плоскостей

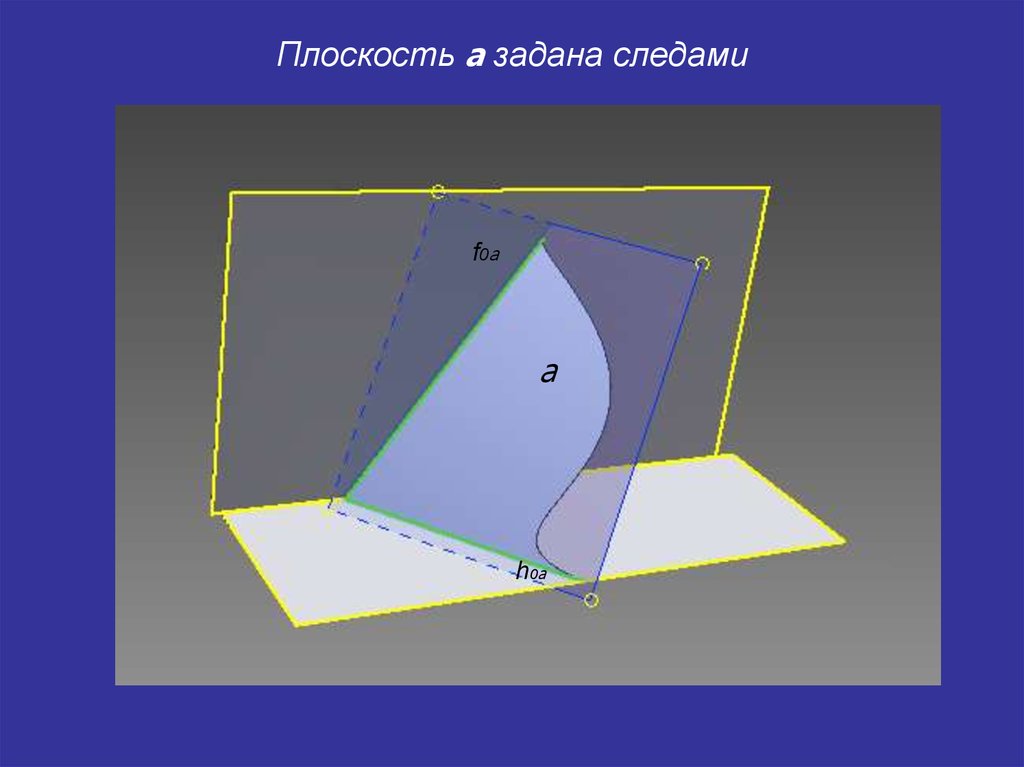
18.

Плоскость a задана следами
f0 a
a
h0a

19.

Плоскость b задана треугольником
p2
A
C
p1
B

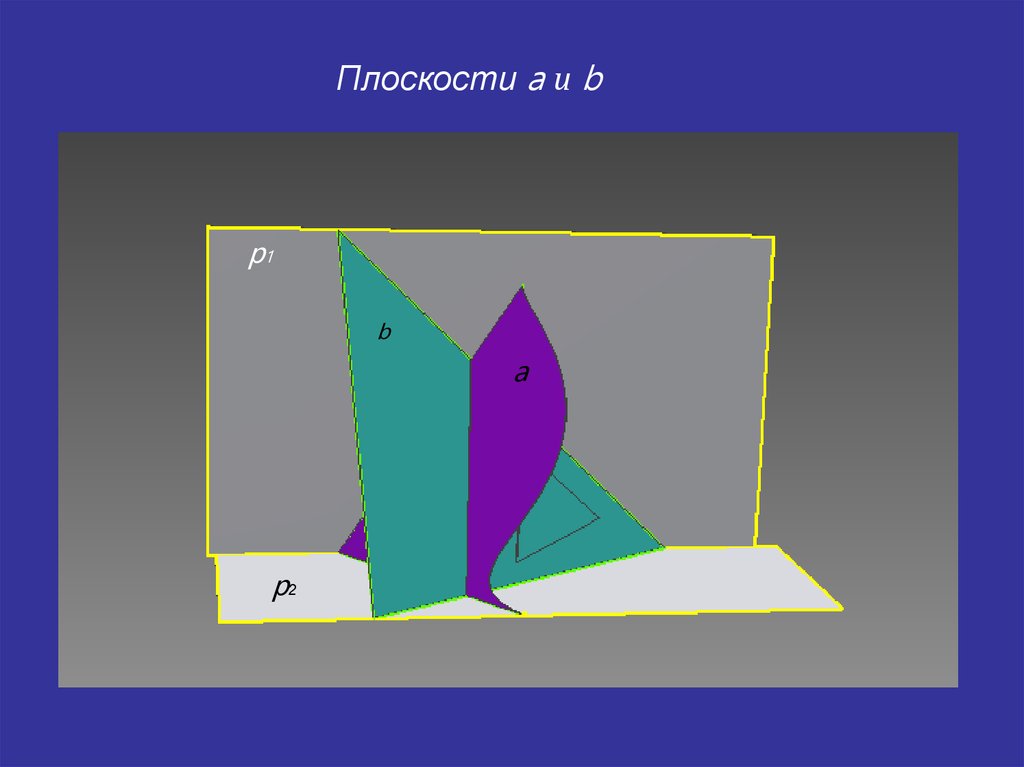
20.

Плоскости a и b
p1
b
a
p2

21.

h1a- горизонталь, принадлежащая плоскости-посреднику g1 и a
h1b - горизонталь, принадлежащая плоскости-посреднику g1
иb
(.)K - точка пересечения горизонталей в плоскости
g1
p1
K
h1 b
h1 a
g1
p2
Горизонтальная плоскость-посредник g1

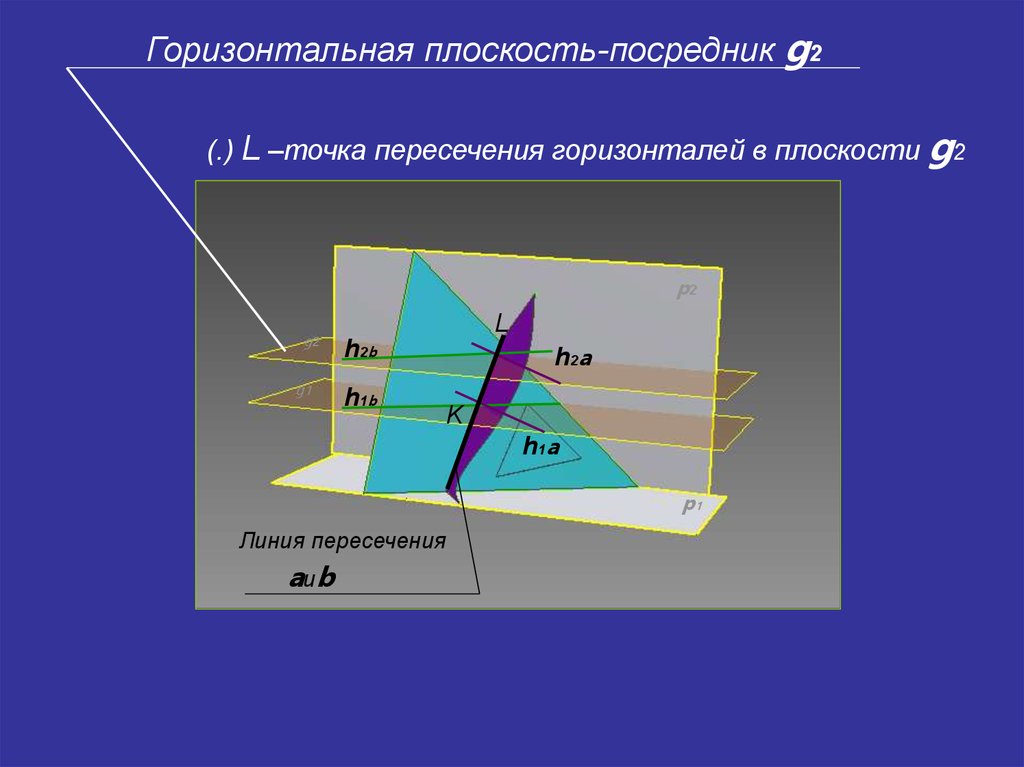
22.

Горизонтальная плоскость-посредник g2
(.) L –точка пересечения горизонталей в плоскости g2
p2
g2
g1
L
h2b
h1b
h2a
K
h1a
p1
Линия пересечения
aиb

23.

Фронтальные плоскости-посредники
g1 и g2
g1
g2

24.

(.)K - точка пересечения фронталей в плоскости
g1
(.) L –точка пересечения фронталей в плоскости
g2
g1
f1a
f2a
f1b
g2
K
f2b
L
Линия пересечения
aи b

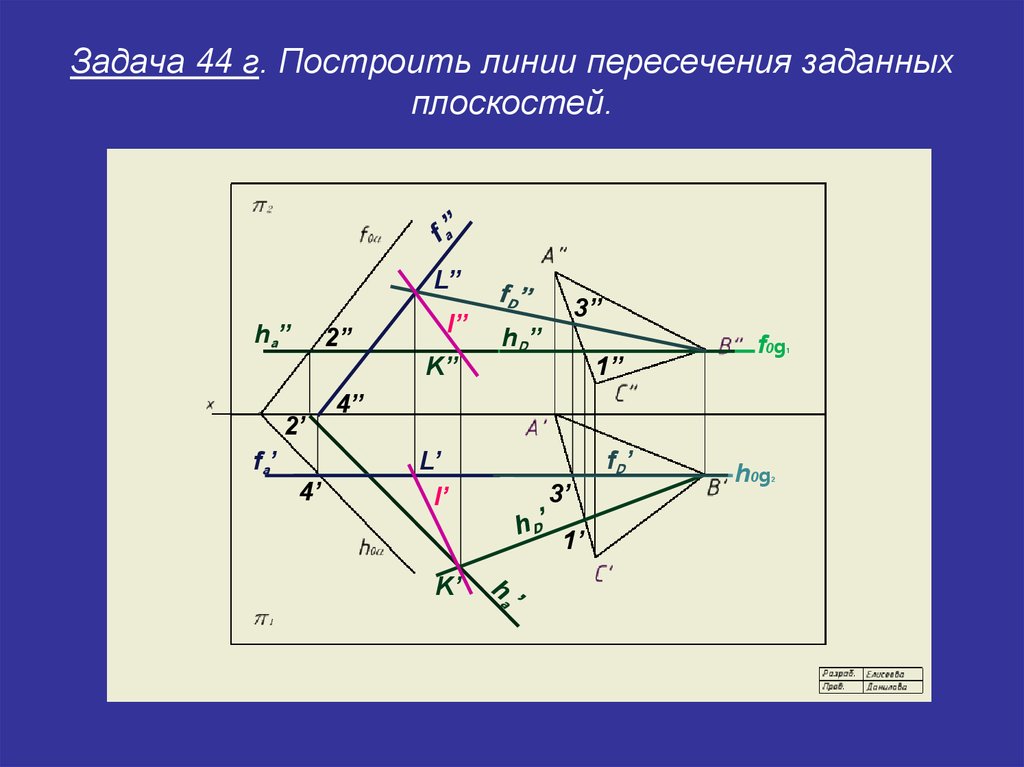
25. Задача 44 г. Построить линии пересечения заданных плоскостей.

L’’
ha’’
2’’
l’’
K’’
2’
f a’
4’
3’’
hD’’
f0g
1
1’’
4’’
L’
l’
fD ’
3’
1’
K’
h0g
2

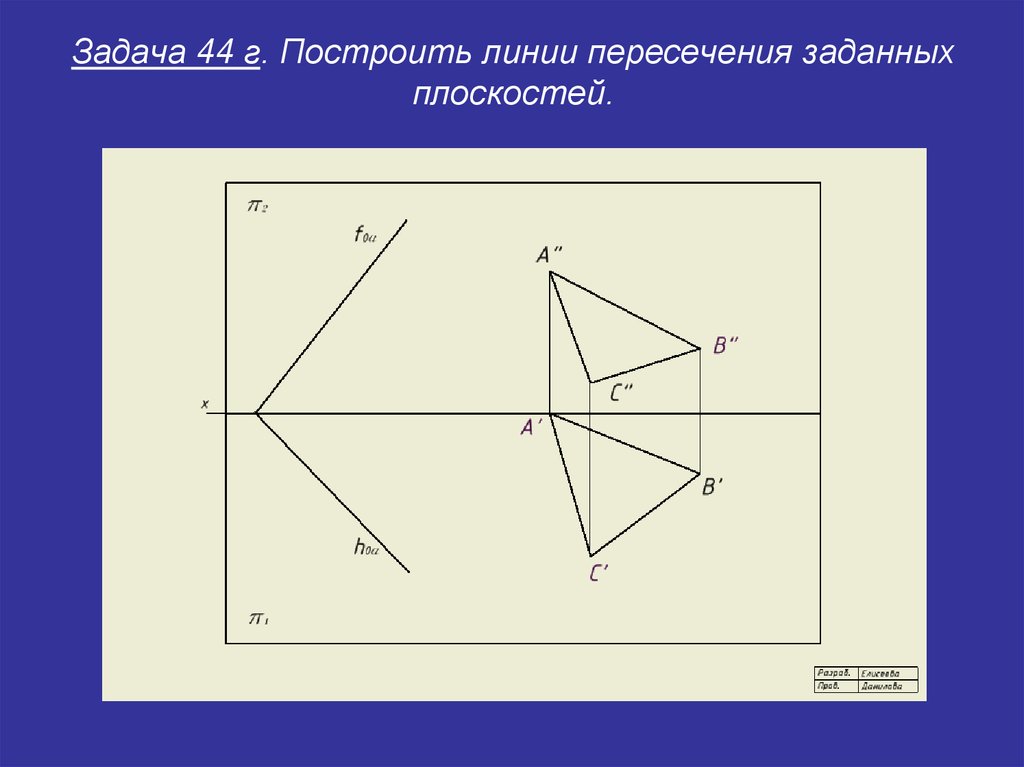
26. Задача 44 г. Построить линии пересечения заданных плоскостей.

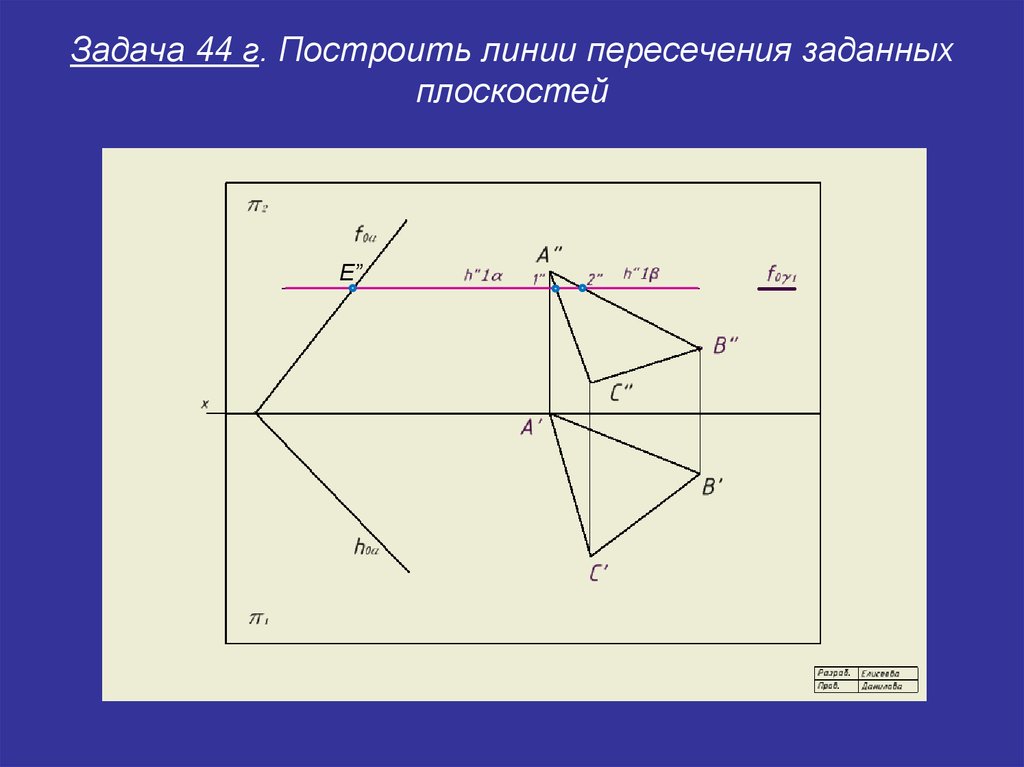
27. Задача 44 г. Построить линии пересечения заданных плоскостей

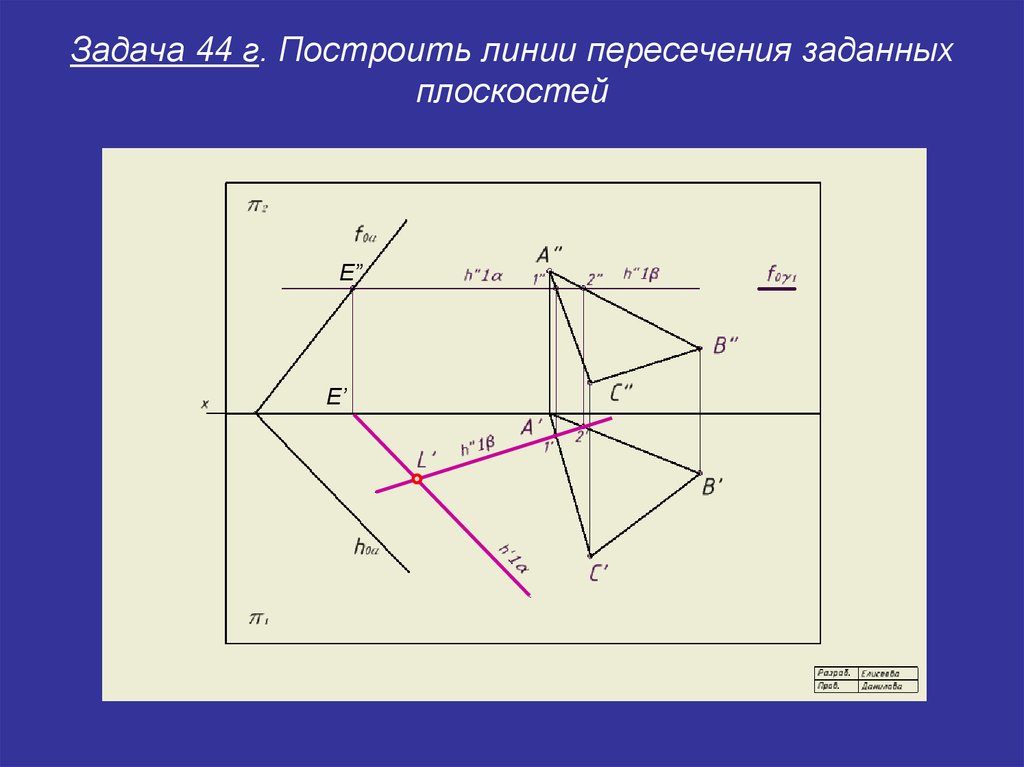
E”

28. Задача 44 г. Построить линии пересечения заданных плоскостей

E”
E’

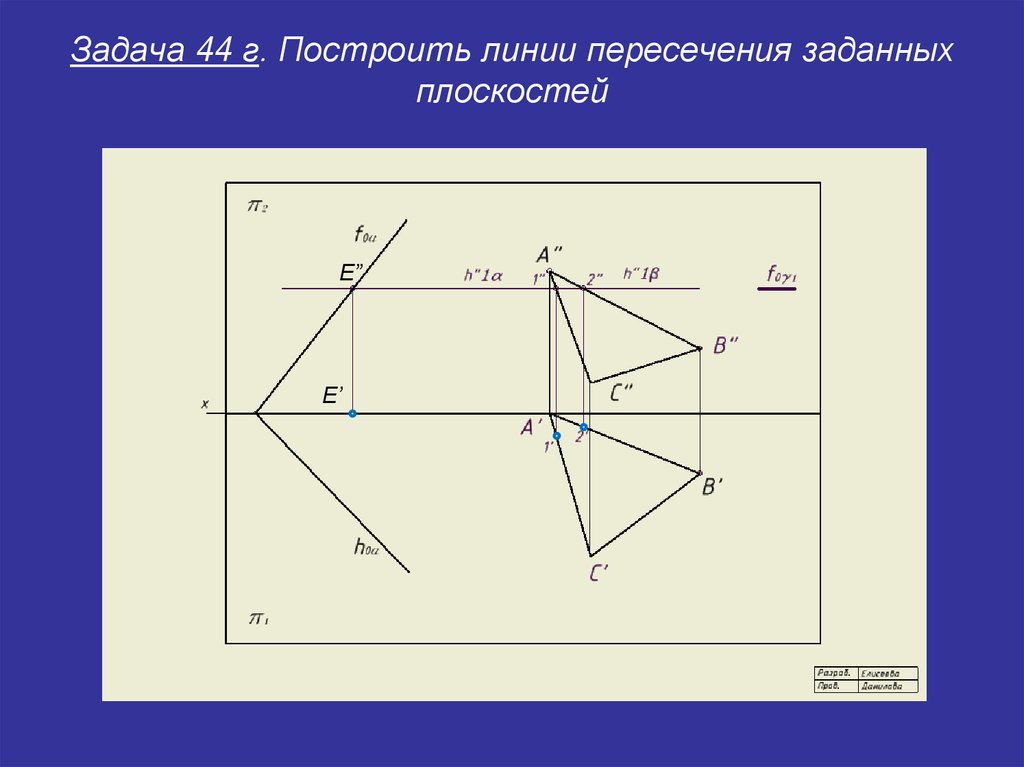
29. Задача 44 г. Построить линии пересечения заданных плоскостей

E”
E’

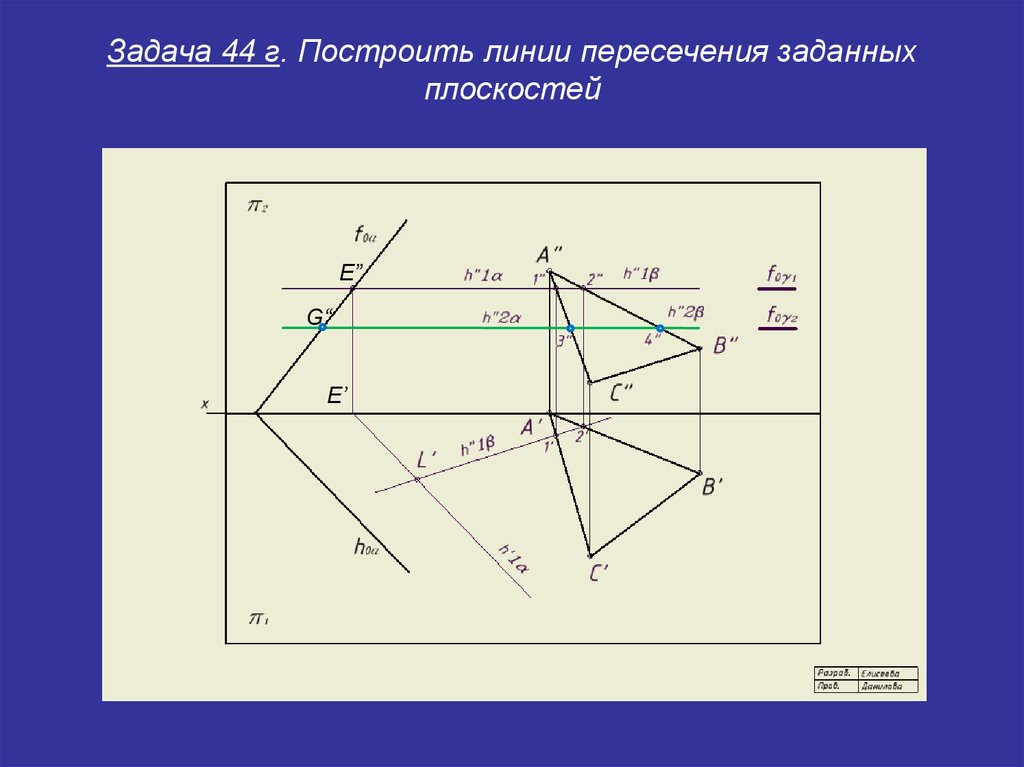
30. Задача 44 г. Построить линии пересечения заданных плоскостей

E”
G“
E’

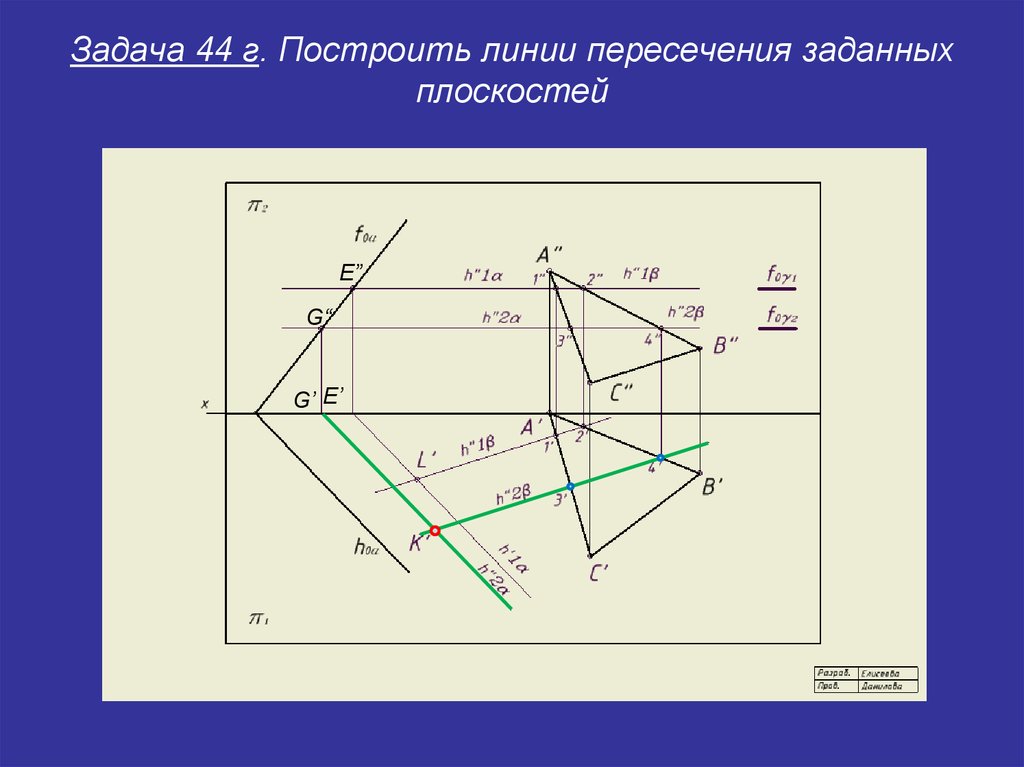
31. Задача 44 г. Построить линии пересечения заданных плоскостей

E”
G“
G’ E’

32. Задача 44 г. Построить линии пересечения заданных плоскостей

33. Задача 44 г. Построить линии пересечения заданных плоскостей

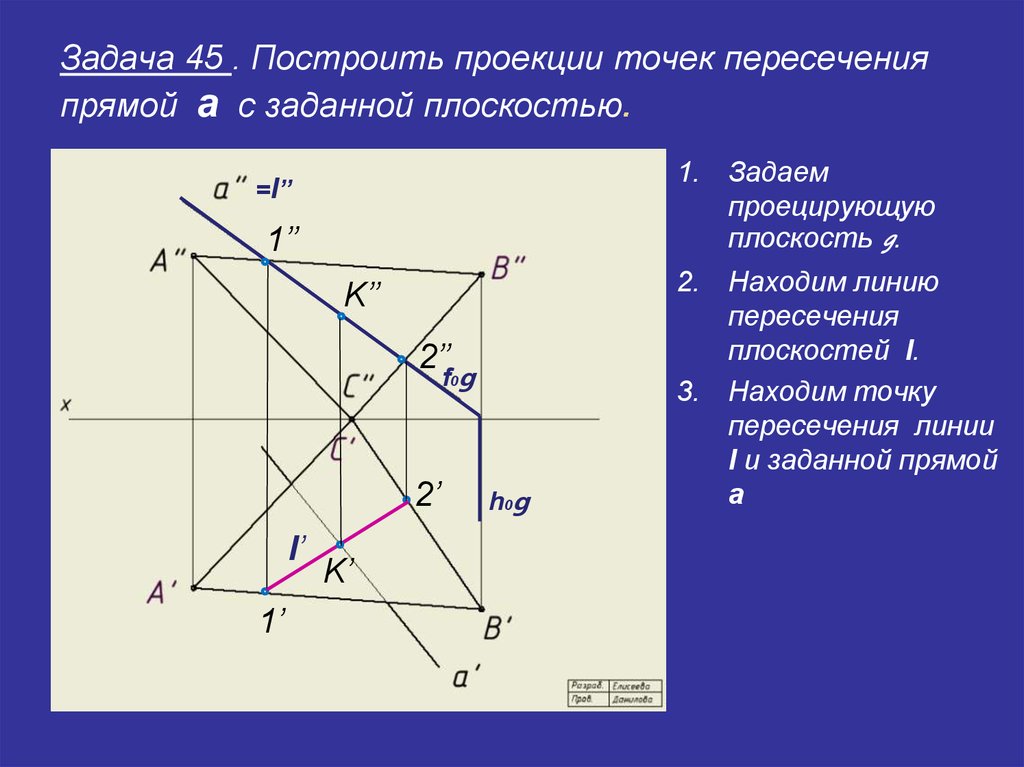
34. Задача 45 . Построить проекции точек пересечения прямой a с заданной плоскостью.

Задача 45 . Построить проекции точек пересечения
прямой a с заданной плоскостью
1. Задаем
проецирующую
плоскость g.
=l’’
1’’
K’’
2’’
f0g
2’
l’
1’
K’
h0g
2. Находим линию
пересечения
плоскостей l.
3. Находим точку
пересечения линии
l и заданной прямой
а

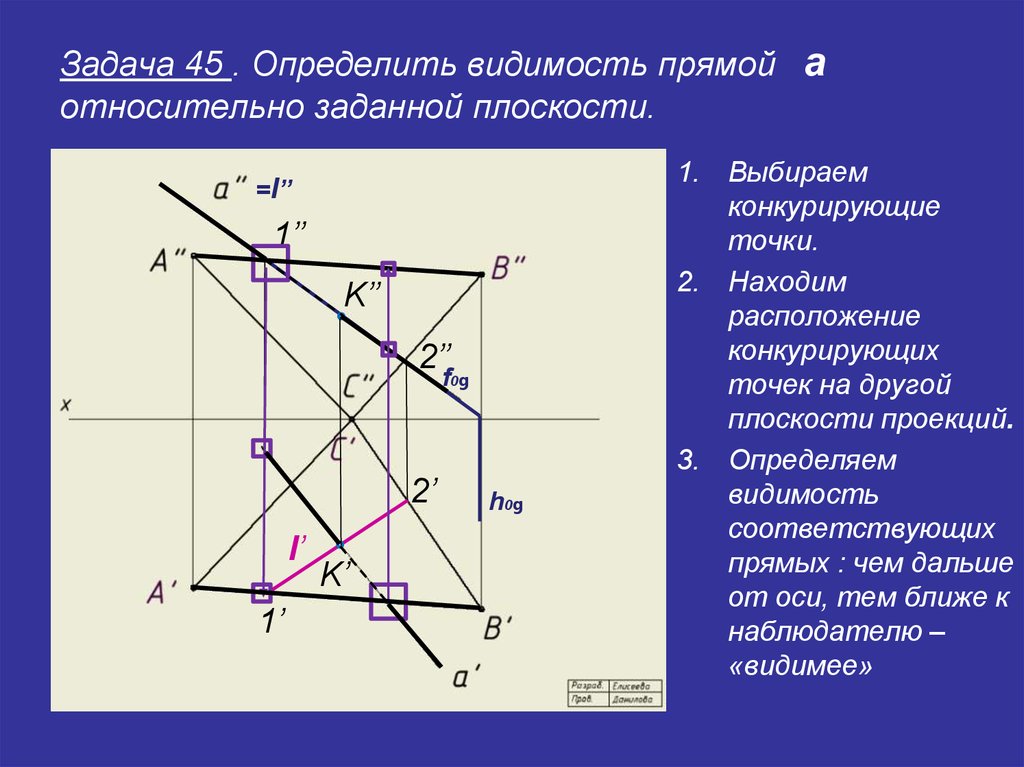
35. Задача 45 . Определить видимость прямой a относительно заданной плоскости.

=l’’
1’’
K’’
2’’
f0g
2’
l’
1’
K’
h0g
1. Выбираем
конкурирующие
точки.
2. Находим
расположение
конкурирующих
точек на другой
плоскости проекций.
3. Определяем
видимость
соответствующих
прямых : чем дальше
от оси, тем ближе к
наблюдателю –
«видимее»

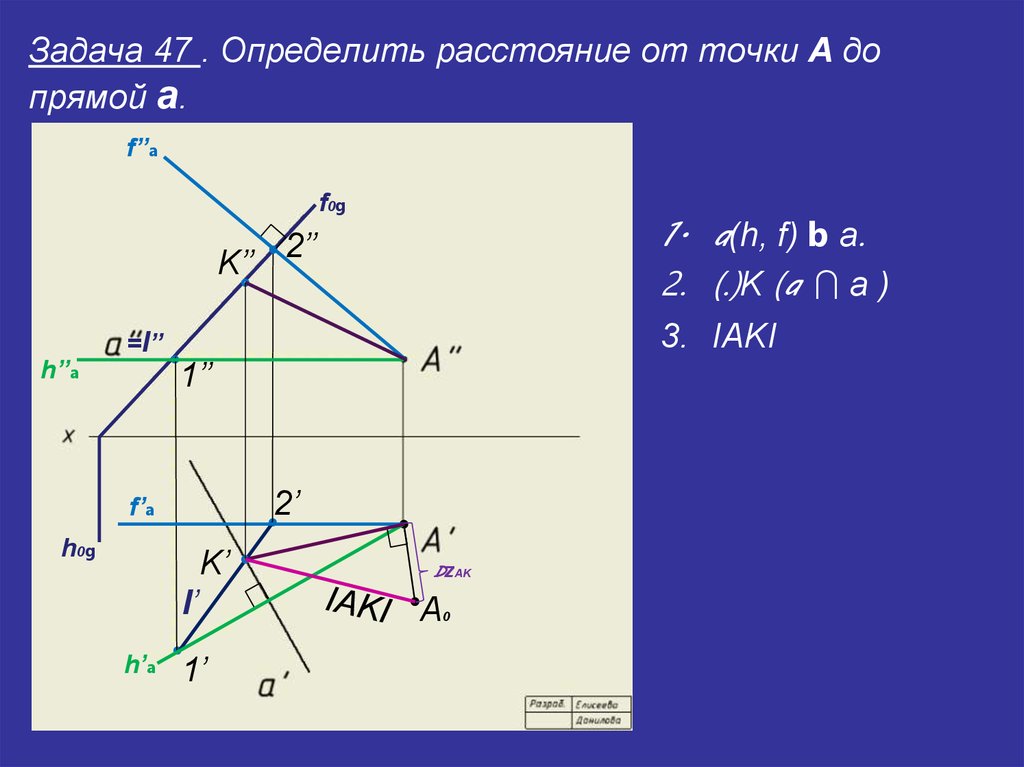
36. Задача 47 . Определить расстояние от точки А до прямой a.

f’’a
f0g
K’’
h’’a
=l’’
3. IAKI
1’’
2’
f’a
h0g
K’
l’
h’a
1. a(h, f) b а.
2. (.)K (a I а )
2’’
1’
DzAK
А
0

37. Задача 48 . Определить расстояние между прямыми a и в.

1. a(а1, в), а1IIа.
f0g
DyAK
А0
А’’
2. Аvа
n’’=l’’
2’’
1’’
K’’
3’’
А’
h0g
3’
K’ l’ 1’
2’
n’
3. n (Аvn, nba)
=h’’a
4. (.)K (a I n)
5. IAKI
=h’a
а1’ =f’a

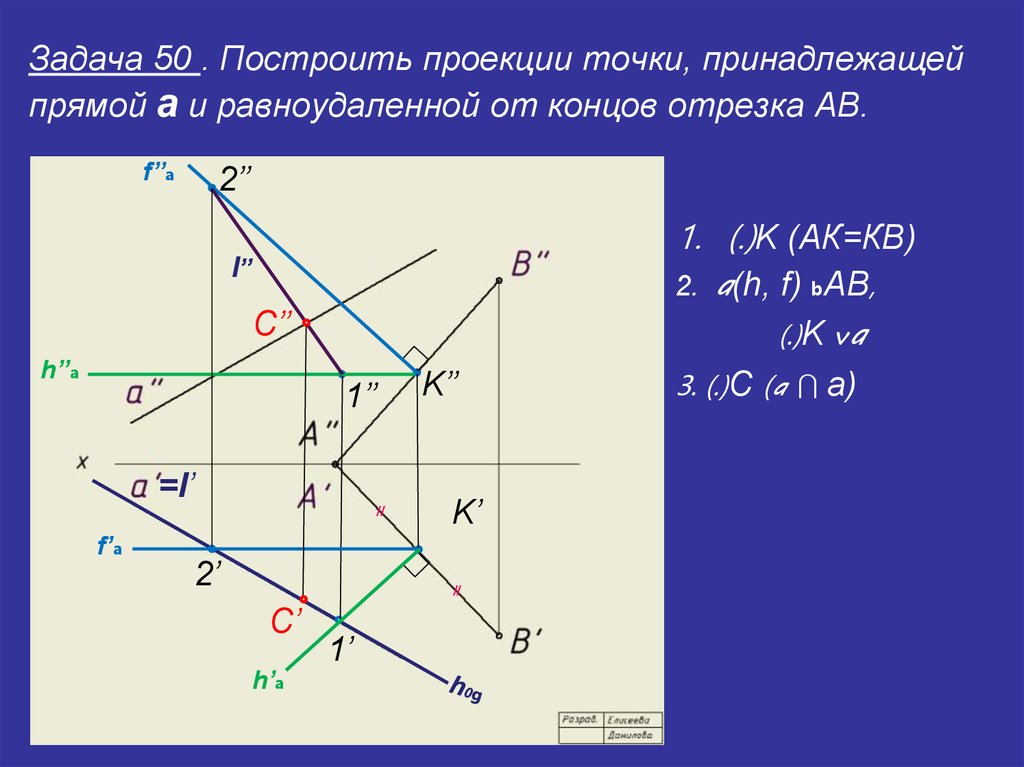
38. Задача 50 . Построить проекции точки, принадлежащей прямой a и равноудаленной от концов отрезка АВ.

f’’a
2’’
1. (.)K (АК=КВ)
2. a(h, f) bAВ,
(.)K va
l’’
С’’
h’’a
1’’
=l’
f’a
II
2’
K’’
K’
II
С’
h’a
1’
3. (.)С (a I а)