Стереометрия. Задание №8

1. ЕГЭ

Стереометрия
Задание № 8

2.

3. Кодификатор

КОДИФИКАТОР
Решать простейшие стереометрические
задачи на нахождение геометрических
величин (длин, углов, площадей, объёмов);
Использовать при решении
стереометрических задач планиметрические
факты и методы

4. Необходимая теория

НЕОБХОДИМАЯ ТЕОРИЯ
Теорема Пифагора
Теорема косинусов
Определение тригонометрических функций в
прямоугольном треугольнике
Формулы площадей поверхностей и объемов
тел
Отношение площадей подобных фигур
Отношение объемов подобных тел

5. Теорема Пифагора

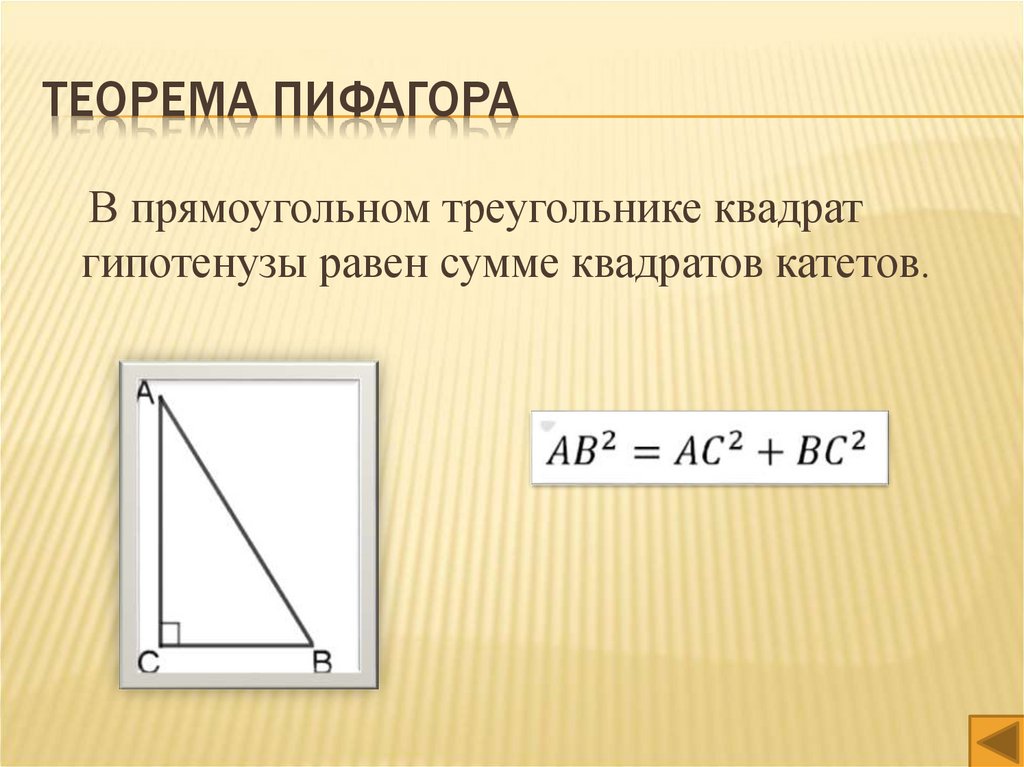
ТЕОРЕМА ПИФАГОРА
В прямоугольном треугольнике квадрат
гипотенузы равен сумме квадратов катетов.

6. Теорема косинусов

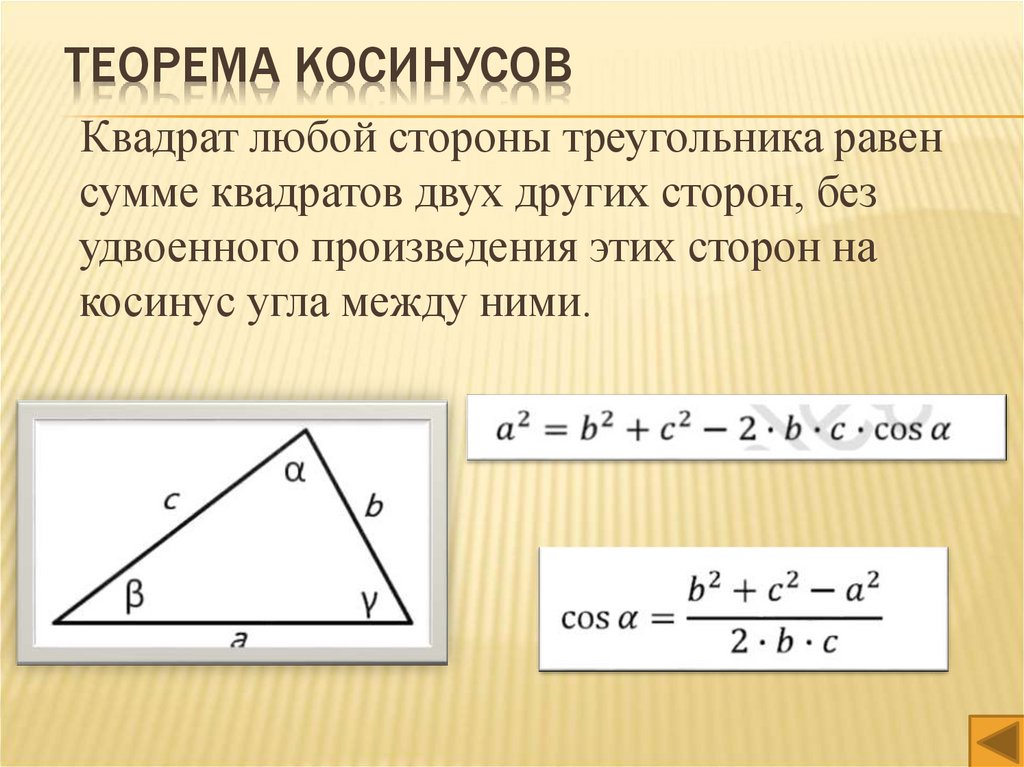
ТЕОРЕМА КОСИНУСОВ
Квадрат любой стороны треугольника равен
сумме квадратов двух других сторон, без
удвоенного произведения этих сторон на
косинус угла между ними.

7. Определение тригонометрических функций в прямоугольном треугольнике

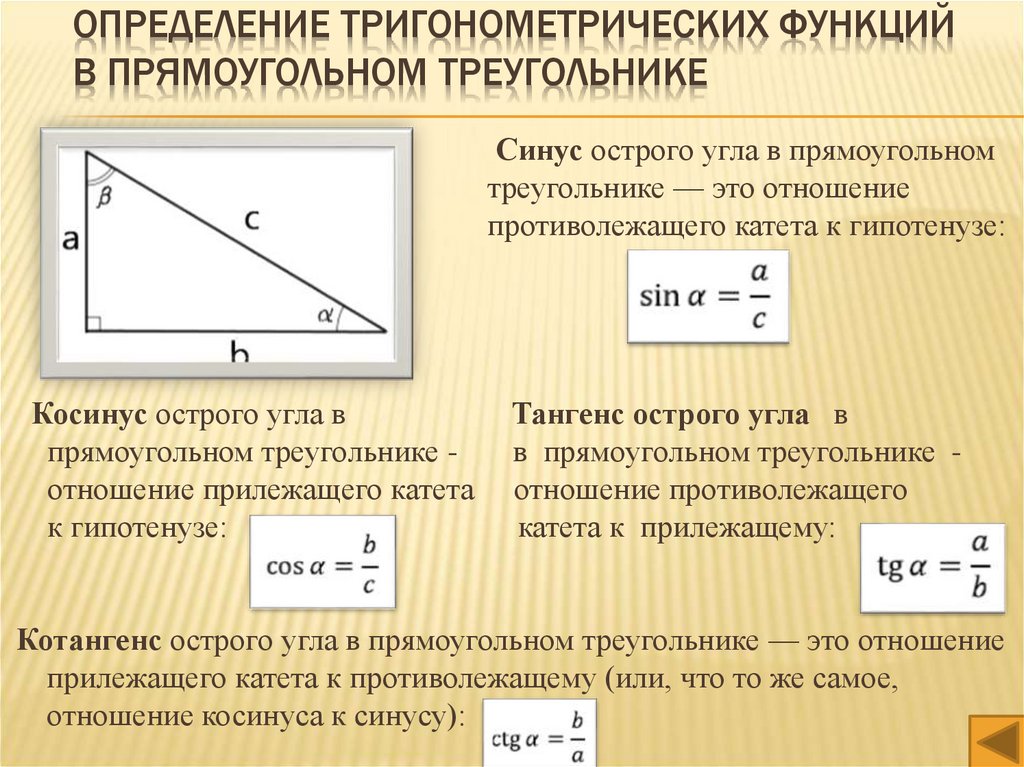
ОПРЕДЕЛЕНИЕ ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЙ
В ПРЯМОУГОЛЬНОМ ТРЕУГОЛЬНИКЕ
Синус острого угла в прямоугольном
треугольнике — это отношение
противолежащего катета к гипотенузе:
Косинус острого угла в
прямоугольном треугольнике отношение прилежащего катета
к гипотенузе:
Тангенс острого угла в
в прямоугольном треугольнике отношение противолежащего
катета к прилежащему:
Котангенс острого угла в прямоугольном треугольнике — это отношение
прилежащего катета к противолежащему (или, что то же самое,
отношение косинуса к синусу):

8.

9.

10.

11.

12. Прототипы заданий №8

ПРОТОТИПЫ ЗАДАНИЙ №8
Многогранники
Куб
Прямоугольный параллелепипед
Составные многогранники
Призма
Пирамида
Тела вращения
Цилиндр
Конус
Сфера и шар
Комбинации тел

13. Куб

КУБ

14.

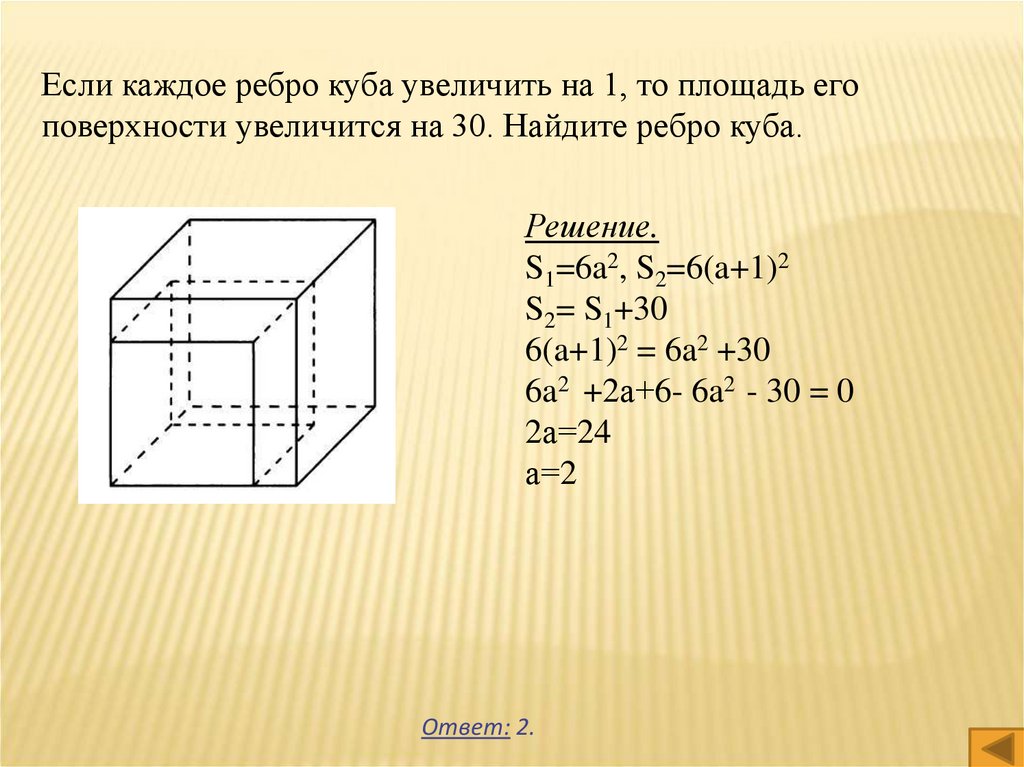
Если каждое ребро куба увеличить на 1, то площадь его
поверхности увеличится на 30. Найдите ребро куба.
Решение.
S1=6a2, S2=6(a+1)2
S2= S1+30
6(a+1)2 = 6a2 +30
6a2 +2а+6- 6a2 - 30 = 0
2а=24
а=2
Ответ: 2.

15. Прямоугольный параллелепипед

ПРЯМОУГОЛЬНЫЙ ПАРАЛЛЕЛЕПИПЕД

16.

Два ребра прямоугольного параллелепипеда, выходящие из одной
вершины, равны 2, 4. Диагональ параллелепипеда равна 6.
Найдите объем параллелепипеда.
Решение
Ответ: 32.

17. Составные многогранники

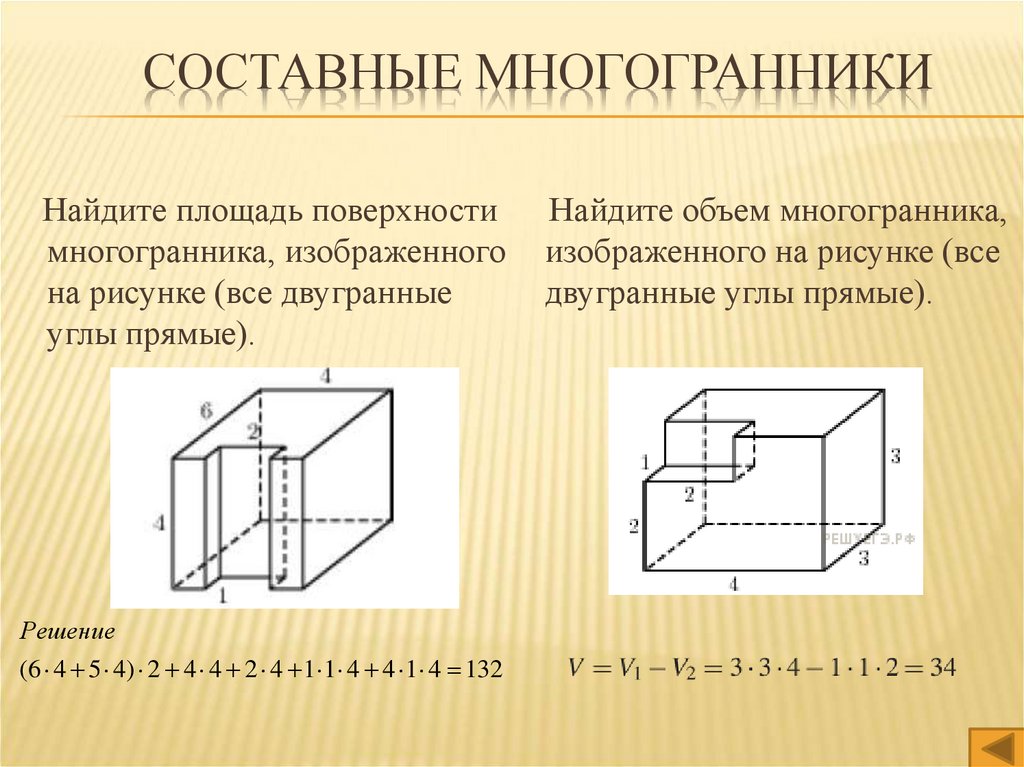
СОСТАВНЫЕ МНОГОГРАННИКИ
Найдите площадь поверхности
многогранника, изображенного
на рисунке (все двугранные
углы прямые).
Решение
(6 4 5 4) 2 4 4 2 4 1 1 4 4 1 4 132
Найдите объем многогранника,
изображенного на рисунке (все
двугранные углы прямые).

18. призма

ПРИЗМА

19.

В правильной шестиугольной призме ABCDEFA1B1C1D1E1F1
все ребра равны 41. Найдите расстояние между точками F и B1.
E1
D1
Решение.
Расстояние между точками
С1 F и B1 найдем из FBB1,
в котором известен катет
BB1 = 41, а катет FB является меньшей
диагональю в правильном шестиугольнике и
равен 41√3. По теореме Пифагора в FBB1 :
FB1 2 = FВ2 + FB12
FB1 2 = (41√3)2 + 412 =
= 412(3 + 1) = 412 ∙ 22;
FB1 = 41 ∙ 2 = 82.
F1
А1
E
В1
D
F
С
А
41
В
Ответ: 82.

20.

В правильной шестиугольной призме ABCDEFA1B1C1D1E1F1
все ребра равны 20. Найдите угол СВЕ. Ответ дайте в градусах.
E1
D1
С1
F1
В1
А1
Решение.
Рассмотрим СВЕ,
в котором известен катет
ВС = 20, а катет ВЕ является большей
диагональю в правильном шестиугольнике
и равен 40.
cos СВЕ = ВС : ВЕ = 20 : 40 = 0,5
СВЕ = 60
D
E
С
F
А
20
В
Ответ: 60.

21. пирамида

ПИРАМИДА

22.

В правильной треугольной пирамиде боковое ребро равно 50,
а сторона основания равна 30√3. Найдите высоту пирамиды.
S
Решение
Основание пирамиды
равносторонний ABC , в котором
50
AB 30 3
30
3
3
В ASО по т. Пифагора
h
AO
А
С
O
30 3
SО 2 SА2 AO 2
SO 2 50 2 30 2 40 2
SO 40.
В
Ответ: 40.

23.

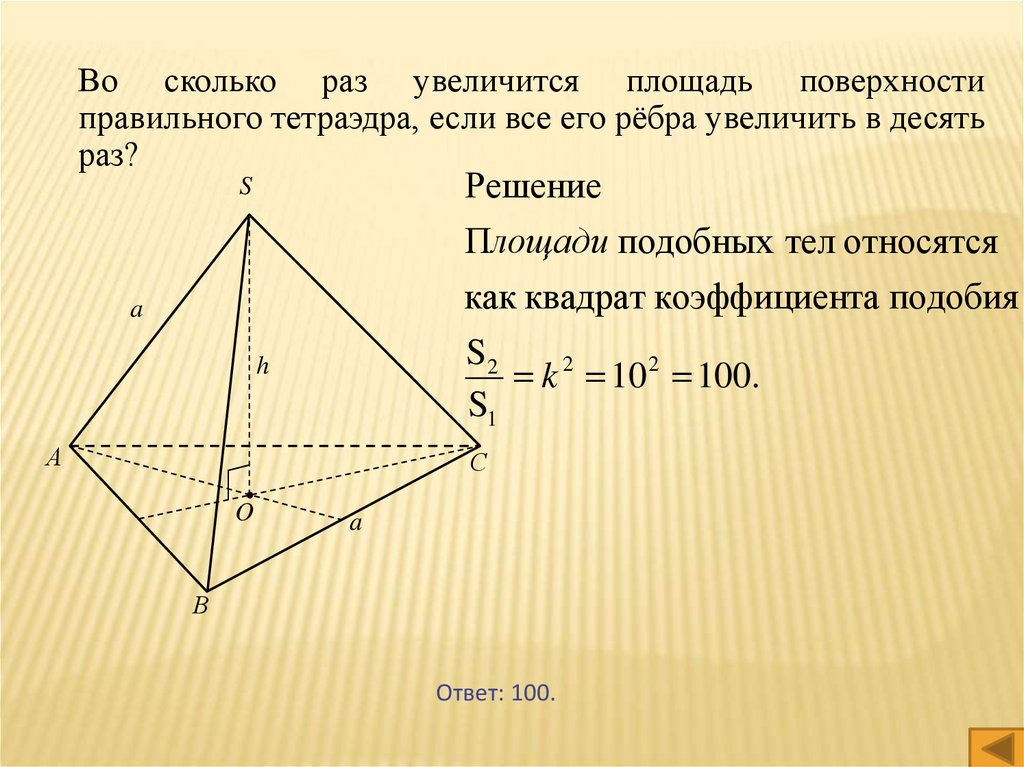
Во сколько раз увеличится площадь поверхности
правильного тетраэдра, если все его рёбра увеличить в десять
раз?
Решение
S
Площади подобных тел относятся
как квадрат коэффициента подобия
a
S2
k 2 10 2 100.
S1
h
А
С
O
a
В
Ответ: 100.

24.

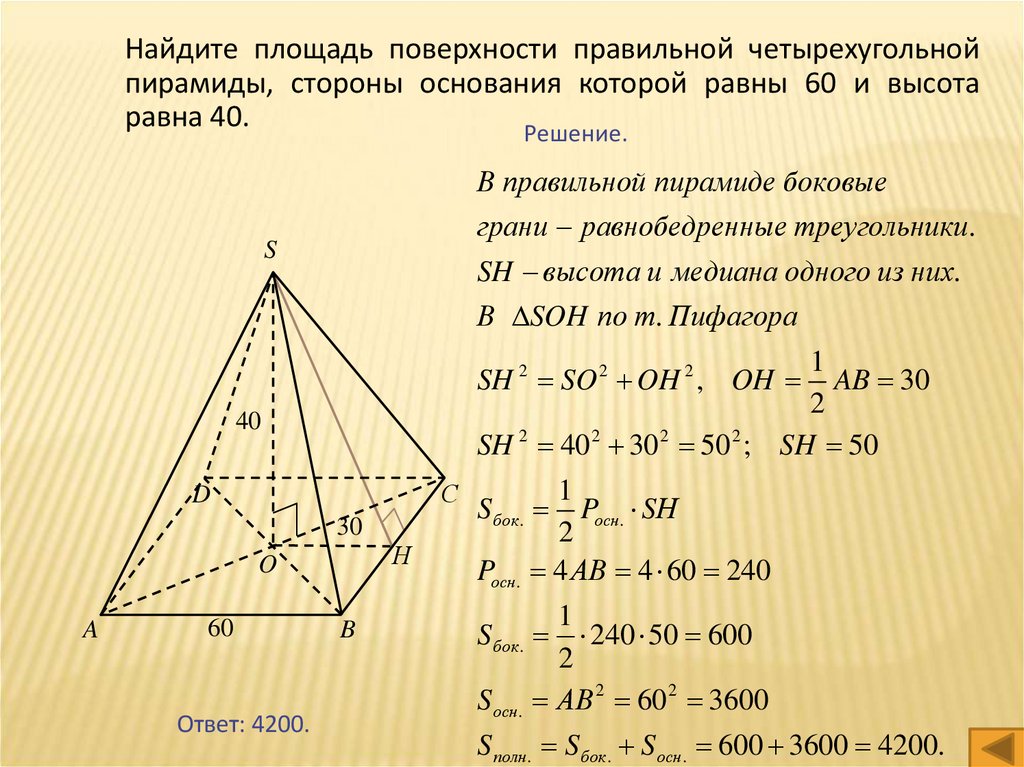
Найдите площадь поверхности правильной четырехугольной
пирамиды, стороны основания которой равны 60 и высота
равна 40.
Решение.
В правильной пирамиде боковые
грани равнобедренные треугольники.
S
SH высота и медиана одного из них.
В SOH по т. Пифагора
1
AB 30
2
SH 2 40 2 30 2 50 2 ; SH 50
SH 2 SO 2 OH 2 , OH
40
С
D
30
Н
O
A
60
Ответ: 4200.
B
1
S бок . Pосн. SН
2
Pосн. 4 АВ 4 60 240
1
S бок . 240 50 600
2
S осн. АВ 2 60 2 3600
S полн. S бок . S осн. 600 3600 4200.

25.

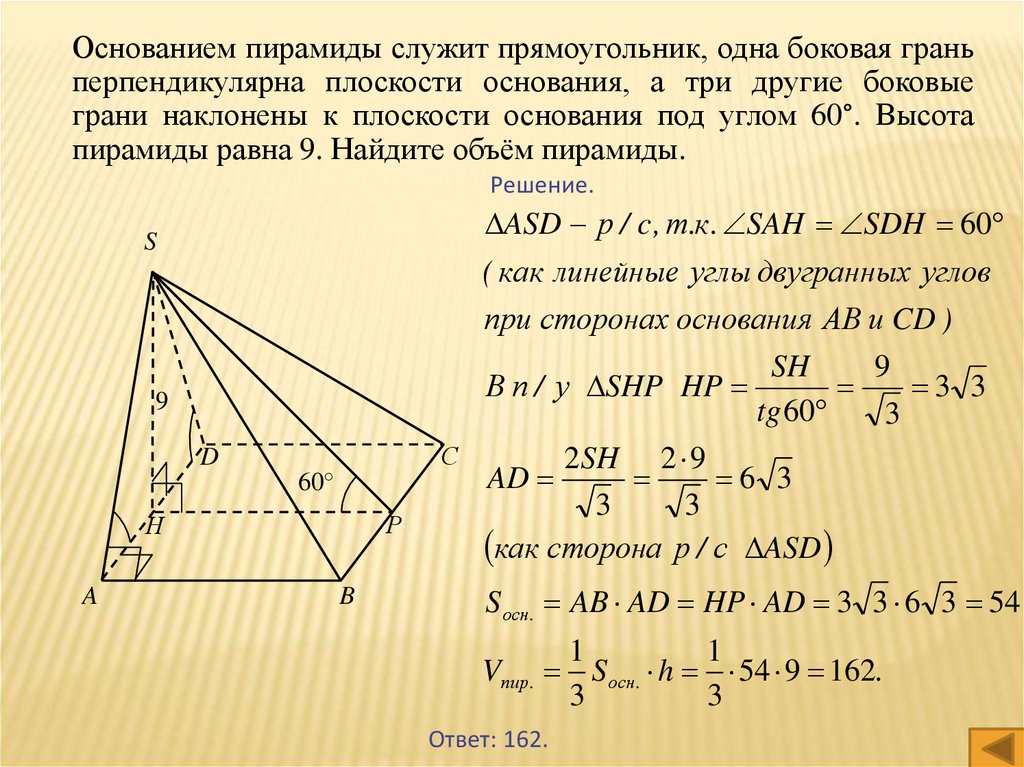
Основанием пирамиды служит прямоугольник, одна боковая грань
перпендикулярна плоскости основания, а три другие боковые
грани наклонены к плоскости основания под углом 60°. Высота
пирамиды равна 9. Найдите объём пирамиды.
Решение.
ASD р / c , т.к . SAH SDH 60
S
( как линейные углы двугранных углов
при сторонах основания АВ и CD )
В п / у SHP HP
9
С
D
60°
Р
Н
A
B
SH
9
3 3
tg 60
3
2 SH 2 9
6 3
3
3
как сторона р / с ASD
AD
S осн . AB AD HP AD 3 3 6 3 54
1
1
Vпир . S осн . h 54 9 162.
3
3
Ответ: 162.

26.

Боковые ребра треугольной пирамиды взаимно перпендикулярны,
каждое из них равно 30. Найдите объём пирамиды.
S
Решение.
Повернем пирамиду на одну из
30
боковых граней так, что боковое
ребро станет высотой пирамиды
А
С
O
С
В
1
Vпир. S осн. h
3
В SAB
Vпир.2
S
А
1
1
SB SA 30 30 450
2
2
1
450 30 4500.
3
S осн.
В
Ответ: 4500.

27.

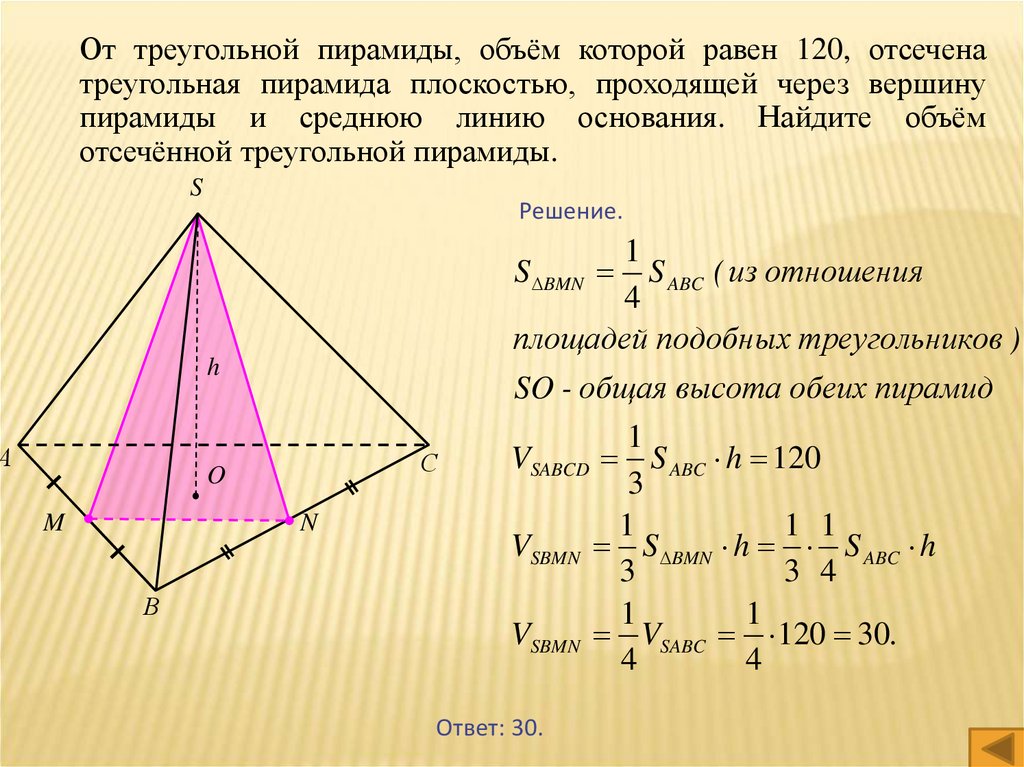
От треугольной пирамиды, объём которой равен 120, отсечена
треугольная пирамида плоскостью, проходящей через вершину
пирамиды и среднюю линию основания. Найдите объём
отсечённой треугольной пирамиды.
S
Решение.
1
S ABC ( из отношения
4
площадей подобных треугольников )
S BMN
h
А
SO - общая высота обеих пирамид
С
O
M
N
В
1
VSABCD S ABC h 120
3
1
1 1
VSBMN S BMN h S ABC h
3
3 4
1
1
VSBMN VSABC 120 30.
4
4
Ответ: 30.

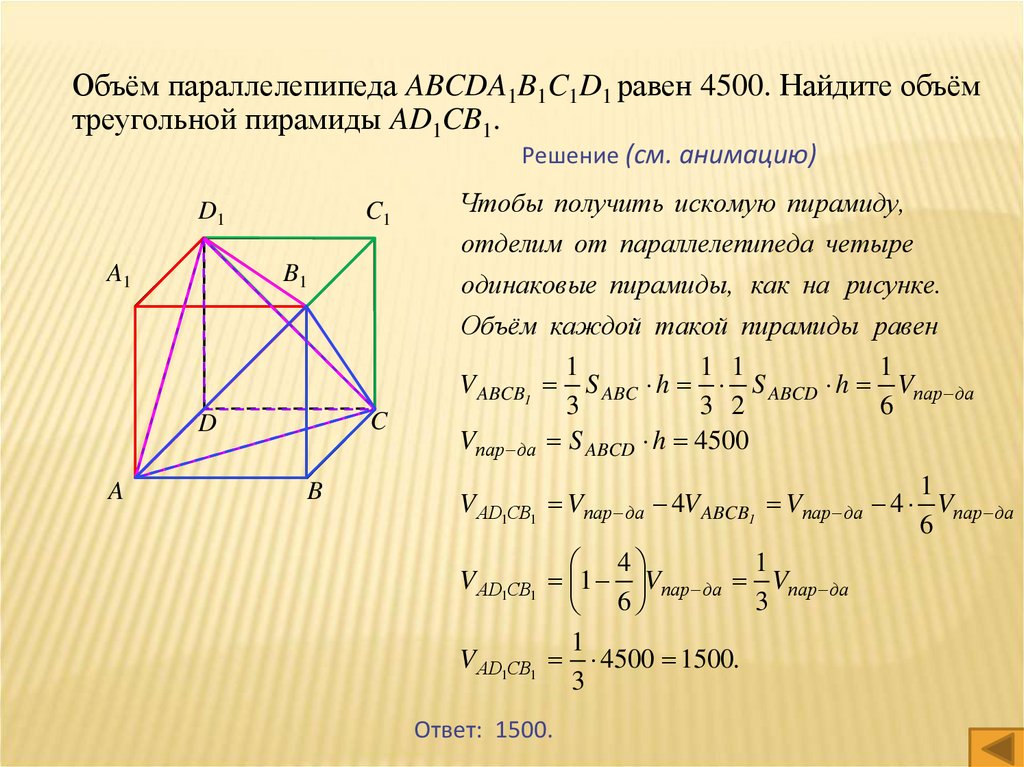
28.

Объём параллелепипеда ABCDA1B1C1D1 равен 4500. Найдите объём
треугольной пирамиды AD1CB1.
Решение (см. анимацию)
D1
A1
C1
B1
Чтобы получить искомую пирамиду,
отделим от параллелепипеда четыре
одинаковые пирамиды, как на рисунке.
Объём каждой такой пирамиды равен
1
1 1
1
S ABC h S ABCD h Vпар да
3
3 2
6
S ABCD h 4500
V ABCB1
C
D
A
B
Vпар да
1
V АD1СВ1 Vпар да 4V ABCB1 Vпар да 4 Vпар да
6
1
4
V АD1СВ1 1 Vпар да Vпар да
3
6
1
V АD1СВ1 4500 1500.
3
Ответ: 1500.

29.

Одна цилиндрическая кружка вдвое выше второй, зато вторая в полтора раза
шире. Найдите отношение объема второй кружки к объему первой.
Решение
Обозначим площадь и высоту второй кружки за S2 и V2.
Тогда объем первой кружки
Ответ 1,125

30.

Диаметр основания конуса равен 14, а длина
образующей - 25. Найдите площадь осевого сечения
этого конуса.
Решение: Осевым сечением конуса
является равнобедренный треугольник,
основание которого диаметр D основания конуса, а
высота h совпадает с высотой конуса.
По условию образующая конуса l = 25,
радиус основания r = D / 2 = 14 / 2 = 7.
Тогда:

31. ПРОБЛЕМНАЯ ЗАДАЧА: При уличной торговле арбузами весы отсутствовали. Однако, выход был найден: арбуз радиусом 3 дм приравнивали

по стоимости к
трём арбузам радиусом 1 дм. Что вы возьмете? Правы ли были продавцы?
R=3 дм
R=1 дм
4
4
4
V R 3 33 27 36
3
3
3
в
> 9 раз
3V 3
4
13 4
3

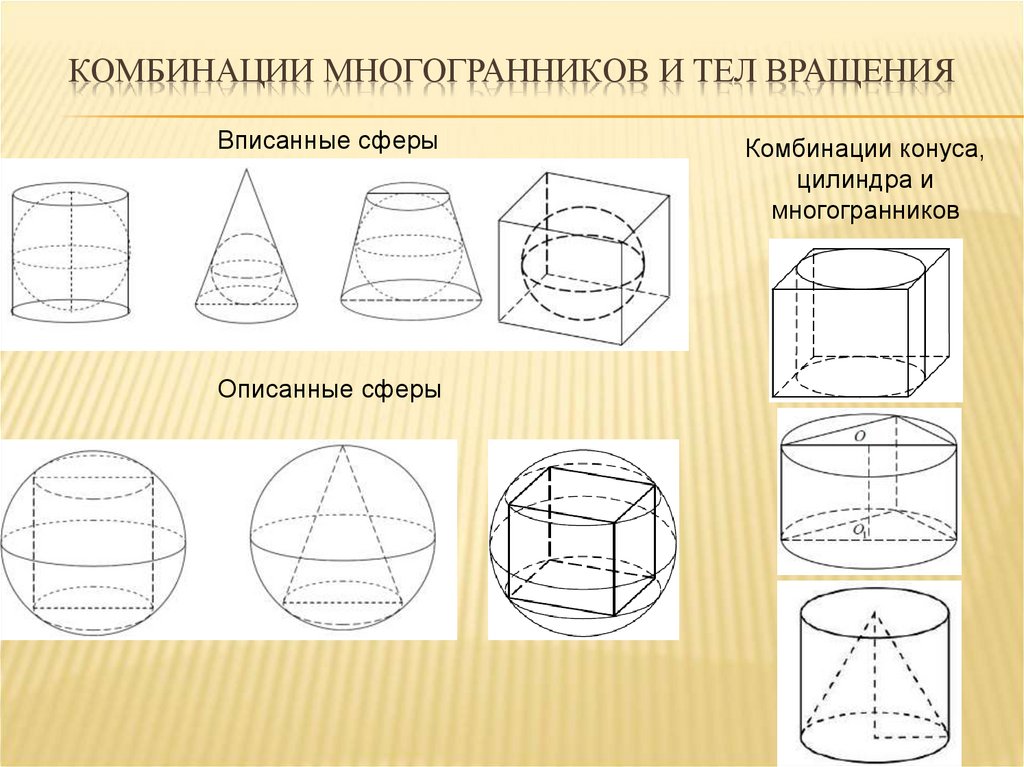
32. Комбинации многогранников и тел вращения

КОМБИНАЦИИ МНОГОГРАННИКОВ И ТЕЛ ВРАЩЕНИЯ
Вписанные сферы
Описанные сферы
Комбинации конуса,
цилиндра и
многогранников

33.

Шар вписан в цилиндр. Площадь полной поверхности
цилиндра равна 18. Найдите площадь поверхности шара
Решение.
Радиусы шара и основания цилиндра равны.
Площадь поверхности цилиндра, с радиусом
основания r и высотой 2r равна
Площадь поверхности шара радиуса r равна
,
то есть в 1,5 раза меньше площади поверхности цилиндра.
Следовательно, площадь поверхности шара равна 12.
Ответ: 12.

34.

СПАСИБО ЗА ВНИМАНИЕ!