Похожие презентации:
Решение заданий №8. Пирамида. По материалам открытого банка задач ЕГЭ
1. Решение заданий №8 Пирамида по материалам открытого банка задач ЕГЭ по математике 2016 года http://mathege.ru/or/ege/main
МБОУ СОШ №5 – «Школа здоровья и развития» г. РадужныйРешение заданий №8
Пирамида
по материалам открытого банка
задач ЕГЭ по математике 2016 года
http://mathege.ru/or/ege/main
Учитель математики: Семёнова Елена Юрьевна
2.
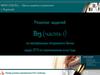
№1Стороны основания правильной четырехугольной пирамиды
равны 100, боковые ребра равны 130. Найдите площадь боковой
поверхности этой пирамиды.
Решение.
В правильной пирамиде боковые
грани равнобедренные треугольники .
S
SH высота и медиана одного из них .
В п / у SHC по т. Пифагора
130
SH 2 130 2 50 2 120 2
h
С
50
Н
D
O
A
100
SH 2 SC 2 HC 2
B
SH 120
1
Pосн . SН
2
Pосн . 4 АВ 4 100 400
S бок.
S бок.
1
400 120 24000.
2
Ответ: 24000.
3.
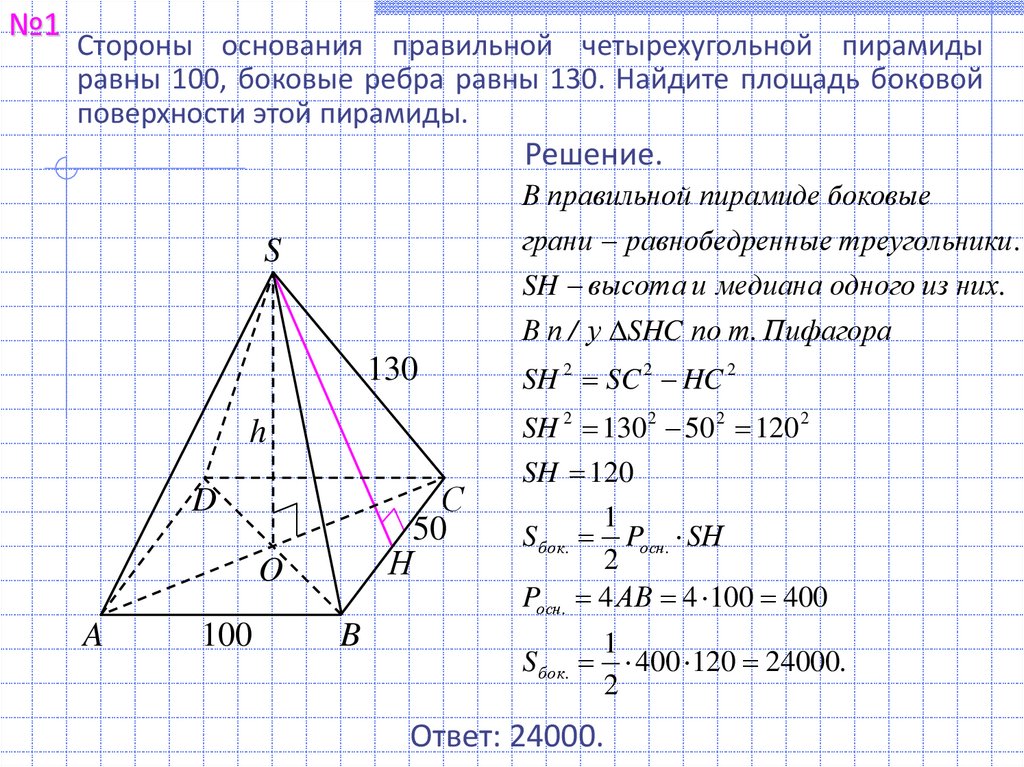
№2Стороны основания правильной шестиугольной пирамиды равны
100, боковые ребра равны 130. Найдите площадь боковой
поверхности этой пирамиды.
Решение.
S
В правильной пирамиде боковые
грани равнобедренные треугольники .
SH высота и медиана одного из них .
В п / у SHC по т. Пифагора
130
SH 2 130 2 50 2 120 2
M
SH 120
D
E
F
C
50
Н
O
A
SH 2 SC 2 HC 2
100
B
1
Pосн . SН
2
Pосн . 6 АВ 6 100 600
S бок.
S бок.
1
600 120 36000.
2
Ответ: 36000.
4.
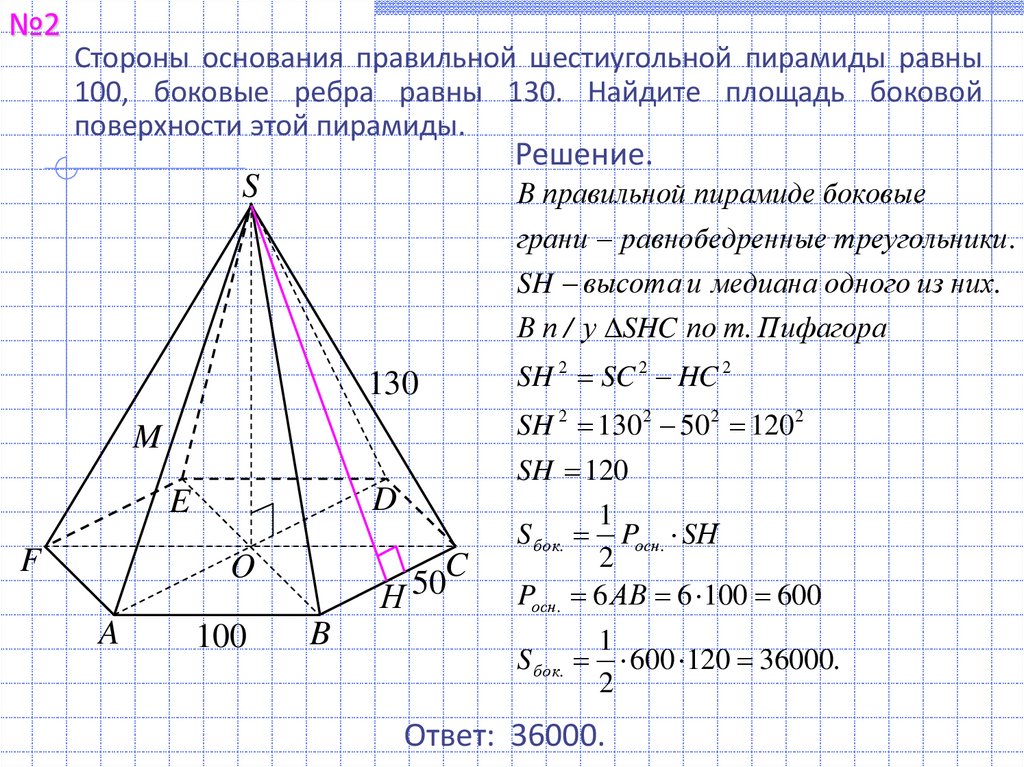
№3Во сколько раз увеличится объём правильного тетраэдра, если все
его ребра увеличить в десять раз?
Решение.
S
Объемы подобных тел относятся
как куб коэффицент а подобия
a
V2
k 3 103 1000.
V1
h
А
С
O
a
В
Ответ: 1000.
5.
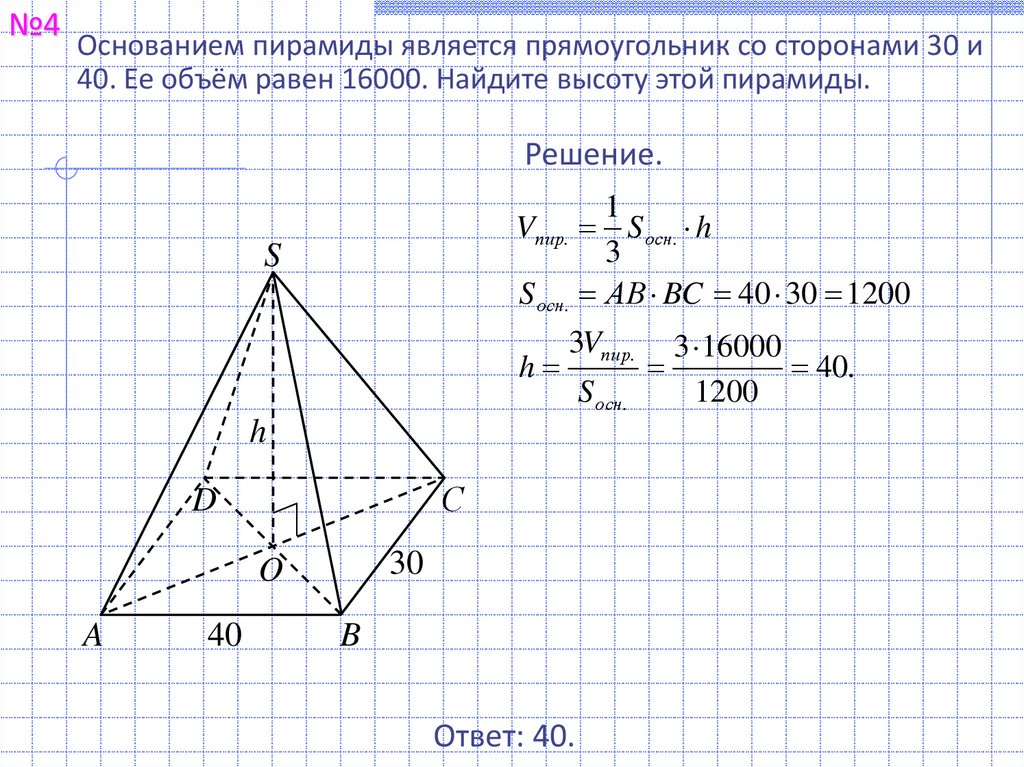
№4Основанием пирамиды является прямоугольник со сторонами 30 и
40. Ее объём равен 16000. Найдите высоту этой пирамиды.
Решение.
1
Vпир. S осн. h
3
S осн. АВ BC 40 30 1200
S
h
3Vпир.
h
С
D
30
O
A
40
B
Ответ: 40.
S осн.
3 16000
40.
1200
6.
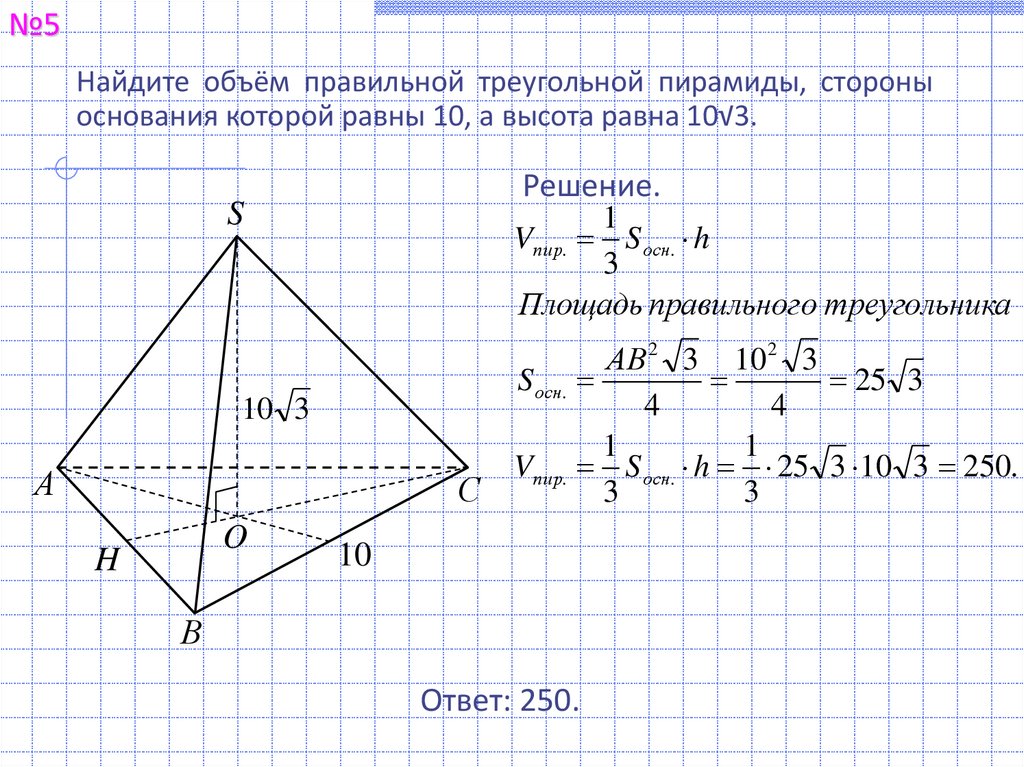
№5Найдите объём правильной треугольной пирамиды, стороны
основания которой равны 10, а высота равна 10√3.
Решение.
S
1
Vпир. S осн . h
3
Площадь правильного треугольника
10 3
А
С
O
H
АВ 2 3 10 2 3
S осн .
25 3
4
4
1
1
Vпир. S осн . h 25 3 10 3 250.
3
3
10
В
Ответ: 250.
7.
№6Найдите высоту правильной треугольной пирамиды, стороны
основания которой равны 20, а объём равен 1000√3.
Решение.
S
1
Vпир. S осн. h
3
Площадь правильного треугольника
h
А
С
O
H
АВ 2 3 20 2 3
S осн.
100 3
4
4
3Vпир. 3 1000 3
h
30.
S осн.
100 3
20
В
Ответ: 30.
8.
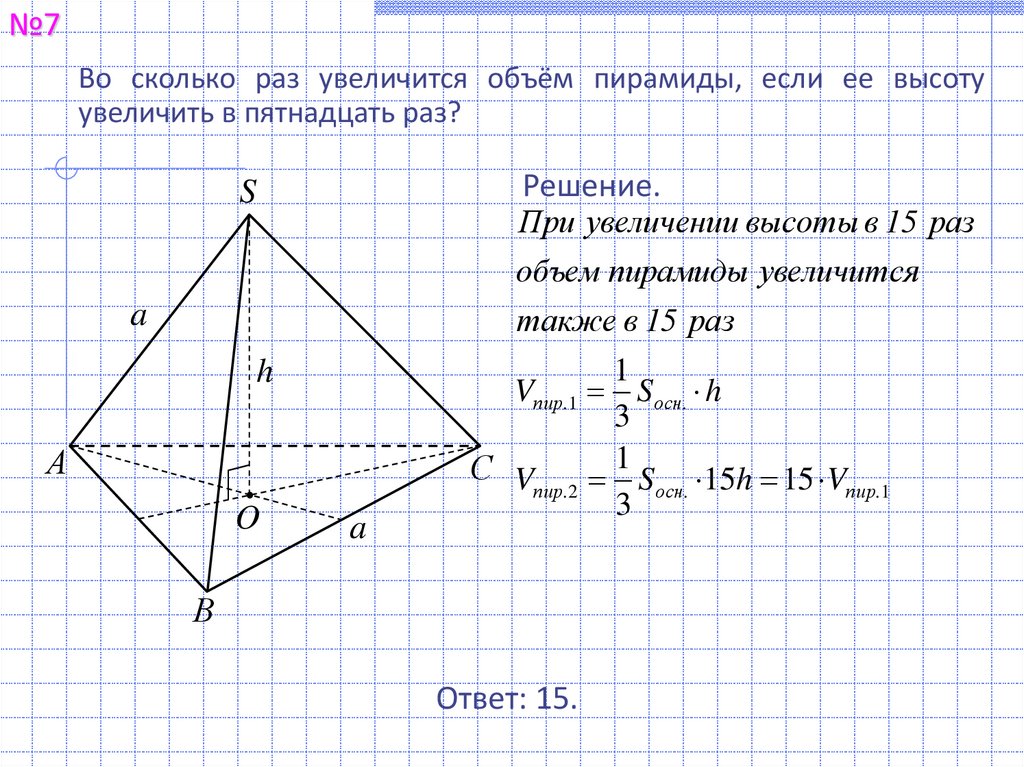
№7Во сколько раз увеличится объём пирамиды, если ее высоту
увеличить в пятнадцать раз?
S
a
h
А
O
a
Решение.
При увеличении высоты в 15 раз
объем пирамиды увеличится
также в 15 раз
1
Vпир.1 S осн. h
3
1
С V
S осн. 15h 15 Vпир.1
пир.2
3
В
Ответ: 15.
9.
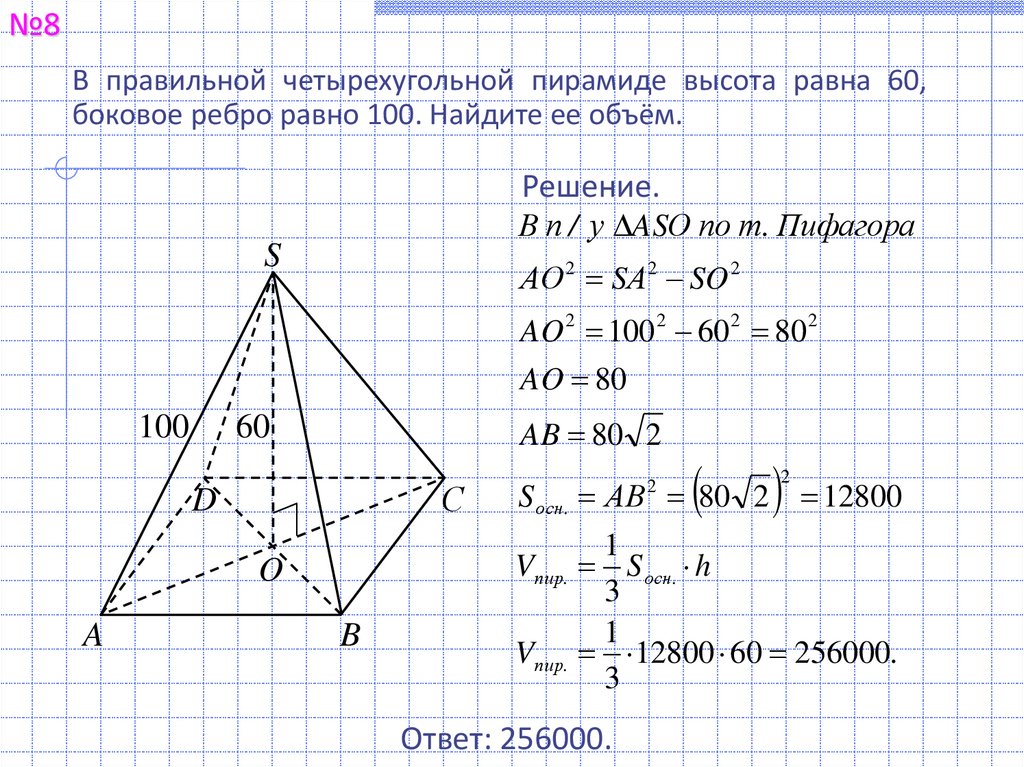
№8В правильной четырехугольной пирамиде высота равна 60,
боковое ребро равно 100. Найдите ее объём.
Решение.
В п / у ASО по т. Пифагора
S
АО 2 SА2 SO 2
AO 2 100 2 60 2 80 2
AO 80
100
AB 80 2
60
С
D
O
A
B
2
S осн . АВ 80 2 12800
2
1
Vпир. S осн . h
3
1
Vпир. 12800 60 256000.
3
Ответ: 256000.
10.
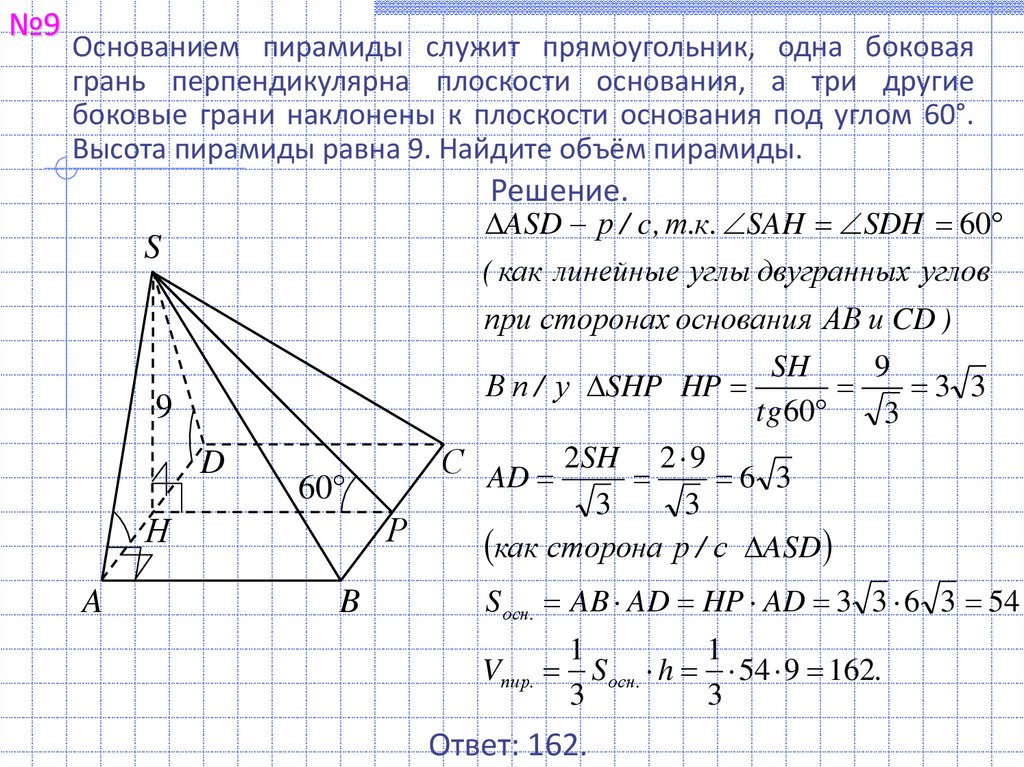
№9Основанием пирамиды служит прямоугольник, одна боковая
грань перпендикулярна плоскости основания, а три другие
боковые грани наклонены к плоскости основания под углом 60°.
Высота пирамиды равна 9. Найдите объём пирамиды.
Решение.
ASD р / c , т.к . SAH SDH 60
S
( как линейные углы двугранных углов
при сторонах основания АВ и CD )
В п / у SHP HP
9
D
A
С AD 2 SH 2 9 6 3
60°
Р
Н
B
SH
9
3 3
tg 60
3
3
3
как сторона р / с ASD
S осн . AB AD HP AD 3 3 6 3 54
1
1
Vпир. S осн . h 54 9 162.
3
3
Ответ: 162.
11.
№10Боковые ребра треугольной пирамиды взаимно перпендикулярны,
каждое из них равно 30. Найдите объём пирамиды.
S
30
А
O
С
В
S
А
В
Решение.
Повернем пирамиду на одну из
боковых граней так, что боковое
ребро станет высотой пирамиды
1
С Vпир. S осн. h
3
В п / у SAB
1
1
S осн. SB SA 30 30 450
2
2
1
Vпир.2 450 30 4500.
3
Ответ: 4500.
12.
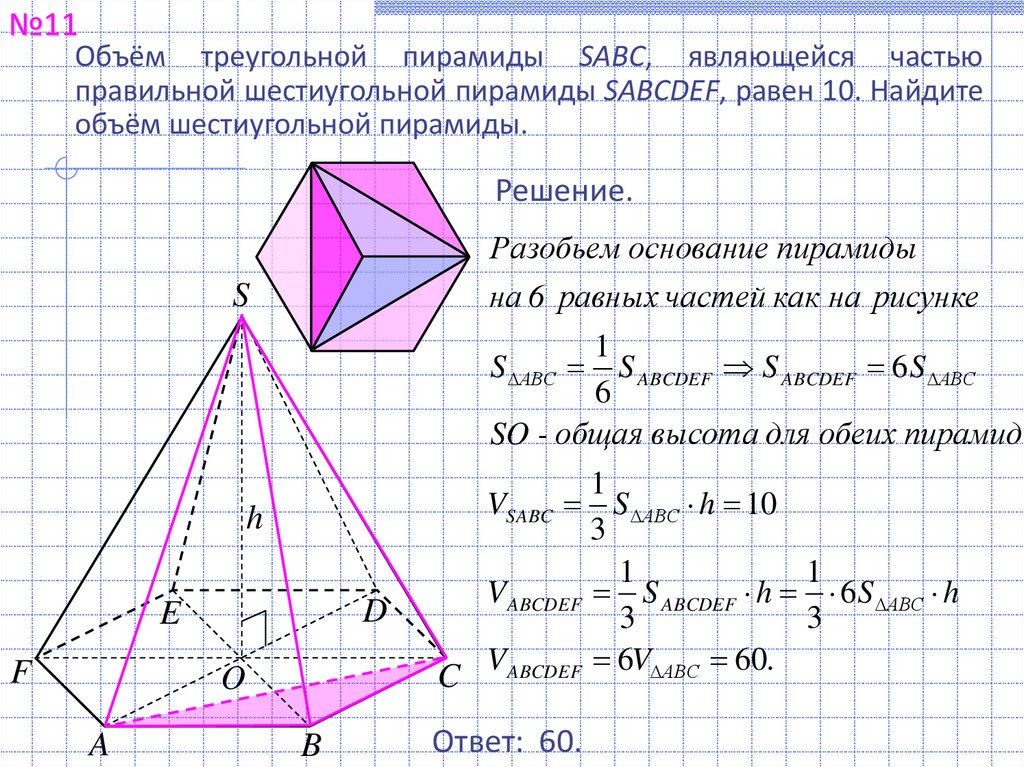
№11Объём треугольной пирамиды SABC, являющейся частью
правильной шестиугольной пирамиды SABCDEF, равен 10. Найдите
объём шестиугольной пирамиды.
Решение.
Разобьем основание пирамиды
на 6 равных частей как на рисунке
S
1
S АВС S ABCDEF S ABCDEF 6 S АВС
6
SO - общая высота для обеих пирамид
h
D
E
F
C
O
A
B
1
VSABC S АВС h 10
3
1
1
VABCDEF S ABCDEF h 6 S АВС h
3
3
VABCDEF 6V АВС 60.
Ответ: 60.
13.
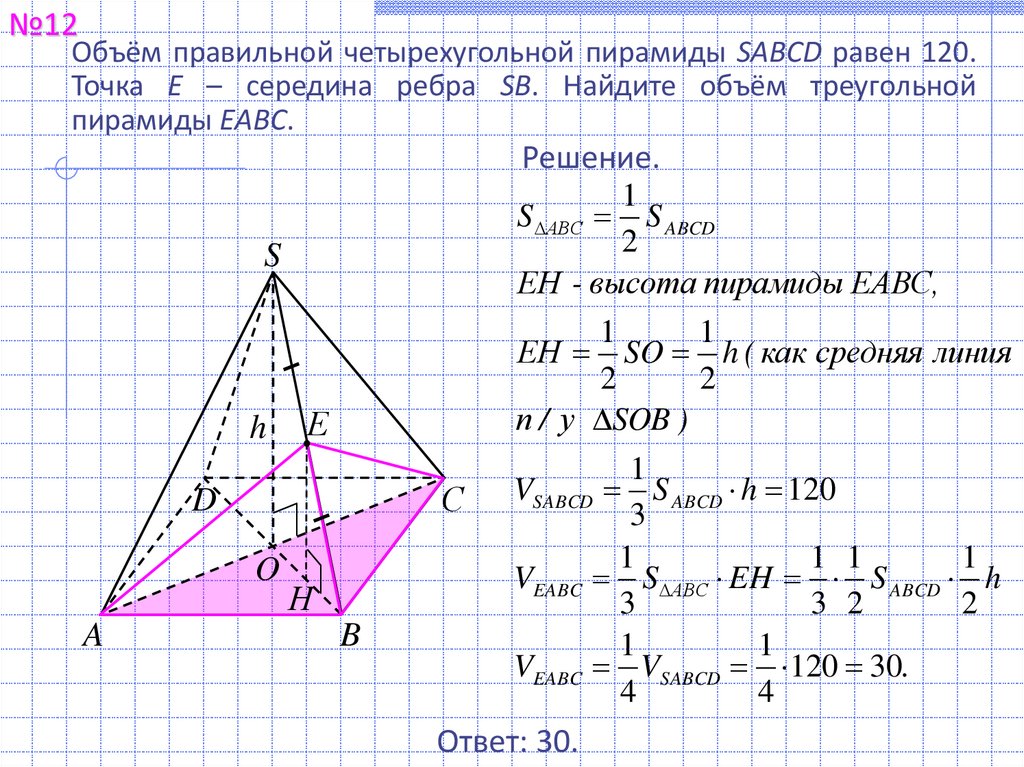
№12Объём правильной четырехугольной пирамиды SABCD равен 120.
Точка E – середина ребра SB. Найдите объём треугольной
пирамиды EABC.
S
h
Е
D
O
A
Н
B
Решение.
1
S АВС S ABCD
2
ЕН - высота пирамиды ЕАВС,
1
1
ЕН SO h ( как средняя линия
2
2
п / у SOB )
1
V
S ABCD h 120
SABCD
С
3
1
1 1
1
VEABC S АВС EH S ABCD h
3
3 2
2
1
1
VEABC VSABCD 120 30.
4
4
Ответ: 30.
14.
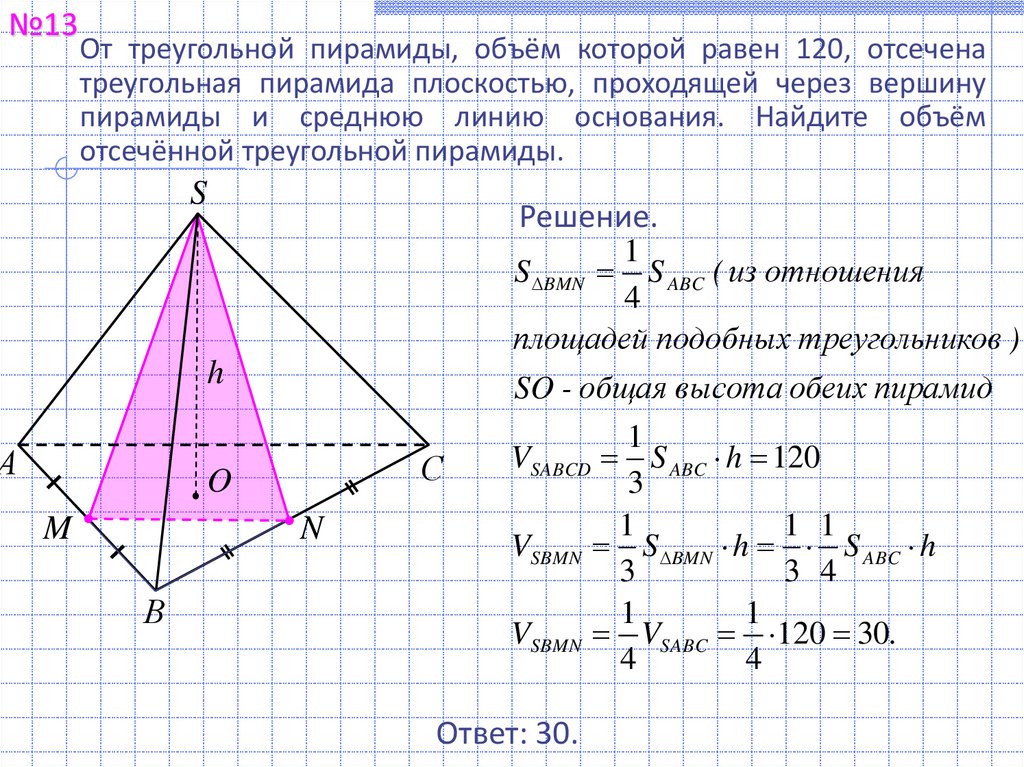
№13От треугольной пирамиды, объём которой равен 120, отсечена
треугольная пирамида плоскостью, проходящей через вершину
пирамиды и среднюю линию основания. Найдите объём
отсечённой треугольной пирамиды.
S
h
А
С
O
M
N
В
Решение.
1
S BMN S ABC ( из отношения
4
площадей подобных треугольников )
SO - общая высота обеих пирамид
1
VSABCD S ABC h 120
3
1
1 1
VSBMN S BMN h S ABC h
3
3 4
1
1
VSBMN VSABC 120 30.
4
4
Ответ: 30.
15.
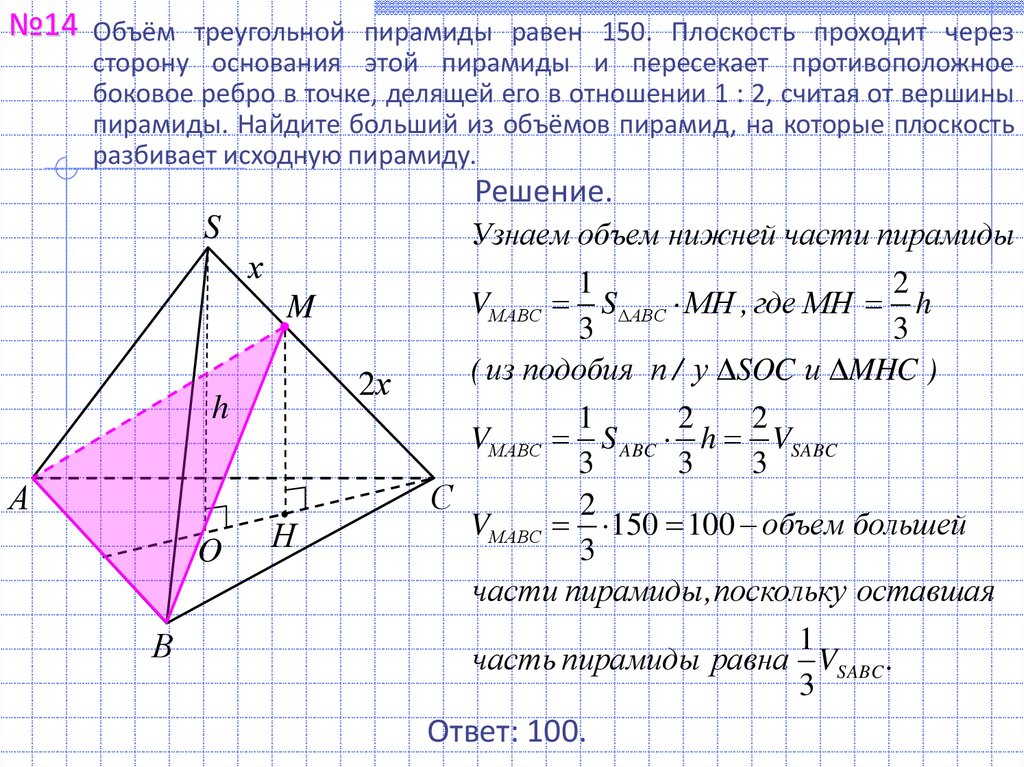
№14 Объём треугольной пирамиды равен 150. Плоскость проходит черезсторону основания этой пирамиды и пересекает противоположное
боковое ребро в точке, делящей его в отношении 1 : 2, считая от вершины
пирамиды. Найдите больший из объёмов пирамид, на которые плоскость
разбивает исходную пирамиду.
Решение.
S
Узнаем объем нижней части пирамиды
х
M
2х
h
А
O
В
Н
1
2
VМABC S АВС МH , где МН h
3
3
( из подобия п / у SOC и MHC )
1
2
2
VМABC S ABC h VSABC
3
3
3
С
2
VМABC 150 100 объем большей
3
части пирамиды , поскольку оставшая
1
часть пирамиды равна VSABC .
3
Ответ: 100.
16.
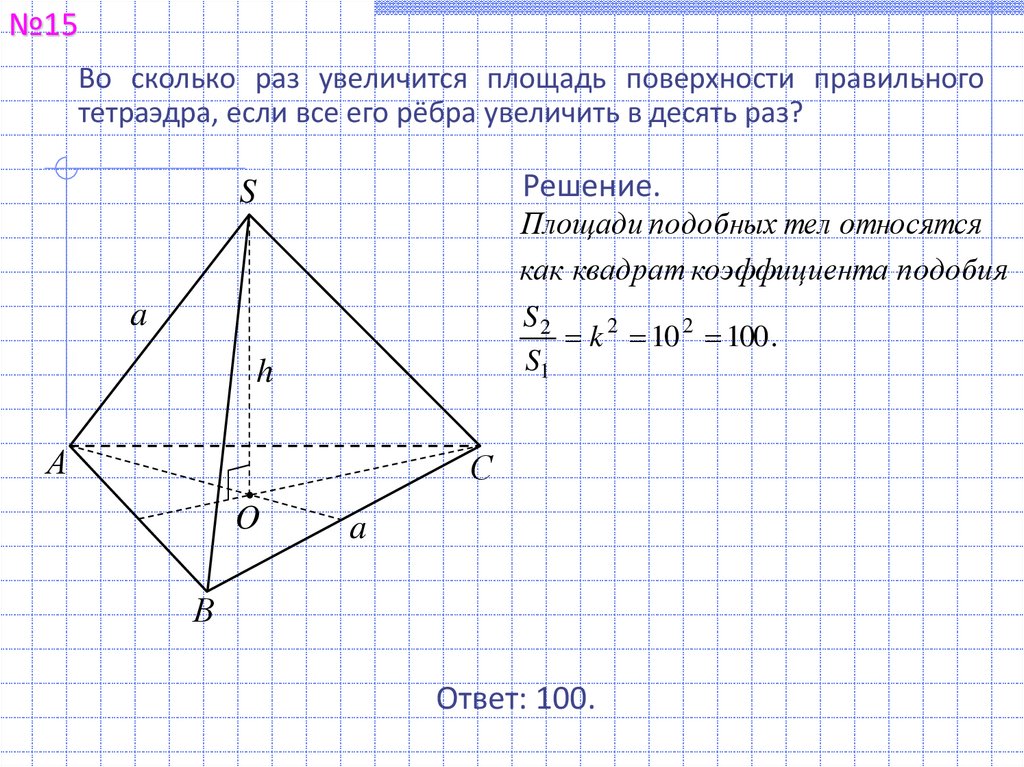
№15Во сколько раз увеличится площадь поверхности правильного
тетраэдра, если все его рёбра увеличить в десять раз?
Решение.
S
Площади подобных тел относятся
как квадрат коэффициента подобия
a
S2
k 2 10 2 100 .
S1
h
А
С
O
a
В
Ответ: 100.
17.
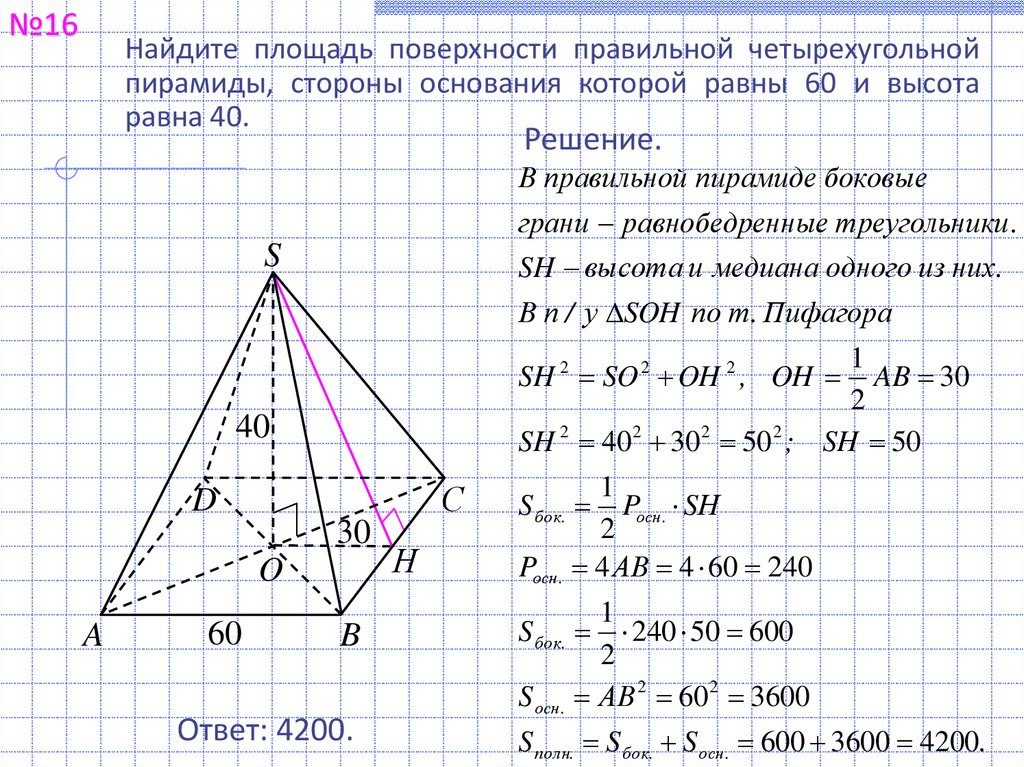
№16Найдите площадь поверхности правильной четырехугольной
пирамиды, стороны основания которой равны 60 и высота
равна 40.
Решение.
В правильной пирамиде боковые
грани равнобедренные треугольники .
S
SH высота и медиана одного из них.
В п / у SOH по т. Пифагора
1
AB 30
2
SH 2 40 2 30 2 50 2 ; SH 50
SH 2 SO 2 OH 2 , OH
40
С
D
30
O
A
60
B
Ответ: 4200.
Н
1
Pосн. SН
2
Pосн. 4 АВ 4 60 240
S бок.
1
240 50 600
2
S осн. АВ 2 60 2 3600
S бок.
S полн. S бок. S осн. 600 3600 4200.
18.
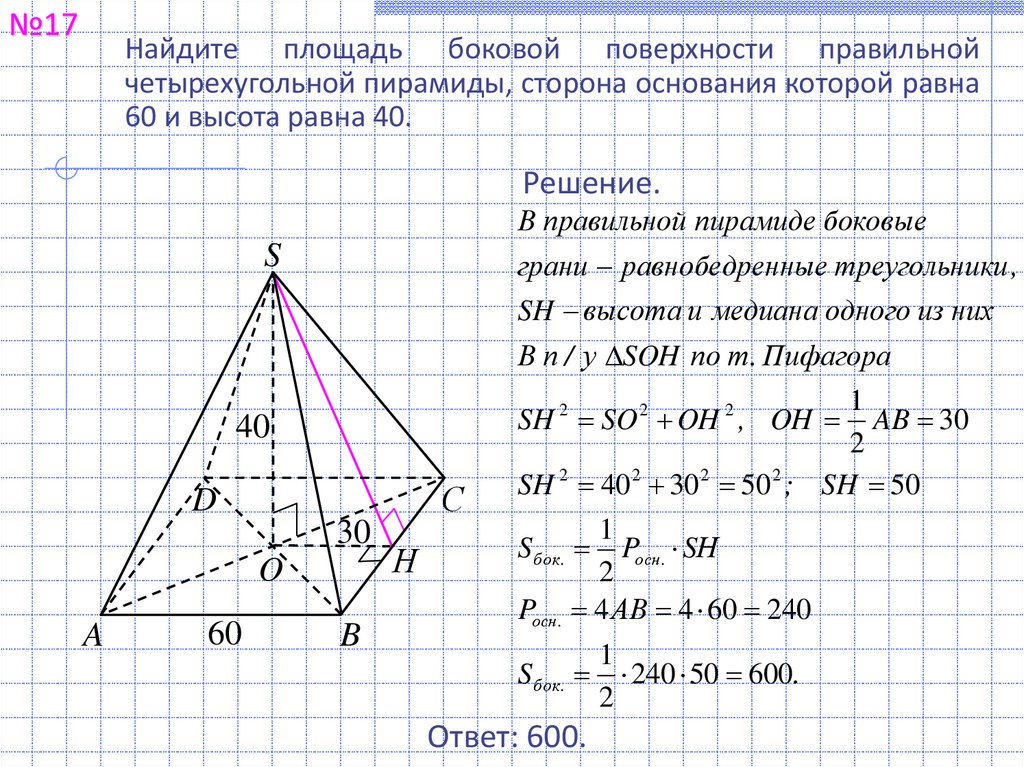
№17Найдите площадь боковой поверхности правильной
четырехугольной пирамиды, сторона основания которой равна
60 и высота равна 40.
Решение.
В правильной пирамиде боковые
S
грани равнобедренные треугольники ,
SH высота и медиана одного из них
В п / у SOH по т. Пифагора
40
С
D
30
O
A
60
1
AB 30
2
SH 2 40 2 30 2 50 2 ; SH 50
SH 2 SO 2 OH 2 , OH
B
Н
1
Pосн . SН
2
Pосн . 4 АВ 4 60 240
S бок.
S бок.
Ответ: 600.
1
240 50 600.
2
19.
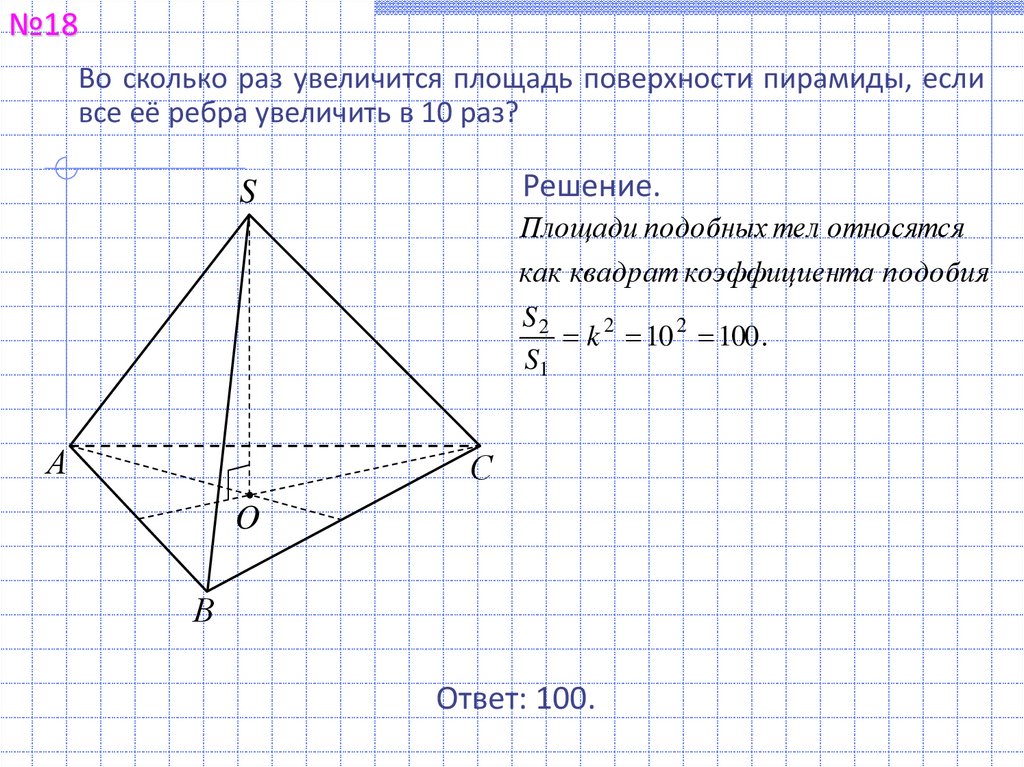
№18Во сколько раз увеличится площадь поверхности пирамиды, если
все её ребра увеличить в 10 раз?
Решение.
S
Площади подобных тел относятся
как квадрат коэффициента подобия
S2
k 2 10 2 100 .
S1
А
С
O
В
Ответ: 100.
20.
№19Ребра тетраэдра равны 10. Найдите площадь
проходящего через середины четырех его ребер.
S
Q
P
А
O
M
N
сечения,
Решение.
Стороны сечения средние линии
равносторонних треугольников
( граней ), противолежащие ребра
взаимнопер пендикуляр ны, значит ,
сечение квадрат, со стороной,
С равной половине ребра
S MNPQ MN 2 52 25.
В
Ответ: 25.
21.
№20Найдите объём пирамиды, высота которой равна 60, а
основание – прямоугольник со сторонами 30 и 40.
Решение.
S
S осн . АВ BC 40 30 1200
1
1
Vпир. S осн . h 1200 60 2400.
3
3
60
С
D
30
O
A
40
B
Ответ: 2400.
22.
№21В правильной четырехугольной пирамиде высота равна 120,
объём равен 20000. Найдите боковое ребро этой пирамиды.
S
120
D
O
A
1
3V
Решение. Vпир. S осн. h S осн.
3
h
3 20000
S осн .
500
120
S осн . a 2 500 a 500 10 5
1
АО
АС , где АС а 2 ,
С
2
а 2 10 5 2
АО
5 10
2
2
B
В п / у ASO по т. Пифагора
AS 2 AO 2 OS 2
Ответ: 130.
2
AS 5 10 120 2 130 2
2
AS 130.
23.
№22Сторона основания правильной шестиугольной пирамиды равна 20,
боковое ребро равно 40. Найдите объём пирамиды.
Решение.
S
В правильном шестиугольнике
ОС АВ 20 ,
3а 2 3 3 20 2 3
S осн .
600 3
2
2
В п / у SOC по т. Пифагора
40
SO 2 SC 2 OC 2
SO 2 40 2 20 2 1200
D
E
F
C
O
A
20
SO 20 3
B
1
Vпир. S осн . h
3
1
Vпир. 600 3 20 3 12000.
3
Ответ: 12000.
24.
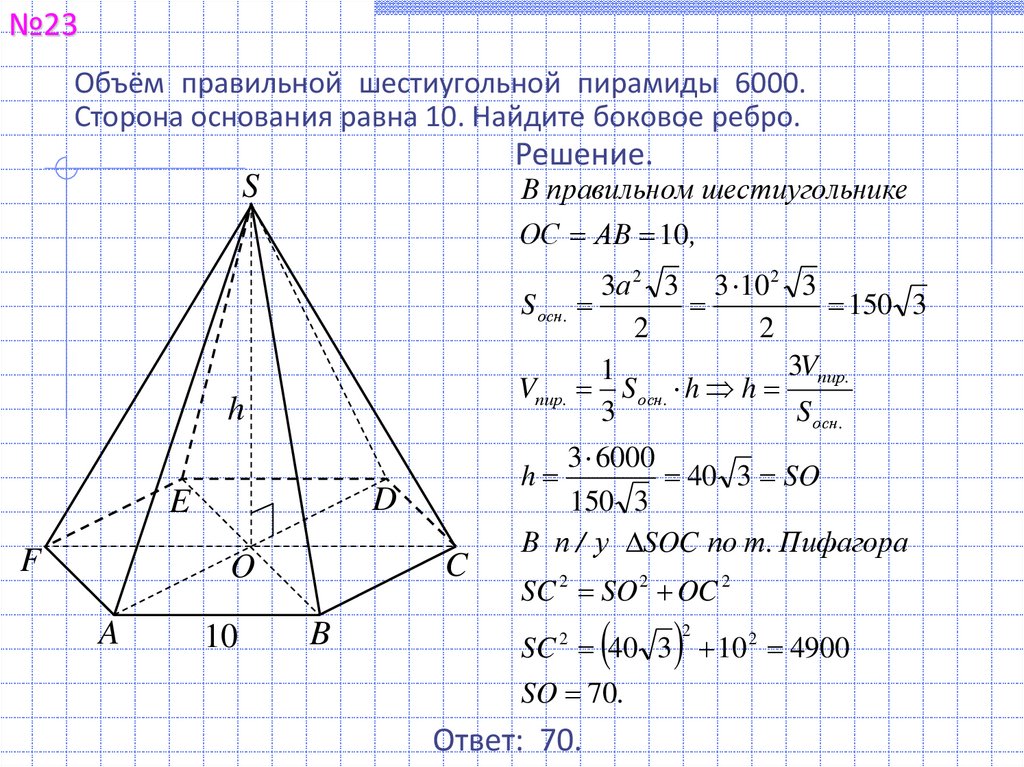
№23Объём правильной шестиугольной пирамиды 6000.
Сторона основания равна 10. Найдите боковое ребро.
Решение.
В правильном шестиугольнике
S
ОС АВ 10 ,
3а 2 3 3 10 2 3
S осн.
150 3
2
2
3Vпир.
1
Vпир. S осн. h h
3
S осн.
h
D
E
F
C
O
A
10
B
3 6000
40 3 SO
150 3
В п / у SOC по т. Пифагора
h
SC 2 SO 2 OC 2
2
SC 40 3 10 2 4900
2
SO 70.
Ответ: 70.
25.
№24Сторона основания правильной шестиугольной пирамиды равна
40, а угол между боковой гранью и основанием равен 45°.
Найдите объём пирамиды.
Решение.
S
В правильном шестиугольнике
а 3 40 3
OH
20 3
2
2
3а 2 3 3 40 2 3
S осн.
2400 3
2
2
SOH п / у , р / б
h
E
D
SO OH 20 3
Н
1
Vпир. S осн. h
3
1
Vпир. 2400 3 20 3 4800.
3
45°
F
O
A
40
B
C
Ответ: 4800.
26.
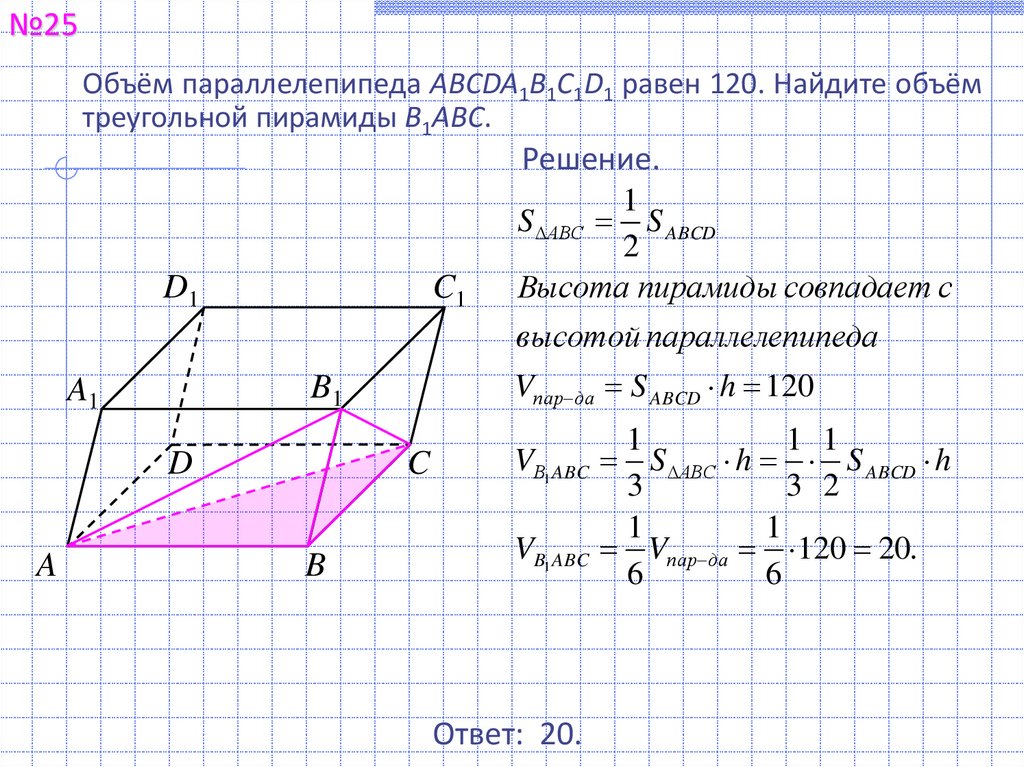
№25Объём параллелепипеда ABCDA1B1C1D1 равен 120. Найдите объём
треугольной пирамиды B1ABC.
B1
Решение.
1
S АВС S ABCD
2
Высота пирамиды совпадает с
высотой параллелепипеда
Vпар да S ABCD h 120
B
1
1 1
VВ1 ABC S АВС h S ABCD h
3
3 2
1
1
VB1 ABC Vпар да 120 20.
6
6
D1
A1
C1
D
A
C
Ответ: 20.
27.
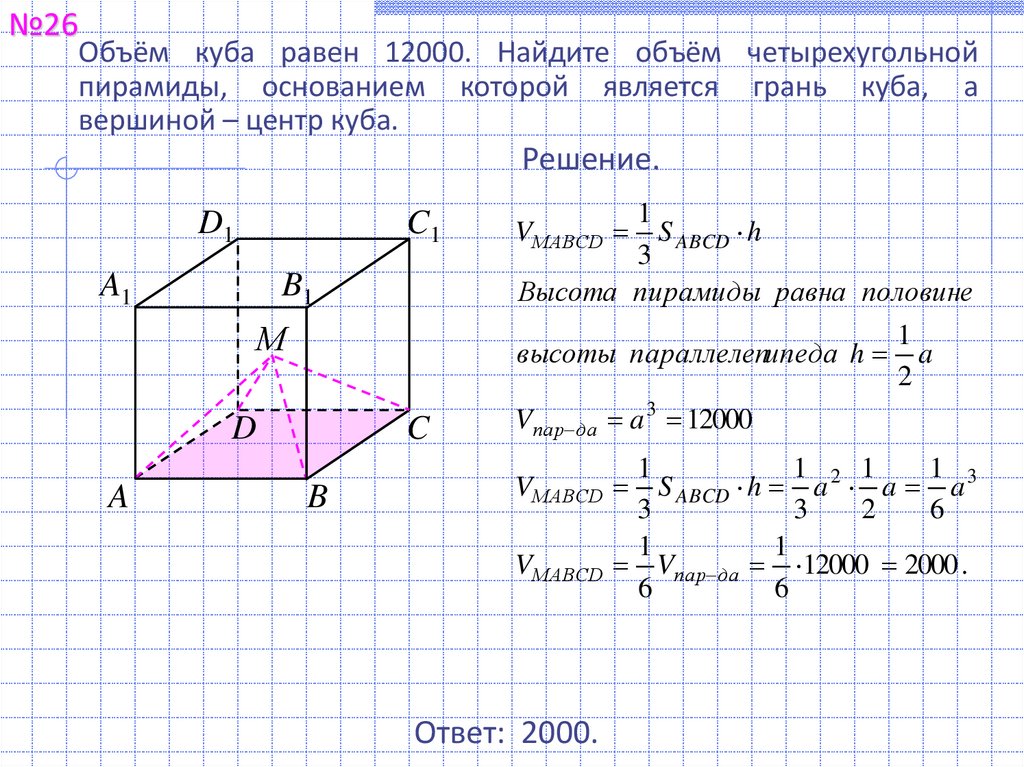
№26Объём куба равен 12000. Найдите объём четырехугольной
пирамиды, основанием которой является грань куба, а
вершиной – центр куба.
Решение.
D1
A1
C1
B1
М
высоты параллелепипеда h
D
A
1
S ABCD h
3
Высота пирамиды равна половине
VМАВСD
C
B
1
a
2
Vпар да a 3 12000
VМАВСD
VМАВСD
Ответ: 2000.
1
1 2 1
1 3
S ABCD h a a a
3
3
2
6
1
1
Vпар да 12000 2000 .
6
6
28.
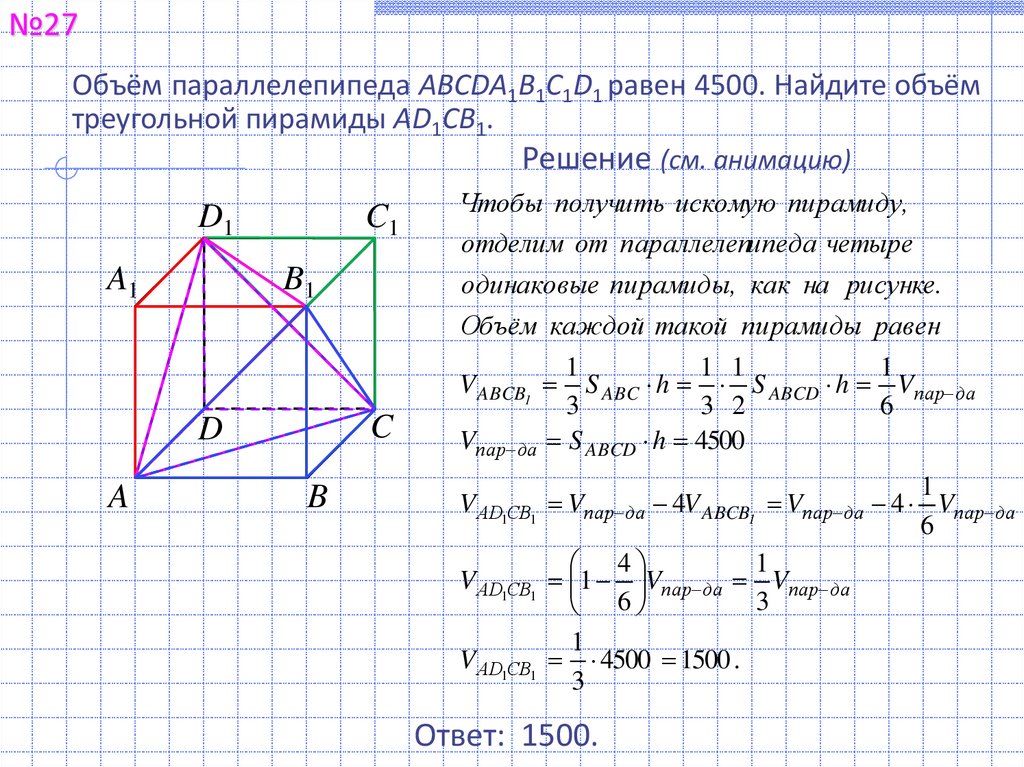
№27Объём параллелепипеда ABCDA1B1C1D1 равен 4500. Найдите объём
треугольной пирамиды AD1CB1.
Решение (см. анимацию)
D1
A1
C1
B1
Чтобы получить искомую пирамиду,
отделим от параллелепипеда четыре
одинаковые пирамиды, как на рисунке.
Объём каждой такой пирамиды равен
1
1 1
1
S ABC h S ABCD h Vпар да
3
3 2
6
S ABCD h 4500
V ABCB1
C
D
A
B
Vпар да
V АD1СВ1
V АD1СВ1
V АD1СВ1
1
Vпар да 4V ABCB1 Vпар да 4 Vпар да
6
1
4
1 Vпар да Vпар да
3
6
1
4500 1500 .
3
Ответ: 1500.
29.
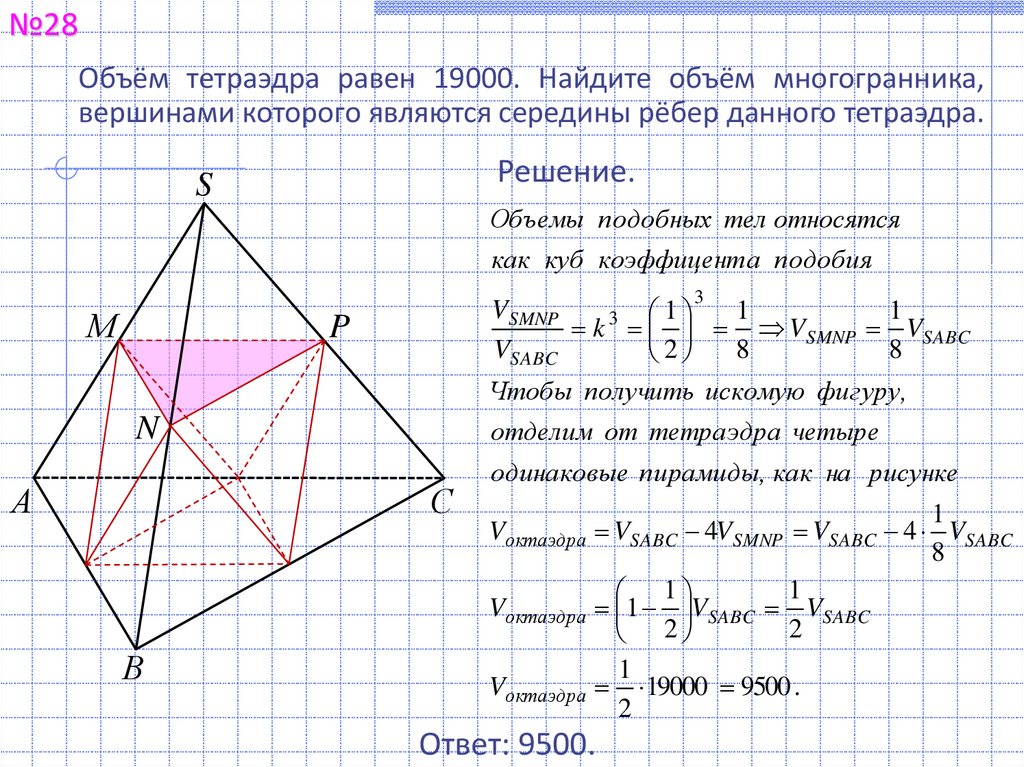
№28Объём тетраэдра равен 19000. Найдите объём многогранника,
вершинами которого являются середины рёбер данного тетраэдра.
Решение.
S
Объемы подобных тел относятся
как куб коэффицент а подобия
3
М
VSMNP
1
1
1
k 3 VSMNP VSABC
VSABC
8
8
2
Чтобы получить искомую фигуру,
P
N
А
отделим от тетраэдра четыре
С
В
одинаковые пирамиды, как на рисунке
1
Vоктаэдра VSABC 4VSMNP VSABC 4 VSABC
8
1
1
Vоктаэдра 1 VSABC VSABC
2
2
1
Vоктаэдра 19000 9500 .
2
Ответ: 9500.
30.
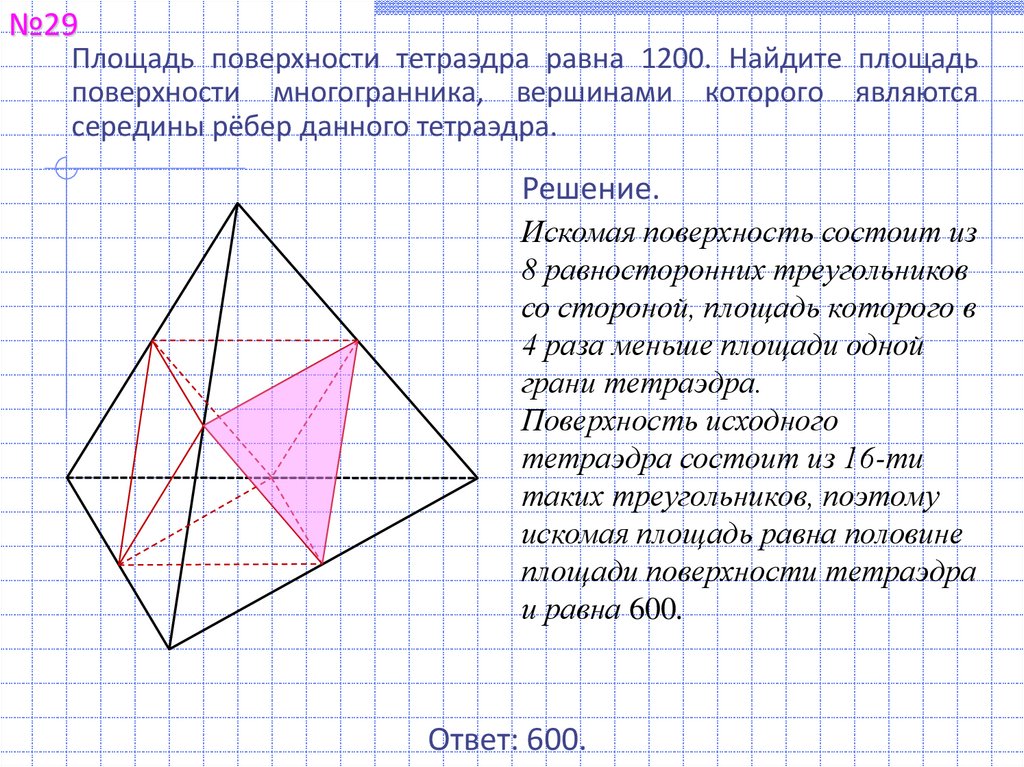
№29Площадь поверхности тетраэдра равна 1200. Найдите площадь
поверхности многогранника, вершинами которого являются
середины рёбер данного тетраэдра.
Решение.
Искомая поверхность состоит из
8 равносторонних треугольников
со стороной, площадь которого в
4 раза меньше площади одной
грани тетраэдра.
Поверхность исходного
тетраэдра состоит из 16-ти
таких треугольников, поэтому
искомая площадь равна половине
площади поверхности тетраэдра
и равна 600.
Ответ: 600.
31.
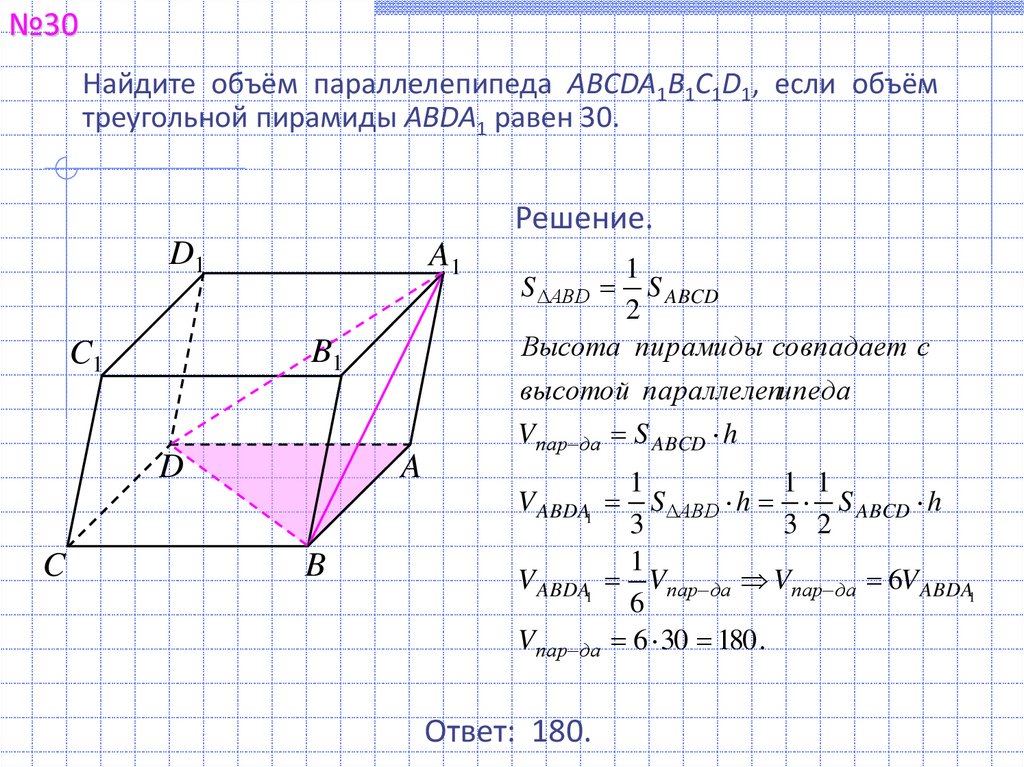
№30Найдите объём параллелепипеда ABCDA1B1C1D1, если объём
треугольной пирамиды ABDA1 равен 30.
Решение.
D1
A1
B1
C1
C
высотой параллелепипеда
A
D
B
1
S АВD S ABCD
2
Высота пирамиды совпадает с
Vпар да S ABCD h
1
1 1
S АВD h S ABCD h
3
3 2
1
V ABDA1 Vпар да Vпар да 6V ABDA1
6
Vпар да 6 30 180 .
V ABDA1
Ответ: 180.
32.
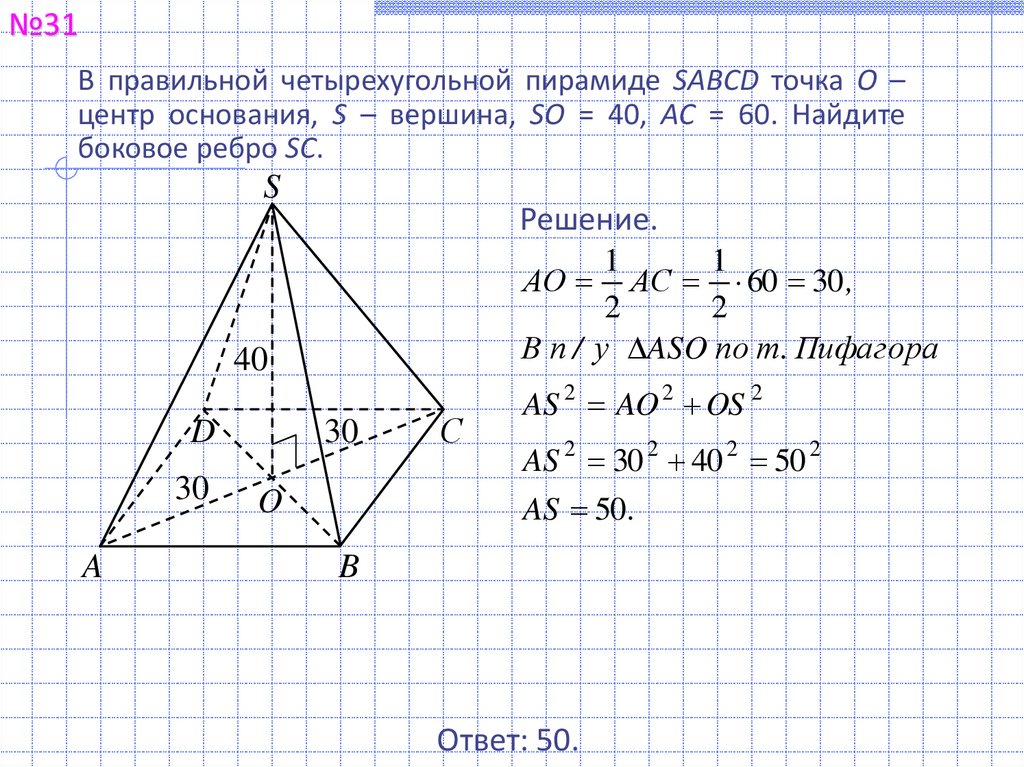
№31В правильной четырехугольной пирамиде SABCD точка О –
центр основания, S – вершина, SO = 40, AC = 60. Найдите
боковое ребро SC.
S
Решение.
1
1
АО АС 60 30 ,
2
2
В п / у ASO по т. Пифагора
40
D
30
A
30
С
AS 2 AO 2 OS 2
AS 2 30 2 40 2 50 2
AS 50 .
O
B
Ответ: 50.
33.
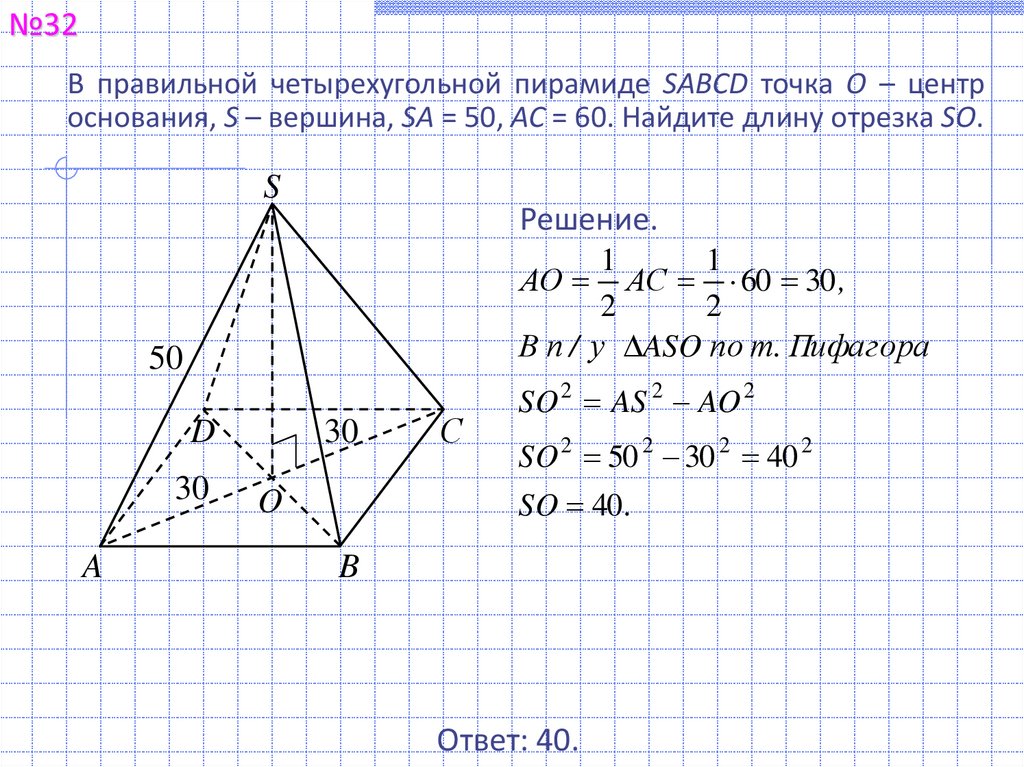
№32В правильной четырехугольной пирамиде SABCD точка О – центр
основания, S – вершина, SA = 50, AC = 60. Найдите длину отрезка SO.
S
Решение.
1
1
АО АС 60 30 ,
2
2
В п / у ASO по т. Пифагора
50
D
30
A
30
С
SO 2 AS 2 AO 2
SO 2 50 2 30 2 40 2
SO 40 .
O
B
Ответ: 40.
34.
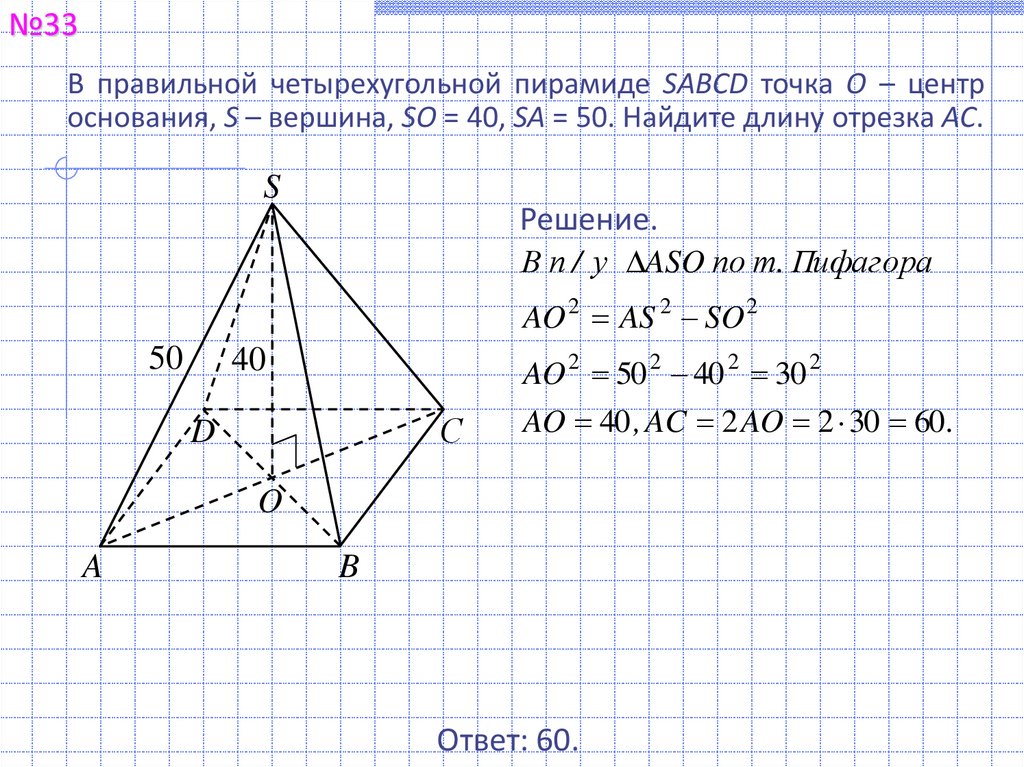
№33В правильной четырехугольной пирамиде SABCD точка О – центр
основания, S – вершина, SO = 40, SA = 50. Найдите длину отрезка AC.
S
Решение.
В п / у ASO по т. Пифагора
AO 2 AS 2 SO 2
50
40
AO 2 50 2 40 2 30 2
С
D
AO 40 , AC 2 AO 2 30 60 .
O
A
B
Ответ: 60.
35.
№34В правильной четырёхугольной пирамиде SABCD с основанием
ABCD боковое ребро SA равно 50, сторона основания равна 30√2.
Найдите объём пирамиды.
Решение.
S
Основание пирамиды квадрат ABCD ,
в котором AO
С
D
30 2
30 2
SО 2 SА 2 AO 2
SO 2 50 2 30 2 40 2
SO 40
O
A
30
2
2
В п / у ASО по т. Пифагора
h
50
AB
B
S осн. АВ 2 30 2
2
1800
1
S осн. h
3
1
1800 40 24000 .
3
Vпир.
Vпир.
Ответ: 24000.
36.
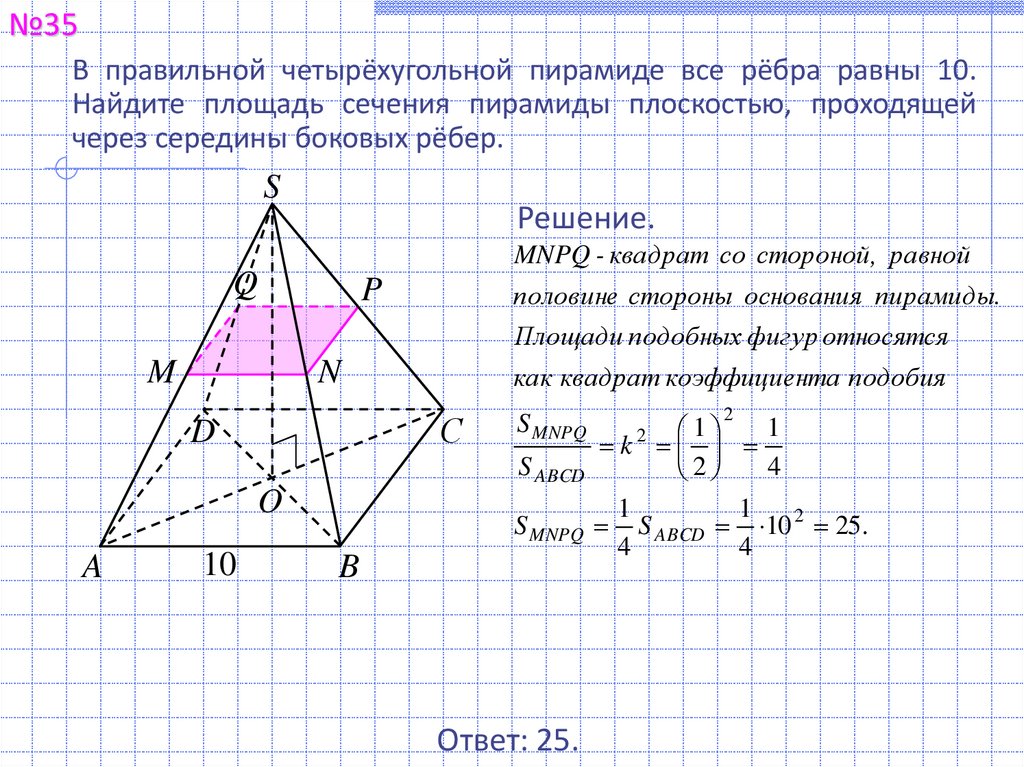
№35В правильной четырёхугольной пирамиде все рёбра равны 10.
Найдите площадь сечения пирамиды плоскостью, проходящей
через середины боковых рёбер.
S
Решение.
MNPQ - квадрат со стороной, равной
Q
P
половине стороны основания пирамиды.
Площади подобных фигур относятся
M
N
как квадрат коэффициента подобия
С
D
S MNPQ
S ABCD
O
A
10
S MNPQ
B
Ответ: 25.
2
1
1
k2
4
2
1
1
S ABCD 10 2 25 .
4
4
37.
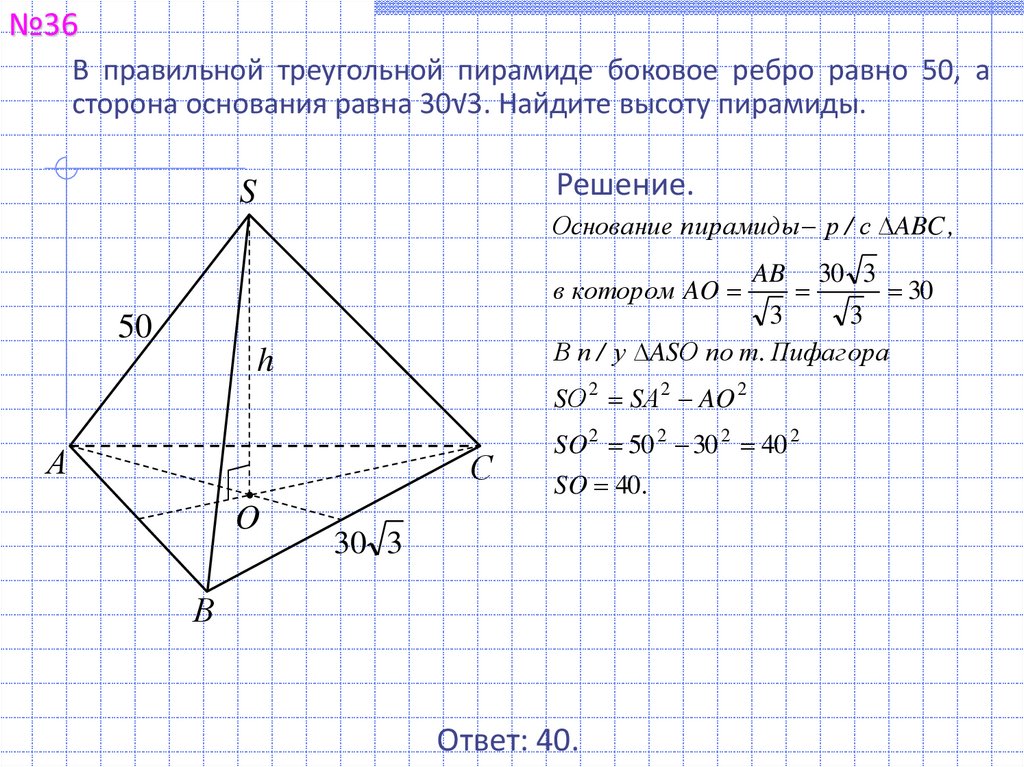
№36В правильной треугольной пирамиде боковое ребро равно 50, а
сторона основания равна 30√3. Найдите высоту пирамиды.
Решение.
S
Основание пирамиды р / с ABC ,
в котором AO
AB
30
3
3
В п / у ASО по т. Пифагора
50
h
SО 2 SА 2 AO 2
А
С
O
30 3
SO 2 50 2 30 2 40 2
SO 40 .
30 3
В
Ответ: 40.









 Математика
Математика