Стереометрия. Расстояния в пространстве. Задания В 9, ЕГЭ

1. Задания В 9 ЕГЭ - 2012.

Учитель математики МБОУ СОШ № 8
Лещенко Светлана Ивановна
Г. Туапсе
Краснодарский край

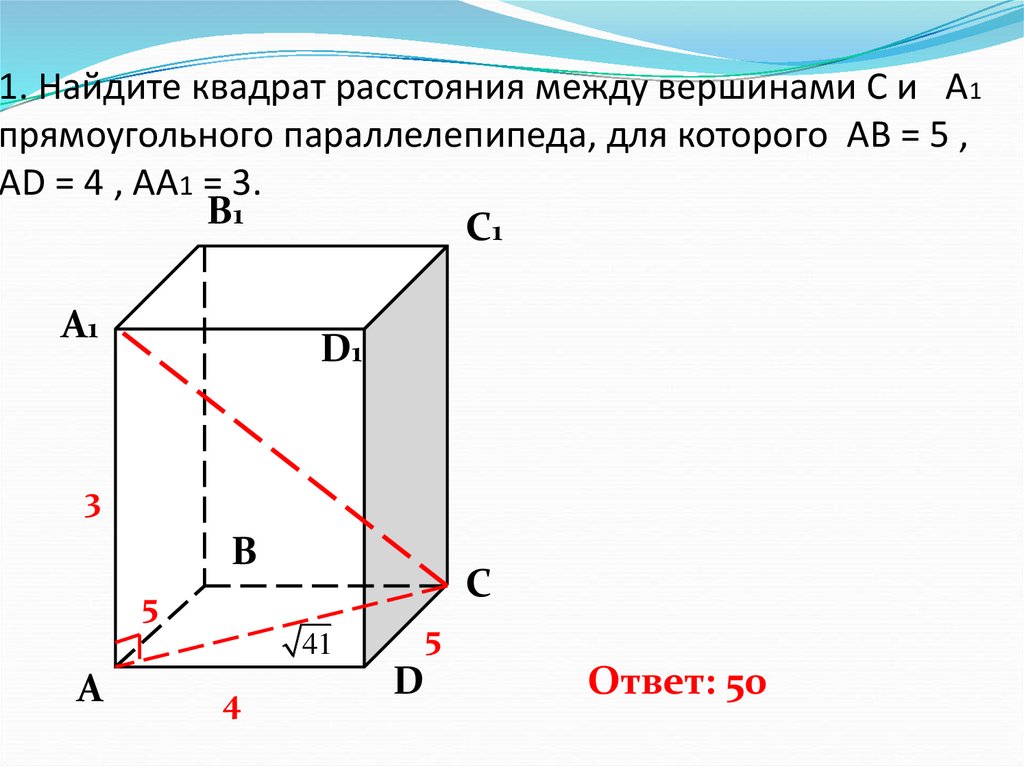
2. 1. Найдите квадрат расстояния между вершинами С и А1 прямоугольного параллелепипеда, для которого АВ = 5 , AD = 4 , AA1 = 3.

B1
C1
A1
D1
3
B
C
5
5
41
A
4
D
Ответ: 50

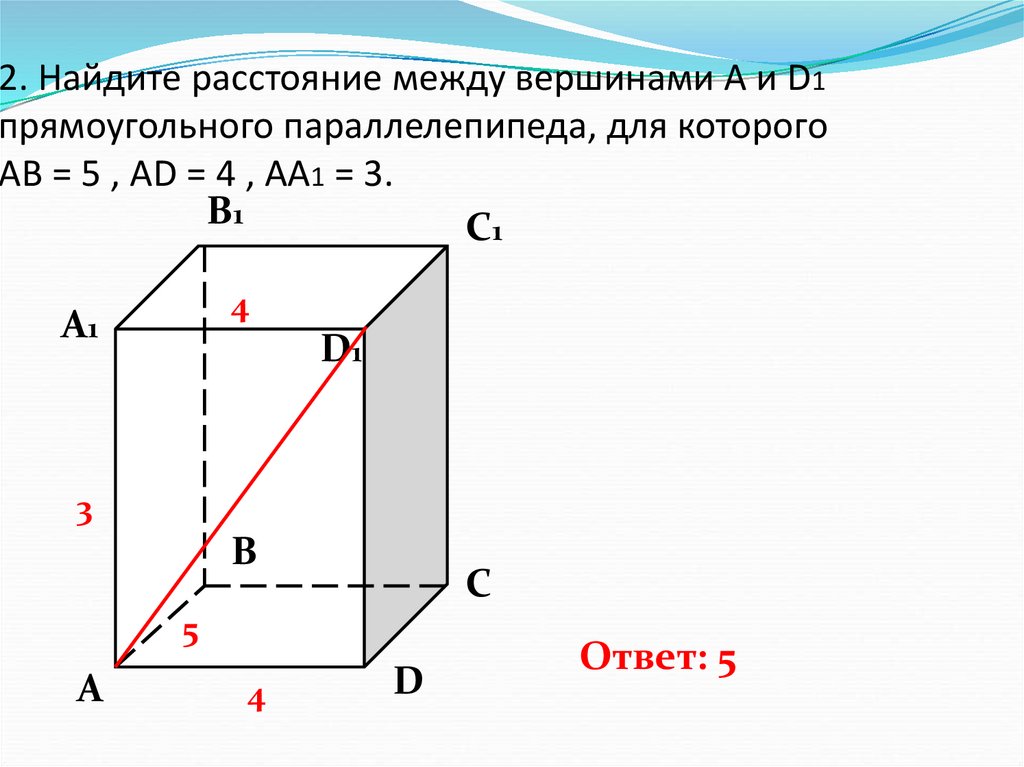
3. 2. Найдите расстояние между вершинами А и D1 прямоугольного параллелепипеда, для которого АВ = 5 , AD = 4 , AA1 = 3.

B1
C1
4
A1
D1
3
B
C
5
A
4
D
Ответ: 5

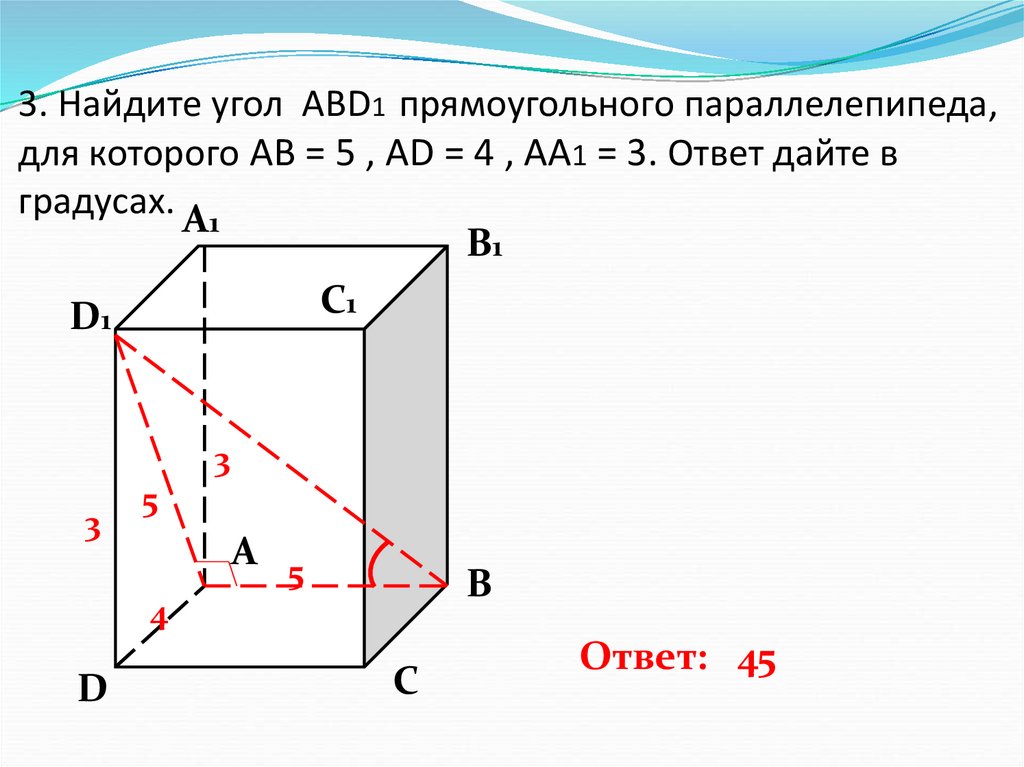
4. 3. Найдите угол ABD1 прямоугольного параллелепипеда, для которого АВ = 5 , AD = 4 , AA1 = 3. Ответ дайте в градусах.

A1
B1
C1
D1
3
3
5
A 5
B
4
D
C
Ответ: 45

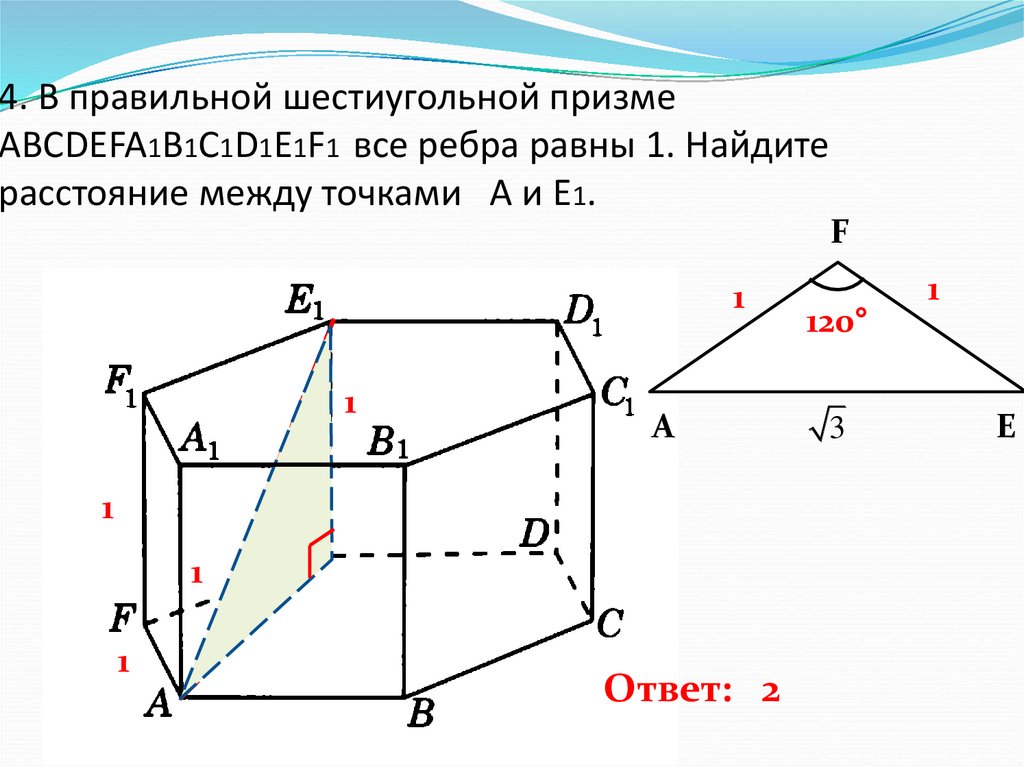
5. 4. В правильной шестиугольной призме ABCDEFA1B1C1D1E1F1 все ребра равны 1. Найдите расстояние между точками A и E1.

F
1
1
A
1
1
1
3
Ответ: 2
120°
3
1
E

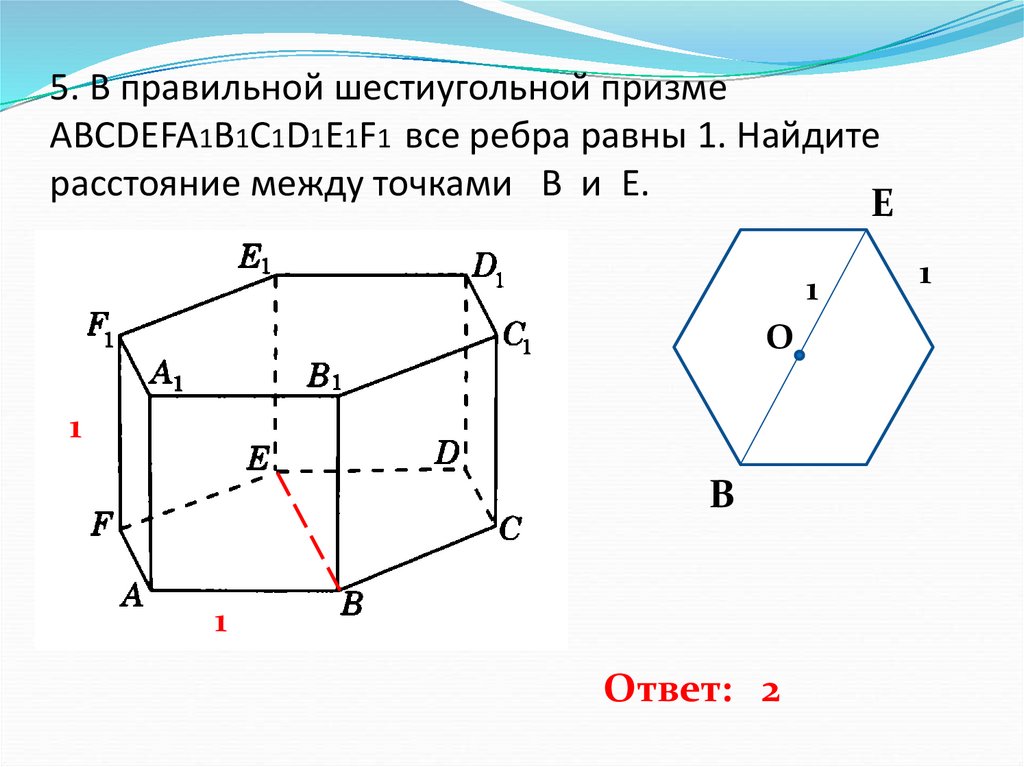
6. 5. В правильной шестиугольной призме ABCDEFA1B1C1D1E1F1 все ребра равны 1. Найдите расстояние между точками B и E.

E
1
O
1
B
1
Ответ: 2
1

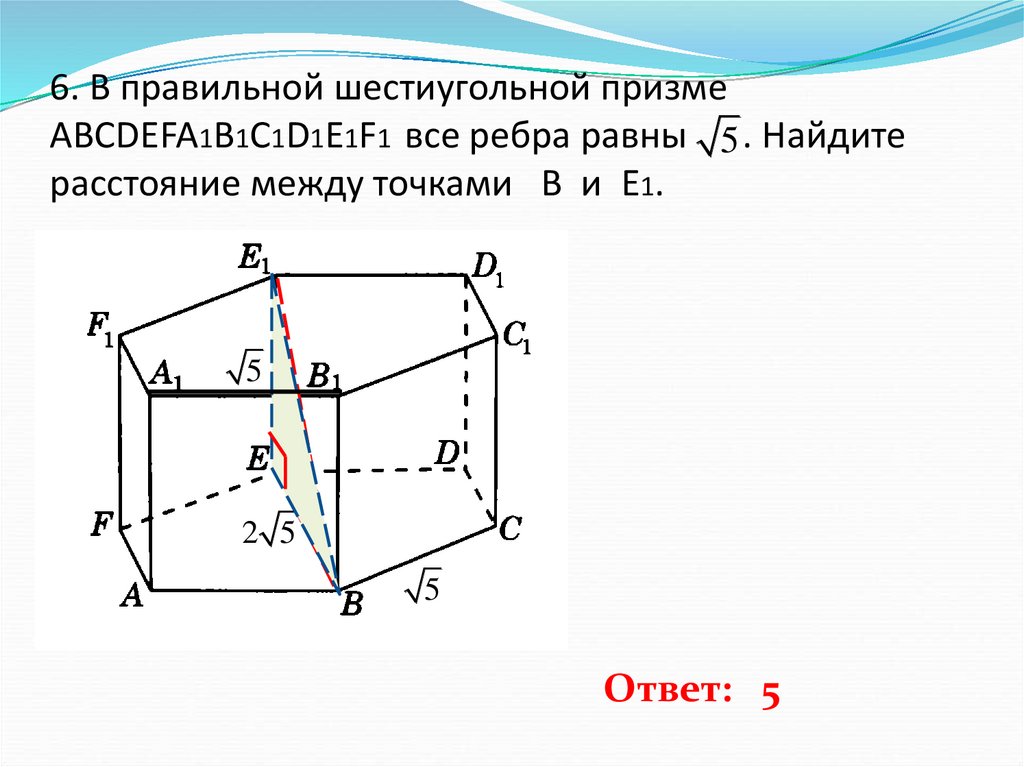
7. 6. В правильной шестиугольной призме ABCDEFA1B1C1D1E1F1 все ребра равны . Найдите расстояние между точками B и E1.

6. В правильной шестиугольной призме
ABCDEFA1B1C1D1E1F1 все ребра равны 5 . Найдите
расстояние между точками B и E1.
5
2 5
5
Ответ: 5

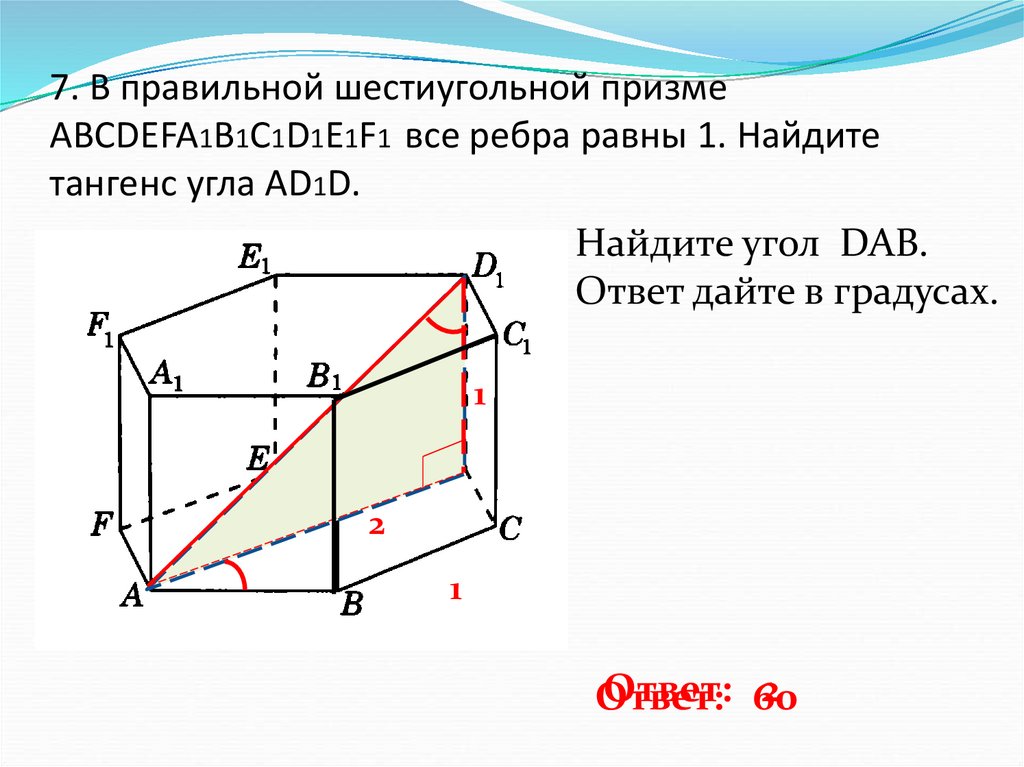
8. 7. В правильной шестиугольной призме ABCDEFA1B1C1D1E1F1 все ребра равны 1. Найдите тангенс угла AD1D.

Найдите угол DAB.
Ответ дайте в градусах.
1
2
1
Ответ: 60
2
Ответ:

9. 8. Найдите расстояние между вершинами A и C2 многогранника, изображенного на рисунке. Все двугранные углы многогранника прямые.

Найдите квадрат расстояния
между вершинами D и C2.
8
Ответ: 53

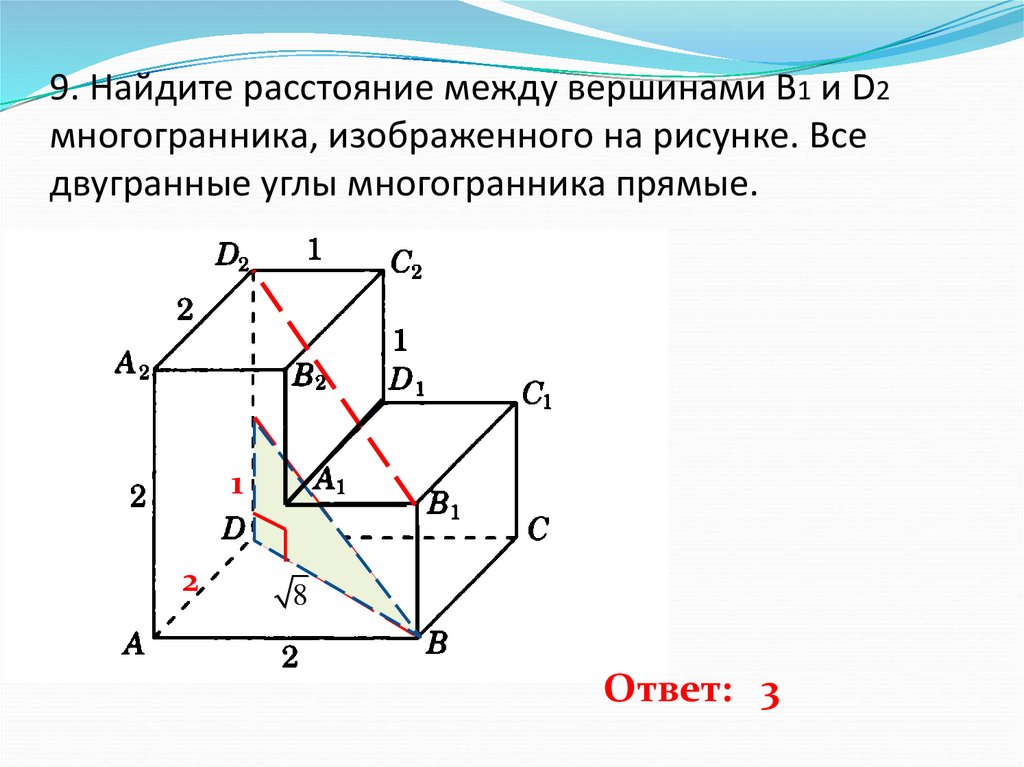
10. 9. Найдите расстояние между вершинами B1 и D2 многогранника, изображенного на рисунке. Все двугранные углы многогранника

прямые.
1
2
8
Ответ: 3

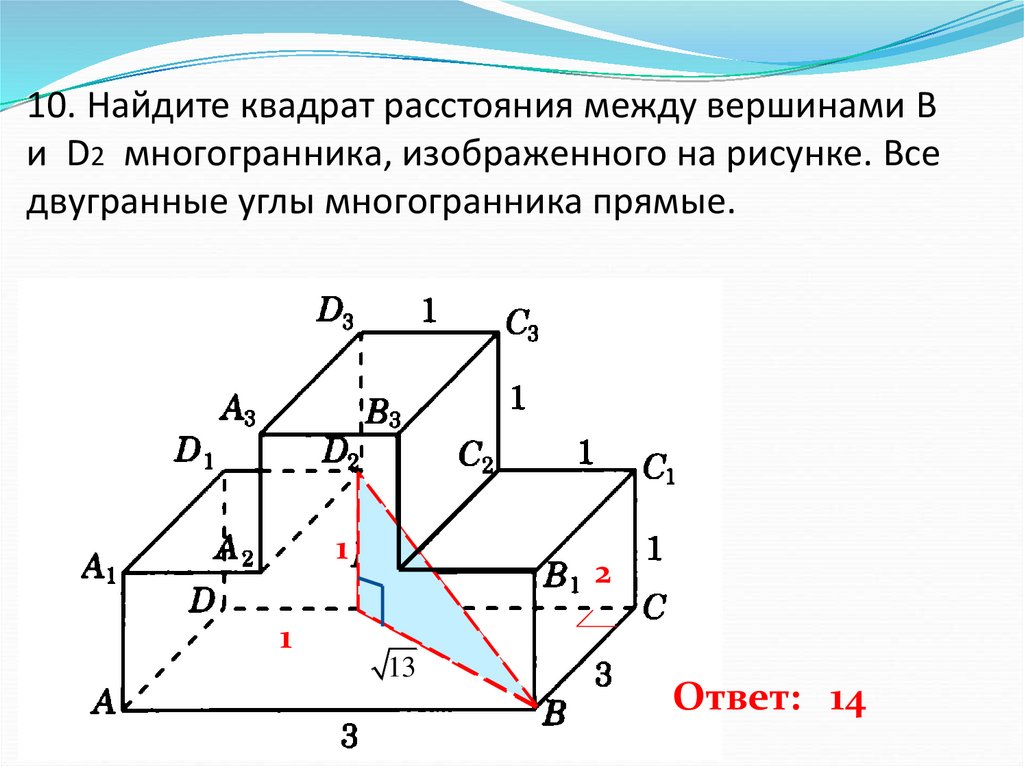
11. 10. Найдите квадрат расстояния между вершинами B и D2 многогранника, изображенного на рисунке. Все двугранные углы

многогранника прямые.
1
2
1
13
Ответ: 14

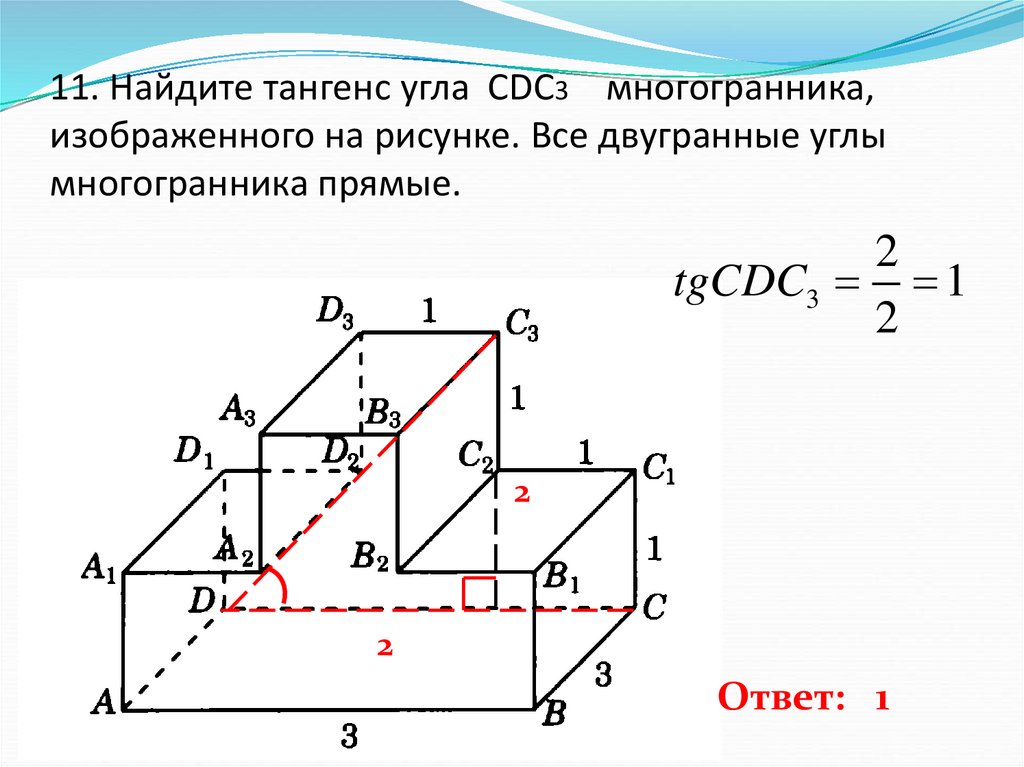
12. 11. Найдите тангенс угла CDC3 многогранника, изображенного на рисунке. Все двугранные углы многогранника прямые.

2
tgCDC3 1
2
2
2
Ответ: 1

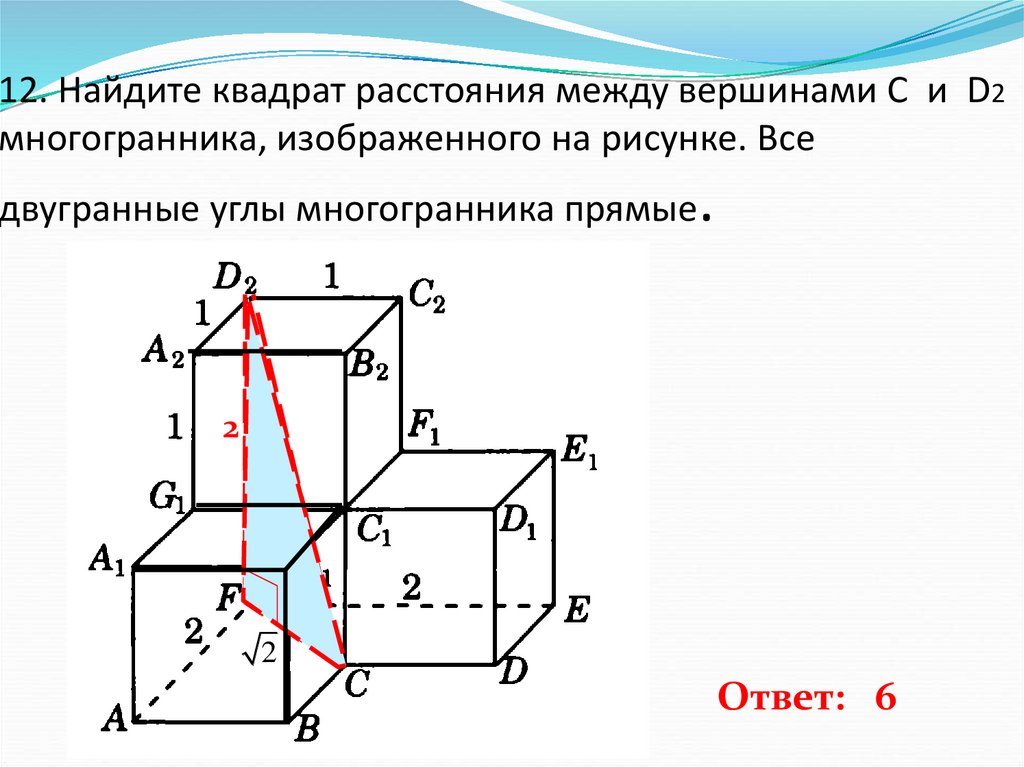
13. 12. Найдите квадрат расстояния между вершинами C и D2 многогранника, изображенного на рисунке. Все двугранные углы

многогранника прямые
.
2
2
Ответ: 6

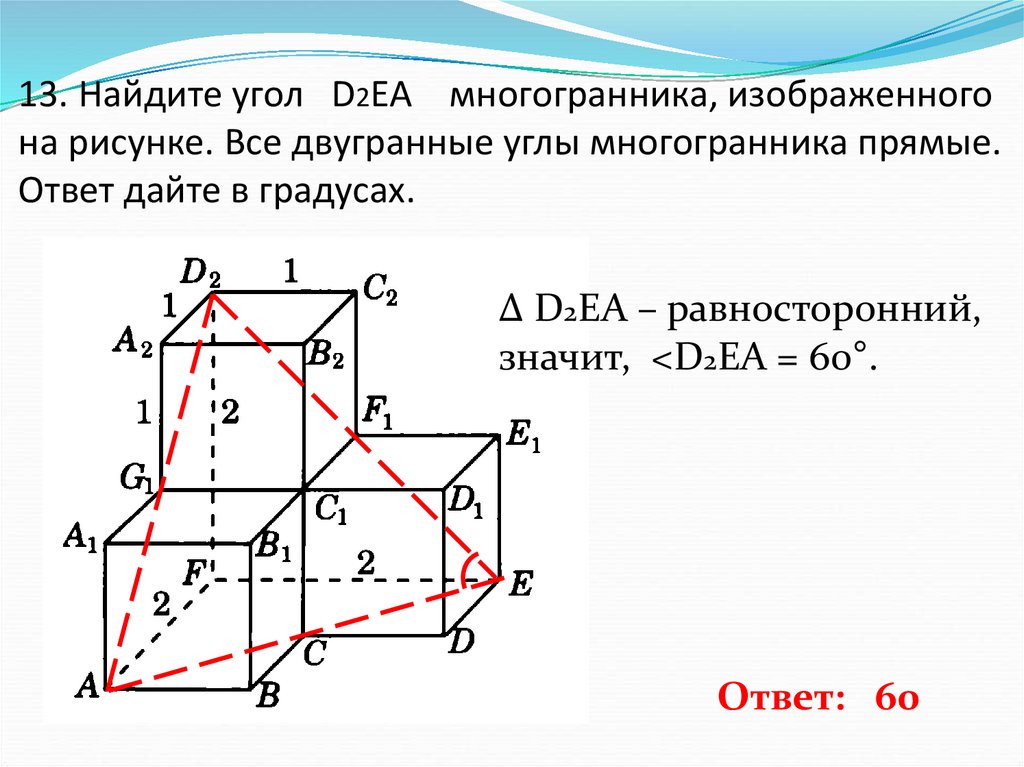
14. 13. Найдите угол D2EA многогранника, изображенного на рисунке. Все двугранные углы многогранника прямые. Ответ дайте в

градусах.
Δ D2EA – равносторонний,
значит, <D2EA = 60°.
Ответ: 60

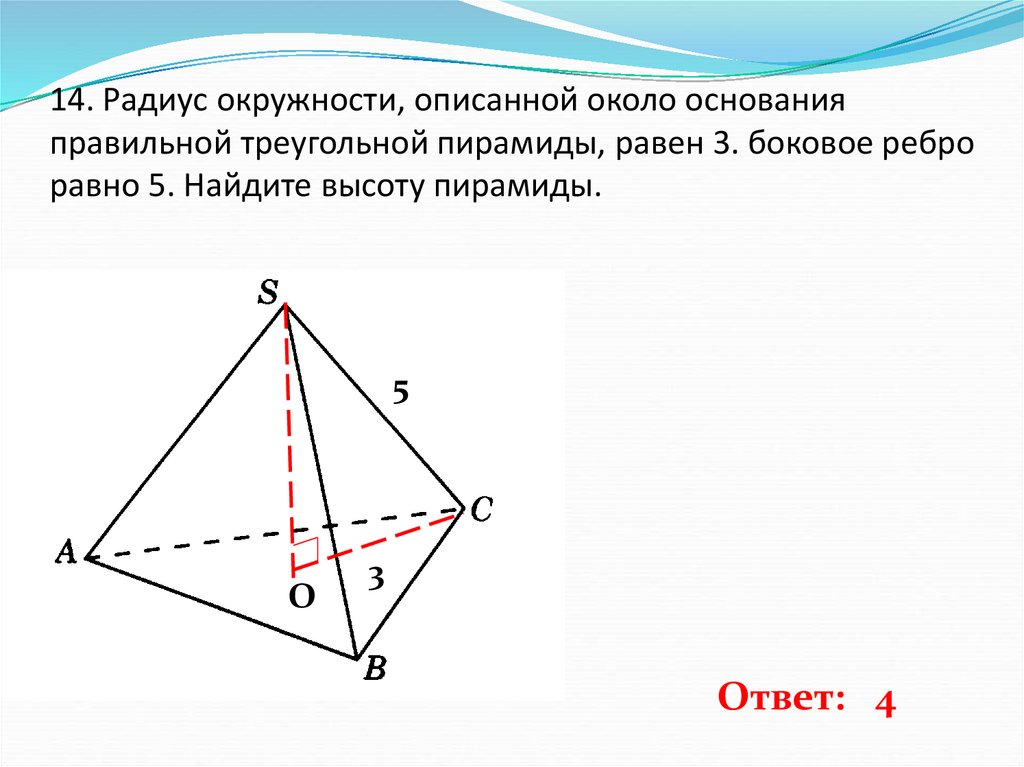
15. 14. Радиус окружности, описанной около основания правильной треугольной пирамиды, равен 3. боковое ребро равно 5. Найдите

высоту пирамиды.
5
О
3
Ответ: 4

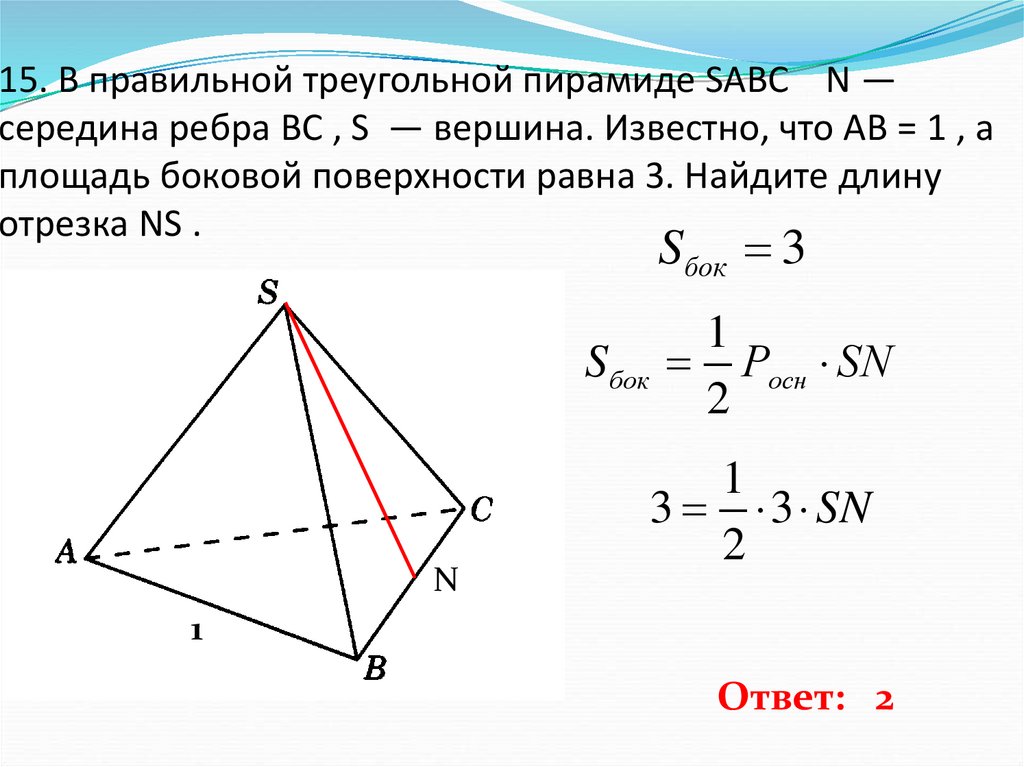
16. 15. В правильной треугольной пирамиде SABC N — середина ребра BC , S  — вершина. Известно, что AB = 1 , а площадь боковой

15. В правильной треугольной пирамиде SABC N —
середина ребра BC , S — вершина. Известно, что AB = 1 , а
площадь боковой поверхности равна 3. Найдите длину
отрезка NS .
Sбок 3
Sбок
N
1
Росн SN
2
1
3 3 SN
2
1
Ответ: 2

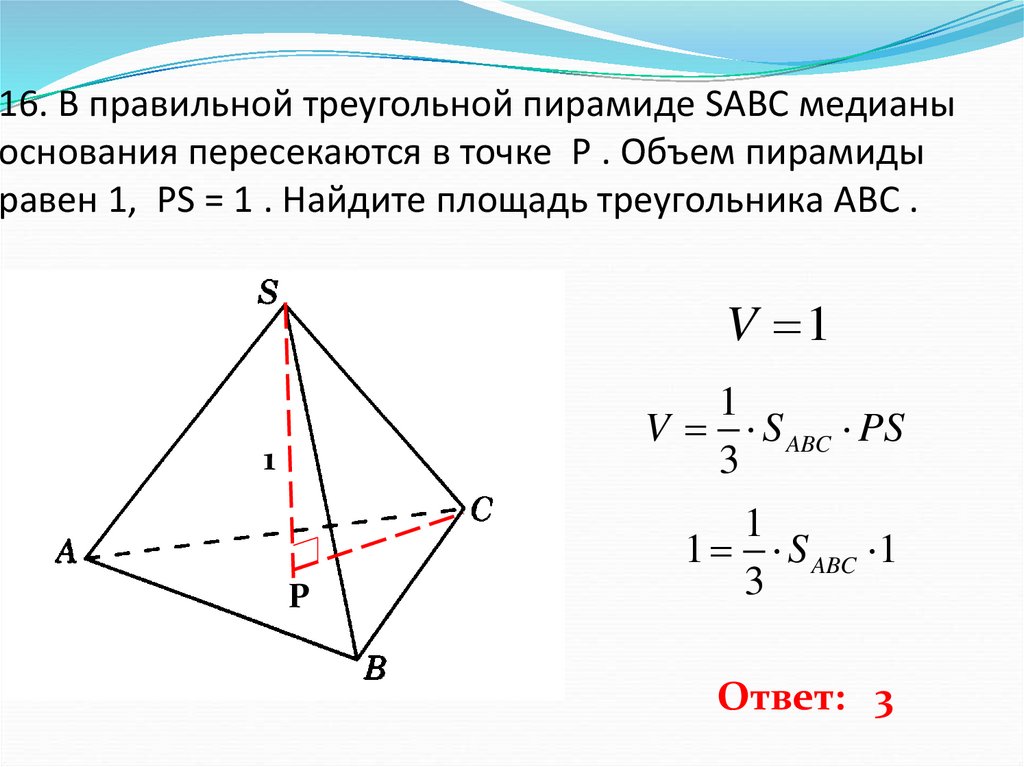
17. 16. В правильной треугольной пирамиде SABC медианы основания пересекаются в точке P . Объем пирамиды равен 1, PS = 1 . Найдите

площадь треугольника ABC .
V 1
1
V S ABC PS
3
1
P
1
1 S ABC 1
3
Ответ: 3

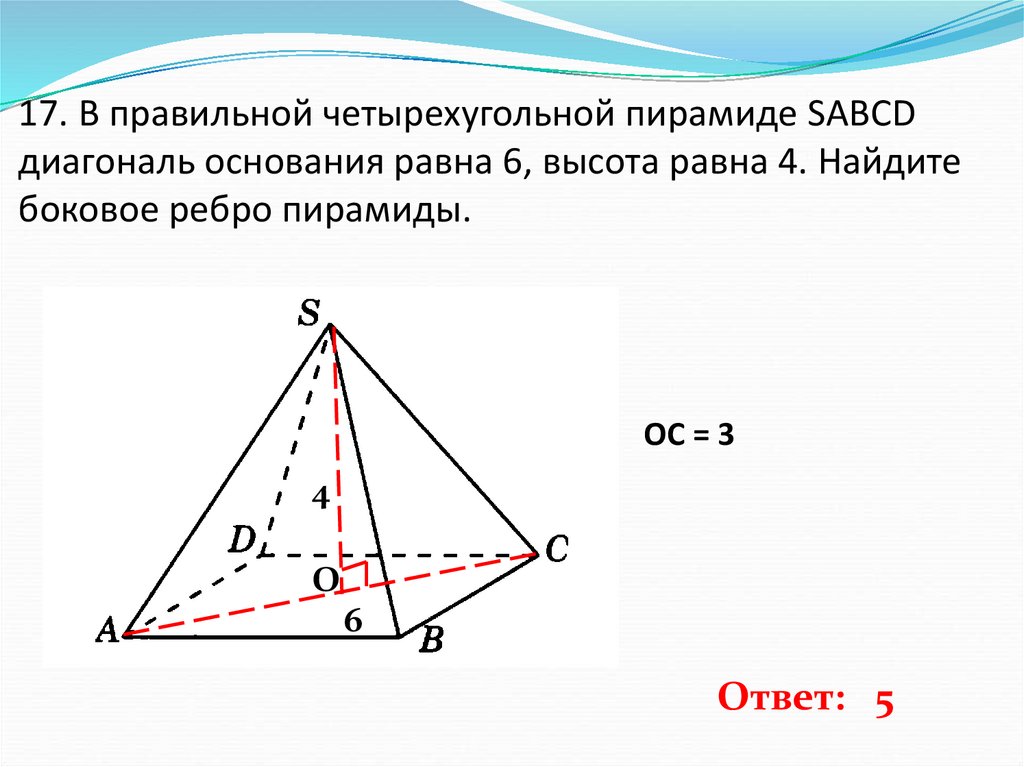
18. 17. В правильной четырехугольной пирамиде SABCD диагональ основания равна 6, высота равна 4. Найдите боковое ребро пирамиды.

ОС = 3
4
О
6
Ответ: 5

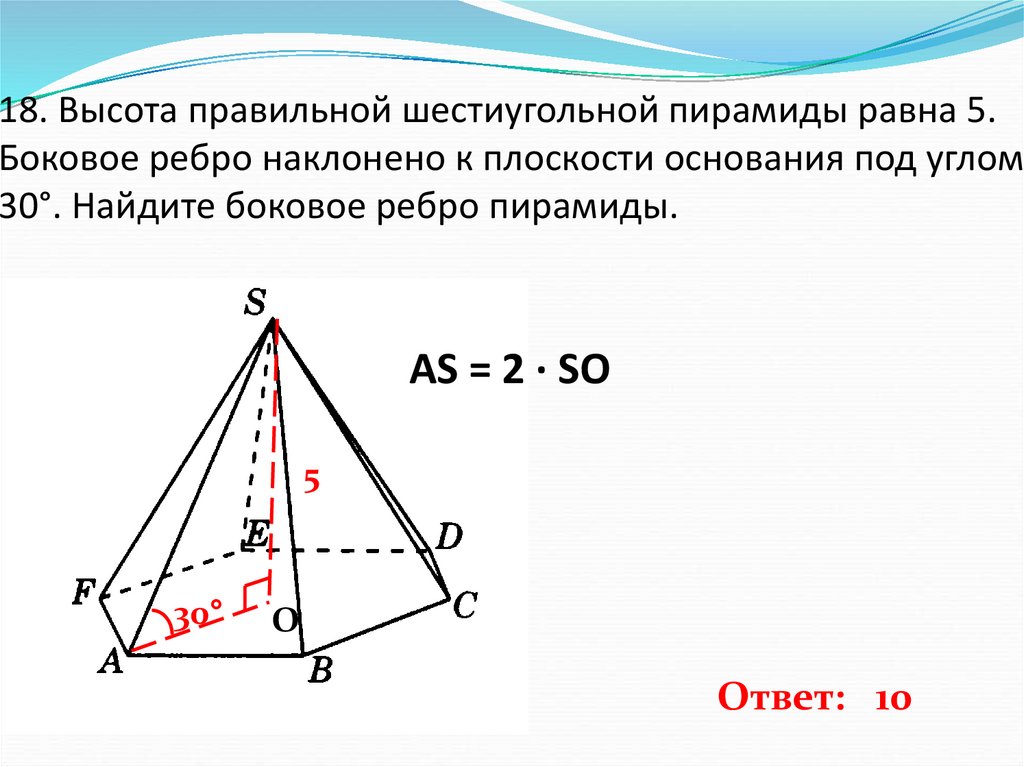
19. 18. Высота правильной шестиугольной пирамиды равна 5. Боковое ребро наклонено к плоскости основания под углом 30°. Найдите

боковое ребро пирамиды.
AS = 2 · SO
5
30°
О
Ответ: 10

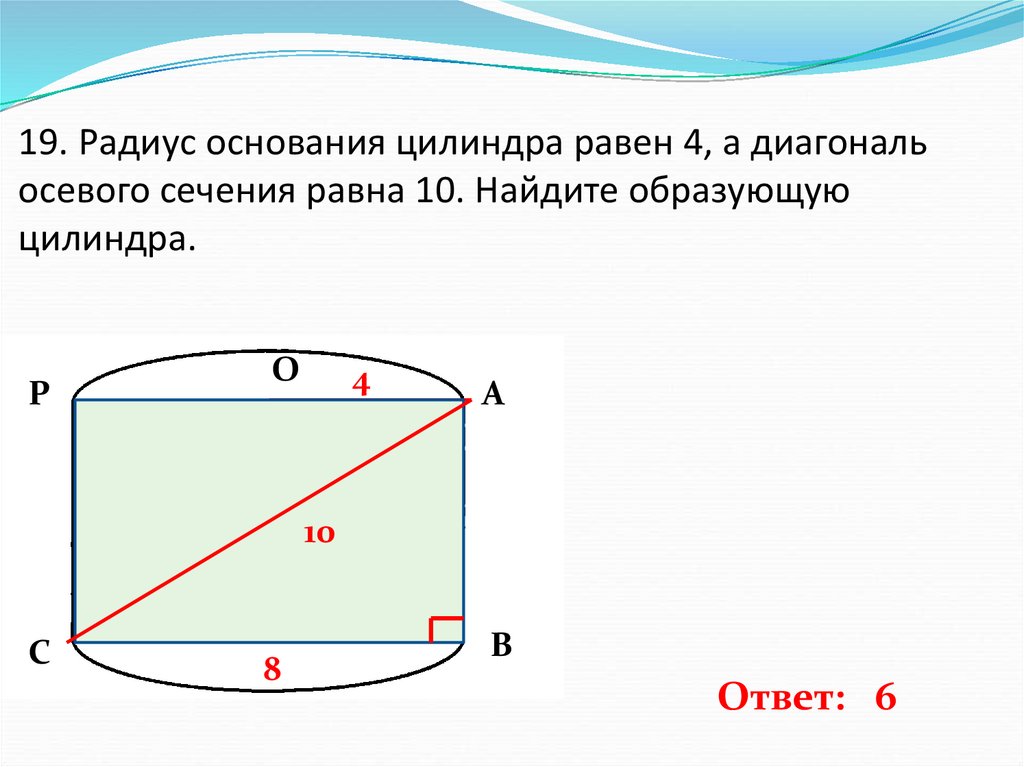
20. 19. Радиус основания цилиндра равен 4, а диагональ осевого сечения равна 10. Найдите образующую цилиндра.

Р
О
4
А
10
С
8
В
Ответ: 6

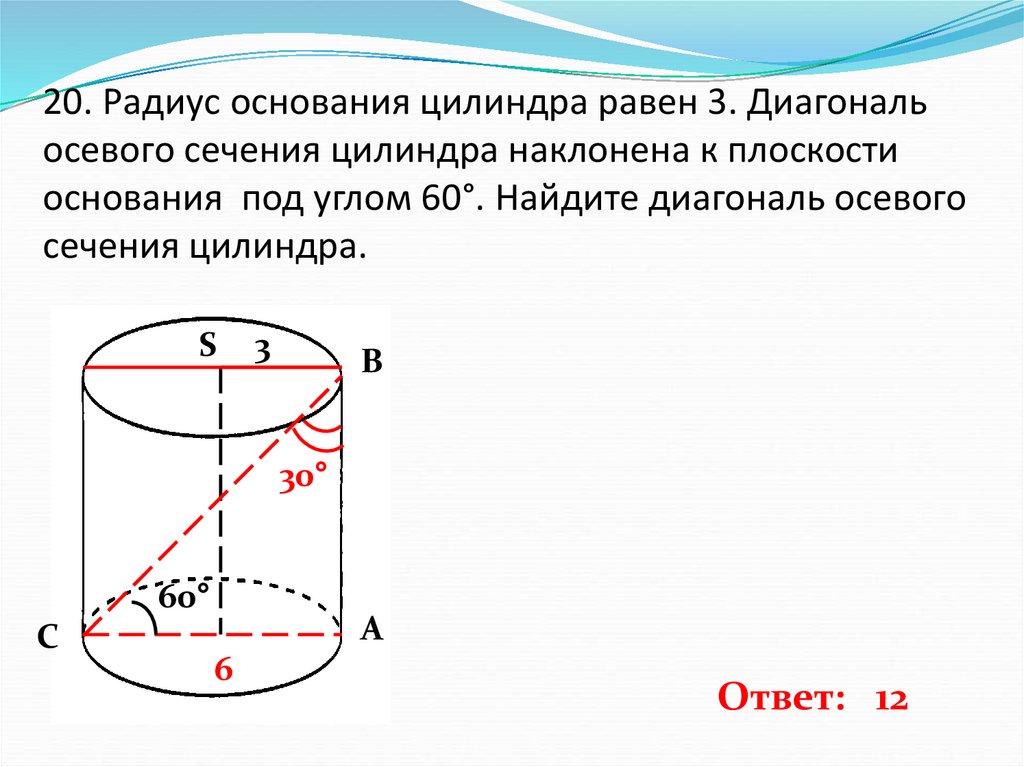
21. 20. Радиус основания цилиндра равен 3. Диагональ осевого сечения цилиндра наклонена к плоскости основания под углом 60°.

Найдите диагональ осевого
сечения цилиндра.
S
3
В
30°
60°
С
А
6
Ответ: 12

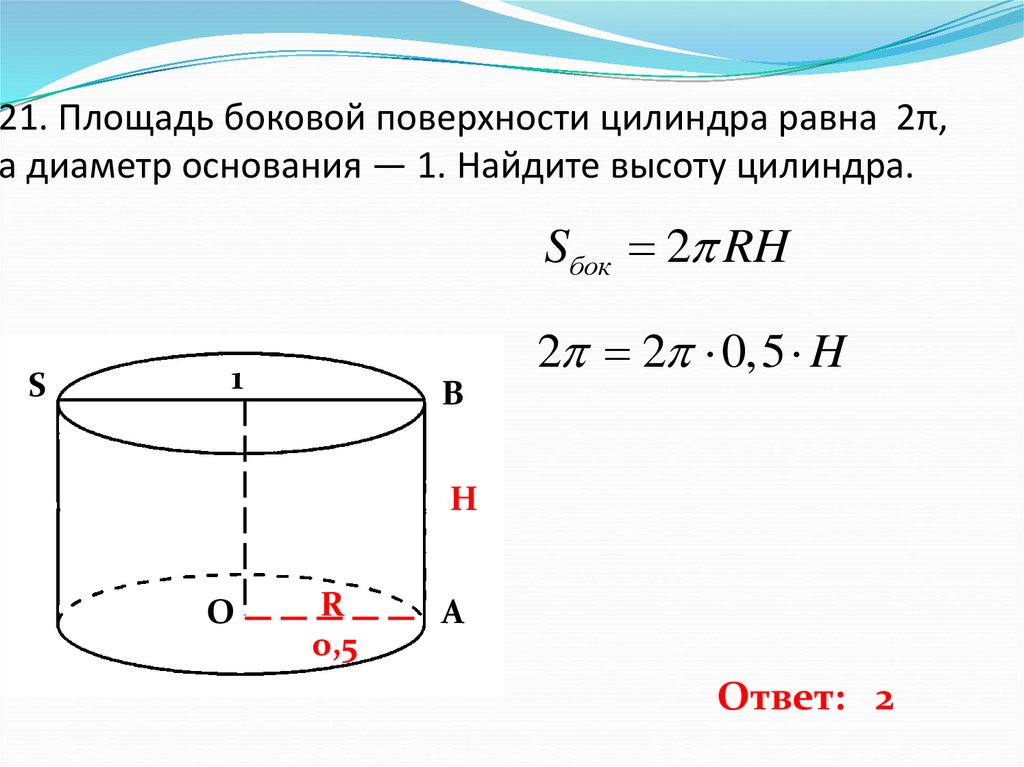
22. 21. Площадь боковой поверхности цилиндра равна 2π, а диаметр основания — 1. Найдите высоту цилиндра.

21. Площадь боковой поверхности цилиндра равна 2π,
а диаметр основания — 1. Найдите высоту цилиндра.
Sбок 2 RH
S
2 2 0,5 H
1
В
H
О
R
0,5
А
Ответ: 2

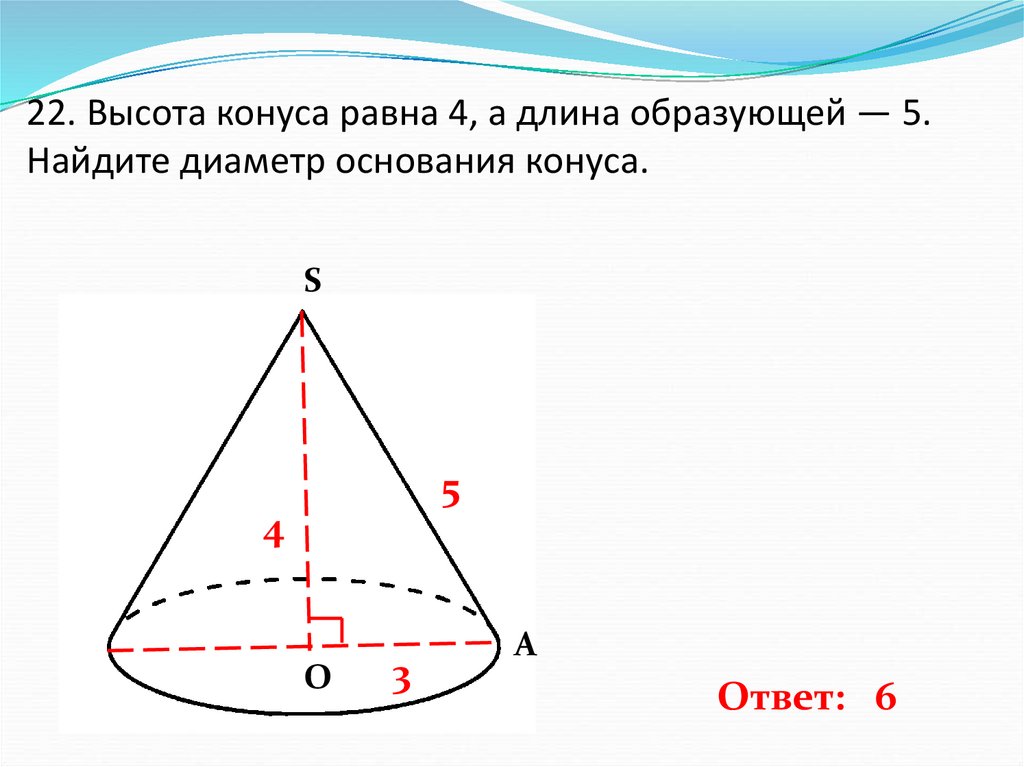
23. 22. Высота конуса равна 4, а длина образующей — 5. Найдите диаметр основания конуса.

22. Высота конуса равна 4, а длина образующей — 5.
Найдите диаметр основания конуса.
S
5
4
O
3
A
Ответ: 6

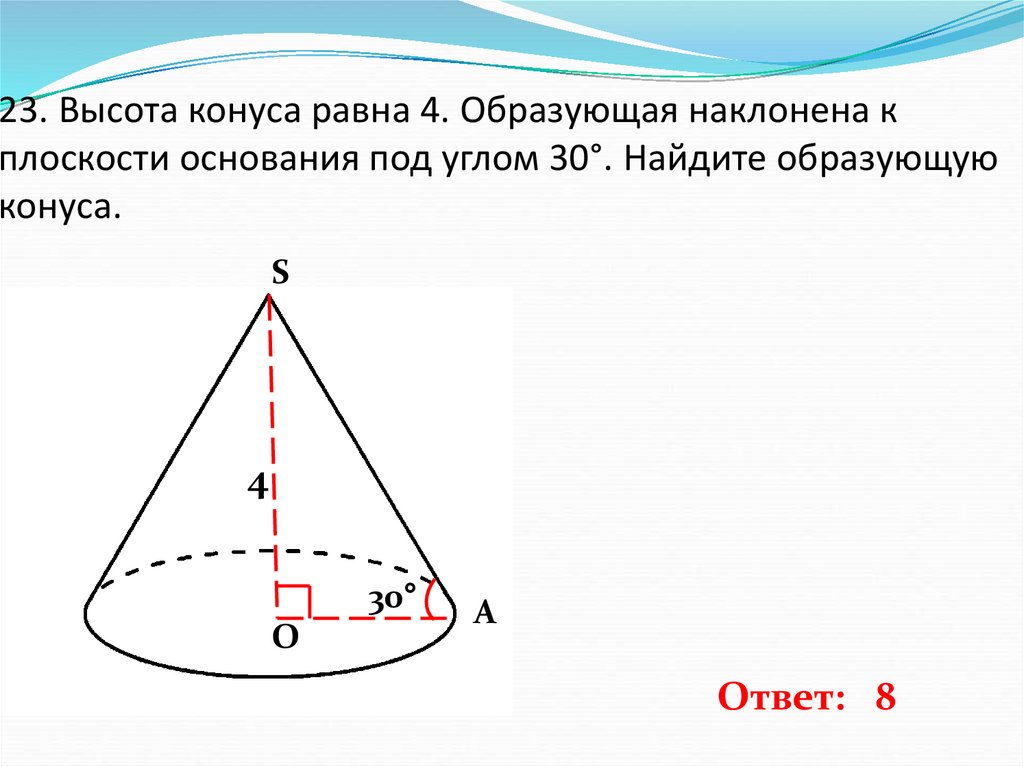
24. 23. Высота конуса равна 4. Образующая наклонена к плоскости основания под углом 30°. Найдите образующую конуса.

S
4
30°
О
А
Ответ: 8

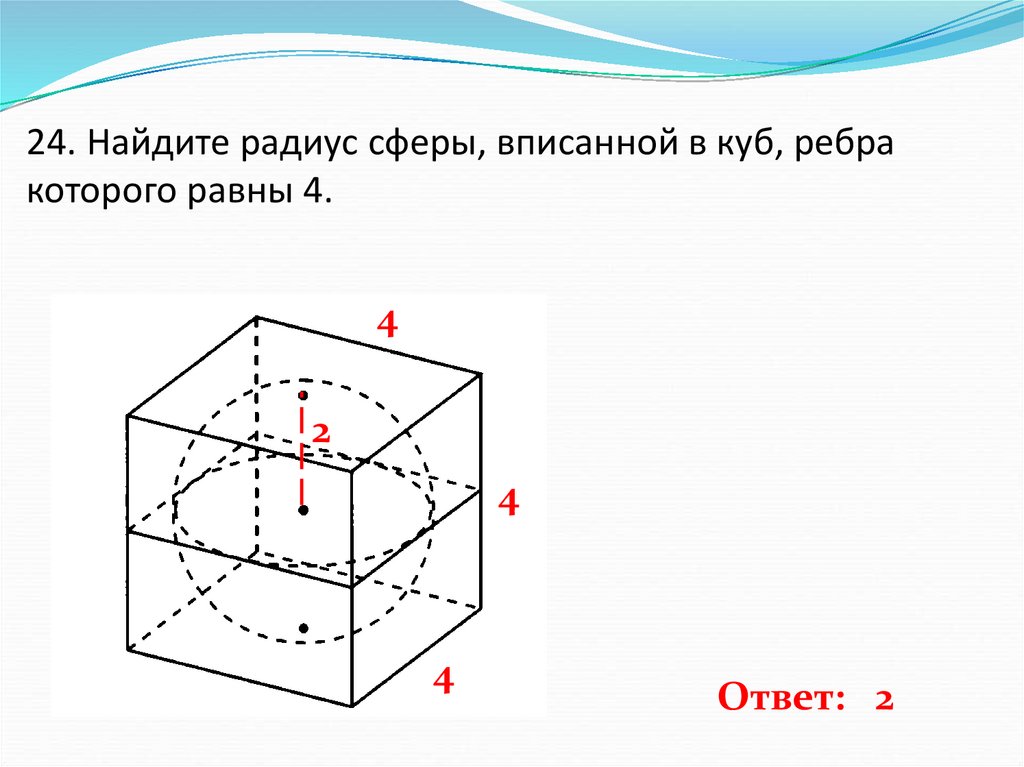
25. 24. Найдите радиус сферы, вписанной в куб, ребра которого равны 4.

4
2
4
4
Ответ: 2

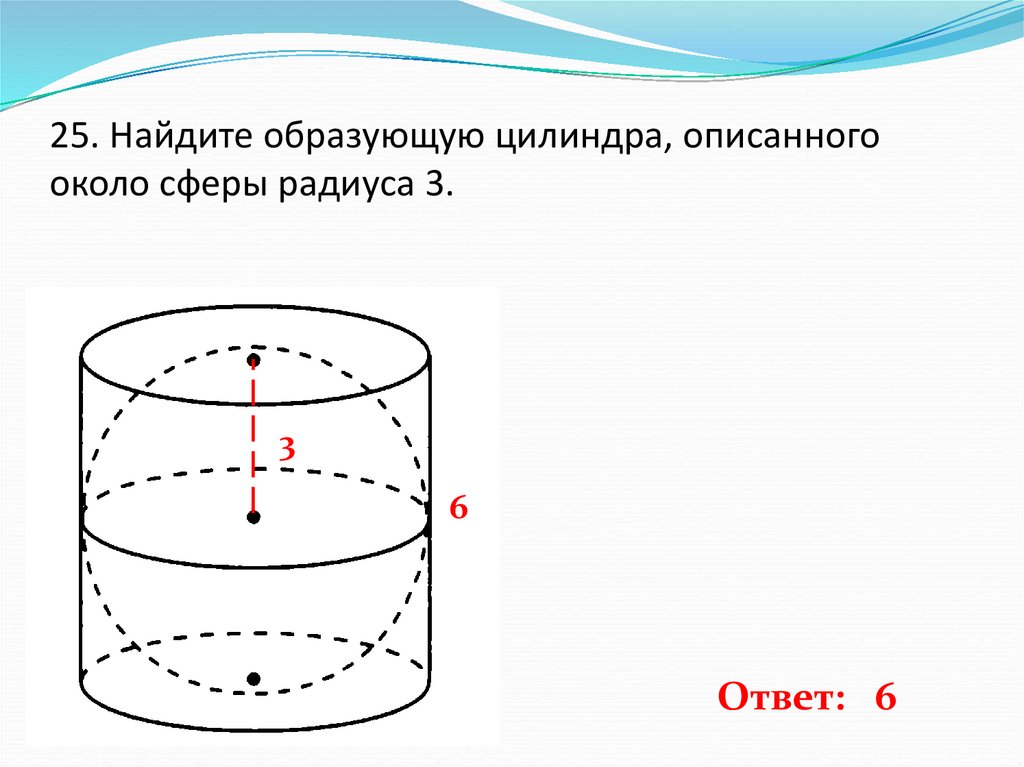
26. 25. Найдите образующую цилиндра, описанного около сферы радиуса 3.

3
6
Ответ: 6

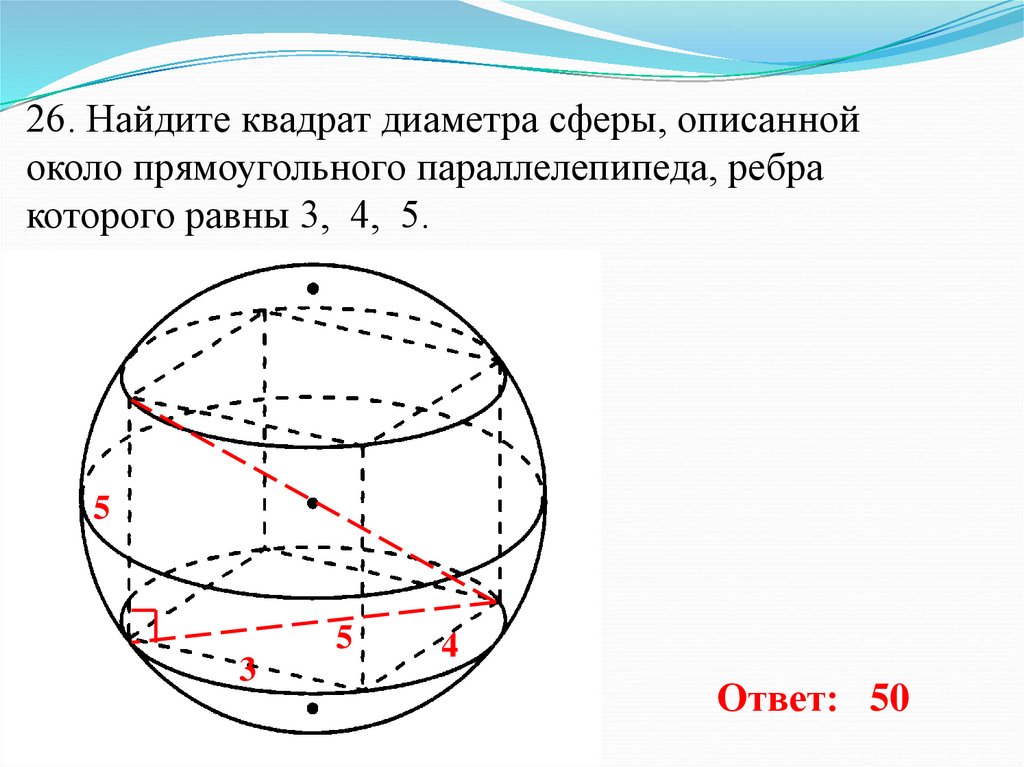
27. 26. Найдите квадрат диаметра сферы, описанной около прямоугольного параллелепипеда, ребра которого равны 3, 4, 5.

5
5
3
4
Ответ: 50

28. Литература:

Открытый банк заданий по математике. ЕГЭ 2012
mathege.ru.
Смирнов В.А. ЕГЭ 2012. Математика. Задача В9.
Стереометрия: расстояния в пространстве. Рабочая
тетрадь. Москва. Издательство МЦНМО. 2012.