Похожие презентации:
Касательная к окружности
1.
Касательная к окружности2.
Здравствуйте, господа!Сегодня мы с вами продолжаем
изучать окружность. Только
окружность рассмотрим в паре с
прямой, т.е. различные
комбинации окружности и прямой.
3.
В тетрадь:16.04.20
Классная работа.
Касательная к окружности.
4.
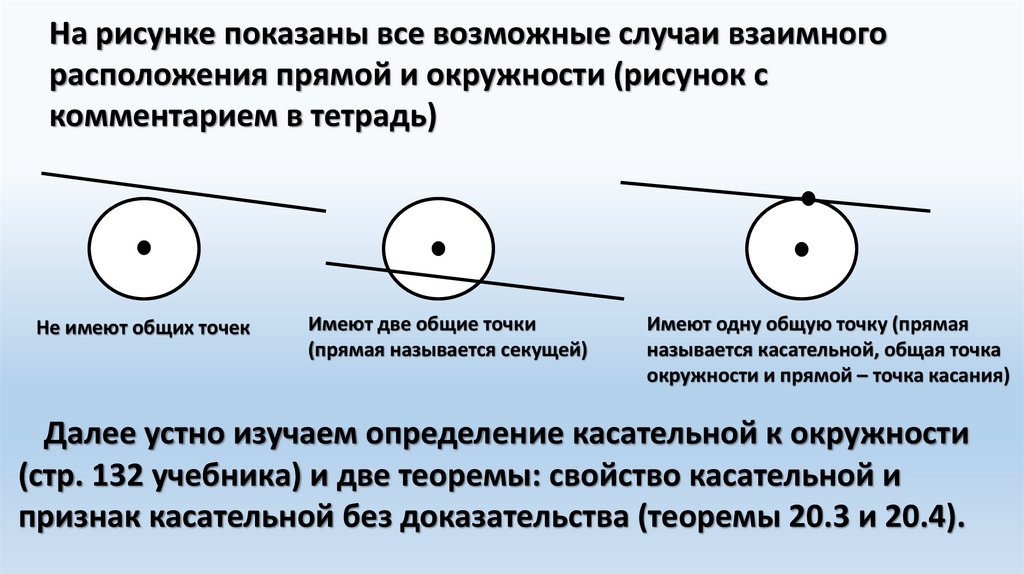
На рисунке показаны все возможные случаи взаимногорасположения прямой и окружности (рисунок с
комментарием в тетрадь)
Не имеют общих точек
Имеют две общие точки
(прямая называется секущей)
Имеют одну общую точку (прямая
называется касательной, общая точка
окружности и прямой – точка касания)
Далее устно изучаем определение касательной к окружности
(стр. 132 учебника) и две теоремы: свойство касательной и
признак касательной без доказательства (теоремы 20.3 и 20.4).
5.
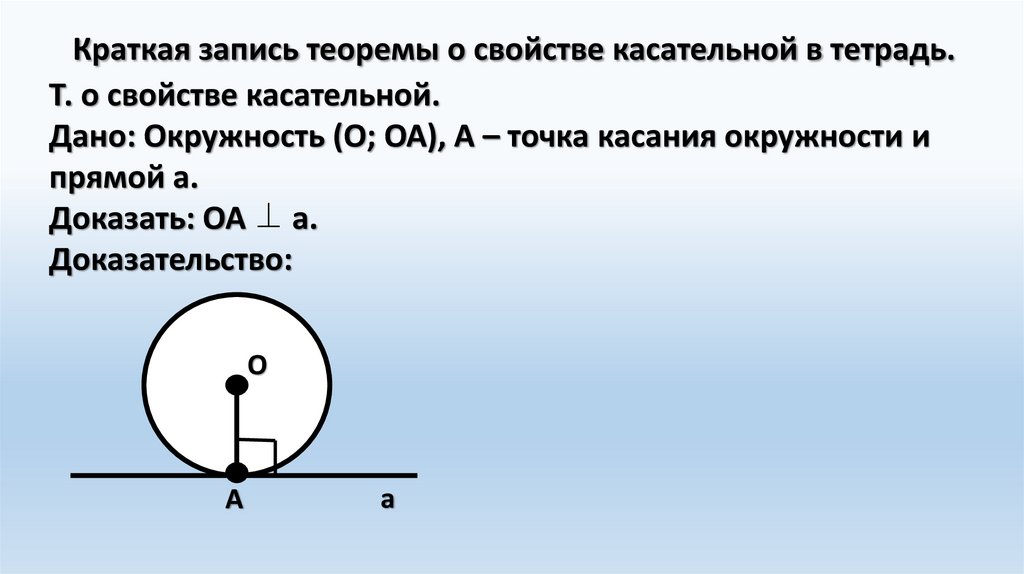
Краткая запись теоремы о свойстве касательной в тетрадь.Т. о свойстве касательной.
Дано: Окружность (О; ОА), А – точка касания окружности и
прямой а.
Доказать: ОА а.
Доказательство:
О
О
А
а
6.
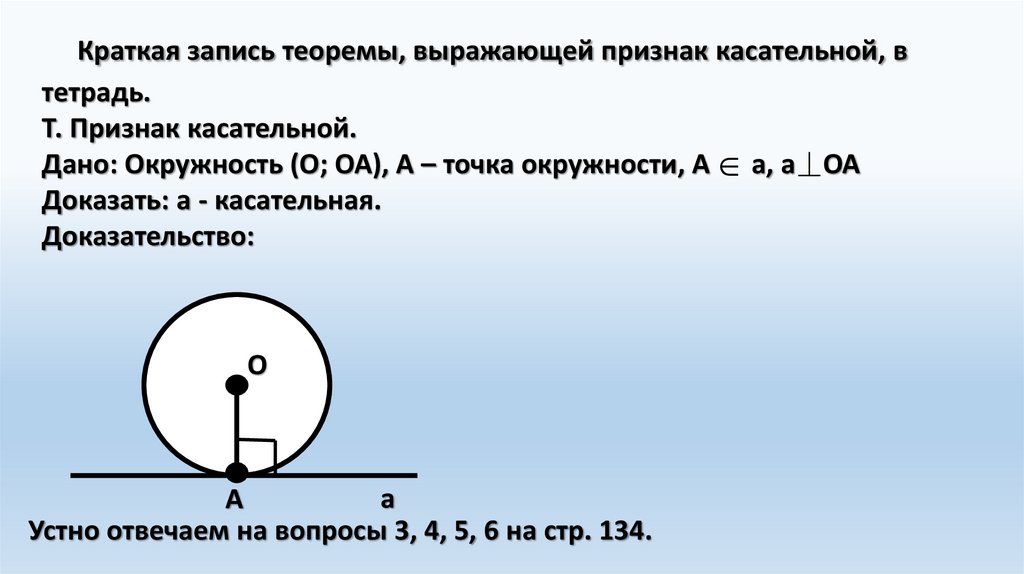
Краткая запись теоремы, выражающей признак касательной, втетрадь.
Т. Признак касательной.
Дано: Окружность (О; ОА), А – точка окружности, А а, а ОА
Доказать: а - касательная.
Доказательство:
О
О
а
А
Устно отвечаем на вопросы 3, 4, 5, 6 на стр. 134.
7.
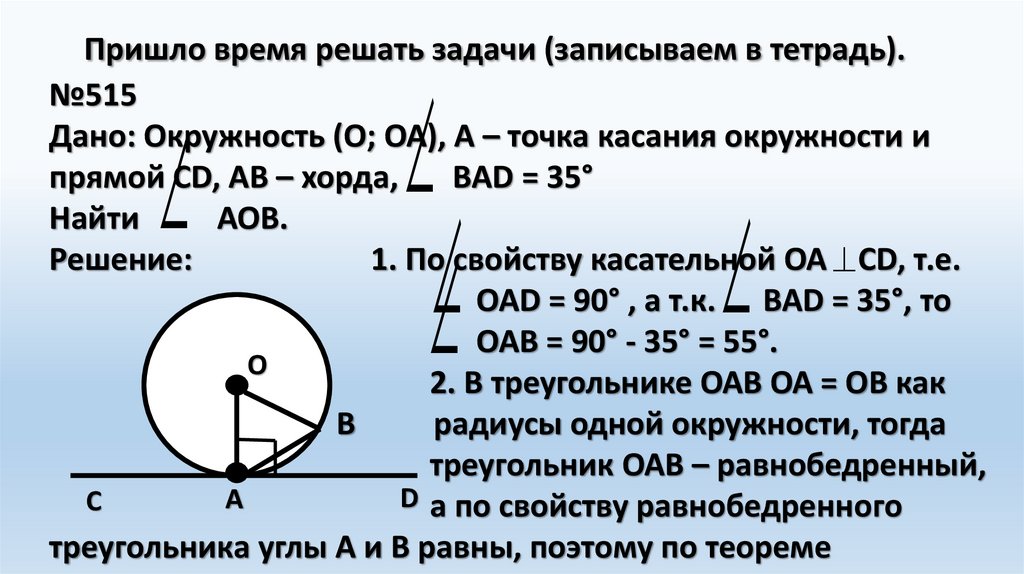
Пришло время решать задачи (записываем в тетрадь).№515
Дано: Окружность (О; ОА), А – точка касания окружности и
прямой CD, АВ – хорда,
BAD = 35°
Найти
АОВ.
Решение:
1. По свойству касательной ОА CD, т.е.
ОАD = 90° , а т.к. BAD = 35°, то
ОАВ = 90° - 35° = 55°.
О
О
2. В треугольнике ОАВ ОА = ОВ как
В
радиусы одной окружности, тогда
треугольник ОАВ – равнобедренный,
D а по свойству равнобедренного
А
С
треугольника углы А и В равны, поэтому по теореме
8.
о сумме углов треугольника- 55° · 2 = 70°.
Ответ. АОВ = 70°
АОВ = 180° -
9.
Дома. §20 (стр. 132 – 133 до задачи), №516.На этом урок окончен.
Работы присылать сегодня в личное
сообщение в Vk.
Очень надеюсь, что скоро увидимся!!!




 Математика
Математика








