Уравнения Максвелла

1. Уравнения Максвелла

Вихревое электрическое поле. Первое уравнение
Максвелла
Ток смещения.
Уравнения Максвелла в интегральной форме
Уравнения Максвелла в дифференциальной форме
Материальные уравнения
Электромагнитные волны

2. Вихревое электрическое поле. Первое уравнение Максвелла

Основные утверждения, которые поучили при изучении электрических
и магнитных поле:
Электростатическое поле создается неподвижными зарядами. Силовые
линии электростатического поля начинаются и заканчиваются на зарядах (
или в бесконечности). Математически запись этого утверждения – теорема
Остроградского-Гаусса для электростатических полей:
E dS
S
1
dV
0 V
Магнитные заряды отсутствуют, линии индукции магнитного поля замкнуты.
Математическая запись этого утверждения – теорема Гаусса для магнитного
поля:
B dS 0
S

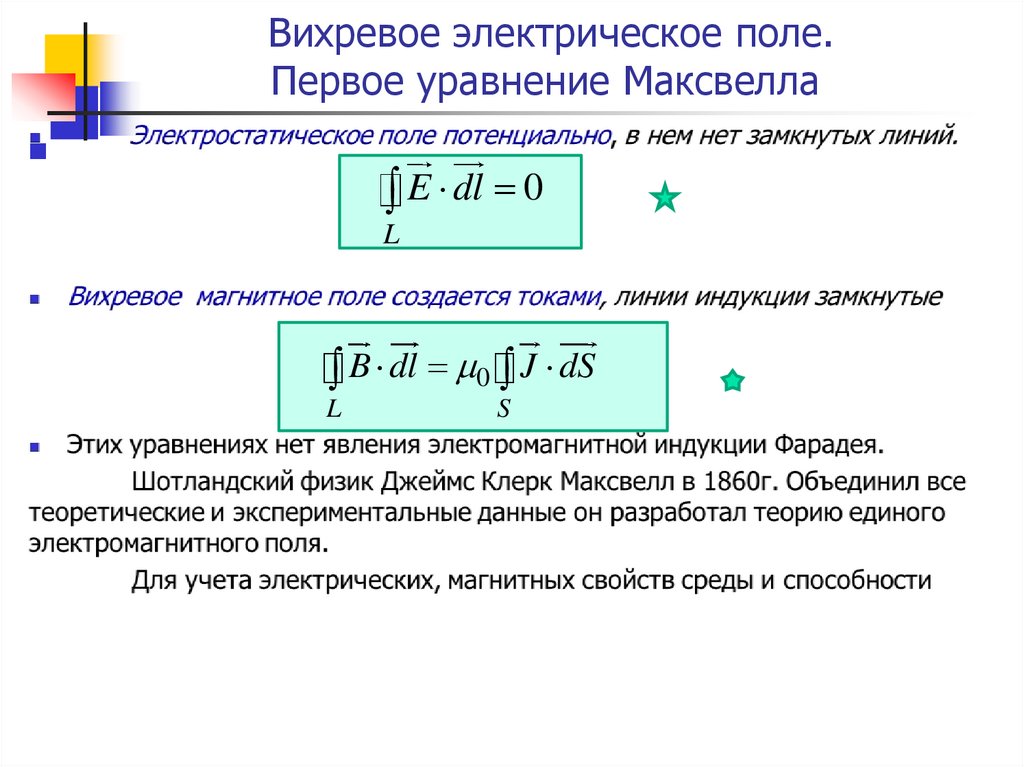
3. Вихревое электрическое поле. Первое уравнение Максвелла

E dl 0
L
B dl 0 J dS
L
S

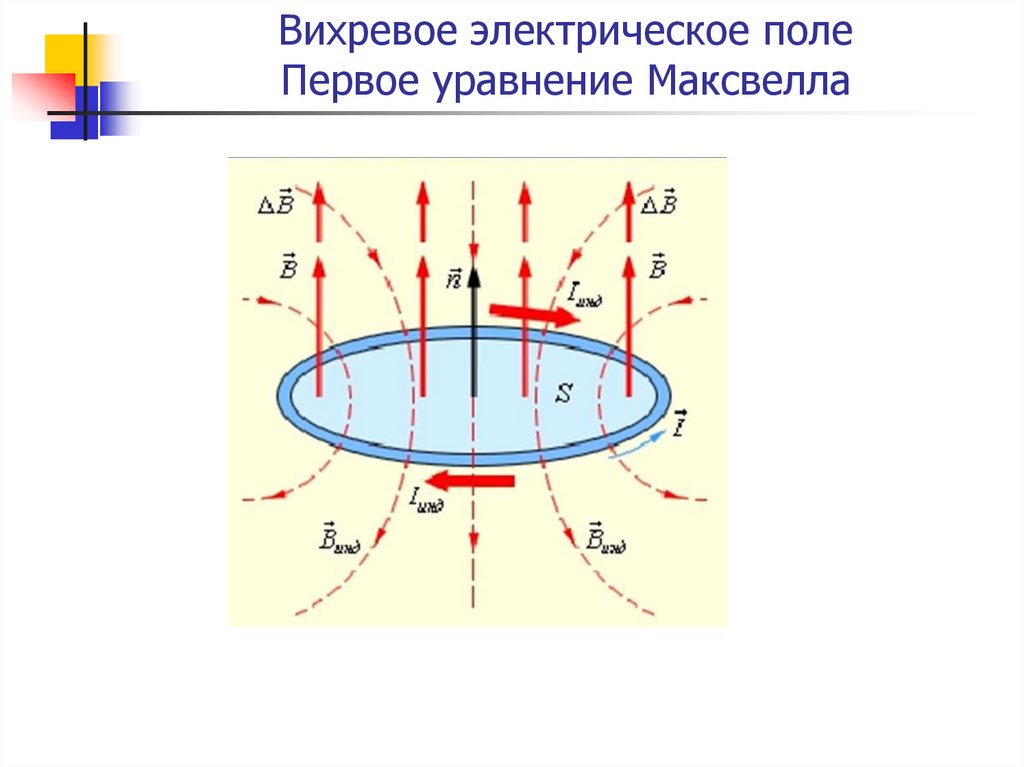
4. Вихревое электрическое поле. Первое уравнение Максвелла

E dl 0
L
ФB
i E i dl
t
L

5. Вихревое электрическое поле. Первое уравнение Максвелла

dФ
B
B
i E i dl
B dS
dS
dt
t S
L
S t
• Объединяя все положения, получим, что изменяющееся магнитное поле
приводит к появлению вихревого электрического поля:
E dl
L
S
B
dS
t
это первое уравнение Максвелла.
• Если в контуре есть источники ЭДС, то уравнение примет вид:
N
B
E dl t dS k
k 1
L
S
• Циркуляция как вихревого, так и электростатического поля.
• Первое уравнение Максвелла показывает, что источником электрического
поля могут быть не только электрические заряды, но и изменяющееся во
времени магнитное поле

6. Вихревое электрическое поле Первое уравнение Максвелла

7. Ток смещения Второе уравнения Максвелла

Теперь надо откорректировать четвертое уравнение (со звездочкой), так
как нарушена симметрия между электрическим и магнитным полем.
Мы установили , что изменение магнитного поля, влечет появление вихревого
электрического поля. Можно ожидать, что меняющееся со временем
электрическое поле создаст магнитное поле.
Согласно теореме о циркуляции вектора индукции
магнитного поля ( или напряженности магнитного
поля) – закон полного тока:
H dl j dS
L
L
S
B dl 0 ( I макро I микро )
R
L
В первом уравнении плотность макротоков, а во втором макро- и микротоки.
Применим эту теорему к случаю, когда предварительно заряженный
конденсатор, разряжается через внешнее сопротивление. На контур L можно
натянуть любую поверхность S S
1 2

8. Ток смещения Второе уравнения Максвелла

Через поверхность S1 течет ток, а через
поверхность S не течет. Получается, что циркуляция
2
зависит от выбора поверхности. Поверхность S 2
пронизывается только электрическим полем, по теореме
L
Гаусса поток вектора индукции через замкнутую поверхность S 2 равен:
ФD D dS qсвоб
q
S2
D dS
Продифференцируем это равенство по времени: t
t
S2
Если поверхность S2 неподвижная и не деформируется, то изменение потока
связано с изменением индукции магнитного поля D , запишем:
D dS
S
q
(1)
t
j dS
- теорема Гаусса
q
(2) - уравнение непрерывности
t
Сложим эти два уравнения:
D
j t dS 0 (3)

9. Ток смещения Второе уравнение Максвелла

D
j t dS 0 (3)
Это уравнение аналогично уравнению непрерывности для постоянного
тока. Откуда видно, что кроме плотности тока проводимости, имеется еще одно
слагаемое - D - размерность этого слагаемого, соответствует плотности тока.
t
D
j
Максвелл ввел понятие тока смещения - см
t - плотность тока смещения в
данной точке пространства равна скорости изменения вектора электрического
смещения в этой точке.
Током смещения сквозь замкнутую поверхность называется физическая величина
численно равная потоку вектора плотности тока смещения сквозь эту поверхность:
I см
S
D
D
j dS
dS , тогда для полного тока : j
полн j пров
t
S
t
Из уравнения линии полного тока являются непрерывными, в отличии от тока
проводимости. Токи проводимости замыкаются токами смещения.

10. Ток смещение Второе уравнение Максвелла

D
H dl j t dS
L
S
Это уравнение справедливо всегда.
• Ток смещения, как и ток проводимости способен создавать магнитное поле.
D 0 E Pe jсм
D
E Pe
0
t
t
t
• Первое слагаемое – ток смещения в вакууме, второе – ток связанный с
поляризацией, обусловлен движением связанных зарядов.
E
0
• Принципиально новое утверждение Максвелла, что часть тока смещения
t ,
которая не связана с движением зарядов, а обусловлена только изменением
электрического поля, также возбуждает магнитное поле, даже в вакууме.
• Второе уравнение Максвелла показывает, что магнитные поля могут
возбуждаться либо движущимися электрическими зарядами ( электрическими
токами), либо переменным электрическим полем.
Введение понятия тока смещения завершило создание блестящей теории
электромагнитного поля.

11. Ток смещения Второе уравнения Максвелла

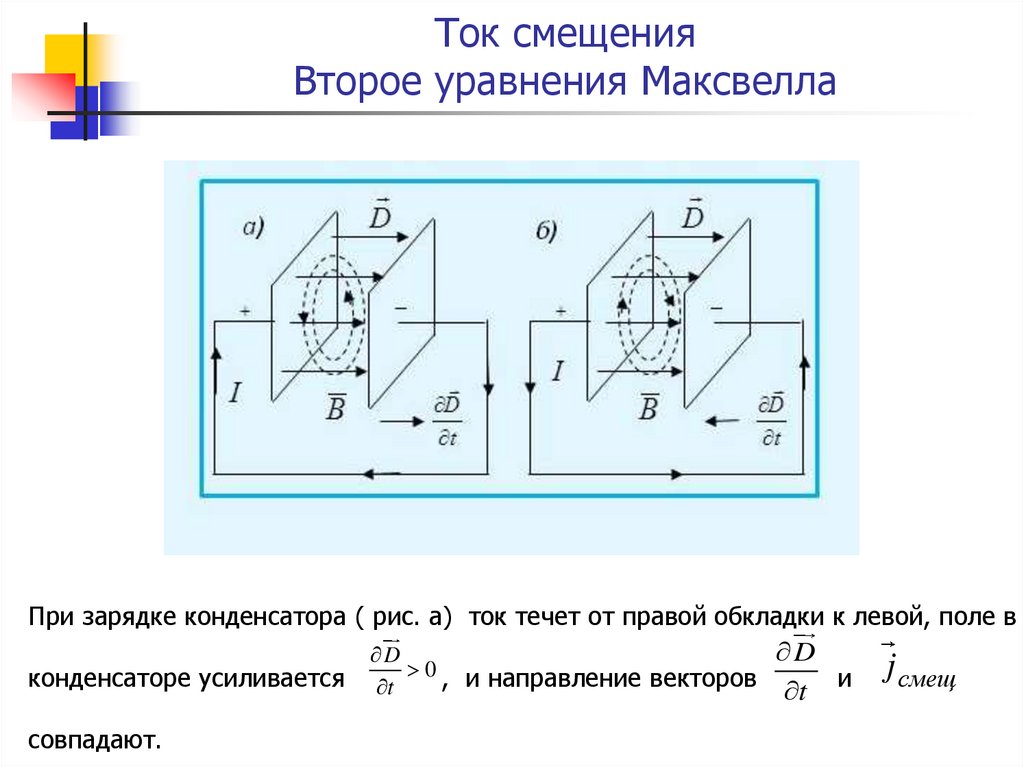
При зарядке конденсатора ( рис. а) ток течет от правой обкладки к левой, поле в
конденсаторе усиливается
совпадают.
D
D
0 , и направление векторов
t
t и
j смещ

12. Уравнения Максвелла в интегральной форме

1) H dl
L
S
D
j пров dS
dS
S t
- Закон полного тока
B
2) E dl
dS
L
S t
- Закон электромагнитной индукции
3) D dS dV qсвоб
- Теорема Гаусса
S
V
4) B dS 0
- Теорема Гаусса
S
Материальные уравнения:
D 0 E
B 0 H
j E
- Для полей в веществе надо добавить
материальные уравнения, которые
характеризуют электрические и
магнитные свойства среды
-
E E эл E стор

13. Уравнения Максвелла в интегральной форме

Уравнения Максвелла силовыми и энергетическими соотношениями:
F qE q B
w
1
D E B H
2
- сила Лоренца, действующая на частицу в
электрическом и магнитном поле
- плотность энергии электромагнитного поля
И граничными условиями:
E 1 E 2 Dn1 Dn 2
H 1 H 2 Bn1 Bn 2

14. Уравнения Максвелла для стационарных полей

Edl
Если же поля стационарны E const и B const , то уравнения
Максвелла распадаются на две группы независимых уравнений:
0
DdS 0
Hdl I
BdS 0
В этом случае электрическое и магнитное поля независимы друг от друга,
что позволяет изучить сначала постоянное электрическое поле, а затем
независимо от него и постоянное магнитное поле.

15. Уравнения Максвелла в дифференциальной форме

Для перехода от интегральной к дифференциальной
форме, вспомним некоторые понятия из векторного анализа:
Оператор «дивергенция» – под дивергенцией векторного поля
А(x,y,z) понимается скалярное поле вида:
Ax Ay Az
div A
x
y
z
div A
A dS
lim
V 0
s
V
An dS div A dV
S
V
Dn dS qсвоб dV divD dV
S
V
divD divE
- связь дивергенции
векторного поля с
потоком этого поля
V
0
div – расхождение (лат), описывает конфигурацию силовых линий типа «ежа»,
расходящихся из точки ( где имеется электрический заряд, источник поля)

16. Уравнения Максвелла в дифференциальной форме

Оператор «ротор» – под ротором векторного поля
Az Ay Ax Az
rot A
i
z z
x
y
rot A
A dl
Ay Ax
j x y k
lim S Al dl rot A n dS
S 0
L
S
L
Bn
E dl t dS rot E dS
L
S
S
rot E
Теорема Стокса: циркуляция
вектора по замкнутому
контуру равна потоку ротора
вектора
B
t
rot – вращение – кольцеобразные силовые линии вокруг источника ( тока
или полей меняющихся во времени)

17. Уравнение Максвелла в дифференциальной форме

D
H dl j пр t dS rot H dS
L
S
S
D
rot H j пр
t
B dl 0 Ii 0 j dS
L
i
rot B 0 j jсм
S

18. Уравнения Максвелла в дифференциальной форме

Уравнения Максвелла можно представить в дифференциальной форме:
E B / t
D
rot E B / t
divD
Эти уравнения говорят о том, что электрическое поле может возникнуть
по двум причинам. Во-первых, его источником являются электрические
заряды, как сторонние, так и связанные. Во-вторых, поле образуется
всегда, когда меняется во времени магнитное поле.
H j D / t
B 0
rot H j D / t
divB 0
Эти уравнения говорят о том, что магнитное поле может возбуждаться
либо движущимися электрическими зарядами (электрическими токами),
либо переменными электрическими полями, либо тем и другим
одновременно.

19. Уравнения Максвелла в дифференциальной форме

E B / t
B 0
H D / t
D 0
rot 0

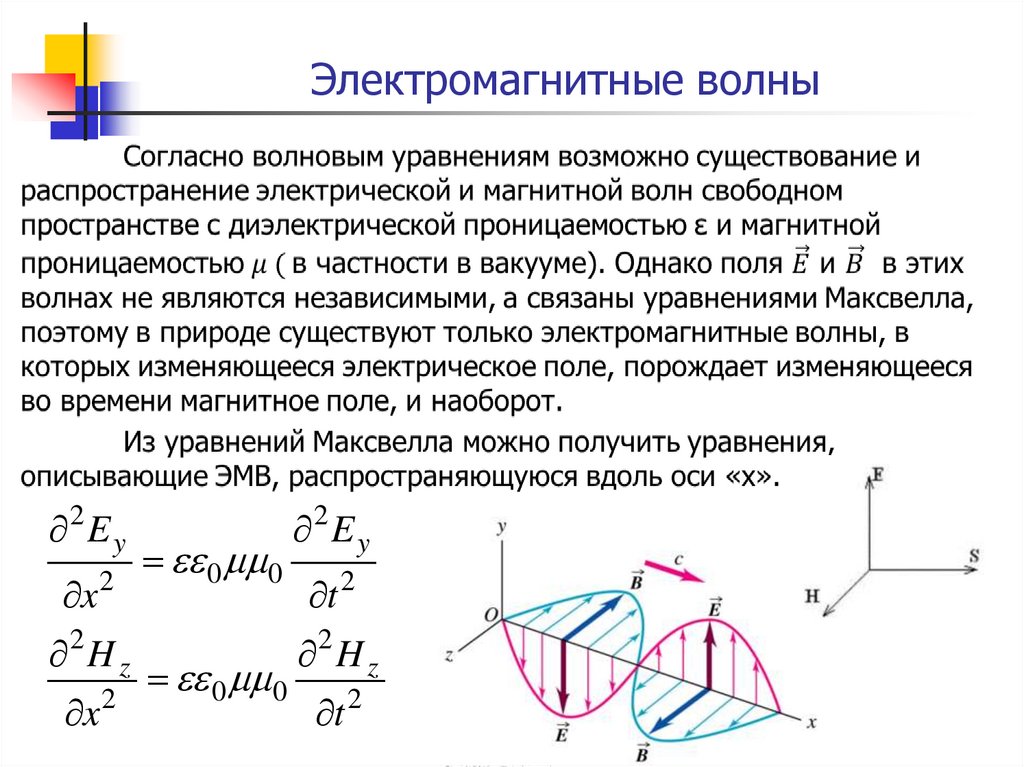
20. Электромагнитные волны

К юбилею Максвелла один из научных журналов написал:
«И сказал Бог:
divD
divB 0
rot E B / t
E
rot B 0 j 0
t
и стал «СВЕТ»
Свет – электромагнитная волна.
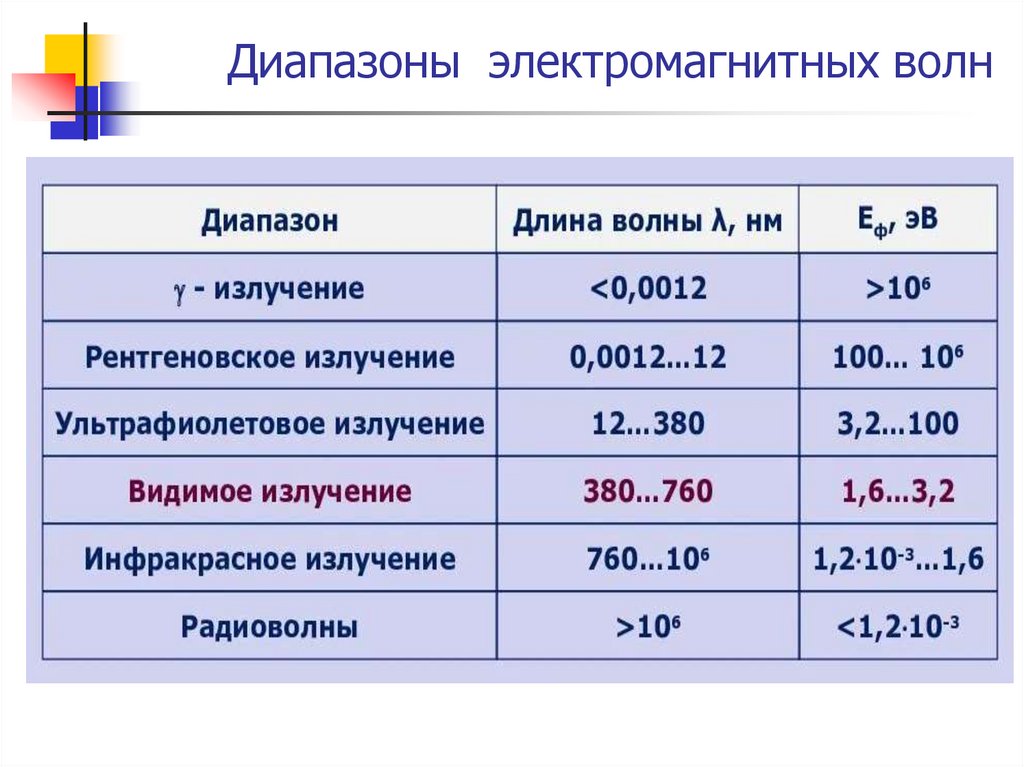
ЭМВ обладают широким диапазоном частот ( и длин волн) -
где c- скорость ЭМВ в вакууме.
с

21. Электромагнитные волны

Запишем уравнения Максвелла для среды, где нет свободных зарядов и
током проводимости, с учетом, что :
D E и B 0 H
0
E
1) E 0
2) B 0
B
t
B 0 0
E
t
2 E
E
B 0 0 2
t
t
2 B
B 0 0 ( E ) 0 0 2
t
t
E E E E
a b c b a c c a b
2
x
2
2
y
2
2
z 2
Умножим обе части этих уравнений
векторно слева на оператор набла:
Левая часть этих уравнений двойное
векторное произведение, которое
можно преобразовать, используя
правило:

22. Электромагнитные волны

Получим уравнения:
1 2 E
1 2 B Волновое уравнение ЭМВ
E 2 2 B 2 2
произвольного направления
t
t
1
c
- фазовая скорость
0 0
м
c
3 10
с
0 0
1
8
1 2 f
Уравнение вида: f
2
2
t
f f ( x, y, z)
- Электродинамическая постоянная,
совпадает со скоростью ЭМВ в вакууме
называется волновым уравнением
- уравнение волны или волновая функция

23. Электромагнитные волны

2Ey
x
2
2H z
x
2
0 0
0 0
2Ey
t 2
2H z
t 2

24. Электромагнитные волны

Простейшее решение этих уравнений:
E y Em cos( t kx ) Em cos( (t ) )
H z H m cos( t kx )
x
Волны такого вида называются плоскими монохроматическими или
гармоническими.
Em ( H m ) - амплитуда волны,
Ф ( t kx )
x
- фаза волны, α - начальная фаза,
координата поверхности постоянной фазы, Ф=const в момент t,
υ - фазовая скорость волны,
2 2 / T - циклическая частота колебаний в волне,
- частота , Гц,
T - период колебаний,
k / - волновое число или постоянная распространения
1/ T

25. Электромагнитные волны

Обычно под волной понимают распространение колебаний в
пространстве. В общем случае волна – это распространение в пространстве
любого возмущения среды или поля ( акустические, механические, ЭМВ).
Особенностью волновых процессов является перенос энергии в
волне без переноса вещества.
По форме различают : 1) одиночные или импульсные волны, 2) цуг волны
или обрывок синусоиды, 3) гармонические или монохроматические волны,
представляющие собой бесконечную синусоиду.
В зависимости от направления колебаний в волне различают 1)
продольные и 2) поперечные волны. В продольных волнах частицы среды
совершают колебания в направлении распространения волны ( звук в газе),
в поперечных – в направлении перпендикулярном распространению ( чисто
поперечная ЭМВ).
Волны различают по типу волновой поверхности: плоские, сферические,
цилиндрические волны.
Волновая поверхность – это геометрическое место точек, колеблющихся в
одинаковой фазе. Волновой фронт – геометрическое место точек, до
которых доходят колебания в момент времени t.

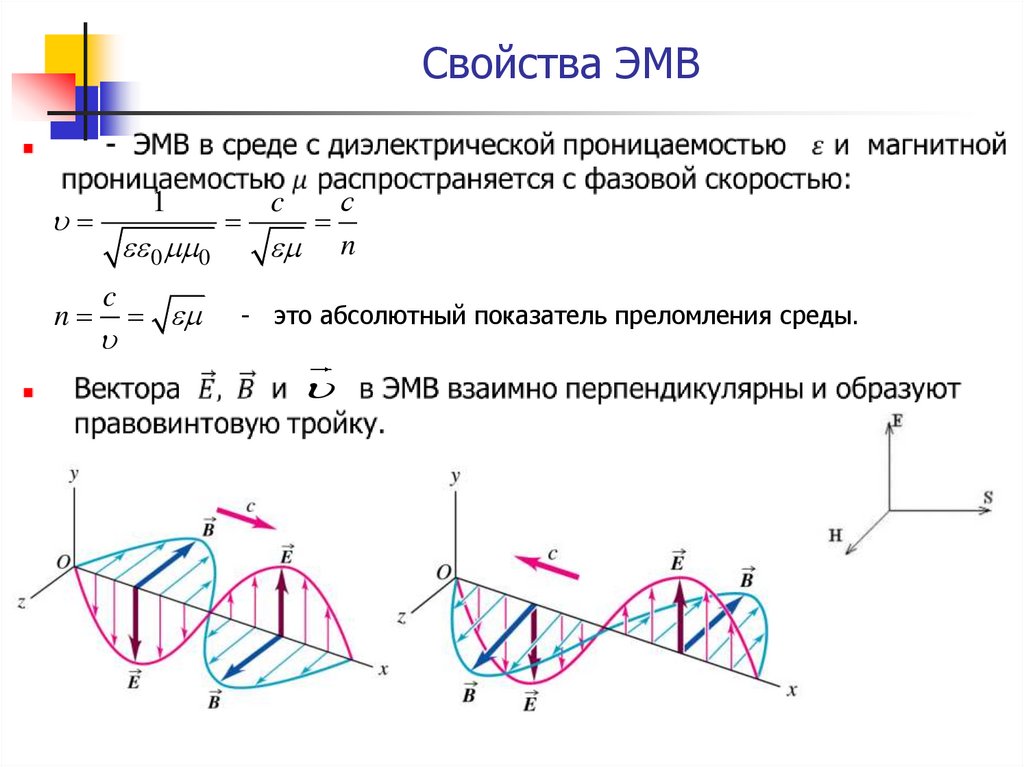
26. Свойства ЭМВ

1
n
0 0
c
c
с
n
- это абсолютный показатель преломления среды.

27. Свойства ЭМВ

В ЭМВ мгновенные значения векторов E и B всегда колеблются в
одинаковых фазах, причем между мгновенными значениями E и B в любой
точке существует определенная связь, а именно E v B , или
E B
1
0 0
B 0 H
0 E 0 H
Это значит, что Е и Н (или В) одновременно
достигают максимума, одновременно обращаются
в нуль , то есть колеблются синфазно.
Em Bm 0 Em 0 H m
ЭМВ обладают объемной плотностью энергии, мгновенное значение
которой равно:
0 E 2 0 H 2
EH
2
2
w wэл wмаг
0 E 0 H
2
2

28. Свойства ЭМВ

E Em cos t H H m cos t
2
2
E
H
1
cos2 t sin 2 t E 2 m , H 2 m
2
2
2
w 0 E 2
0 Em2
2
0 H m2
2
Em H m
2
W w V
Дж
S w 0 E 0 H E H 2
м с
2
2
S w E H

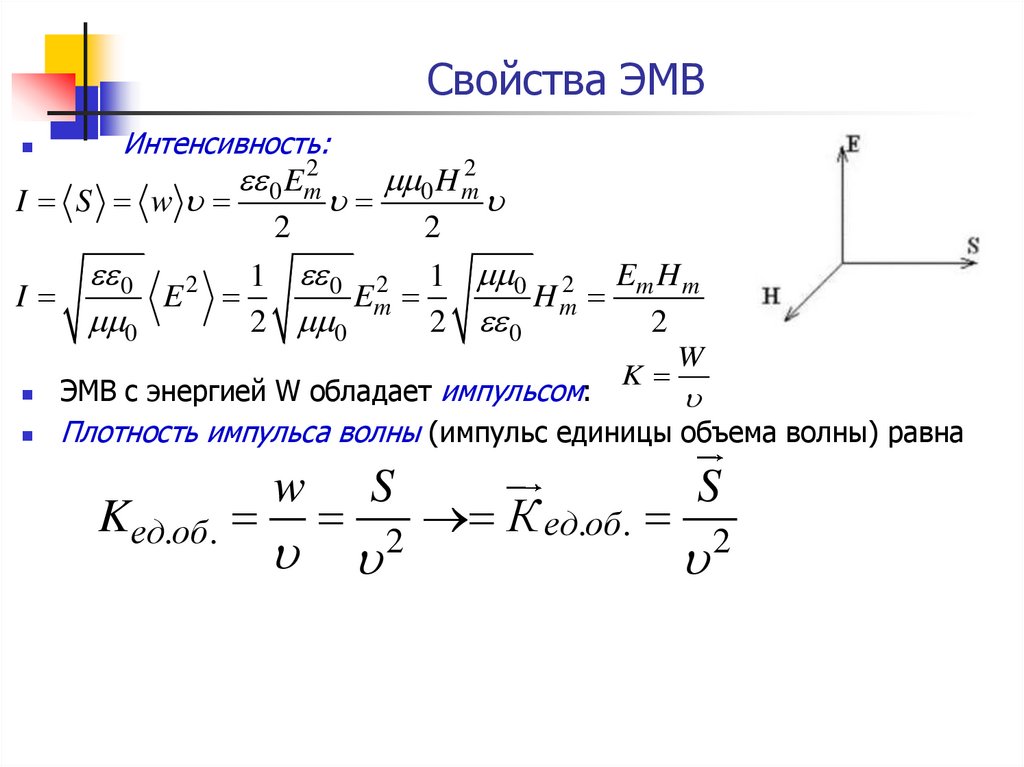
29. Свойства ЭМВ

Интенсивность:
I S w
I
0 Em2
2
0 H m2
2
0
1 0 2 1 0 2 Em H m
Hm
Em
E2
2
2 0
2 0
0
K
W
ЭМВ с энергией W обладает импульсом:
Плотность импульса волны (импульс единицы объема волны) равна
Kед.об.
w
S
2
К ед.об.
S
2

30. Диапазоны электромагнитных волн

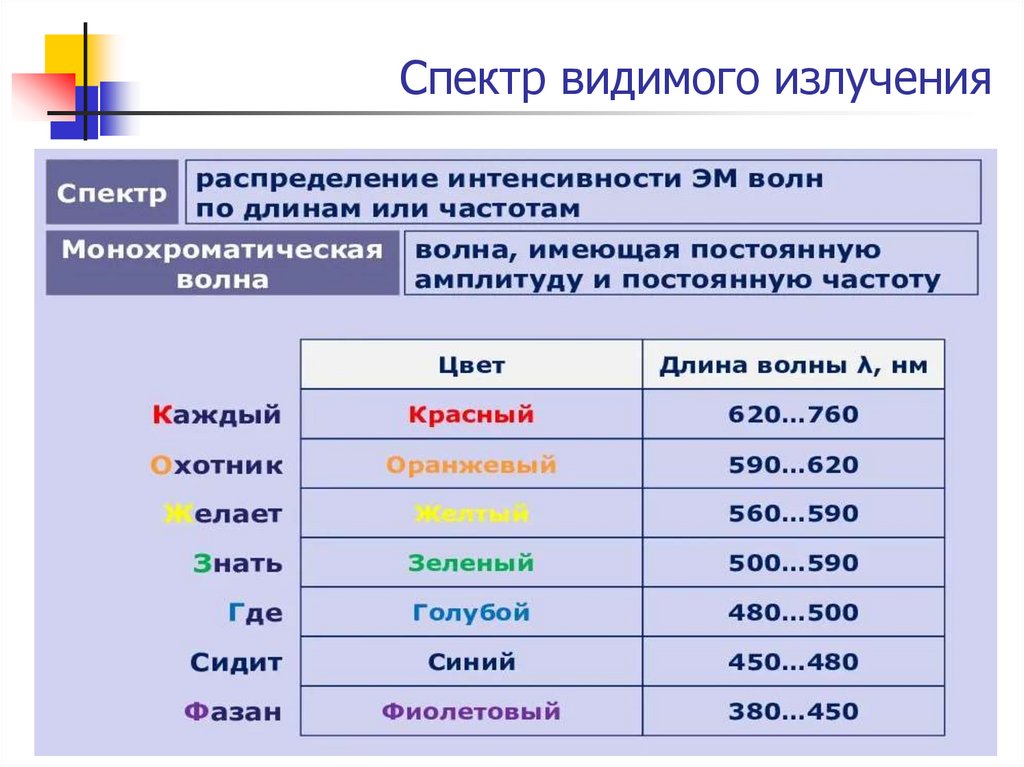
31. Спектр видимого излучения

32. Система уравнений Максвелла

33. Симметрия уравнений Максвелла

Уравнения Максвелла выполняются во всех инерциальных
системах отсчета. Они являются релятивистски инвариантными. Это
есть следствие принципа относительности, согласно которому все
инерциальные системы отсчета физически эквивалентны друг другу.
Факт инвариантности уравнений Максвелла (относительно
преобразований Лоренца) подтверждается многочисленными
опытными данными.
Уравнения Максвелла не симметричны относительно электрического
и магнитного полей. Это обусловлено тем, что в природе существуют
электрические заряды, но нет зарядов магнитных. Вместе с тем в
нейтральной однородной непроводящей среде, уравнения Максвелла
приобретают симметричный вид
E B / t
D 0
H D / t
B 0