Уравнения Максвелла. Вихревое электрическое поле

1. УРАВНЕНИЯ МАКСВЕЛЛА

2. 1. ВИХРЕВОЕ ЭЛЕКТРИЧЕСКОЕ ПОЛЕ

Если неподвижный проводящий контур
пронизывается переменным магнитным полем,
то в контуре появляется индукционный ток.
Возникновение индукционного тока говорит о
том, что изменение магнитного поля вызывает
появление в контуре сторонних сил F * qE * ,
действующих на носители тока (заряды).
Действие сторонней силы связано с появлением
вихревого электрического поля E * .
*
ЭДС индукции равна циркуляции E по контуру:
A* 1
i q q
1
*
F
dl
qE
dl
q
*
*
E
dl .

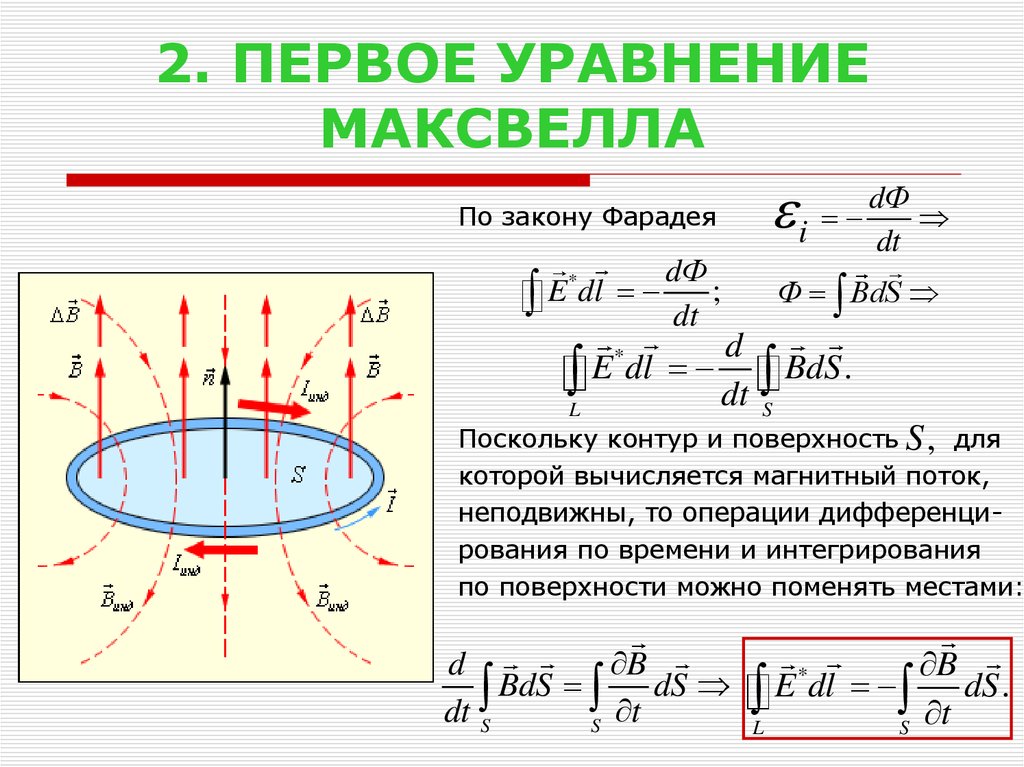
3. 2. ПЕРВОЕ УРАВНЕНИЕ МАКСВЕЛЛА

По закону Фарадея
dФ
E dl dt ;
Ф BdS
*
d
L E dl dt
*
dФ
i dt
BdS .
S
Поскольку контур и поверхность S , для
которой вычисляется магнитный поток,
неподвижны, то операции дифференцирования по времени и интегрирования
по поверхности можно поменять местами:
d
B
BdS dS
dt S
t
S
B
L E dl S t dS .
*

4. 3. ЗАКОН ФАРАДЕЯ В ДИФФЕРЕНЦИАЛЬНОЙ ФОРМЕ

Первое уравнение Максвелла выражает закон
электромагнитной индукции Фарадея:
B
L E dl S t dS .
*
Преобразуем левую часть по теореме Стокса:
*
*
dS
E
dl
E
L
S
B
*
S E dS S t dS .
Ввиду произвольности выбора поверхности
интегрирования в каждой точке должно
выполняться равенство
B
*
E ,
t
выражающее закон электромагнитной индукции Фарадея в дифференциальной форме.

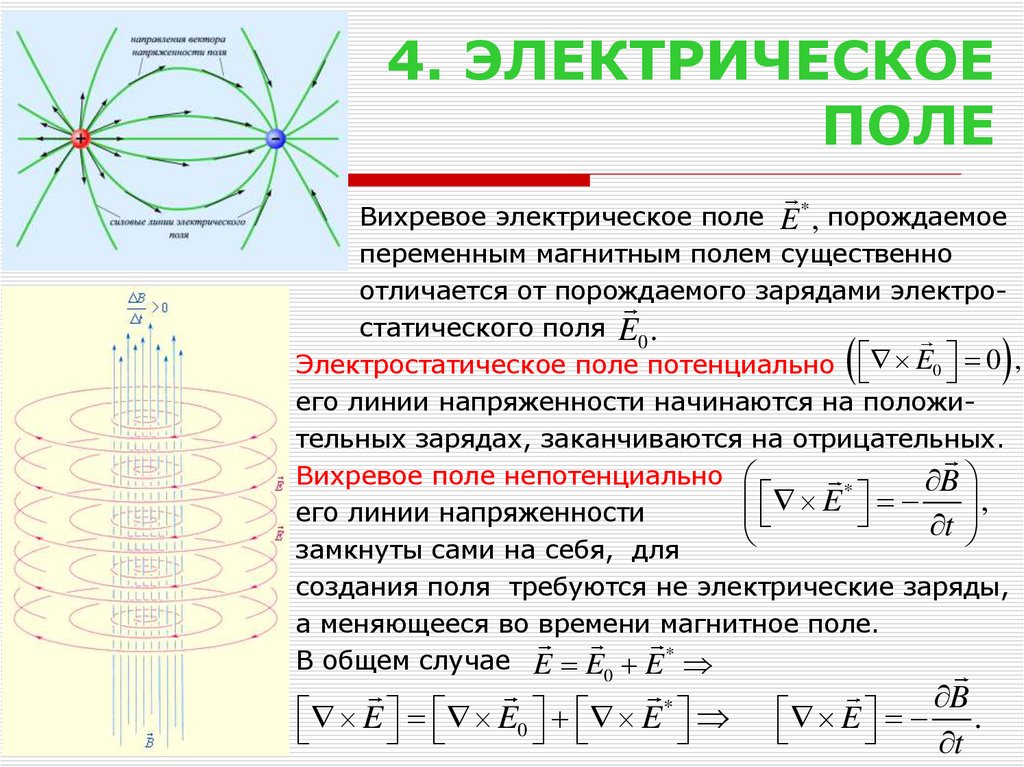
5. 4. ЭЛЕКТРИЧЕСКОЕ ПОЛЕ

Вихревое электрическое поле E * , порождаемое
переменным магнитным полем существенно
отличается от порождаемого зарядами электростатического поля E0 .
Электростатическое поле потенциально E0 0 ,
его линии напряженности начинаются на положительных зарядах, заканчиваются на отрицательных.
Вихревое поле непотенциально
B
*
E ,
его линии напряженности
t
замкнуты сами на себя, для
создания поля требуются не электрические заряды,
а меняющееся во времени магнитное поле.
В общем случае E E0 E *
E E0 E *
B
E .
t

6. 5. УРАВНЕНИЕ НЕПРЕРЫВНОСТИ

Рассмотрим воображаемую замкнутую поверхность S в некоторой среде с током.
Выражение
jdS определяет заряд, вышедший из объема
V,
S
ограниченного поверхностью S .
В силу закона сохранения заряда эта величина должна быть равна
скорости убывания заряда q , содержащегося в данном объеме:
S
dq
jdS ;
q dV
dt
V
d
dV
dV
dt V
t
V
По теореме Остроградского-Гаусса
j
dV
dV
j
V
V t
t
S
d
S jdS dt V dV ;
jdS
dV .
t
V
jdS j dV
S
V
- уравнение
непрерывности.
const j 0.

7. 6. ТОК СМЕЩЕНИЯ

Теорема о циркуляции в виде H j
противоречит уравнению непрерывности:
H j ;
H 0
j 0,
но
j
.
t
Вывод: j 0 только для стационарных процессов, при нестационарных
процессах плотность зарядов может меняться со временем. В этом
случае в полном согласии с уравнением непрерывности j 0.
Чтобы согласовать теорему о циркуляции и уравнение непрерывности,
Максвелл ввел в правую часть теоремы о циркуляции дополнительное
слагаемое и назвал его плотностью тока смещения. Таким образом,
H j0 jc ;
j0 j ;
jп j jc . jc D H j D .
t
t
Сумму тока проводимости и тока смещения принято называть полным
током.

8. 7. УРАВНЕНИЯ МАКСВЕЛЛА В ИНТЕГРАЛЬНОЙ ФОРМЕ

9. 8. УРАВНЕНИЯ МАКСВЕЛЛА В ДИФФЕРЕНЦИАЛЬНОЙ ФОРМЕ