Функции y = tgx и y = ctgx, их свойства и графики

1.

Функции y = tgx и
y = ctgx,
их свойства и
графики

2.

10.02.2022г.
Задание высылать не позднее
16:00 10.02.2022г в личном
сообщении в вк или на почту
[email protected]
Перед каждым заданием в
тетради пишем ФИО, дата, тема
урока

3.

Определение
Тангенсом угла α называют число, равное
отношению sin α к cos α, обозначают tg α, т. е.
sin
tg
cos
2
k , k Z
Тангенс определён для всех углов α, кроме тех,
для которых косинус равен нулю
Для любого угла α ≠ π/2 + πk, kЄZ существует, и притом
единственный tg α

4.

Ось тангенсов
tg
tg
3
3
4
+∞
y
120°
2
3
3
4
1
tg 45 1
tg120 3
1
6
180°
tg180 0
tg90 не существует
Тангенс может
принимать любые
значения от – ∞ до + ∞
1
3
3
0
x
6
- 45° 3
3
3
4
1
2
3
х=1
–∞

5.

Определение
Котангенсом угла α называют число, равное
отношению cos α к sin α, обозначают сtg α, т. е.
cos
сtg
sin
k , k Z
Котангенс определён для всех углов α, кроме тех,
для которых синус равен нулю
Для любого угла α ≠ πk, kЄZ существует, и притом
единственный сtg α

6.

Y
Ось котангенсов
сtg
сtg
3
4
–∞
1
3
3
1
3
3
0
120°
180°
3
3
3
+∞
1
у=1
4
0°
сtg 45 1
45°
3
сtg120 3
сtg180 Не существует
Котангенс может
принимать любые
значения от – ∞ до + ∞
X
сtg ( 90 ) 0

7.

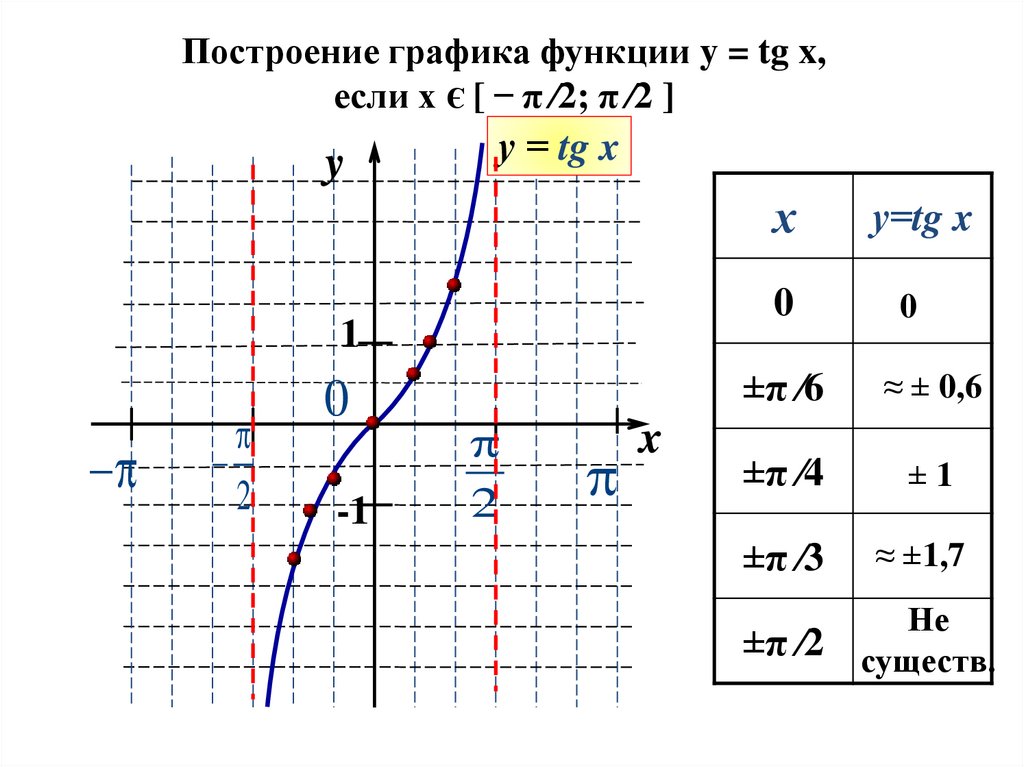
Построение графика функции y = tg x,
если х Є [ ̶ π ∕2; π ∕2 ]
y
у = tg x
х
0
1
2
0
-1
2
x
у=tg x
0
±π ∕6
≈ ± 0,6
±π ∕4
±1
±π ∕3
≈ ±1,7
±π ∕2
Не
существ.

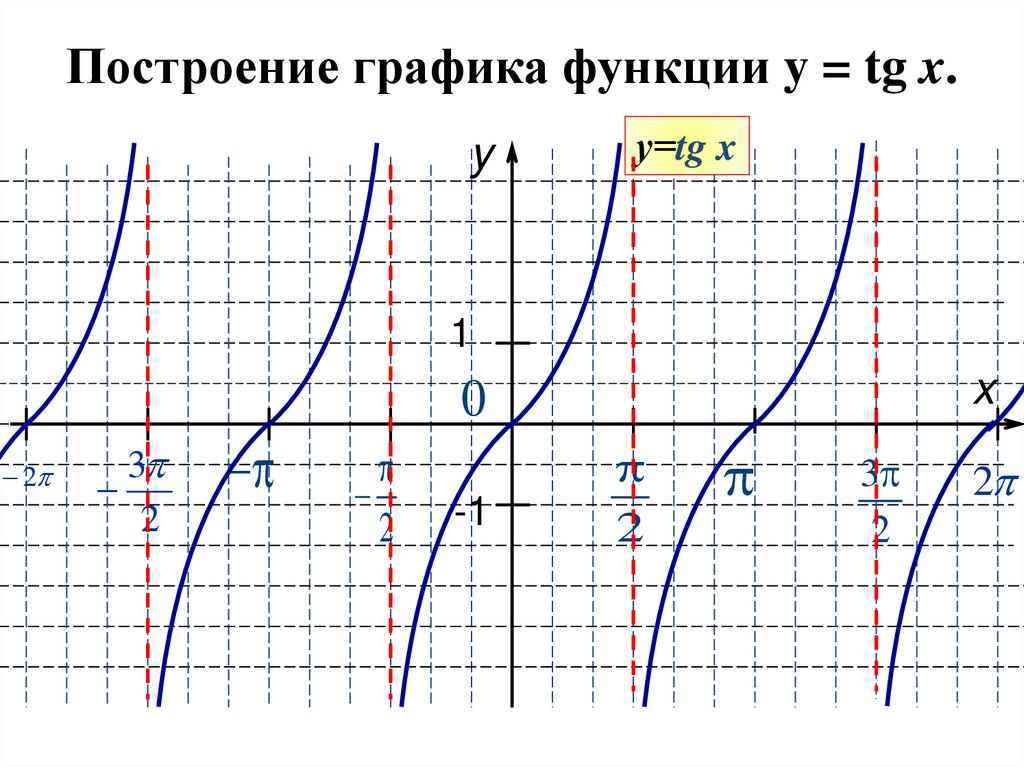
8. Построение графика функции y = tg x.

y
у=tg x
1
x
0
2
3
2
2
-1
2
3
2
2

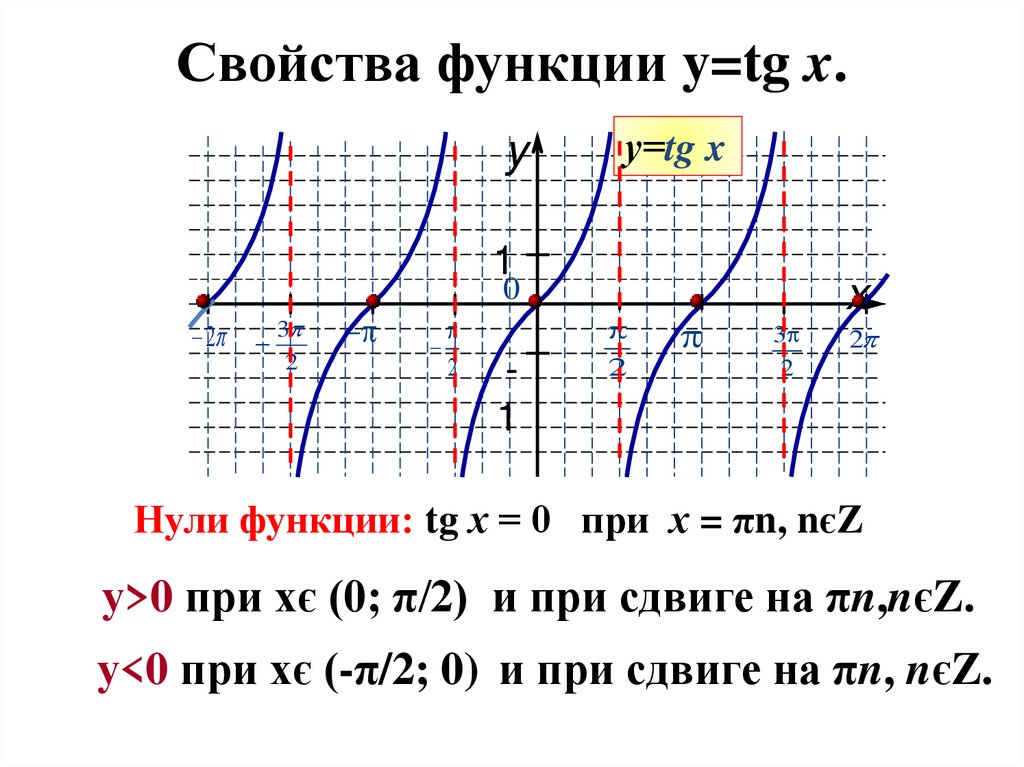
9. Свойства функции y=tg x.

y
у=tg x
1
0
2
3
2
2
1
2
3
2
x
2
Нули функции: tg х = 0 при х = πn, nєZ
у>0 при хє (0; π/2) и при сдвиге на πn,nєZ.
у<0 при хє (-π/2; 0) и при сдвиге на πn, nєZ.

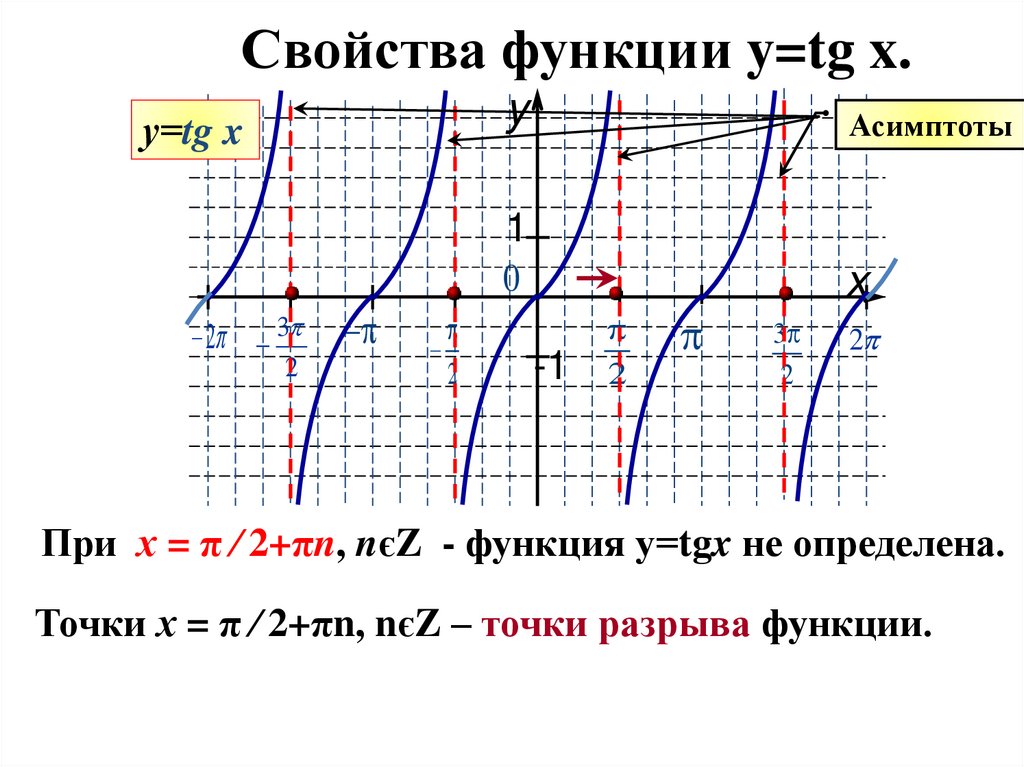
10. Свойства функции y=tg x.

у=tg x
2
3
2
2
y
Асимптоты
1
0
x
-1
2
3
2
2
При х = π ∕ 2+πn, nєZ - функция у=tgx не определена.
Точки х = π ∕ 2+πn, nєZ – точки разрыва функции.

11. Запишите все свойства функции y = tg x.

1. Обл. определения:
2. Множество значений функции: уєR
3. Периодическая, Т= π
4. Нечётная функция
5. Возрастает на всей области определения
6. Выпукла вниз при
[Пn; П/2+ Пn),
выпукла вверх при
(-П/2+Пn; Пn],
7.Не ограничена
8. У наиб- не существует, у наим -не существует
9. При х = π ∕ 2+πn, nєZ -имеет точки разрыва графика и
асимптоты

12.

у
1
х
- 2
-
3
2
y = tgx + a
-
-
2
0
-1
y = tgx
2
3
2
y = tgx – b
2

13.

у
1
х
- 2
-
3
2
-
y = tgx
-
2
0
-1
2
y = tg(x – a)
3
2
2

14.

у
1
х
- 2
-
3
2
-
y = tgx
-
2
0
-1
2
3
2
y = ItgxI
2

15.

Функция y = ctg x
1.
2.
3.
Область значений функции
– все действительные
числа.
Функция убывает на
интервалах
k ; k ,k Z
4.
5.
у=ctg x
Область определения
данной функции – все
действительные числа,
кроме чисел х=πk, k Z.
Функция нечетная, график
ее симметричен
относительно начала
координат.
Функция периодическая,
ее наименьший
положительный период
равен π.
у
1
- 3
2
-π
-
0
2
-1
2
π
3
2
х

16. Задача №1.

Найти все корни уравнения tgx = 1,
принадлежащих промежутку –π ≤ х ≤ 3π ∕ 2.
Решение.
1. Построим графики
у=tg x
y
у=1
−π
1
х1
0
1
х2
функций у=tgx и у=1
2. х1= − 3π∕4
х2= π∕4
x
х3= 5π∕4
х
3π/2
3
π

17.

Задача №2.
Найти все решения неравенства tgx < − 1,
принадлежащие промежутку –π ≤ х ≤ 2π .
1. Построим графики функций у = tgx и у = −1
у=tg x
y
(
−π/4
2
//////
1
3π/4
0
//////
2
-1
7π/4
)
3 ////////
2
2
2. хϵ(−π/2; −π∕4); хϵ(π/2; 3π∕4); хϵ(3π/2; 7π∕4)
x
у = −1