Похожие презентации:
Функции y = tgx и y = ctgx, их свойства и графики
1.
Функции y = tgx иy = ctgx,
их свойства и
графики
2.
ОпределениеТангенсом угла α называют число, равное
отношению sin α к cos α, обозначают tg α, т. е.
sin
tg
k , k Z
cos
2
Тангенс определён для всех углов α, кроме тех,
для которых косинус равен нулю
Для любого угла α ≠ π/2 + πk, kЄZ существует, и притом
единственный tg α
3.
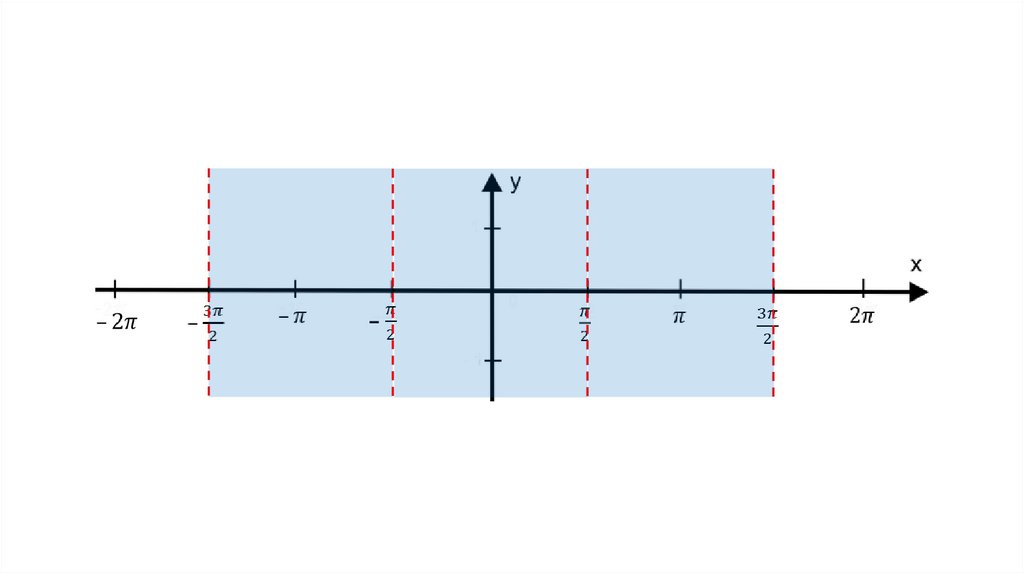
у = tg x;4.
5.
у = tg x;Свойство 2. Функция у = tg x является периодической с
основным периодом π.
tg(x– π) = tg x = tg(x+π);
6.
Для любого допустимого значения t справедливы равенства:tg (t + π)= tg t
ctg (t + π) = ctg t
7.
у = tg x;Свойство 3. Функция у = tg x является нечетной
функцией, так как справедливо равенство tg (–x) = – tg x.
8.
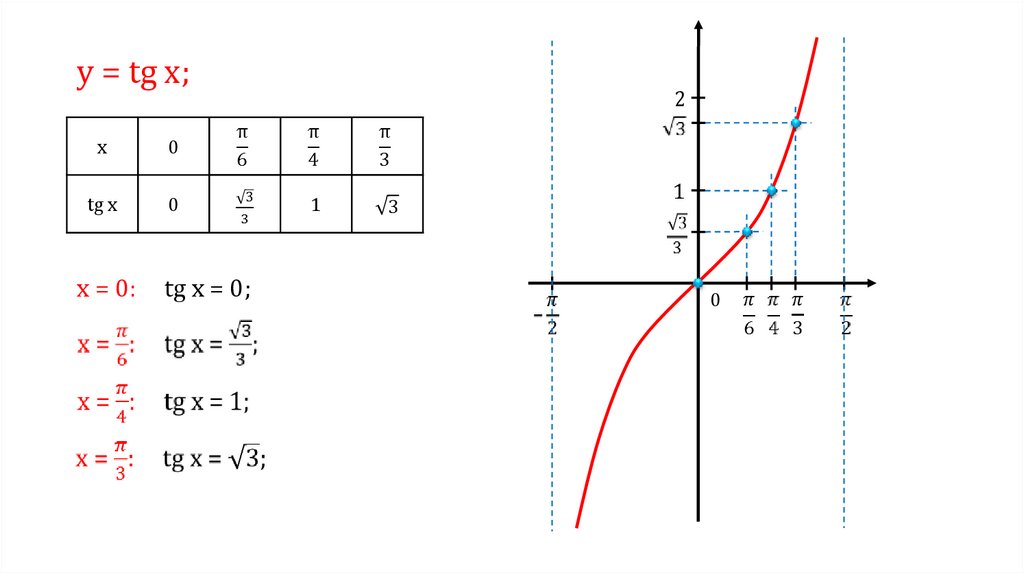
у = tg x;x
0
tg x
0
х = 0:
tg x = 0;
2
1
1
0
9.
21
0
10.
у = tg x;11.
у = tg x;Свойство 5. Функция у = tg x не ограничена ни сверху, ни
снизу.
12.
у = tg x;Свойство 6. Функция у = tg x не имеет ни наибольшего,
ни наименьшего значений.
13.
у = tg x;14.
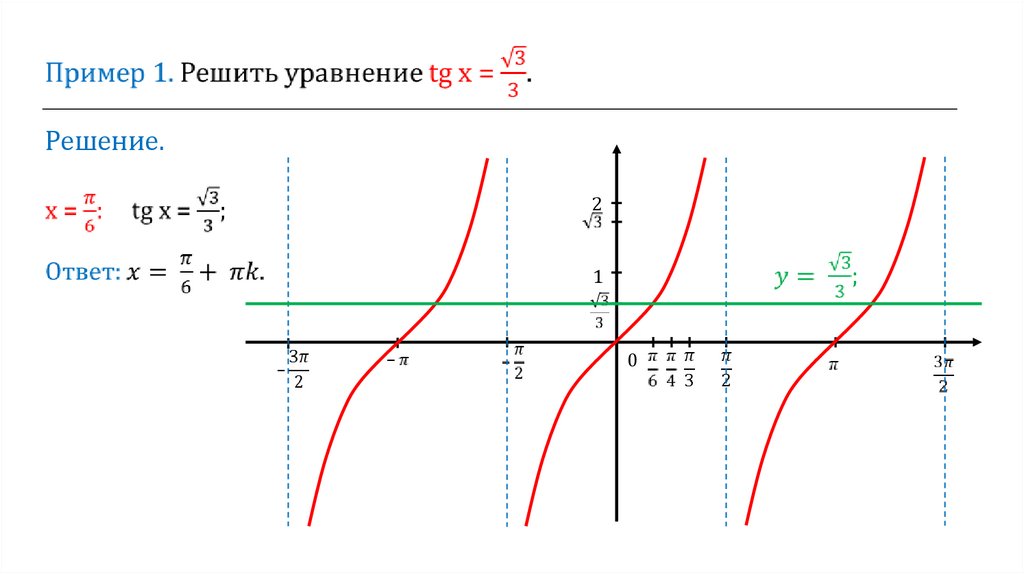
у = tg x;15.
Решение.2
1
0
16.
ОпределениеКотангенсом угла α называют число, равное
отношению cos α к sin α, обозначают сtg α, т. е.
cos
k , k Z
сtg
sin
Котангенс определён для всех углов α, кроме тех,
для которых синус равен нулю
Для любого угла α ≠ πk, kЄZ существует, и притом
единственный сtg α
17.
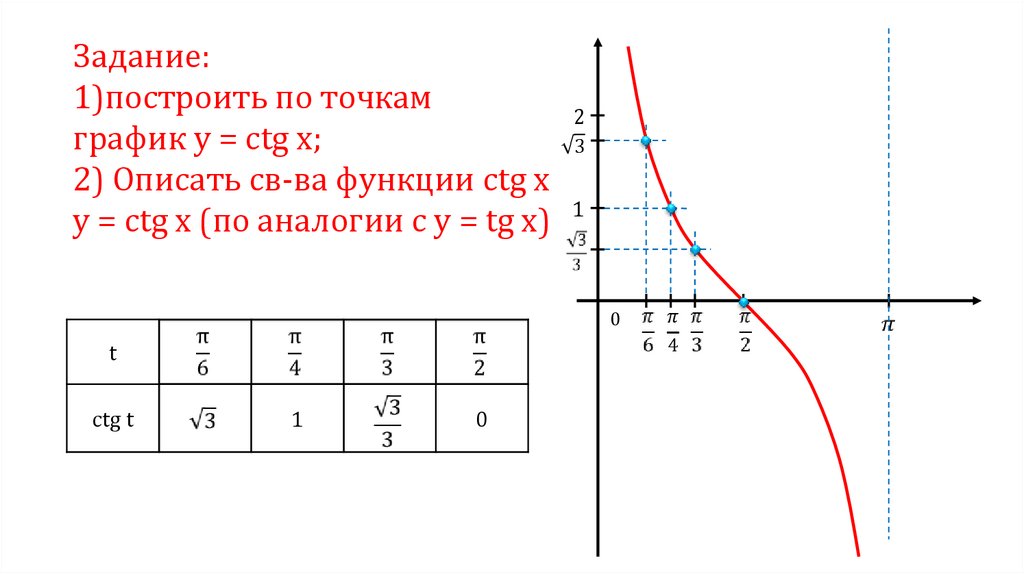
Задание:1)построить по точкам
2
график у = сtg x;
2) Описать св-ва функции сtg x
у = сtg x (по аналогии с у = tg x) 1
0
t
ctg t
1
0
18.
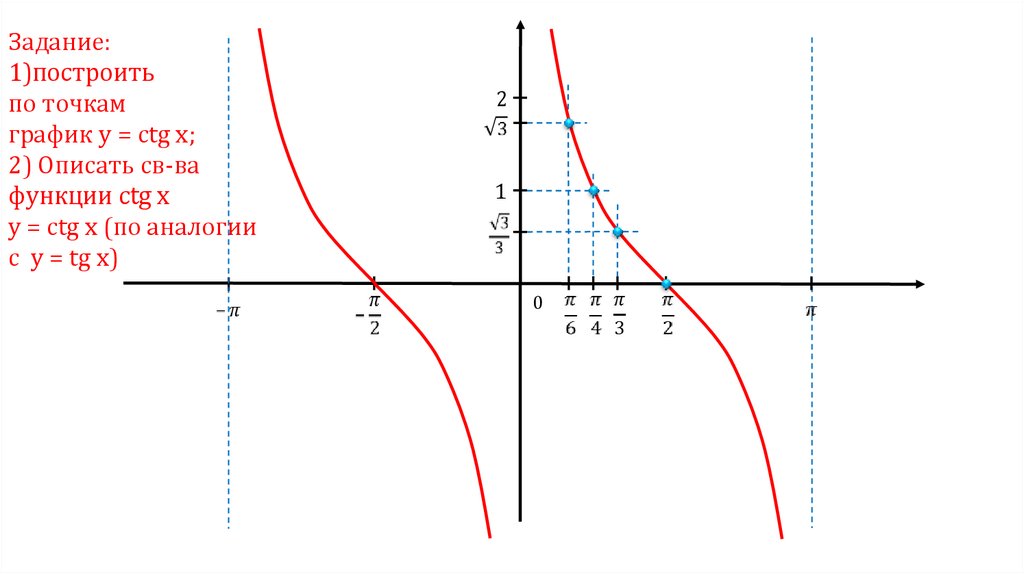
Задание:1)построить
по точкам
график у = сtg x;
2) Описать св-ва
функции сtg x
у = сtg x (по аналогии
с у = tg x)
2
1
0
19.
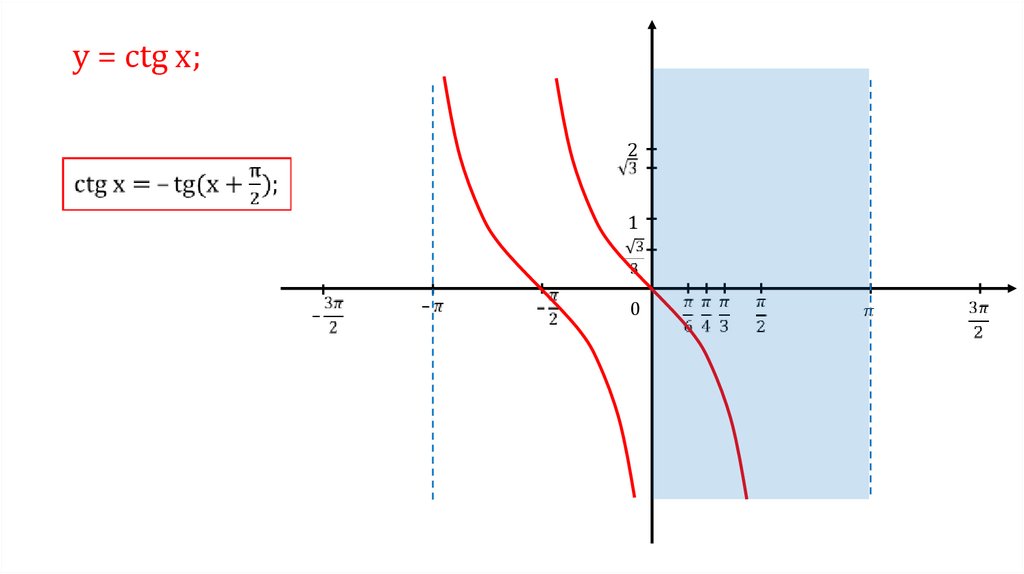
у = сtg x;2
1
0













 Математика
Математика