Современная модель пористости СКМ ЛП «Полигософт» и пути ее совершенствования

1. СОВРЕМЕННАЯ МОДЕЛЬ ПОРИСТОСТИ СКМ ЛП «ПОЛИГОСОФТ» И ПУТИ ЕЕ СОВЕРШЕНСТВОВАНИЯ

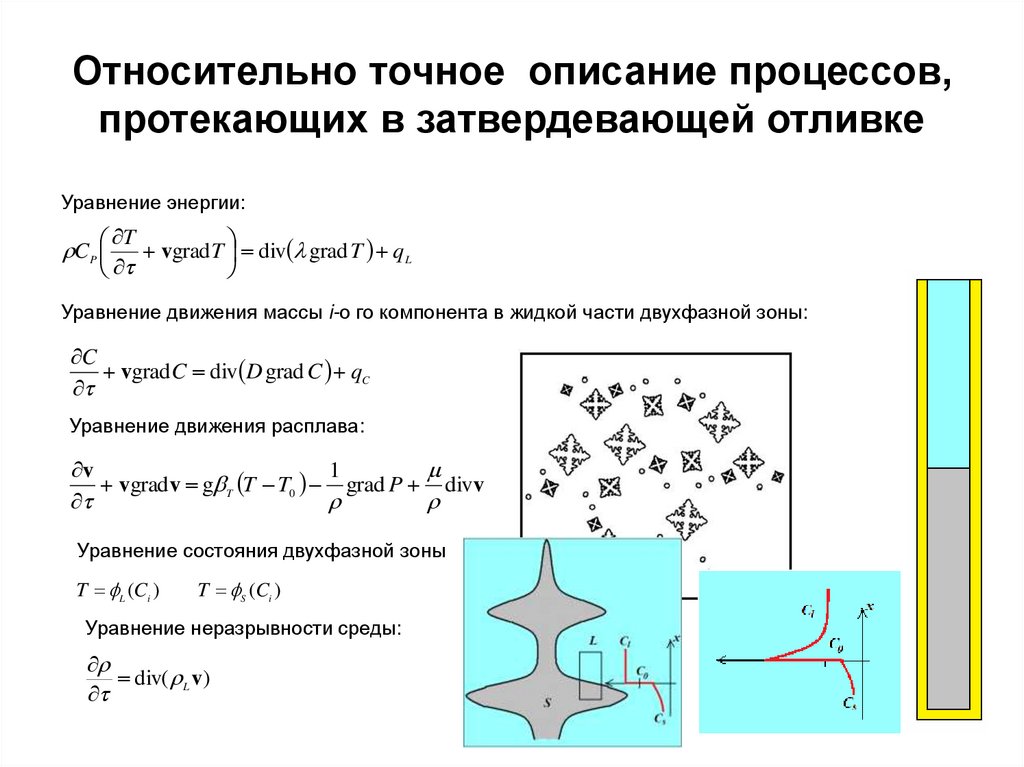
2. Относительно точное описание процессов, протекающих в затвердевающей отливке

Уравнение энергии:
T
vgradT div grad T q L
C P
Уравнение движения массы i-о го компонента в жидкой части двухфазной зоны:
C
vgradC div D grad C qC
Уравнение движения расплава:
v
1
vgradv g T T T0 grad P divv
Уравнение состояния двухфазной зоны
T L (Ci )
T S (Ci )
Уравнение неразрывности среды:
div( L v)

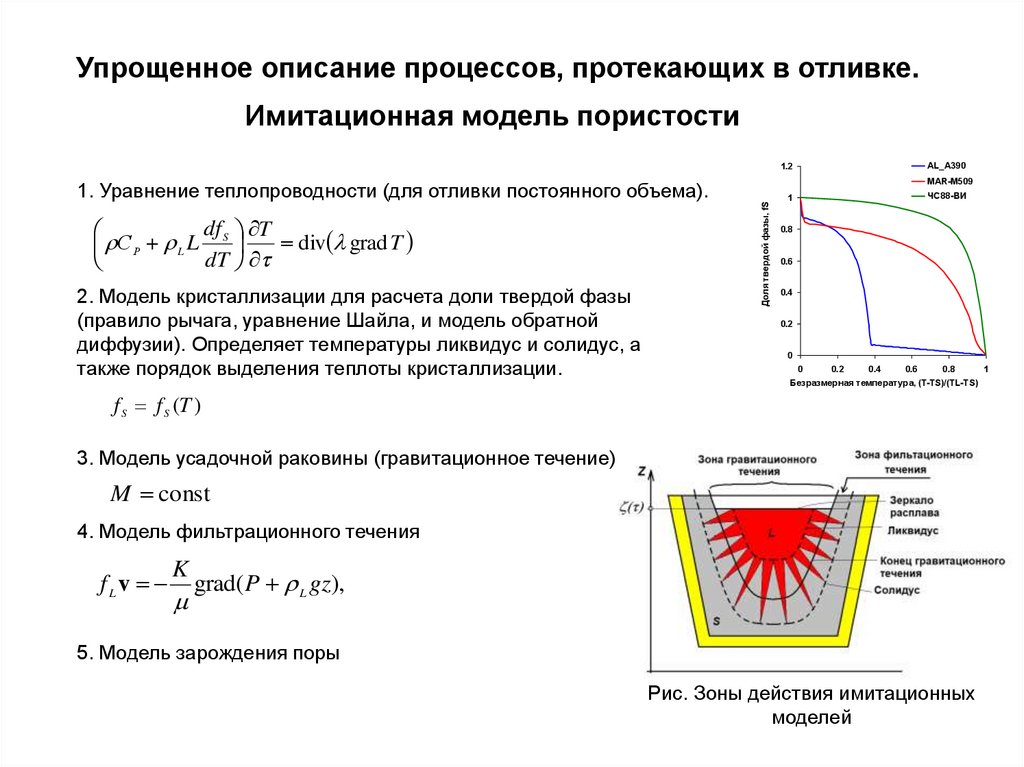
3. Упрощенное описание процессов, протекающих в отливке. Имитационная модель пористости

AL_A390
1.2
df T
div grad T
С Р L L S
dT
2. Модель кристаллизации для расчета доли твердой фазы
(правило рычага, уравнение Шайла, и модель обратной
диффузии). Определяет температуры ликвидус и солидус, а
также порядок выделения теплоты кристаллизации.
MAR-M509
Доля твердой фазы, fS
1. Уравнение теплопроводности (для отливки постоянного объема).
ЧС88-ВИ
1
0.8
0.6
0.4
0.2
0
0
0.2
0.4
0.6
0.8
Безразмерная температура, (T-TS)/(TL-TS)
f S f S (T )
3. Модель усадочной раковины (гравитационное течение)
M const
4. Модель фильтрационного течения
fLv
K
grad( P L gz),
5. Модель зарождения поры
Рис. Зоны действия имитационных
моделей
1

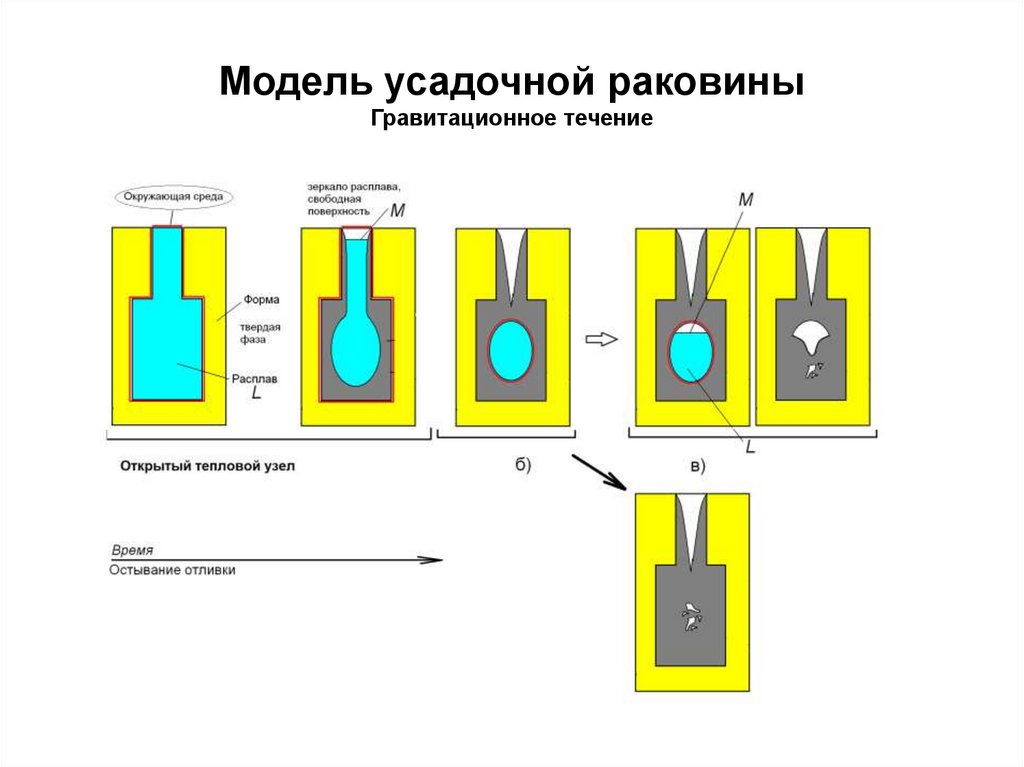
4. Модель усадочной раковины Гравитационное течение

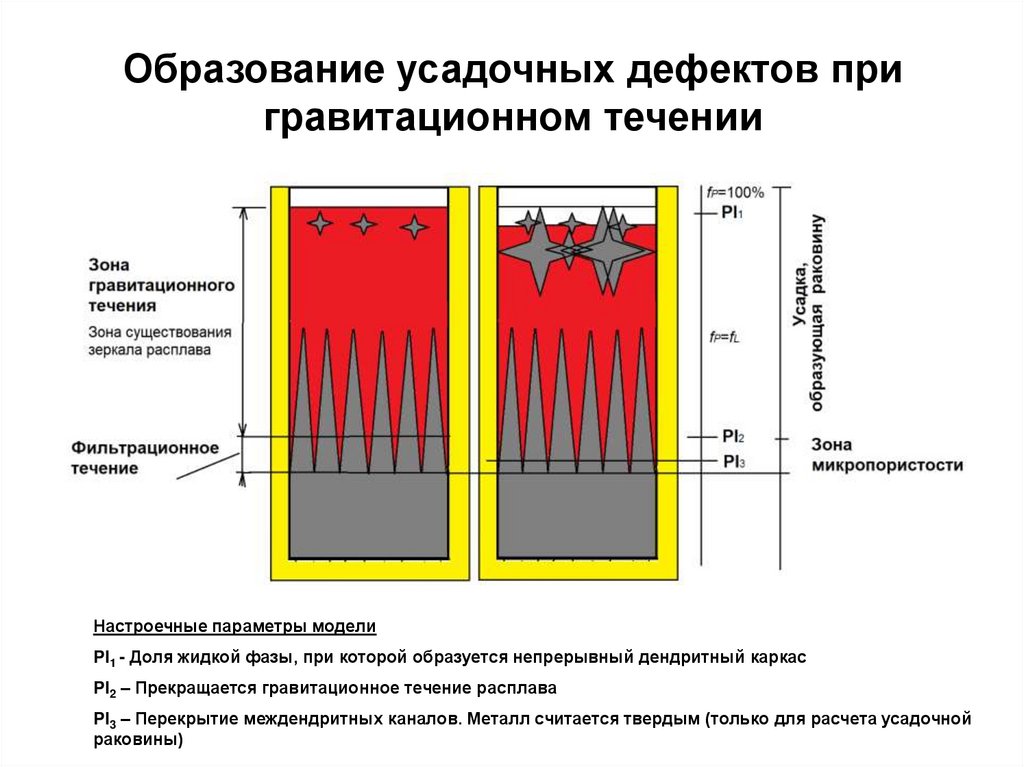
5. Образование усадочных дефектов при гравитационном течении

Настроечные параметры модели
Pl1 - Доля жидкой фазы, при которой образуется непрерывный дендритный каркас
Pl2 – Прекращается гравитационное течение расплава
Pl3 – Перекрытие междендритных каналов. Металл считается твердым (только для расчета усадочной
раковины)

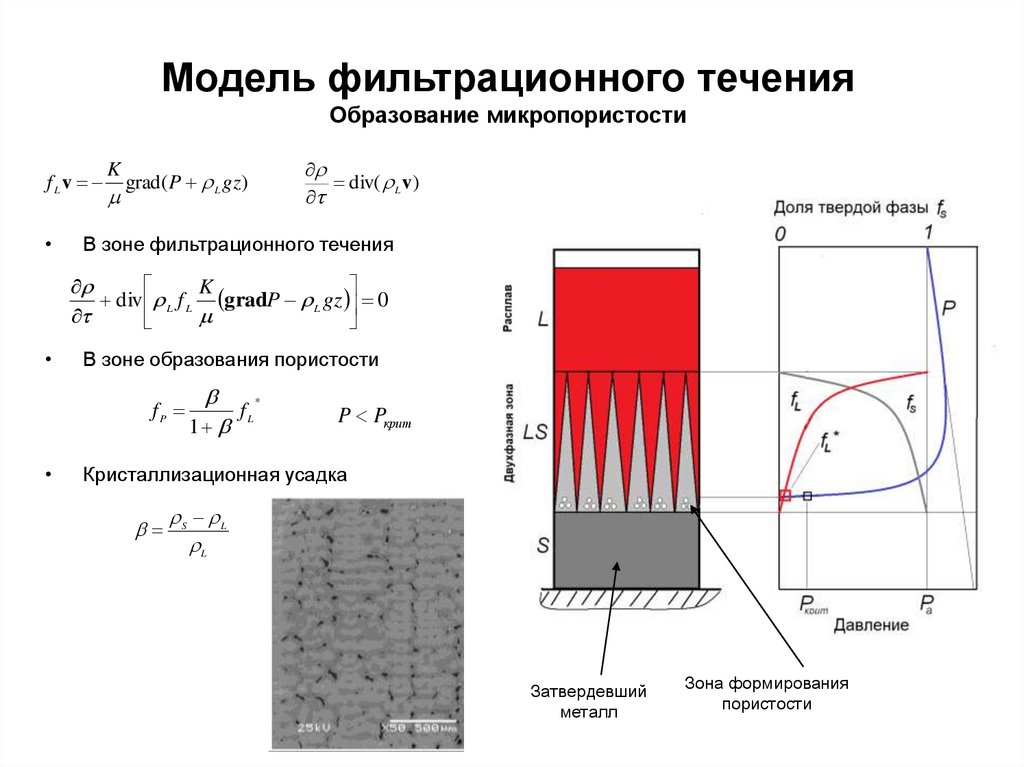
6. Модель фильтрационного течения Образование микропористости

fLv
K
div( L v)
grad( P L gz)
В зоне фильтрационного течения
K
div L f L gradP L gz 0
В зоне образования пористости
fP
1
fL
*
P Pкрит
Кристаллизационная усадка
S L
L
Затвердевший
металл
Зона формирования
пористости

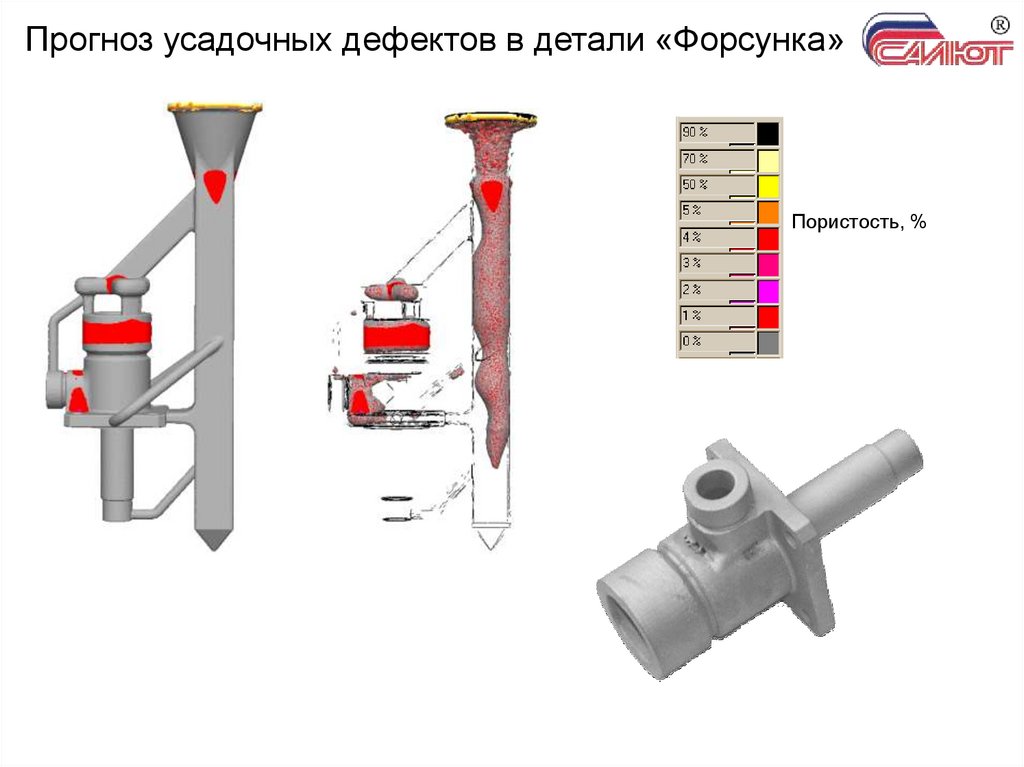
7. Прогноз усадочных дефектов в детали «Форсунка»

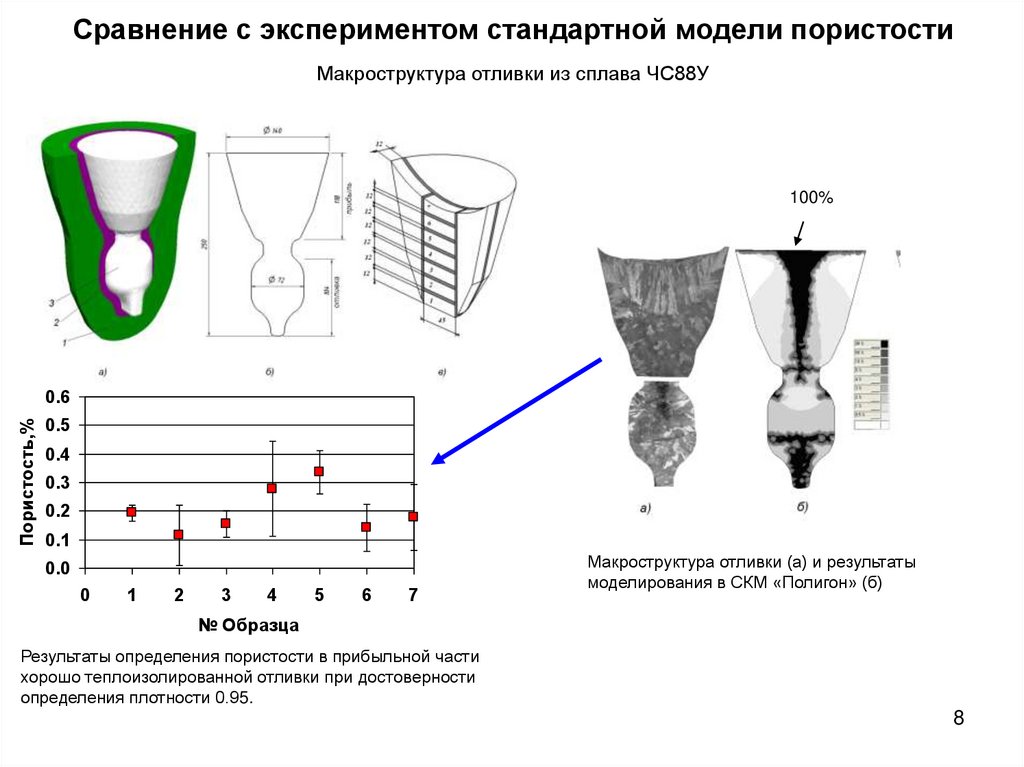
Пористость, %

8. Сравнение с экспериментом стандартной модели пористости Макроструктура отливки из сплава ЧС88У

100%
Пористость,%
0.6
0.5
0.4
0.3
0.2
0.1
0.0
0
1
2
3
4
5
6
7
Макроструктура отливки (а) и результаты
моделирования в СКМ «Полигон» (б)
№ Образца
Результаты определения пористости в прибыльной части
хорошо теплоизолированной отливки при достоверности
определения плотности 0.95.
8

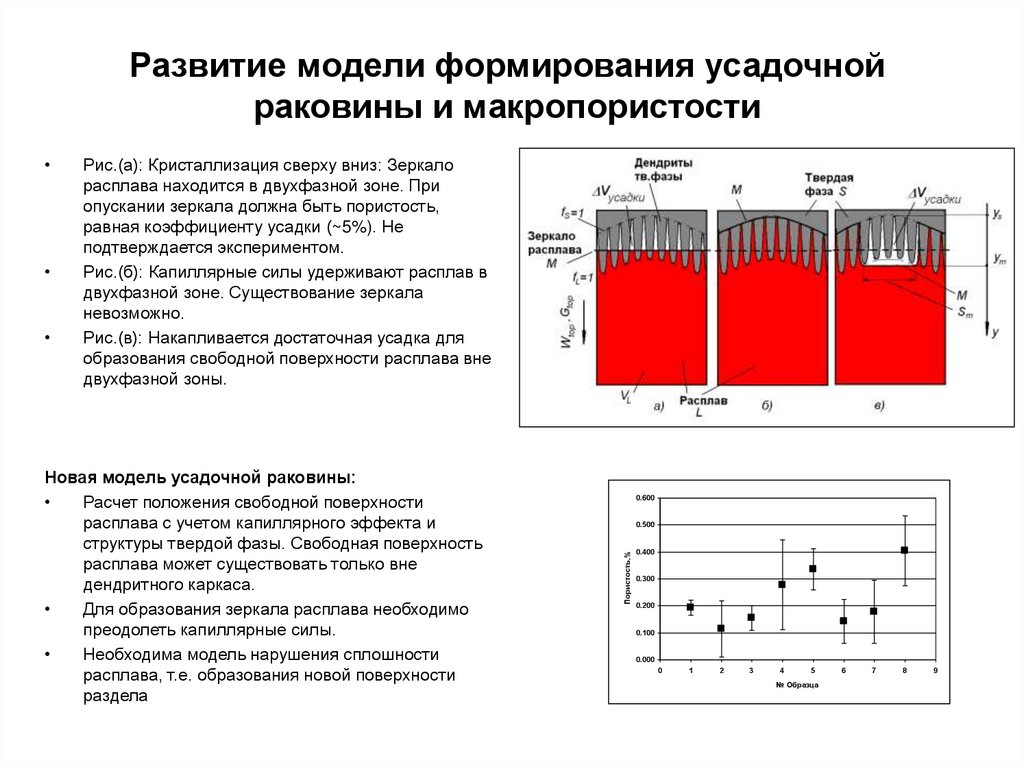
9. Развитие модели формирования усадочной раковины и макропористости

Рис.(а): Кристаллизация сверху вниз: Зеркало
расплава находится в двухфазной зоне. При
опускании зеркала должна быть пористость,
равная коэффициенту усадки (~5%). Не
подтверждается экспериментом.
Рис.(б): Капиллярные силы удерживают расплав в
двухфазной зоне. Существование зеркала
невозможно.
Рис.(в): Накапливается достаточная усадка для
образования свободной поверхности расплава вне
двухфазной зоны.
Новая модель усадочной раковины:
Расчет положения свободной поверхности
расплава с учетом капиллярного эффекта и
структуры твердой фазы. Свободная поверхность
расплава может существовать только вне
дендритного каркаса.
Для образования зеркала расплава необходимо
преодолеть капиллярные силы.
Необходима модель нарушения сплошности
расплава, т.е. образования новой поверхности
раздела
0.600
0.500
Пористость,%
0.400
0.300
0.200
0.100
0.000
0
1
2
3
4
5
№ Образца
6
7
8
9

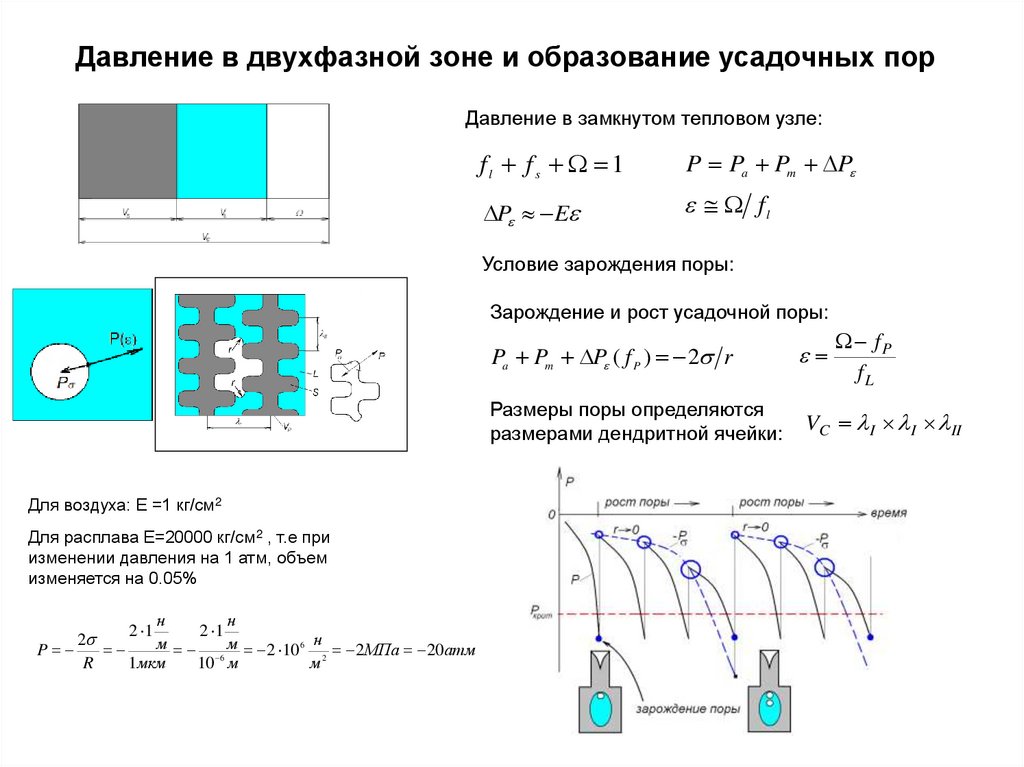
10. Давление в двухфазной зоне и образование усадочных пор

Давление в замкнутом тепловом узле:
fl f s 1
P Pa Pm P
P E
fl
Условие зарождения поры:
Зарождение и рост усадочной поры:
Pa Pm P ( f P ) 2 r
P Pкрит
Для воздуха: Е =1 кг/см2
Для расплава Е=20000 кг/см2 , т.е при
изменении давления на 1 атм, объем
изменяется на 0.05%
н
н
2 1
2
м
м 2 10 6 н 2 МПа 20 атм
P
6
R
1мкм
10 м
м2
2 1
Размеры поры определяются
размерами дендритной ячейки:
fP
fL
VC I I II

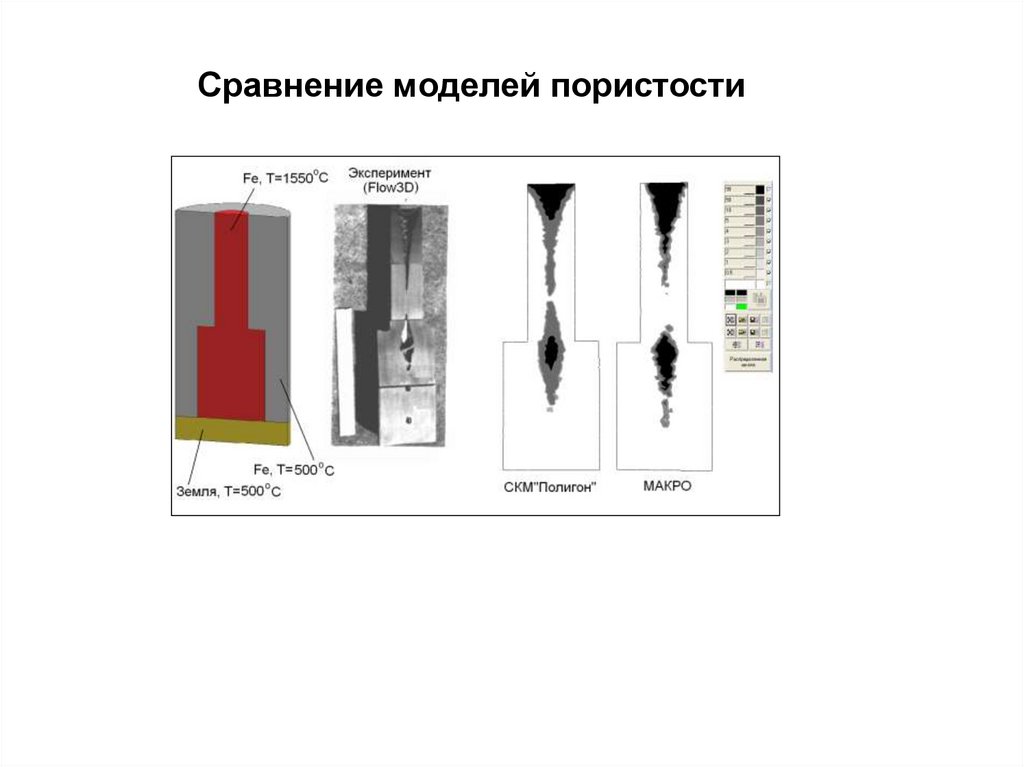
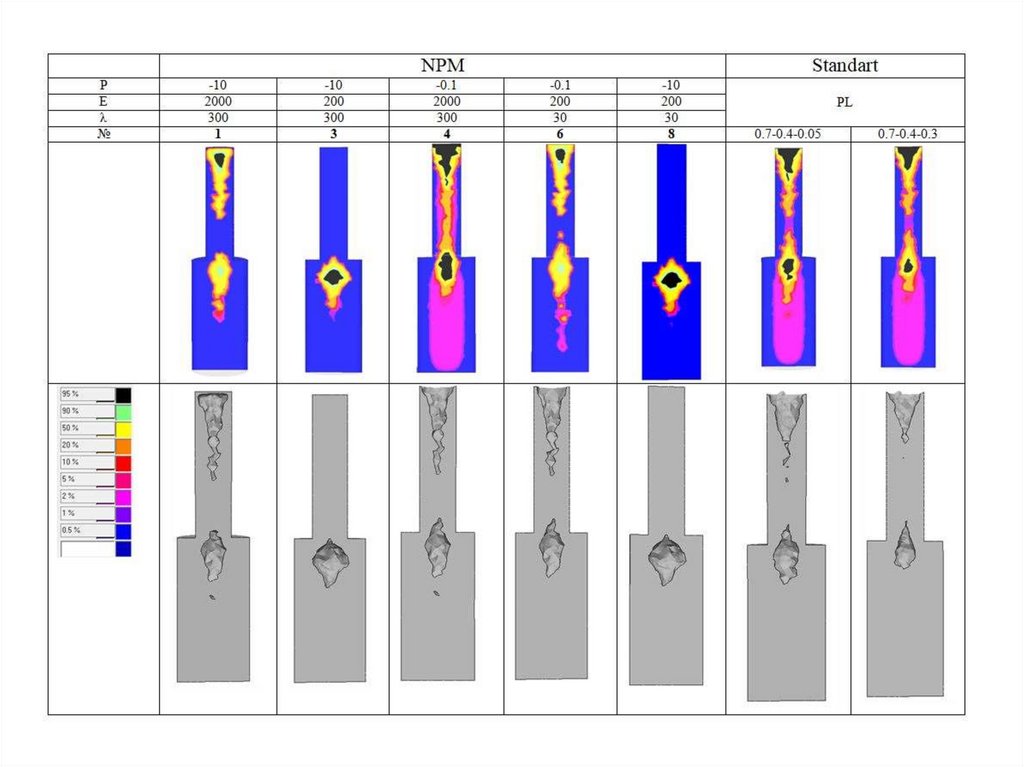
11. Сравнение моделей пористости

12.

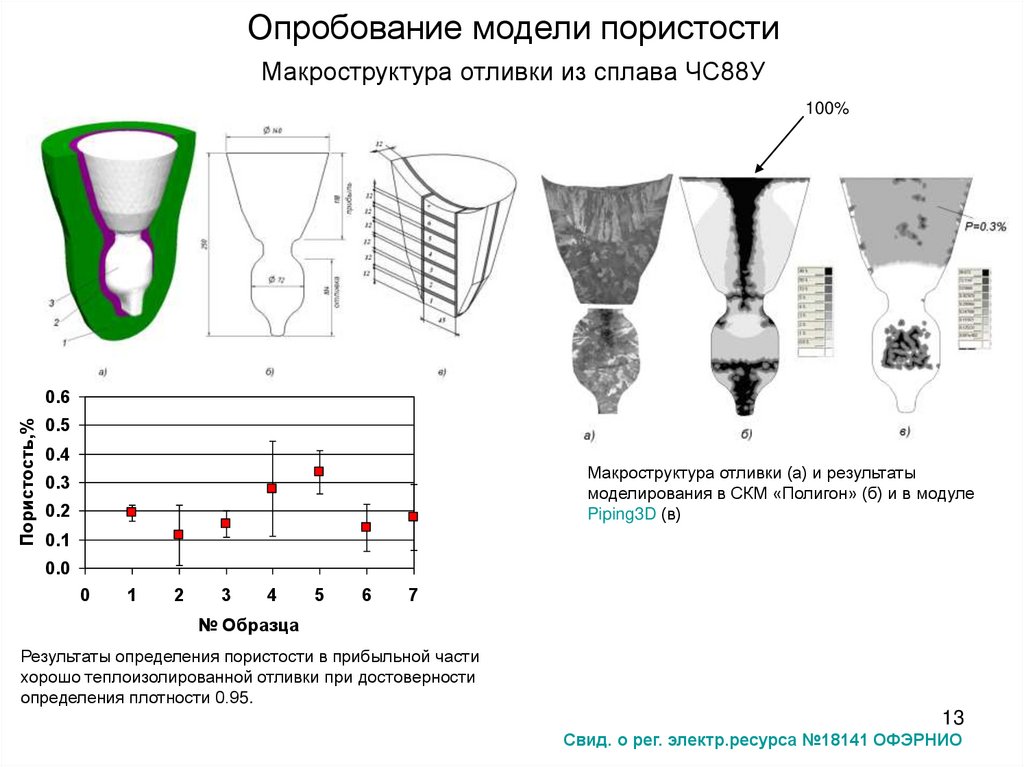
13. Опробование модели пористости Макроструктура отливки из сплава ЧС88У

100%
Пористость,%
0.6
0.5
0.4
Макроструктура отливки (а) и результаты
моделирования в СКМ «Полигон» (б) и в модуле
Piping3D (в)
0.3
0.2
0.1
0.0
0
1
2
3
4
5
6
7
№ Образца
Результаты определения пористости в прибыльной части
хорошо теплоизолированной отливки при достоверности
определения плотности 0.95.
13
Свид. о рег. электр.ресурса №18141 ОФЭРНИО

14. Экспериментальная проверка модей пористости Методика эксперимента

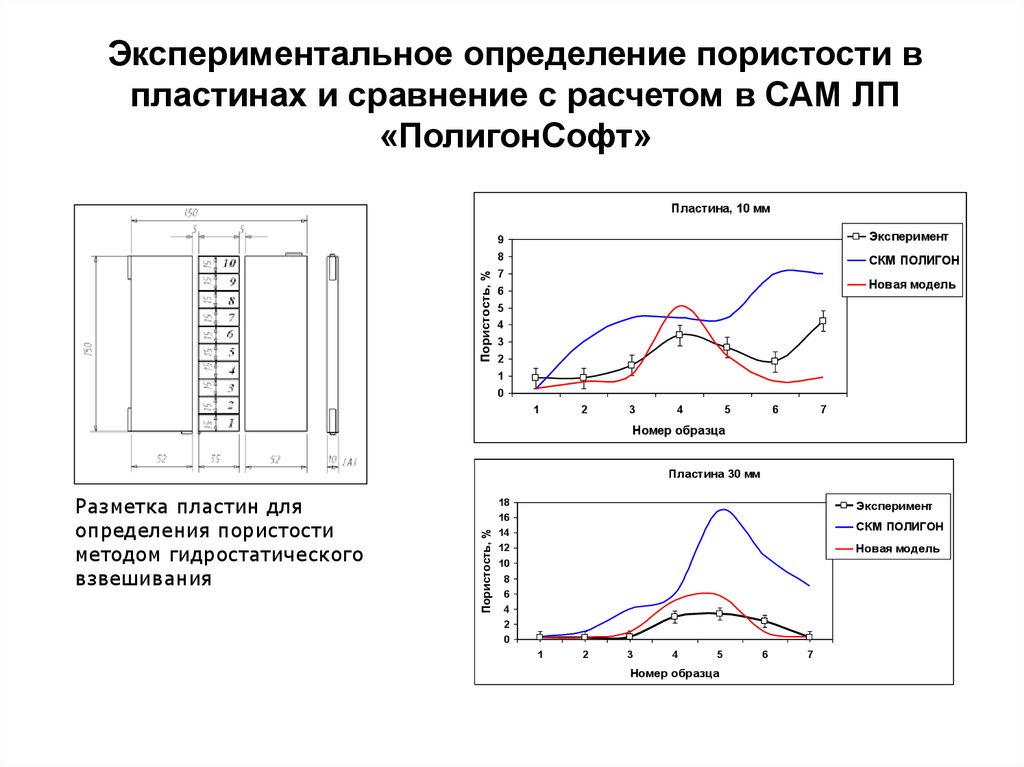
15. Экспериментальное определение пористости в пластинах и сравнение с расчетом в САМ ЛП «ПолигонСофт»

Пористость, %
Пластина, 10 мм
9
Эксперимент
8
СКМ ПОЛИГОН
7
Новая модель
6
5
4
3
2
1
0
1
2
3
4
5
6
7
Номер образца
Разметка пластин для
определения пористости
методом гидростатического
взвешивания
Пористость, %
Пластина 30 мм
18
16
14
12
10
Эксперимент
СКМ ПОЛИГОН
Новая модель
8
6
4
2
0
1
2
3
4
5
Номер образца
6
7