Моделирование процессов термомодифицирования древесины

1. МОДЕЛИРОВАНИЕ ПРОЦЕССОВ ТЕРМОМОДИФИЦИРОВАНИЯ ДРЕВЕСИНЫ

Московский государственный университет леса,
МОДЕЛИРОВАНИЕ ПРОЦЕССОВ
ТЕРМОМОДИФИЦИРОВАНИЯ ДРЕВЕСИНЫ
М.Г.Ермоченков
кафедра теплотехники
2012
1

2. Цель работы

• Разработка математической модели тепло- и массообмена в
древесине при интенсивном тепловом воздействии
• Разработка методов прогнозирования свойств термически
модифицированной древесины
Принятые допущения
- древесина в условиях интенсивного нагрева – многокомпонентная открытая трехфазная
термодинамическая система с физико-химическими превращениями;
- в каждом бесконечно малом объеме материала существует состояние локального
термодинамического равновесия;
- древесина представляет собой капиллярно-пористый композиционный материал, состоящий
из твердых, жидких и газофазных компонентов; рассматривается континуальная модель
материала;
- газовая фаза рассматривается как трех компонентная смесь газов, состоящая из:
а) водяного пара;
б) воздуха;
в) продуктов деструкции древесины;
- конвективный перенос газа внутри древесины описывается уравнением Дарси;
- температуры газовой, жидкой и твердой фаз равны;
- перенос теплоты в древесине осуществляется тепловыми потоками за счет теплопроводности
и конвективного переноса жидкой и газовой фаз;
- масса в жидкой фазе переносится за счет влагопроводности и конвективными потоками;
- масса в газовой фазе переносится конвективными и диффузионными потоками;
- задача решается в одномерной постановке.
2

3. Уравнение переноса массы в твердой фазе:

n1 m1
1
1 , 1
1 1
(1)
Здесь n1 – число твердофазных компонентов,
m1 – число стадий,
γ1 – номер компонента,
Ψ1 – номер стадии.
3

4. Уравнение переноса массы в жидкой фазе:

dW i
W
div j2,v j2,a
d
1
m1
(2)
где j2,а – поток жидкости за счет диффузии,
j2,v – конвективный поток жидкой фазы,
m1 – число стадий,
γ1 – номер компонента.
Уравнение решается с граничными условиями 1-го, 2-го или 3-го
рода на внешних границах материала.
4

5. Уравнения переноса массы в газовой фазе:

n
dW
3,1
div 3,1 v3 3,1 3,1
(3)
d
m
d
3, 2
div 3, 2 v3 3, 2 3, 2
(4)
d
3,3
div 3,3 v3 3,3 3,3
(5)
1
1
1
1
1
1
где ρ – плотность газовой фазы,
i = 1 – водяной пар;
i = 2 –продукты деструкции;
i = 3 –воздух ;
v3– скорость конвективного переноса газовой фазы;
Δ3– скорость диффузионного переноса массы.
Система уравнений решается с граничными условиями 1-го или 2-го
рода на внешних границах материала.
5

6. Уравнение переноса теплоты:

T
в
п
ив
э
c
div q q q U U
(6)
где q - поток теплоты теплопроводностью;
qв – конвективный поток теплоты за счет переноса влаги;
qn – конвективный поток теплоты за счет переноса
паровоздушной смеси;
Uив – источники теплоты за счет физико-химических процессов;
Uэ - источник теплоты за счет внешних воздействий.
Уравнение решается с граничными условиями 1-го, 2-го или
3-го рода на внешних границах материала.
6

7. Скорость протекания многостадийного процесса термической деструкции:

m
Ej
d
nj
j Aj exp
d
j 1
RT
(7)
где j – индекс, соответствующий номеру стадии;
m – число стадий;
Аj – частотный фактор j-й стадии;
Еj – энергия активации j-й стадии;
nj – порядок реакции j-й стадии;
R – газовая постоянная;
Т – температура;
- безразмерная масса стадии.
7

8.

Установка для термогравиметрических исследований в вакууме
6
7
8
9
10
11
12
5
4
3
13
14
2
1
1 – вакуумная камера; 2 – электрическая печь; 3 – Кольцевой тигель; 4 –
весы; 5 – нить; 6 – репер; 7 – плоская спиральная пружина; 8 – крышка
весов; 9 – стекло; 10 – стойка катетометра; 11 – каретка; 12 – окуляр; 13 –
многооборотное сопротивление; 14 – массивное основание
8

9.

Зависимость относительной массы древесины сосны
от времени нагрева (темп нагрева 7 ºС/мин.)
ω, степень разложения
1
0.8
0.6
0.4
0.2
0
0.2
0
10
20
30
40
50
60
70
80
90
100
τ, мин.
9

10. Результаты исследования термической деструкции древесины

Таблица 1
Номер
стадии
Начальная безразмерная
масса стадии
Энергия активации Еj/R
Частотный фактор Аj, с¯¹
Береза
Сосна
Береза
Сосна
Береза
Сосна
1
0,172
0,025
57810
54680
2,377·1051
4,857·1050
2
0,168
0,128
23140
15900
1,362·1018
1,783·1012
3
0,215
0,341
29420
20540
2,784·1021
3,482·1014
4
0,345
0,418
38740
29820
2,623·1026
1,346·1020
5
0,1
0,088
8671
18430
6,517·104
2,338·1010
10

11. Скорость протекания многостадийного процесса парообразования:

E j (φ)
d
nj
j Aj exp
d
j 1
RT
m
(8)
Wi Wк
Wo Wк
(9)
где j – индекс, соответствующий номеру стадии;
m – число стадий;
Аj – частотный фактор j-й стадии;
Еj(φ) – энергия активации j-й стадии;
φ – относительная влажность газовой смеси в порах древесины;
nj – порядок реакции j-й стадии;
R – газовая постоянная;
Т – температура;
- безразмерная масса стадии;
Wi, Wk, W0 – текущее, конечное и начальное влагосодержание в древесине.
11

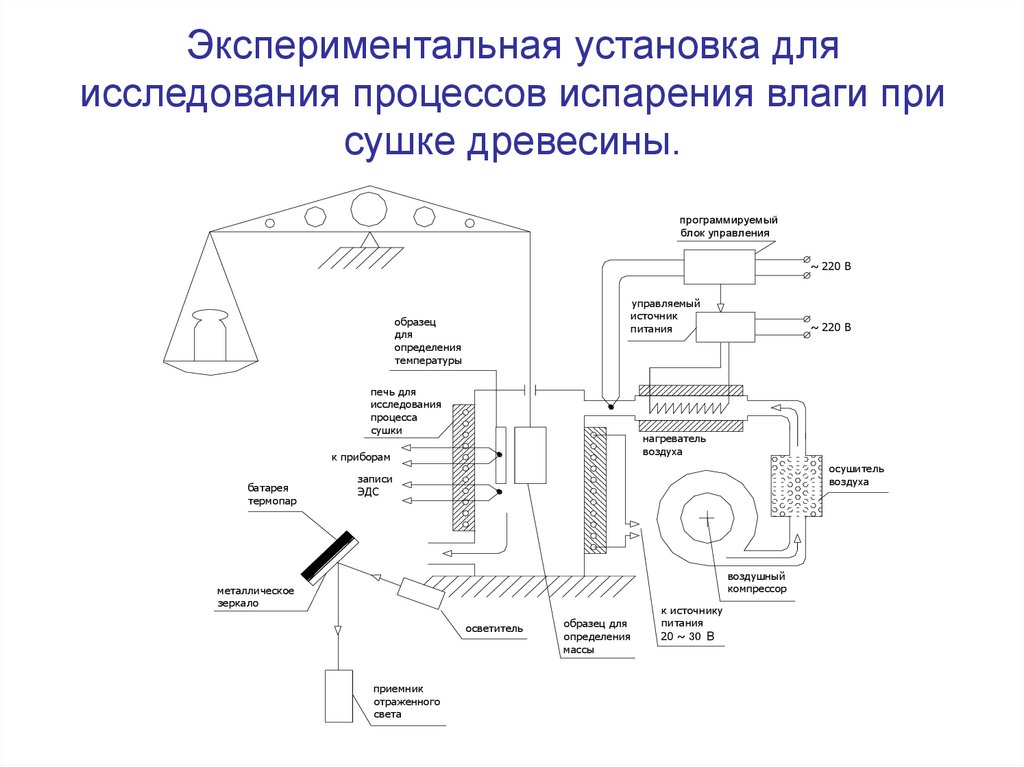
12. Экспериментальная установка для исследования процессов испарения влаги при сушке древесины.

программируемый
блок управления
~ 220 В
управляемый
источник
питания
образец
для
определения
температуры
печь для
исследования
процесса
сушки
нагреватель
воздуха
к приборам
батарея
термопар
~ 220 В
осушитель
воздуха
записи
ЭДС
воздушный
компрессор
металлическое
зеркало
осветитель
приемник
отраженного
света
образец для
определения
массы
к источнику
питания
20 ~ 30 В
12

13. Результаты исследования кинетики сушки древесины березы

Таблица 2
Номер стадии j
Концентрация влаги
j-й стадии j
Энергия активации Еj,
Дж/моль
Частотный фактор Аj, с¯¹
1
0,307 (ω = f(w))
51750
1,64*108
2
0,570 (ω = f(w))
60800
2,80*109
3
0,096 (ω = f(w))
88130
3,70*1013
4
0,027 (ω = f(w))
93700
2,00*1013
E1( ) 0,988 0,162 0,29 2 0,223 3
E 2( ) 0,97 0,953 5,805 2 12,744 3
E 3( ) 0,995 6,196 7,607 3
E 4( ) 0,984 51,667 2 602,564 3
Е1, Е2, Е3, Е4 – значения энергии активации для первой, второй, третьей и четвертой
стадий соответственно;
- относительная влажность воздуха.
13

14. Испарение свободной влаги в порах древесины

Рпара Рнас
Рпара Рнас
Рпара Рнас
Q 1
2 V
r
d 2
0
d
d 2
0
d
d 2
0
d
Q
T
c V
∂Q – количество теплоты, подведенное к объему древесины,
r – скрытая теплота парообразования,
∂Т – изменение температуры,
- плотность материала, с – теплоемкость материала,
x - толщина слоя древесины.
(10)
14

15. Сравнение результатов расчета и эксперимента. Температура поверхности образца.

Т 420
[K]
400
380
360
340
320
300
0
5000
1 10
4
_______ -эксперимент;
1.5 10
4
2 10
4
τ,[с]
- - - - - - - - расчет
15

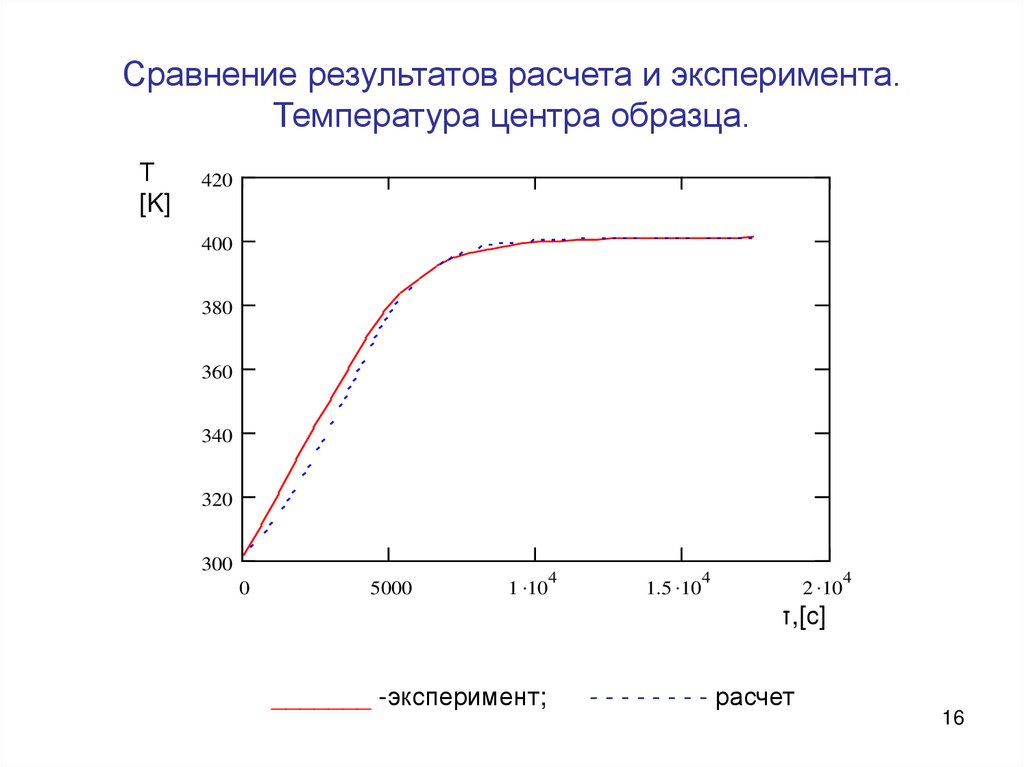
16. Сравнение результатов расчета и эксперимента. Температура центра образца.

Т
[K]
420
400
380
360
340
320
300
0
5000
1 10
4
1.5 10
2 10
4
4
τ,[с]
_______ -эксперимент;
- - - - - - - - расчет
16

17. Сравнение результатов расчета и эксперимента. Масса образца.

0.0175
0.017
0.0165
0.016
0.0155
0.015
0.0145
0
5000
1 10
4
1.5 10
4
2 10
4
τ,[с]
_______ -эксперимент;
- - - - - - - - расчет
17

18. Определение теплофизических свойств термически модифицированной древесины

Плотность древесины рассчитывается из уравнения:
E i
o
d
Аi i exp Ai exp
i 1
R T
0
n
(11)
теплоёмкость древесины
с
1
n
c
i 1
i
i
(12)
18

19. Коэффициент теплопроводности

f j
B 1 B
j B 2 j 1 1 B 2 2 j 1
j
j j 1
B 1 B
j
(13)
B 0,5 A cos
3
при
0 r j 1 0,5
A 1;
2 arccos 1 2 r j 1
при
0,5 rj 1 1
A 1;
2 arccos 2 rj 1 1
19

20. Коэффициент теплопроводности для анизотропной среды

y
η
ξ
φ
x
x cos 2 sin 2 ;
y sin 2 cos 2 ;
(14)
где
и
- коэффициенты теплопроводности древесины
вдоль направлений анизотропии
20

21. Уравнение Дарси

P
w к ,
r
к0
к0 М
к
П
М
n
1
П
n
(15)
(16)
n
,
(17)
Модифицированное уравнение Дарси
dP
1w1 w12 .
dx
(18)
P12 P22
2
G G ,
2 RT
(19)
21

22. Установка для экспериментального исследования проницаемости древесины

22

23. Результаты экспериментального исследования проницаемости поперёк волокон в тангенциальном направлении термомодифицированной

древесины.
Таблица 3
порода
Время
воздействия, [с]
Начальная
масса
образца,
[кг]
Конечная
масса
образца,
[кг]
Перепад
давлений,
[мПа]
Коэффицие
нт
воздухопро
ницаемости
, [с]
–
–
5,97 ·10-3
5,97 ·10-3
0,101
4,48 ·10-12
250
150
6,670 ·10-3
6,145 ·10-3
0,101
4,43 ·10-12
–
–
8,45 ·10-3
8,45 ·10-3
0,101
1,89 ·10-12
250
200
8,3 ·10-3
7,335 ·10-3
0,101
2,14 ·10-12
300
750
7,375 ·10-3
4,845 ·10-3
0,101
3,49 ·10-11
300
750
7,375 ·10-3
4,845 ·10-3
0,051
3,18 ·10-11
–
–
12,580 ·10-3
12,580 ·10-3
0,101
1,16 ·10-11
270
300
12,580 ·10-3
10.055 ·10-3
0,101
1,11 ·10-10
23
Температур
а отжига,
[с]
сосна
берёза

24. График зависимости проницаемости древесины сосны от пористости

6 10
К,[c]
11
5 10
11
4 10
11
3 10
11
2 10
11
1 10
11
0
0.6
0.65
0.7
0.75
0.8
П
0.85
24

25.

9
kf ( 320) 1.227 10
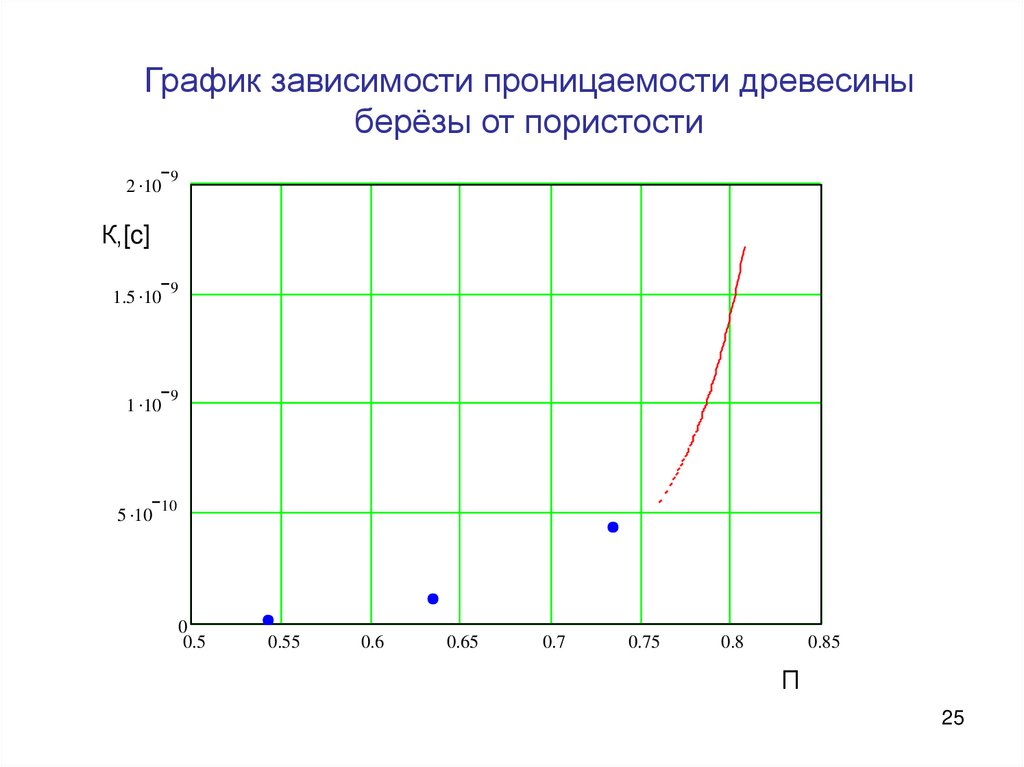
График зависимости проницаемости древесины
берёзы от пористости
2 10
9
К,[c]
1.5 10
9
1 10
9
5 10
10
0
0.5
0.55
0.6
0.65
0.7
0.75
0.8
0.85
П
25

26. Графики изменения массы цилиндрического образца при нагреве в вакууме.

750
М
[мг]
700
650
600
550
500
5
10
15
20
25
30
_________ – расчёт
- - - - - - - - – эксперимент
35
40
τ [мин]
45
26

27. График зависимости коэффициента теплопроводности термически модифицированной древесины сосны от конечной температуры нагрева.

0.13
λ
[Вт/м·К]
0.12
0.11
0.1
0.09
0
50
100
150
200
250
300
350
Т, [С]
27

28.

Зависимость характеристик цвета древесины от
степени термической деструкции в общем виде
n
R( i ) fri ( i )
i 1
n
G ( i ) fgi ( i )
(20)
i 1
n
B( i ) fbi ( i )
i 1
fri ( i ), fg i ( i ), fbi ( i )- функциональные зависимости R, G, B соответственно;
i - номер стадии термической деструкции;
n
- число стадий термической деструкции;
i - степень разложения древесины
28

29.

Функциональные зависимости характеристик
цвета в системе RGB от степени деструкции
древесины
R( 2 , 3 ) 205,74 385,82 2 5883 ( 2 ) 2 84,14 3 570,14 ( 3 ) 2
G( 2 , 3 ) 111,67 114,78 2 4009 ( 2 ) 2 39,13 3 170,04 ( 3 ) 2
(21)
B( 2 , 3 ) 38,14 6,21 2 2495 ( 2 ) 2 99,74 3 180,04 ( 3 ) 2
Где ω2, ω3 – степень завершения второй и третьей стадии термической
деструкции сосны соответственно
29

30. Результаты проверочного эксперимента

R = 113
R = 109
B = 44
B = 49
G = 16
G = 25
Экспериментально
полученный цвет
Расчетный цвет
30

31. Прогнозирование длительной прочности образцов из термически модифицированной древесины

Формула Журкова:
U 0n n
0 exp
R Tn
(22)
Долговечность образцов при термической деструкции:
U
U
U
0 exp 0,0 0 0 exp 0,1 1 f 1 ... 0 exp 0,n n f n
R T
R T
R Tn
(23)
Долговечность образцов из модифицированной древесины сосны:
32800 117,9
27240 58,3
29510 exp
26810
exp
f ( 1 )
R T
R T
Где
f 1 1
(24)
1
0,1
(25)
31