Формула Пика для вычисления площадей многоугольников с дырками

1. Формула Пика для вычисления площадей многоугольников с дырками

2. Формула Пика

Теорема. Пусть A – число целочисленных
точек
внутри
многоугольника,
B
–
количество целочисленных точек на его
границе, S – его площадь. Тогда
B
S A 1.
2
Пример.
А 7, B 8
8
S 7 1 10
2

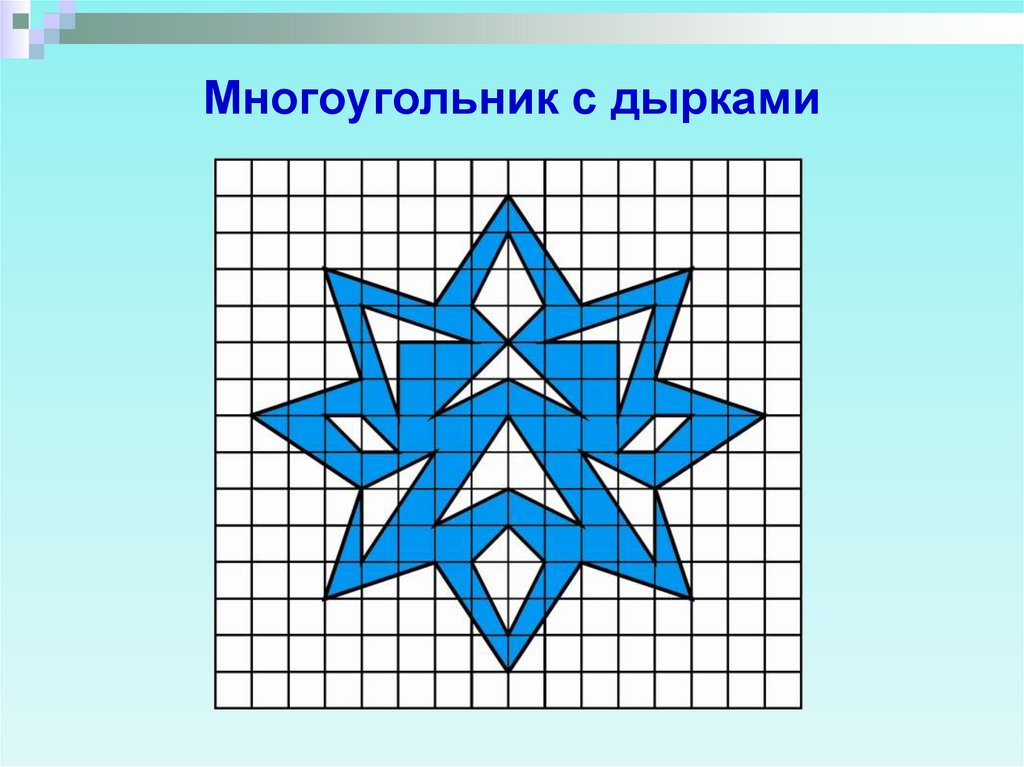
3. Многоугольник с дырками

4. Цели работы

1) выявить зависимость между расположением
дырок внутри многоугольника и изменением
формулы Пика для вычисления площади
такого многоугольника;
2) получить изменённую формулу Пика для
вычисления
площади
многоугольника
с
некоторыми видами дырок.

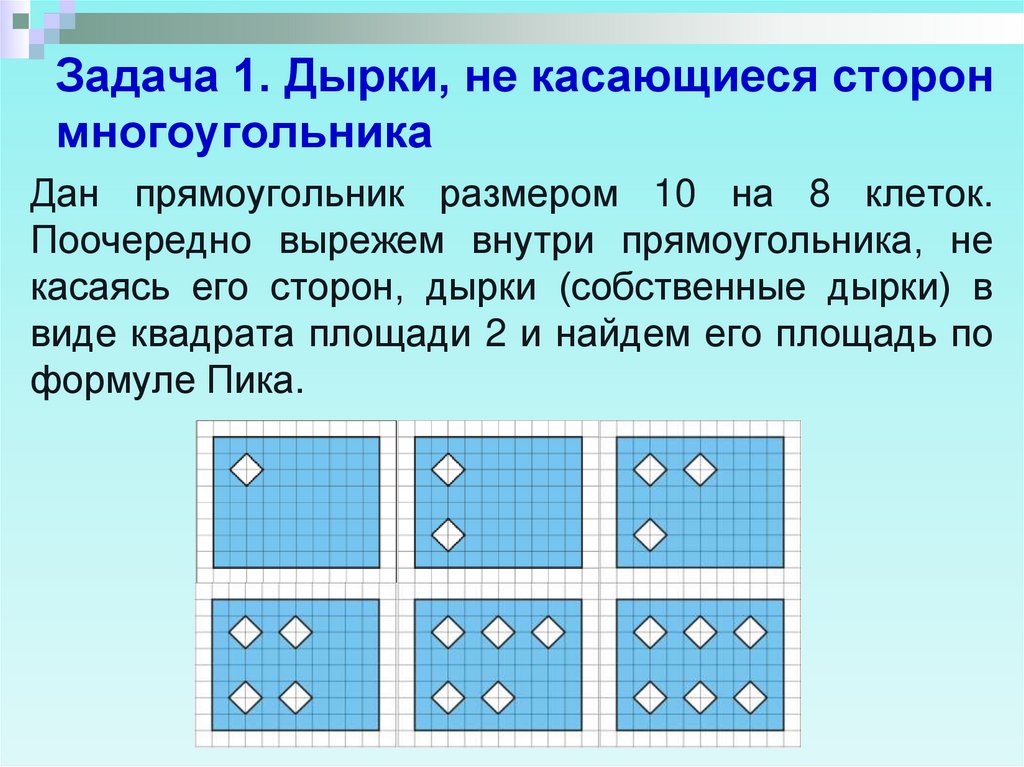
5. Задача 1. Дырки, не касающиеся сторон многоугольника

Дан прямоугольник размером 10 на 8 клеток.
Поочередно вырежем внутри прямоугольника, не
касаясь его сторон, дырки (собственные дырки) в
виде квадрата площади 2 и найдем его площадь по
формуле Пика.

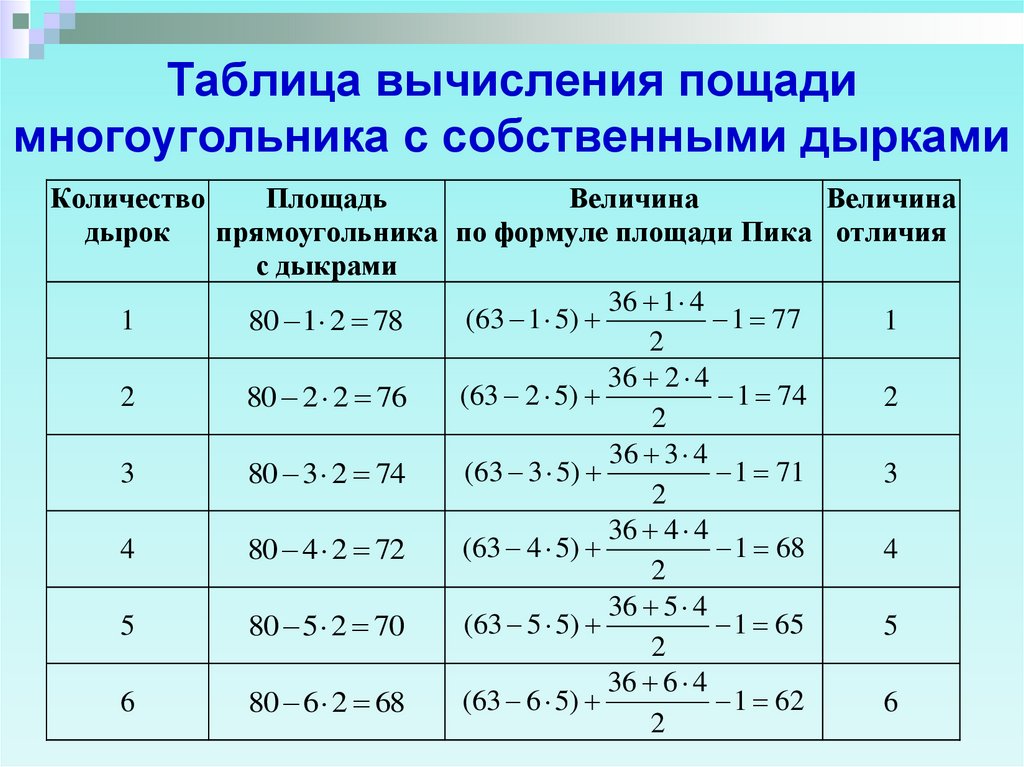
6. Таблица вычисления пощади многоугольника с собственными дырками

Количество
Площадь
Величина
Величина
дырок
прямоугольника по формуле площади Пика отличия
с дыкрами
36 1 4
(
63
1
5
)
1 77
1
1
80 1 2 78
2
36 2 4
(63 2 5)
1 74
2
2
80 2 2 76
2
36 3 4
(63 3 5)
1 71
3
3
80 3 2 74
2
36 4 4
(
63
4
5
)
1 68
4
4
80 4 2 72
2
36 5 4
(
63
5
5
)
1 65
5
5
80 5 2 70
2
36 6 4
(63 6 5)
1 62
6
6
80 6 2 68
2

7. Формула вычисления пощади многоугольника с собственными дырками

Теорема 1. Площадь произвольного
многоугольника с собственными дырками равна
B
S A 1 k ,
2
где A – количество собственных внутренних
точек многоугольника с дырками,
B – количество граничных точек
многоугольника (включая точки на границе
дырок),
k – количество собственных дырок внутри
многоугольника.

8. Доказательство теоремы 1

BM
S S M S D AM
1
2
B1
B2
Bk
A1 1 A2
1 Ak
1
2
2
2
Количество собственных внутренних точек многоугольника с дырками
A AM A1 A2 Ak B1 B2 Bk
Количество граничных точек многоугольника (включая границы дырок)
B BM B1 B2 Bk
Подставляя выражения для AM и BM в формулу, получим
B B1 Bk
S A A1 Ak B1 Bk
2
B1 Bk
1 A1 Ak
k
2

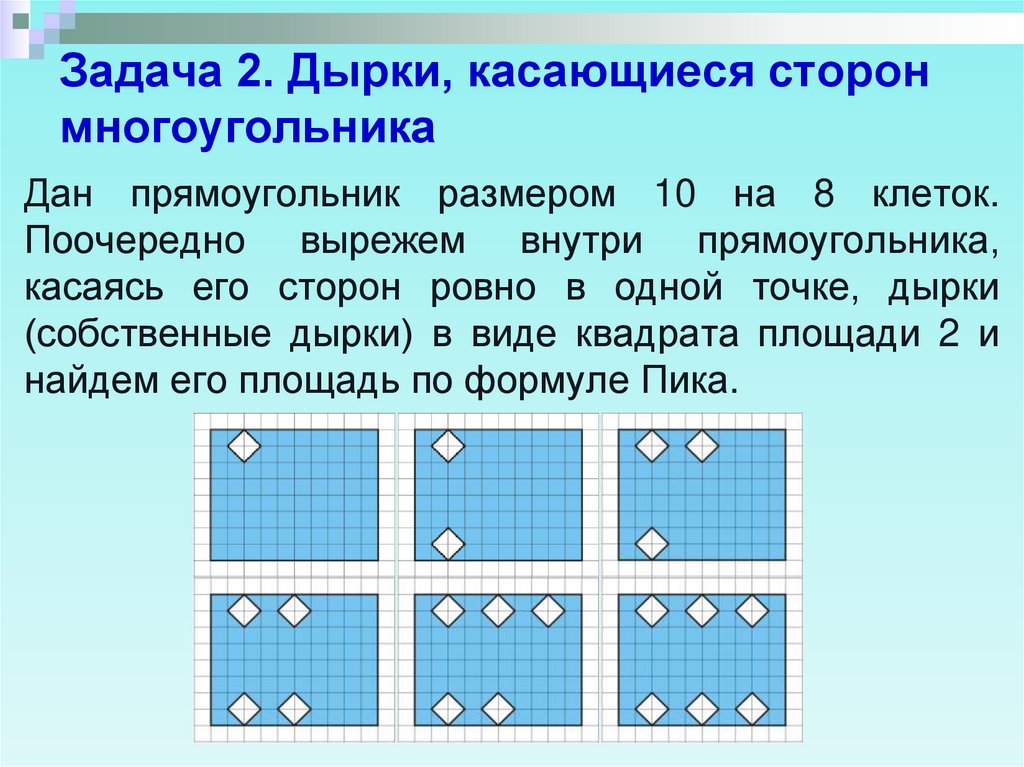
9. Задача 2. Дырки, касающиеся сторон многоугольника

Дан прямоугольник размером 10 на 8 клеток.
Поочередно вырежем внутри прямоугольника,
касаясь его сторон ровно в одной точке, дырки
(собственные дырки) в виде квадрата площади 2 и
найдем его площадь по формуле Пика.

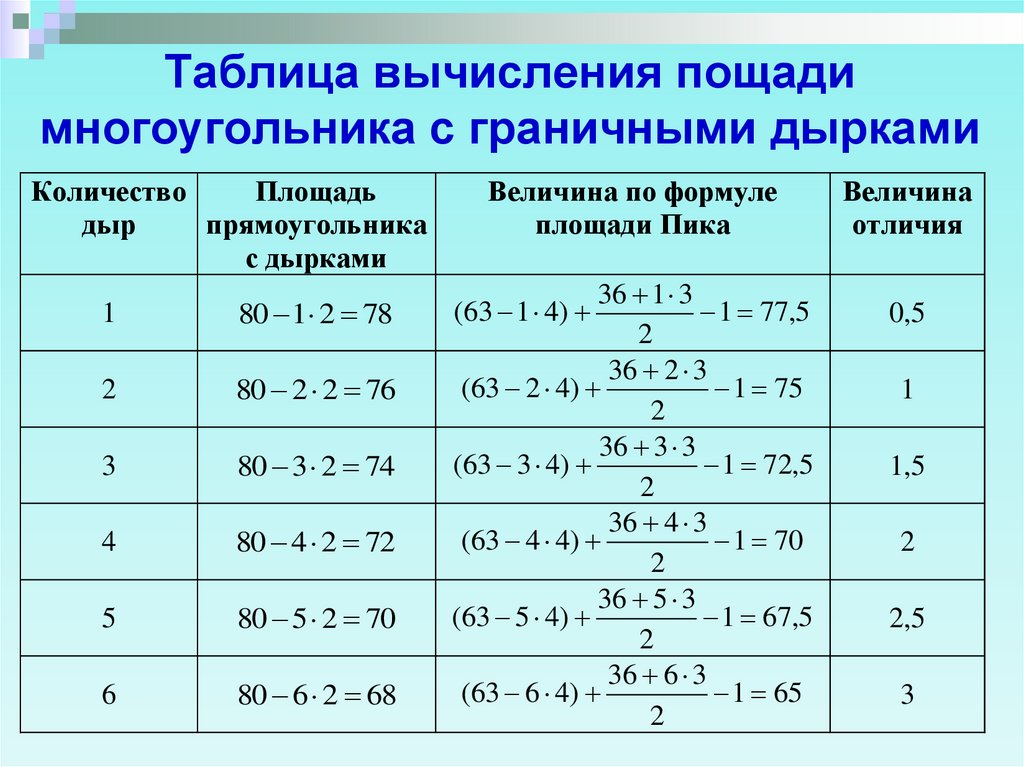
10. Таблица вычисления пощади многоугольника с граничными дырками

Количество
Площадь
дыр
прямоугольника
с дырками
1
80 1 2 78
2
80 2 2 76
3
80 3 2 74
4
80 4 2 72
5
80 5 2 70
6
80 6 2 68
Величина по формуле
площади Пика
36 1 3
(63 1 4)
1 77,5
2
36 2 3
(63 2 4)
1 75
2
36 3 3
(63 3 4)
1 72,5
2
36 4 3
(63 4 4)
1 70
2
36 5 3
(63 5 4)
1 67,5
2
36 6 3
(63 6 4)
1 65
2
Величина
отличия
0,5
1
1,5
2
2,5
3

11. Формула вычисления пощади многоугольника с граничными дырками

Теорема
2.
Площадь
произвольного
многоугольника с граничными дырками равна
B
k
S A 1 ,
2
2
где A – количество собственных внутренних
точек многоугольника с дырками,
B
–
количество
граничных
точек
многоугольника (включая границы дырок),
k – количество граничных дырок внутри
многоугольника.

12. Доказательство теоремы 2

BM
S S M S D AM
1
2
B1
B2
Bk
A1 1 A2
1 Ak
1
2
2
2
Количество собственных внутренних точек многоугольника с дырками
A AM A1 A2 Ak B1 1 B2 1 Bk 1 ,
Количество граничных точек многоугольника (включая границы дырок)
B BM B1 1 B2 1 Bk 1 .
Подставляя выражения для AM и BM в формулу, получим
S S M S D A A1 Ak B1 Bk k
B B1 Bk k
B1 Bk
1 A1 Ak
k
2
2

13. Формула вычисления пощади многоугольника с дырками двух видов

Теорема 3. Площадь произвольного многоугольника
с собственными и граничными дырками равна
B
m
S A 1 k ,
2
2
A – количество собственных внутренних точек
многоугольника с дырками,
B – количество граничных точек многоугольника
(включая точки на границе дырок),
k – количество собственных дырок многоугольника,
m – количество граничных дырок многоугольника.

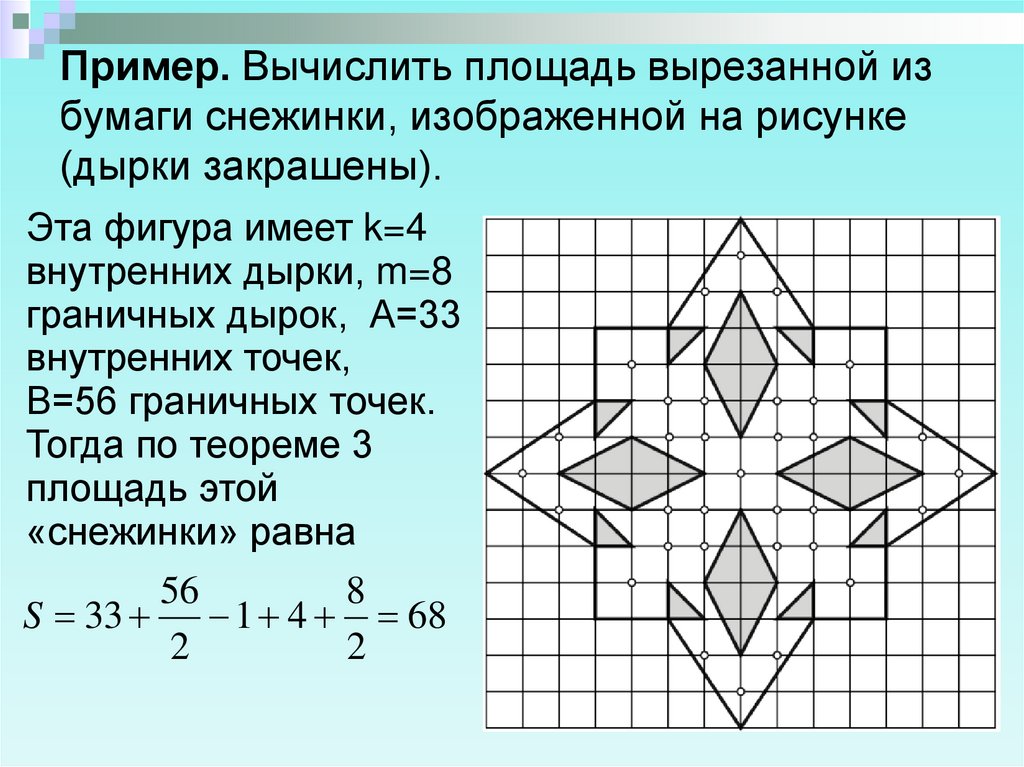
14. Пример. Вычислить площадь вырезанной из бумаги снежинки, изображенной на рисунке (дырки закрашены).

Эта фигура имеет k=4
внутренних дырки, m=8
граничных дырок, А=33
внутренних точек,
В=56 граничных точек.
Тогда по теореме 3
площадь этой
«снежинки» равна
56
8
S 33
1 4 68
2
2

15. Заключение

В работе рассмотрены два различных случая
расположения дырок внутри многоугольника: без
касания сторон многоугольника и с касанием сторон
многоугольника в одной точке.
Основные результаты работы :
1) мы установили, что существует зависимость
между расположением дырок внутри многоугольника
и изменением формулы Пика для вычисления
площади такого многоугольника;
2) получили изменённые формулы Пика для
вычисления площади многоугольника с тремя видами
дырок.

16. Спасибо за внимание!