Похожие презентации:
Показательная и логарифмическая функции
1. Решение типовых задач из сборника ЕНТ по разделу: «Показательная и логарифмическая функции»
2. Основные понятия и формулы
ху
а
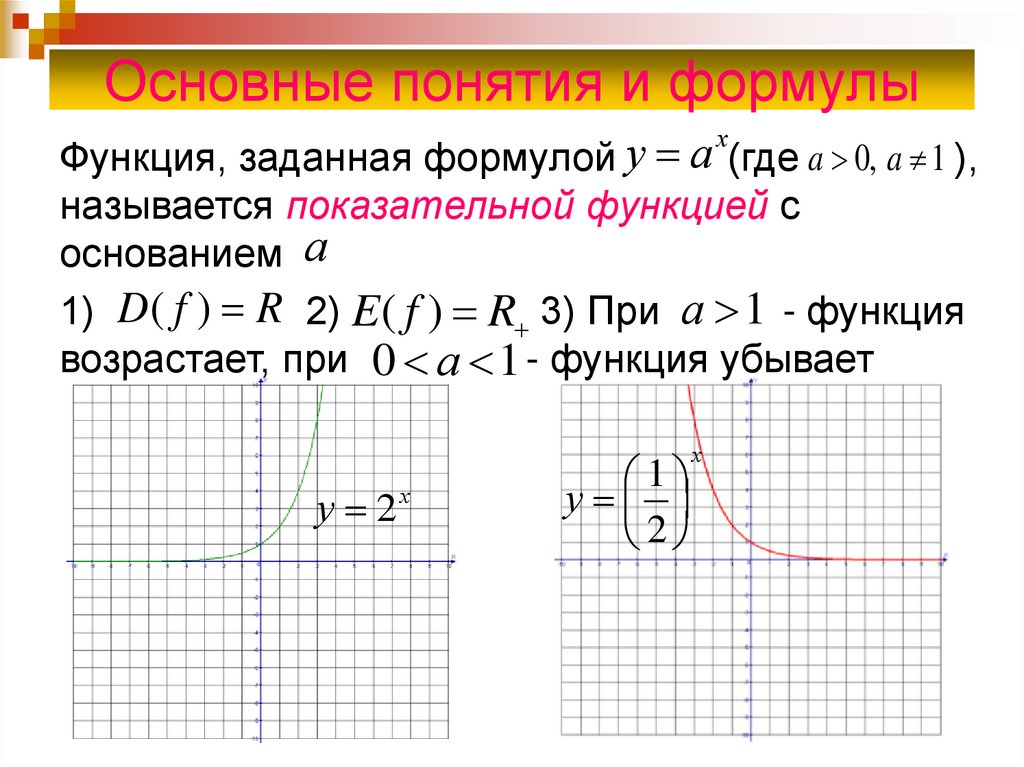
Функция, заданная формулой
(где a 0, a 1 ),
называется показательной функцией с
основанием а
1) D ( f ) R 2) E ( f ) R 3) При а 1 - функция
возрастает, при 0 а 1 - функция убывает
у 2
х
1
у
2
х
3. Основные понятия и формулы
Функция, заданная формулой у log a xназывается логарифмической функцией с
основанием а (где a 0, a 1 )
1) D( f ) R 2) Е ( f ) R 3) При а 1 - функция
возрастает, при 0 а 1 - функция убывает
у 2
1
у
2
х
у log 2 x
х
у log 1 x
2
4. Основные понятия и формулы
Логарифмом числа b по основанию а называютпоказатель степени N , в которую нужно возвести
число а , чтобы получить число b , т.е. log a b N
loga b
a
b - основное логарифмическое тождество
Основные свойства логарифмов:
1) log a 1 0
5) log a x p p log a x
1
2) log a a 1
6) log a n x log a x
n
log b x
3) log a xy log a x log a y 7) log a x
log b a
x
4) log a log a x log a y
y
5. Основные понятия и формулы
Натуральный логарифм: log е х ln xДесятичный логарифм: log 10 х lg x
Производная и первообразная
1) (e ) e
x
x
a
5) a dx
C
ln a
x
x
x
2) (a ) a ln a
x
1
3) (ln x)
x
4) e dx e C
x
x
6) ln x dx x ln x x C
6. ПРИМЕР 1
Решите неравенство:log 2 ( х 20) 3
Решение:
log 2 ( х 20) 3
x 20 0
x 20
;
x ( 20; 12)
3
x 20 2 , т.к. 2 1 x 12
Ответ: (-20; -12)
7. ПРИМЕР 2
Решите неравенство:Варианты ответа:
2 log 2 х 3
A)( 3;0) B )( 2 2 ;2 2 C )( 0;2 2 ) D )( ;2 2 ) E )( 3;3)
Решение:
3
2 log 2 х 3; log 2 х
2
x 0
x 0
x 0
;
;
x (0;2 2 )
3
2
x 8 x 2 2
x 2 , т.к. 2 1
х (0;2 2 )
8. ПРИМЕР 3
Решить неравенство:log 1 ( x 2 2 x) 1
3
Решение:
log 1 ( x 2 2 x) 1;
3
+
+
0
2
_
x2 2x 0
-1
3
1
2
1
1
x 2 x , т.к. <1
3
3
x( x 2) 0
2 4
D 16, x1, 2
, х1 1, х2 3
2
2
x 2x 3 0
Ответ: х ( 1;0) ( 2;3)
9. ПРИМЕР 4
Решите систему неравенств:Решение:
x 1 0
x 1 4, т.к. 2 1;
( x 7)( x 5) 0
x 1
;
x 3
( x 7)( x 5) 0
log 2 ( x 1) 2
x 7
0
x 5
_
-5
7
3
x 3;7
Ответ:
x 3;7
10. ПРИМЕР 5
Решите неравенство:log 3 0,2
0
x 3
Решение:
ОДЗ : х 3
т.к. log 3 0,2 0 x 3 0
x 3
x ( 3; )
Ответ:
x ( 3; )
11. ПРИМЕР 6
Сколько целых решений имеет неравенство:Решение: ОДЗ : x 0, x 1
log x 3 y;
1 5 log x 3 6 log 2x 3 0
6 y2 5y 1 0
6 y2 5y 1 0
D 1;
y1, 2
1) log x 3
1
3
1
3
5 1
;
12
1
;
3
1
2) log x 3
2
у1
1
2
x 3
x 3
x1 27
x2 9
у2
1
2
+
_
9
+
27
x (9;27)
Подсчетом определяем, что количество целых решений: 10; 11;
12;…25; 26 равно 17
Ответ: 17
12. Уровень В Решите неравенство:
lg x 4 lg 2x 3 lg 1 2xОтвет : х 1,5; 1
13. Уровень В Решите неравенство: Ответ:
14. Уровень С Решите неравенство: Ответ:
Ответ:15. Front Work
26
log
(
5
x
)
log
(
5
x
)
9
1. Найдите наибольшее целое решение неравенства:
2
2
2. Решите неравенство:
log 2 log х 1 (3х 2) 0
log3 x
log3 2
2
56
6
х
3. Решите неравенство:
Ответы:
1) 3
1 1
2) ;
2 3
3) 0; 27











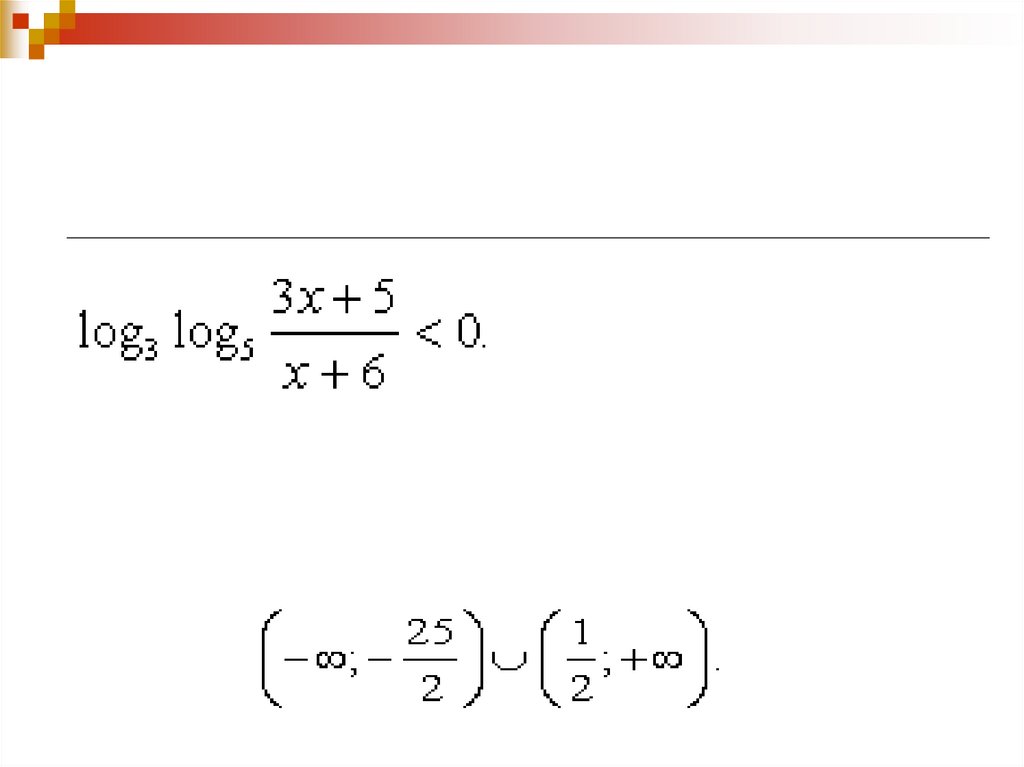




 Математика
Математика








