Равносильность неравенств

1. Равносильность неравенств

25.02

2.

• Решением
неравенстваf(x)>g(x) называют
всякое значение переменной x,
которое обращает заданное
неравенство с переменной в верное
числовое неравенство.
• Термин решение используют в трёх
смыслах: как общее решение, как
частное решение и как процесс.

3.

4.

• Определение 1.
• Два неравенства с одной
переменной f(x)>g(x) и p(x)>h(x) называют равносильными,
если их решения (т.е. множества частных решений)
совпадают.
• Использование знака > непринципиально, может быть любой
другой знак неравенства как строгого, так и нестрогого.
• Определение 2.
• Если решение неравенства f(x)>g(x)
(1)
• содержится в решении неравенства p(x)>h(x), (2)
• то неравенство (2) называют следствием неравенства (1).

5.

• Неравенство x2>9 является следствием
неравенства 2x>6.В самом деле,
решив каждое неравенство, получим:
• x2−9>0(x−3)⋅(x+3)>0x∈(−∞;−3)∪(3;+∞)
и
2x>6x>3x∈(3;+∞)
• Решение второго неравенства
является частью решения первого,
поэтому первое неравенство —
следствие второго неравенства.

6.

• Решение неравенств, встречающихся в
школьном курсе, основано на шести
теоремах о равносильности:
• Теорема 1.
• Если какой-либо член неравенства
перенести из одной части неравенства
в другую с противоположным знаком,
оставив знак неравенства без
изменения, то получится неравенство,
равносильное данному.

7.

• Теорема 2.
• Если обе части неравенства возвести в
одну и ту же нечётную степень, оставив
знак неравенства без изменения, то
получится неравенство, равносильное
данному.

8.

Теорема 3.
Показательное неравенство
f(x)
g(x) равносильно:
а
> а
а) неравенству того же
смысла f(x)>g(x), если a>1;
• б) неравенству противоположного
смысла f(x)<g(x), если 0<a<1

9.

• Теорема 4.
• a) Если обе части неравенства f(x)>g(x) умножить на одно и то
же выражение h(x), положительное при всех x из области
определения (области допустимых значений переменной)
неравенства f(x)>g(x), оставив при этом знак неравенства без
изменения, то получится неравенствоf(x)⋅h(x)>g(x)⋅h(x),
равносильное данному.
• б) Если обе части неравенства f(x)>g(x) умножить на одно и то
же выражение h(x), отрицательное при всех x из области
определения неравенства f(x)>g(x), изменив при этом знак
неравенства на противоположный, то получится
неравенство f(x)⋅h(x)<g(x)⋅h(x), равносильное данному.

10.

• Теорема 5.
• Если обе части неравенства f(x)>g(x) неотрицательны в области
его определения (в ОДЗ), то после возведения обеих частей
неравенства в одну и ту же чётную степень n получится
неравенство того же смысла f(x)n>g(x)n, равносильное данному.
• Теорема 6.
• Если f(x)>0 и g(x)>0, то логарифмическое
неравенство logaf(x)>logag(x) равносильно:
• а) неравенству того же смысла f(x)>g(x), если a>1;
• б) неравенству противоположного смысла f(x)<g(x),
если 0<a<1.

11.

Метод решения хорош, если с самого
начала мы можем предвидеть – и в
последствии подтвердить это, - что,
следуя этому методу, мы достигнем
цели.
Г. Лейбниц

12.

Схема выполнения равносильных преобразований некоторых
иррациональных неравенств
2 k 1
f ( x) g ( x)
f ( x) g ( x)
2 k 1
2 k 1
f ( x) g ( x)
f ( x) g ( x)
Знак неравенства сохраняется
2 k 1

13.

f ( x) g ( x)
2k
g ( x) 0,
f ( x) g ( x)
f ( x) 0,
g ( x) 0
или
2k
2k
f ( x) g ( x)
f ( x) 0,
g ( x) 0,
f ( x) g ( x)
2k

14.

2k
f ( x ) 2 k g ( x)
f ( x) g ( x),
g ( x) 0

15.

Схема выполнения равносильных преобразований неравенств,
содержащих знак модуля
f ( x) g ( x)
f ( x) g ( x)
или
f ( x) g ( x)
f ( x) g ( x)
f ( x) g ( x),
f ( x) g ( x)

16.

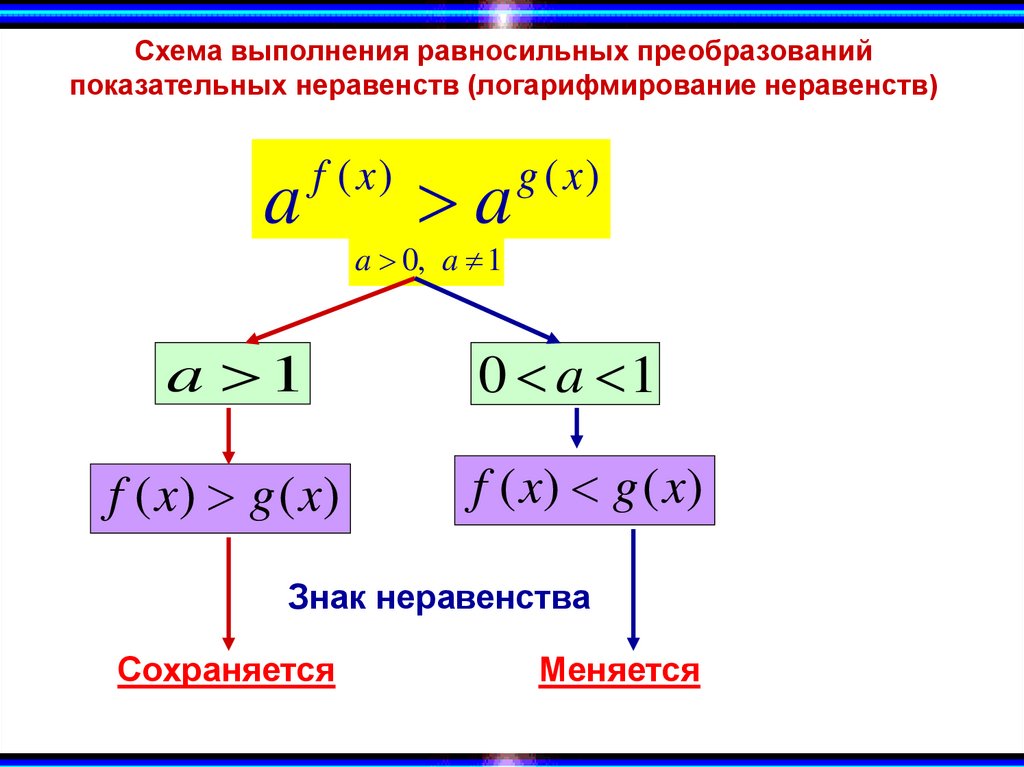
Схема выполнения равносильных преобразований
показательных неравенств (логарифмирование неравенств)
a
f ( x)
a 1
f ( x) g ( x)
a
g ( x)
a 0, a 1
0 a 1
f ( x) g ( x)
Знак неравенства
Сохраняется
Меняется

17.

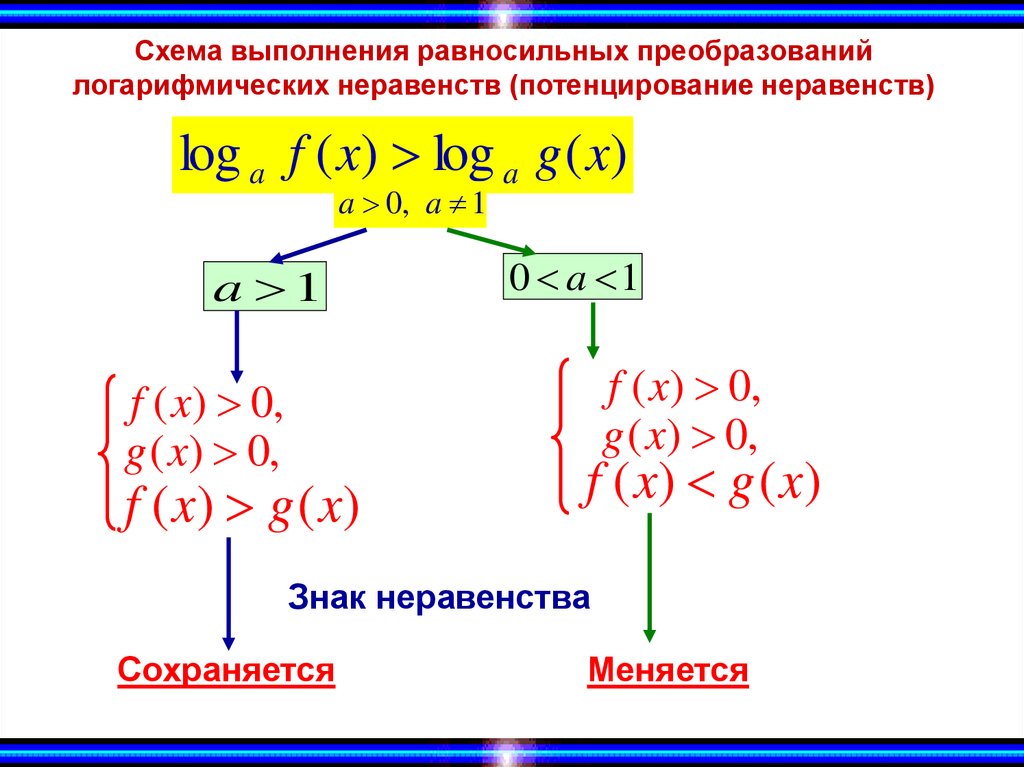
Схема выполнения равносильных преобразований
логарифмических неравенств (потенцирование неравенств)
log a f ( x) log a g ( x)
a 0, a 1
a 1
0 a 1
f ( x) 0,
g ( x) 0,
f ( x) 0,
g ( x) 0,
f ( x) g ( x)
f ( x) g ( x)
Знак неравенства
Сохраняется
Меняется

18.

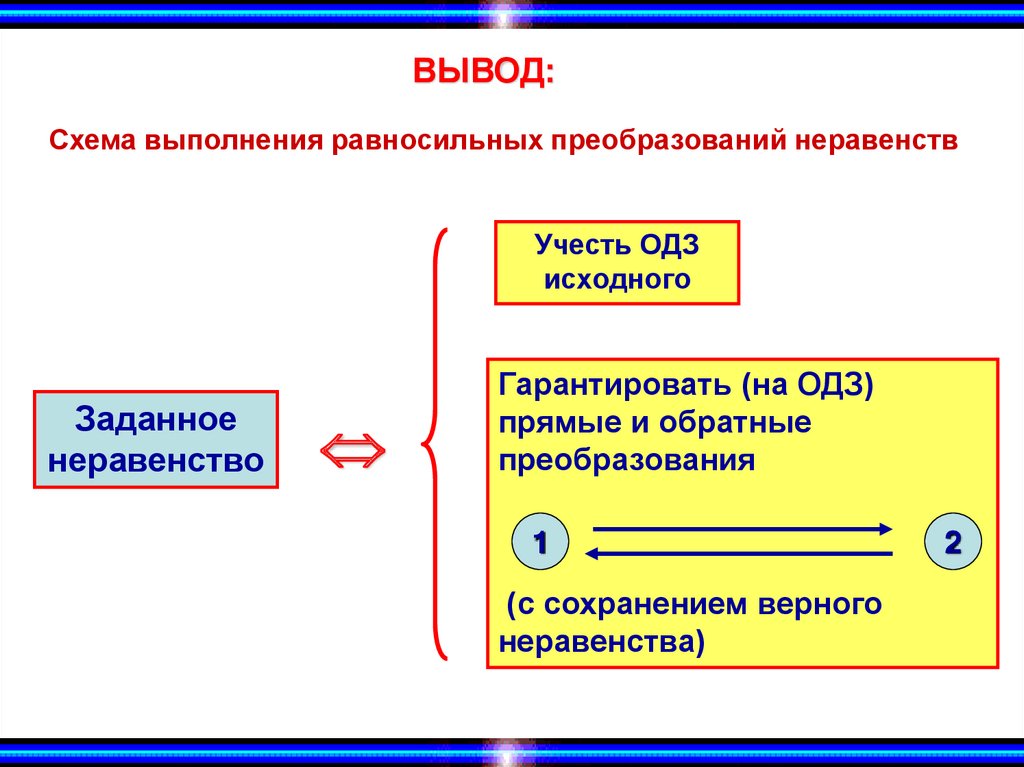
ВЫВОД:
Схема выполнения равносильных преобразований неравенств
Учесть ОДЗ
исходного
Заданное
неравенство
Гарантировать (на ОДЗ)
прямые и обратные
преобразования
1
(с сохранением верного
неравенства)
2

19.

1.
Решите неравенство:
log 7 ( x 3) 1
(- 3 ; 4)
2 х 1
3
1
9
[- 0,5; + )
2. Найдите область определения функции
y log 9 x 2
12
[ 81; + )
y
1
2
5 10 x
[ 0,1; + )
1
16

20.

РАНОСИЛЬНОСТЬ
НЕРАВЕНСТВ НА
МНОЖЕСТВАХ.
ДРУГИЕ
ПРЕОБРАЗОВАНИЯ
НЕРАВЕНСТВ

21.

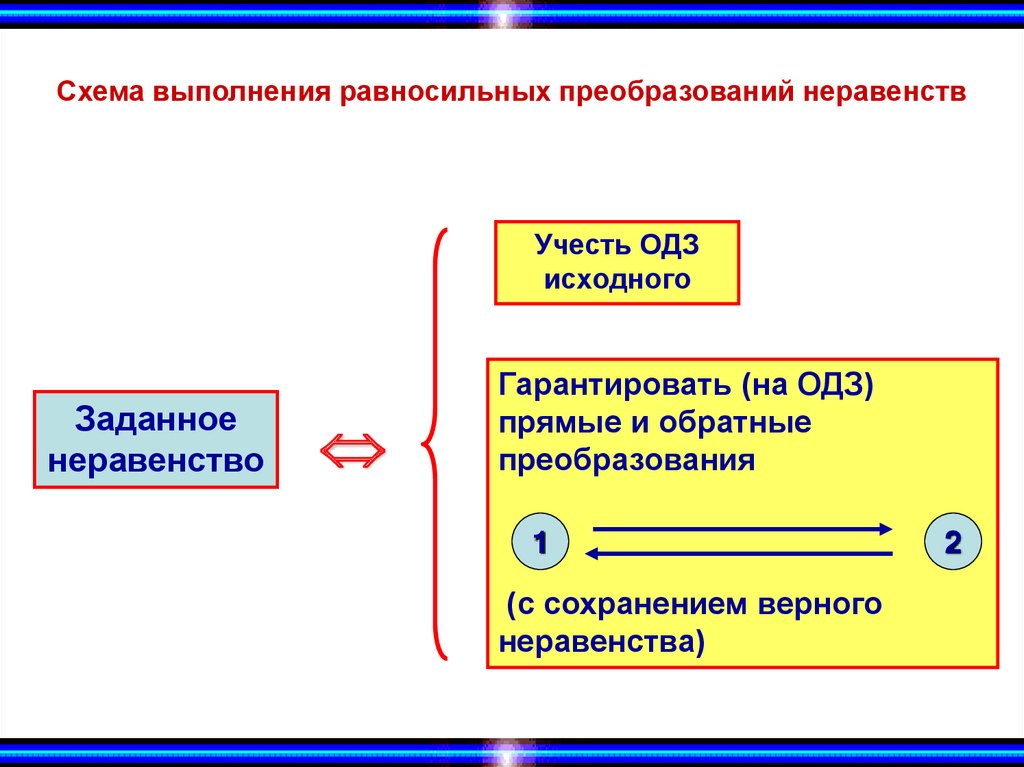
Схема выполнения равносильных преобразований неравенств
Учесть ОДЗ
исходного
Заданное
неравенство
Гарантировать (на ОДЗ)
прямые и обратные
преобразования
1
(с сохранением верного
неравенства)
2

22.

1. Приведение подобных членов неравенства
( x 1) 2 5 x 2 3x 2 x
Решение:
x 0,
( x 1) 2 5 x 2 3x 2 x
1).
x 0,
x 2 x 1 5 x 2 3x 2 x
( x 0,2)( x 1) 0
5 x 2 3x 2 x x 2 x 1 0
5x 2 4 x 1 0
+
5x 4 x 1 5( x 0,2)( x 1)
2
-0,2
0
[ 0 ; 1)
Ответ: [ 0 ; 1)
+
1
х

23.

2. Применение некоторых формул
log 2 x log 2 ( x 4) 2
Решение:
x 0,
x 4,
1).
x( x 4) 4
x2 4x 4
x2 4x 4 0
log 2 x( x 4) log 2 4
x 2 4 x 4 ( x ( 2 8 ))( x ( 2 8 ))
x 0,
x 4,
( x ( 2 8 ))( x ( 2 8 )) 0
+
2 8
-4
Ответ:
+
0
2 8
(0; 2 8 )
х

24.

Применение знаний и способов действий
№ 9.37 (а), № 9.39 (а)
САМОСТОЯТЕЛЬНАЯ РАБОТА
Задание №1
Задание № 2
Задание № 3
№ 9.37 (г),
№ 9.38 (а),
№ 9.40* (г),
№ 9.39 (г)
№ 9.40* (а)
№ 9.41* (а)

25.

ДОМАШНЕЕ ЗАДАНИЕ
1. п. 9.5, № 9.38 (б), № 9.39 (б), № 9.40 (б)
2. Дополнительно:
1. На «4»: C1 Найдите наибольшее значение
функции f ( x) 3(2 x 6) 4 (2 x 6) 5 при x 3 1 .
2. На «5»: C3 Найдите все значения a, при
каждом из которых неравенство
a (3 cos x 1 1)
3
x
3 10 3 x 4 a
0 не имеет решений.