Логарифмические неравенства

1.

Лекция по алгебре.
Тема: логарифмические
неравенства.
Преподаватель математики Хохлова С.Н., Мещенко Н.В.

2.

Определение:
Неравенства, содержащие переменную
под знаком логарифма, называются
логарифмическими.
Например:
1) log5 x 2;
2) lg( x 5) 5;
3) ln( x 1) ;
4) log
3
2
( x 2 x 6)
25 2

3.

I. Типы простейших
логарифмических неравенств
Неравенства вида
1) loga x b или
loga x b
называются простейшими
логарифмическими неравенствами
Неравенства можно переписать
loga x loga
b или
a
loga x loga a
b

4.

Решение логарифмических неравенств
основано на свойстве монотонности
функции y = logat : при a > 1
логарифмическая функция возрастает и
при
0 < a < 1 убывает.
y
y
y = logat, a > 1
0
1
t
0
y = logat, 0 < a < 1
1
t

5.

Методы решения
логарифмических неравенств.
І) Неравенство вида logaf(x) > c (или < c ).
Если a > 1,то
logaf(x) > c,
logaf(x) > c logaa , функция y = logat
возрастает на R+ и
c
logaf(x ) > logaa .
неравенствоlogaf(x)> c
равносильно системе
a>1
f(x) > 0 – это ОДЗ
или
c
f(x) > a – это монотонность
f(x) > ac

6.

Пример. Решить неравенство
log7(4x + 1) 2
Решение.
log7(4x + 1) log749
Так как (a = 7 > 1)
4x + 1 > 0 – это ОДЗ
4x + 1 49
4x + 1 49,
x 12
Ответ: x 12 .

7.

2) Если 0 < a < 1, то функция y = logat
убывает на R+ и неравенство
logaf(x) > c равносильно системе
f(x) > 0 – это ОДЗ
f(x) < ac – это монотонность
Систему в этом случае упростить
нельзя.

8.

Пример. Решить неравенство
log1/2(1 – x) > 2
Решение.
log1/2(1 – x) > log1/2(1/4)
1 – x > 0 – это ОДЗ
1 – x < 1/4 (a = 1/2 < 1)
3/4 < x < 1
x<1
x > 3/4
Ответ: ( 0,75; 1) .

9.

І І. Неравенство вида logaf(x) > logaφ(x)
или logaf (x) < logaφ(x).
1) Если a > 1, то функция y = logat
возрастает на R+ и неравенство
log a f (x) > log aφ(x) равносильно системе
f(x) > 0
– это ОДЗ
φ(x) > 0
f(x) > φ(x) – это монотонность
f(x) > φ(x)
φ(x) > 0

10.

Пример. Решить неравенство
lgx2 > lg(5x – 4)
Решение.
x2 > 5x – 4
5x – 4 > 0
x2
>0
– это ОДЗ
5x – 4 > 0
x2 > 5x – 4 (a = 10 > 1)
(x – 1)(x – 4) > 0
x > 4/5
1
4
x
4/5
Ответ: (0,8;1) (4;∞).

11.

І І. Неравенство вида
logaf(x) > logaφ(x) или logaf (x) < logaφ(x).
2) Если 0 < a < 1, то функция y = logat
убывает на R+ и неравенство
logaf(x) > logaφ(x) равносильно системе
f(x) > 0
– это ОДЗ
φ(x) > 0
f(x) < φ(x) – это монотонность
φ(x) > f(x)
f(x) > 0

12.

Пример. Решить неравенство
log1/3(3x – 4) ≥ log1/3(x2 – 2)
Решение.
3x – 4 > 0
– это ОДЗ
x2 – 2 > 0
3x – 4 ≤ x2 – 2 (a = 1/3 < 1)
(x – 1)(x – 2) ≥ 0
x > 4/3
x2 – 2 ≥ 3x – 4
3x – 4 > 0
1
4/3
2
Ответ: [ 2; ∞).
x

13.

Простейшие логарифмические
неравенства.
f x 1,
logа f x 0, logа f x loga 1,
a 1
0 f x 1,
logа f x loga 1,
0 a 1
0 a 1
1)
a 1
logа f x 0,
2)
0 a 1
a 1
logа f x 0,
3)
a 1
logа f x loga 1,
0 f x 1,
a 1
a 1
logа f x 0,
4)
0 a 1
logа f x loga 1,
f x 1,
0 a 1
0 a 1

14.

І І І) Неравенства, требующие предварительных
преобразований.
1) Находят ОДЗ неравенства.
2) Преобразуют неравенство к виду І
или І І и решают полученное
неравенство, используя свойство
монотонности.
3) Находят пересечение множества
решений с ОДЗ неравенства и
записывают ответ.

15.

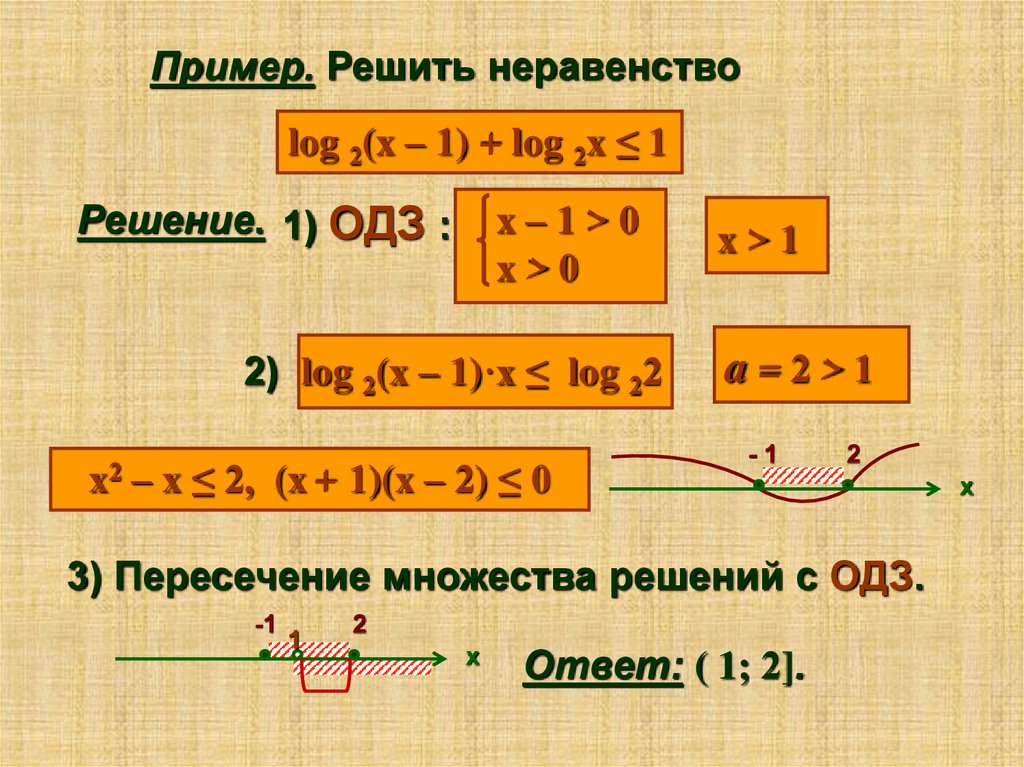
Пример. Решить неравенство
log 2(x – 1) + log 2x ≤ 1
Решение. 1) ОДЗ :
x–1>0
x>0
2) log 2(x – 1)·x ≤ log 22
x2
– x ≤ 2, (x + 1)(x – 2) ≤ 0
x>1
a=2>1
-1
2
3) Пересечение множества решений с ОДЗ.
-1
1
2
x
Ответ: ( 1; 2].
x

16.

III.Метод замены переменной в
логарифмическом неравенстве.
Пример. Решить неравенство
Решение.
lg x 3 lg x 3
1
lg x 1
2
Пусть lgx = t, t – любое число, тогда
2
t
3
t
3
неравенство примет вид
1 0
t 1
2
Отсюда
имеем
t 4t 4
0 Нули числителя
:
2(
кратность четная)
lg x < 1;
t 1 2
Нули знам.:1(кратность нечетная)
lg x < lg10
t 2 0
+
+
т. к.
> 1, x >0, то
t 1
- a = 10 2
1 0 < x < 10
t 1
Ответ:
0; 10

17. IV. Решение логарифмических неравенств, содержащих переменную в основании логарифма

Теорема 1.
Если а > 0,
a ≠1, b> 0, c> 0,
1) неравенство logab > logac равносильно неравенству
(a -1)(b - c) > 0;
2) неравенство logab ≥ logac равносильно неравенству
(a -1)(b - c) ≥ 0;
3) неравенство logab < logac равносильно неравенству
(a -1)(b - c) < 0;
4) неравенство logab ≤ logac равносильно неравенству
(a -1)(b - c) ≤ 0;

18. Решение логарифмических неравенств, содержащих переменную в основании логарифма

Замечание- соглашение.
Для упрощения записей целесообразно
ввести символ v ,
понимая, что там, где стоит этот символ,
должен стоять один из знаков ≥, ≤,>либо<.
Тогда теорема 1 может быть
сформулирована более коротко: при всех
допустимых значениях a ,b и с неравенство
logab v logac равносильно (a -1)(b - c) v 0.
Если в процессе решения смысл неравенства
должен измениться, то пишется символ .

19.

Пример 1. Решите неравенство
logx+7(2x2-6x+8)≤logx+7(x2+x-2).
Решение: logx+7(2x2-6x+8) ≤ logx+7(x2+x-2)
x 7 1 2 x 2 6 x 8 x 2 x 2 0,
x 7 0 , x 7 1,
2 x 2 6 x 8 0,
x 2 x 2 0
x 6 x 5 x 2 0,
x 7, x 6,
x 2 x 1 0
x 6 x 2 7 x 10 0,
x 7, x 6,
2
x 3x 4 0,
x 2 x 1 0
6,
7 x -6
2 x 5.
-7 -6
x 3x 4 0
2
Так как D<0,то
x 3x 4 0
2
на x R
2
-2
5
1
Ответ: 7; 6 2;5 .
-7
-6
2
5

20. Следствие 1. При допустимых значениях a ,b и c неравенство logab - logac v 0 равносильно неравенству (a -1)(b - c) v 0

Следствие 1. При допустимых значениях a ,b
и c неравенство logab - logac v 0
(a -1)(b - c) v 0
Следствие 2. При допустимых значениях a и b
равносильно неравенству
неравенство logab
a
v
0 равносильно
неравенству ( -1)(b - 1) v 0
Пример .
Решите неравенство
log10-х(x2-5x+6) - log10-х(2x-4)≥0.
Решение:
10 x 1 x 2 5 x 6 2 x 4 0, x 9 x 2 x 5 0,
x 10, x 9,
x 9 x 5 x 2
10 x 0 , 10 x 1,
2
3 x 10, x 9,
x
2
x
3
0
,
x 5 x 6 0,
2 x 4 0
x 2
0,
5 x 9
Ответ: 5; 9

21.

1. Решите неравенство :
x
2
2 x 8 log x 5 2 x 7 0.
Ответ : 4; 3 2;4 .
2. Решите неравенство
log x x 3 log x 9 x
log x 1 x
0.
Ответ : 3;6

22.

Теорема 2.
При допустимых значениях a ,b , c, d неравенство
logab logcd v 0 равносильно неравенству
(a -1)(b - 1)(c-1)(d-1) v 0
2
x
log
log
x
1 0.
Решите неравенство:
1 x 1
x 2
x
Решение:
1 x
2
1
1
x
3
x
1 1 0
, 1 x 1
x 1 x 3
2
x x 1
0,
x x 1 x 3 x 0, x3 x 1
1 0, x 1,
x 2,
x
x 0, x 1,
x 3
x
x 1 0,
0,
x 1
x 2, x 3
x 2 0, x 2 1
2 x 3.
Ответ:
2;3 .

23.

Теорема 3.
При допустимых значениях a ,b , c неравенство
logab - logcb v 0 равносильно неравенству
(a -1)(b - 1)(c-1)(c-a) v 0.
Решите неравенство:
log x x 1 log x 1 x 1 0.
Решение:
x 1 x 1 1 x 1 1 x 1 x 0,
x x 1 x 2 0,
x 0, x 1,
1 x 2.
x 1
x
1
0
,
x 1 0, x 1 1
Ответ: 1;2 .

24.

Домашнее
задание.
1) Разобрать приёмы решений логарифмических
уравнений и неравенств по лекции.
2) Никольский 10 кл.
I. № 6.33 – 6. 34, 6.37(а, б), 6.38(а),6.41(a,г)
II. № 6.37(а, б), 6. 39(в, г), 6.41(б, в), 6.42(в, г).