Похожие презентации:
Критические точки функции, максимумы и миниумы
1.
2. Эпиграф.
“При изучении наук примеры неменее поучительны, нежели
правила”.
“Примеры учат больше, чем
теория”.
( И. Ньютон , М. Ломоносов )
3.
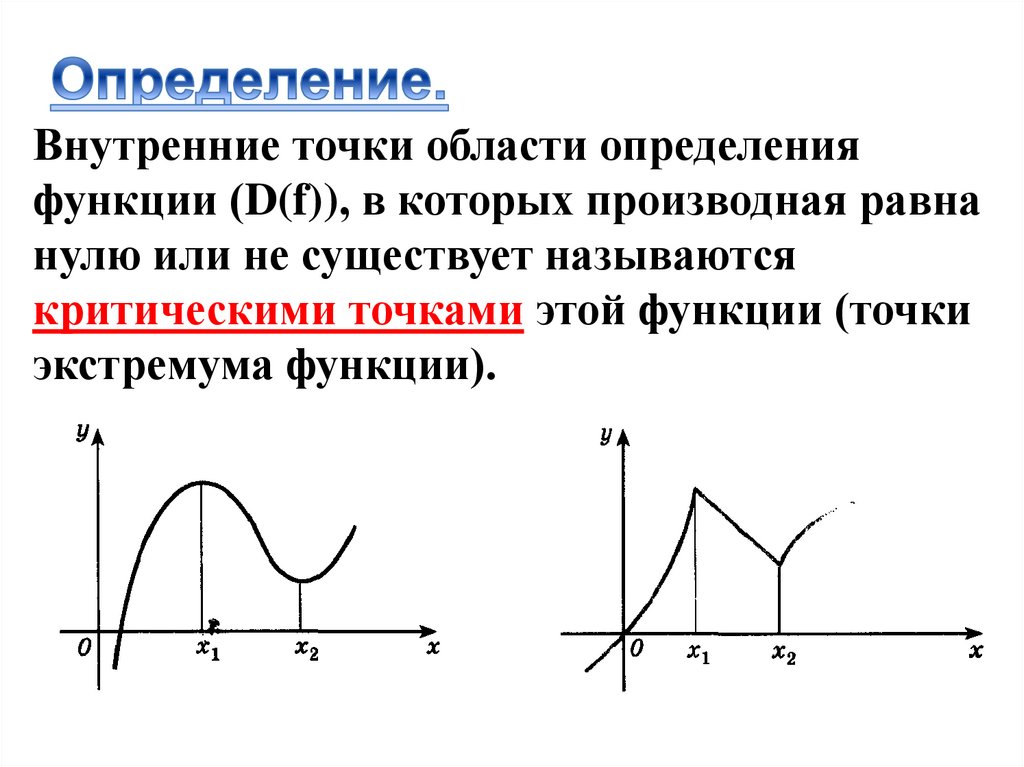
Внутренние точки области определенияфункции (D(f)), в которых производная равна
нулю или не существует называются
критическими точками этой функции (точки
экстремума функции).
4.
5.
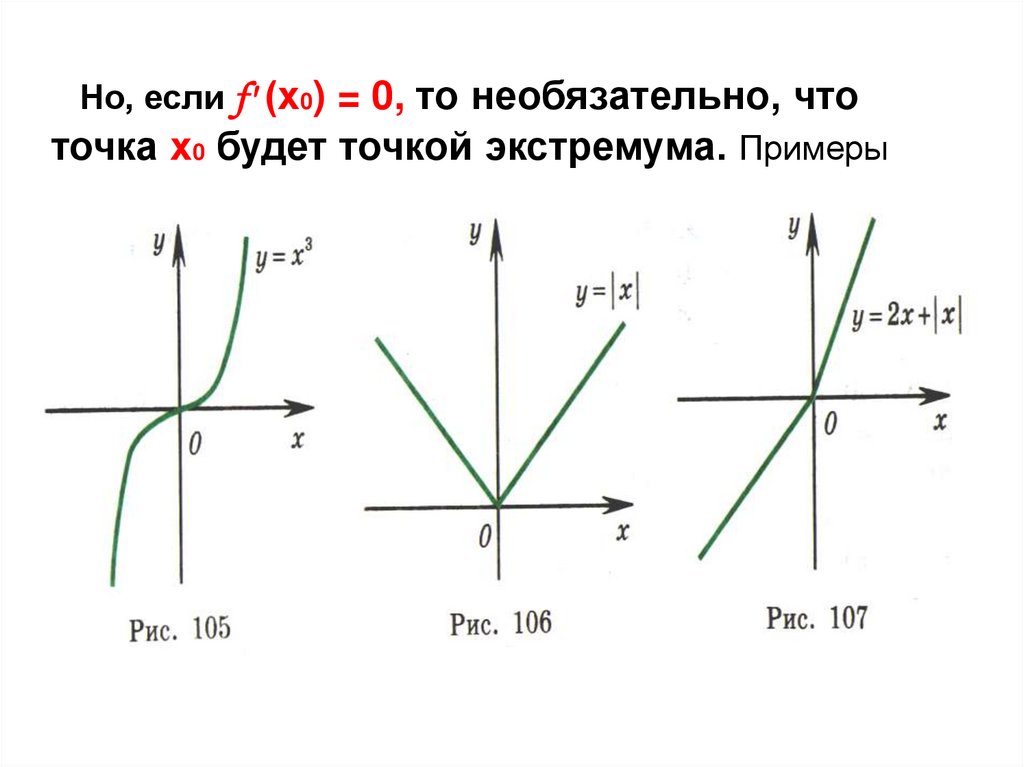
Но, если f' (х0) = 0, то необязательно, чтоточка х0 будет точкой экстремума. Примеры
6.
f(x)f′(x)
a
-
+
x0
max
b x
7.
f(x)f′(x)
a
+
x0
min
b x
8.
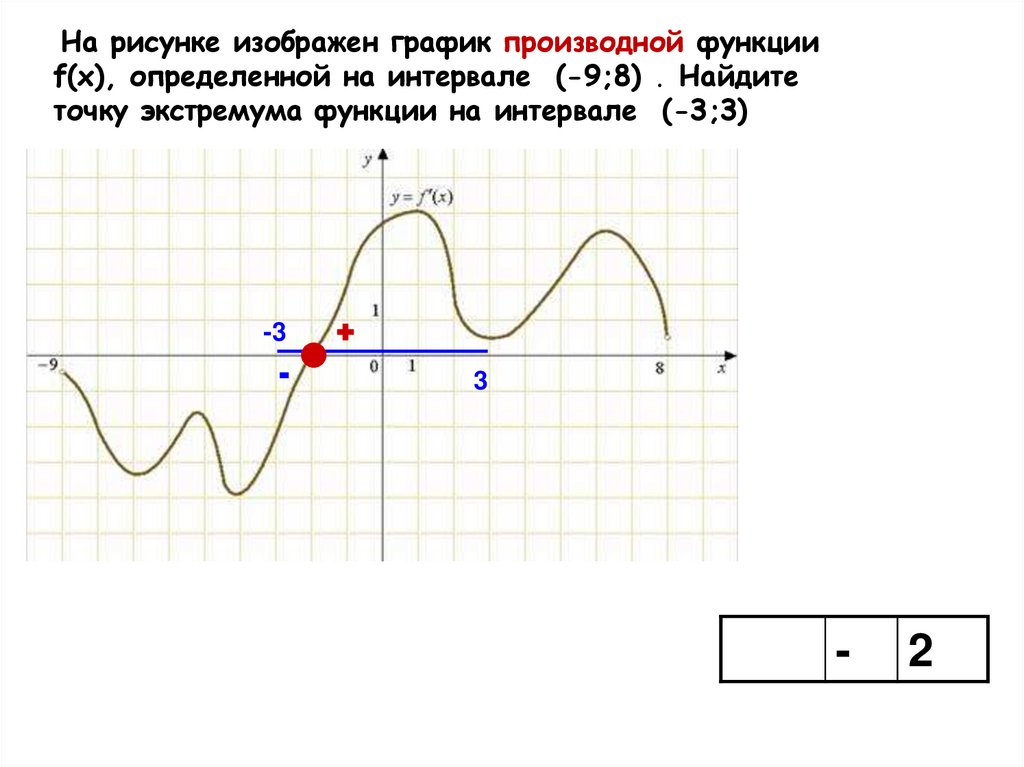
На рисунке изображен график производной функцииf(x), определенной на интервале (-9;8) . Найдите
точку экстремума функции на интервале (-3;3)
-3
-
+
3
-
2
9.
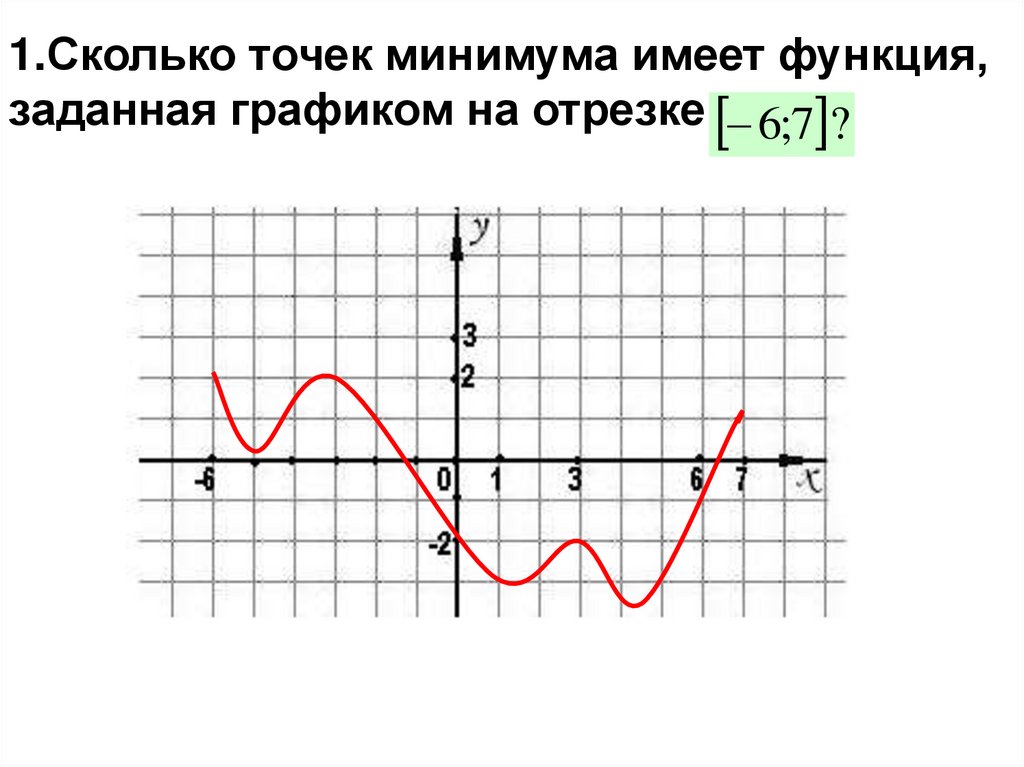
1.Сколько точек минимума имеет функция,заданная графиком на отрезке 6;7 ?
10.
На рисунке изображен график функции y=f(x) , определенной наинтервале (-3;11) . Найдите сумму точек экстремума функции.
-2+1+3+4+5+8+10=…
-2
3. 4
1
5
8
10
2 9






 Математика
Математика








