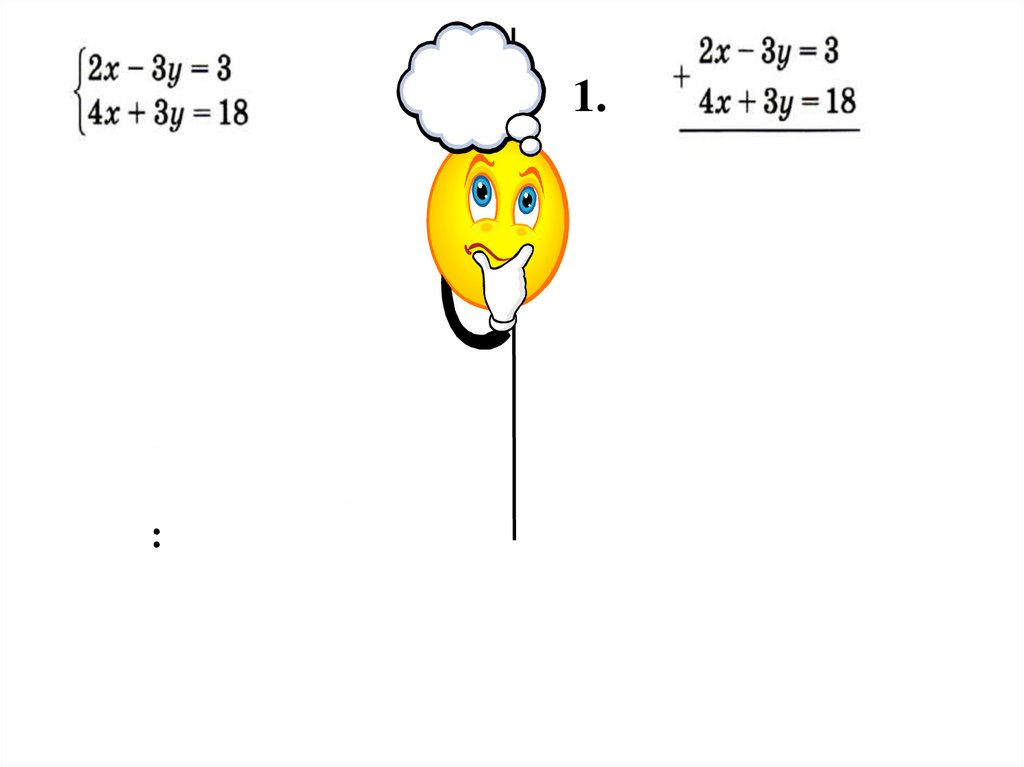Похожие презентации:
Решение систем уравнений способом сложения
1. решение систем уравнений способом сложения
РЕШЕНИЕ СИСТЕМУРАВНЕНИЙ
СПОСОБОМ
СЛОЖЕНИЯ
2.
3.
Определения:Системой уравнений называется некоторое
количество уравнений, объединенных фигурной
скобкой. Фигурная скобка означает, что все
уравнения должны выполняться одновременно.
Пара чисел, которая является решением каждого
из уравнений, входящих в систему, называют
решением системы.(х;у)
Решением системы уравнений с двумя
переменными называется пара значений
переменных, обращающая каждое уравнение
системы в верное равенство.
Решить систему уравнений - это значит найти все
её решения или убедиться в том, что их нет.
4.
1.2.
Отве:
5.
1.2.
+
6.
7.
Способ СЛОЖЕНИЯ8.
1.2.
+
9.
Устная работа1. Выясните, является ли пара чисел (–1; 1) решением системы уравнений:
x y 2,
3
y
3;
а)
да
2 x 2,
б) x y 1;
нет
3x y 4,
в) x y 0;
нет
2 x 3 y 1,
г) x y 2.
да
10.
Устная работа2. Решите систему уравнений:
a b 3,
а) a b 1;
(-1; -2)
2 x y 4,
б) 3 x y 1;
(1; -2)
a 4b 2,
в) a 3b 1; ;
(-2; 1)
2 x y 2,
г) 5 x y 5.
(1; 0)
11.
3x 2 y 9,3
x
2
y
5
Решим
систему
уравнений:
1) Нельзя подобрать два таких числа, подстановка
которых в одинаковые выражения дает разные значения.
2) При построении получаются две параллельные
прямые, то есть система не имеет решений.
3) Если найти разность левых и правых частей уравнений,
то получим равенство 0 = 4, которое является неверным, что
говорит о том, что система решений не имеет.
12.
13.
Решим систему уравнений:4x – 2y = 6
2x – y = 3
/:2
2 x y 3,
2 x y 3.
1) Очевидно, что какие бы пары чисел, являющихся решениями первого
уравнения, мы ни нашли, они будут служить и решениями второго
уравнения, поскольку эти уравнения одинаковые.
2) С геометрической точки зрения уравнения, входящие в систему,
задают одну и ту же прямую (то есть прямые совпадают), поэтому
система имеет бесконечно много решений.
3) Если
найти разность левых и правых частей уравнений,
то получим числовое равенство 0 = 0, которое является
верным.
14.
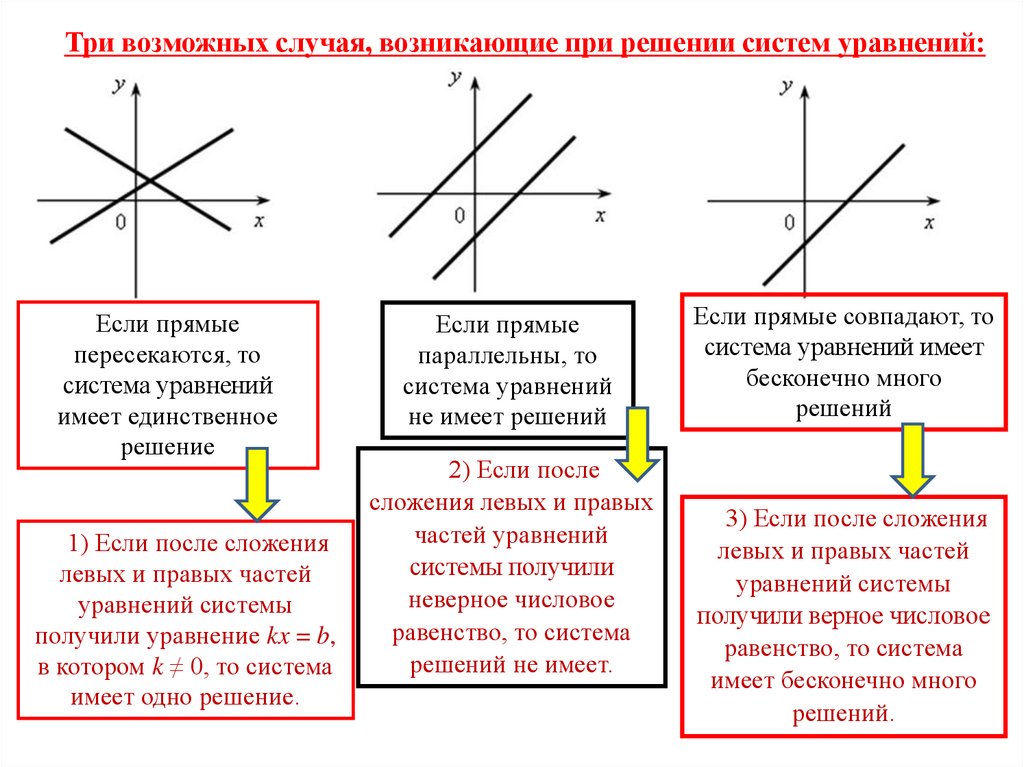
Три возможных случая, возникающие при решении систем уравнений:Если прямые
пересекаются, то
система уравнений
имеет единственное
решение
1) Если после сложения
левых и правых частей
уравнений системы
получили уравнение kx = b,
в котором k ≠ 0, то система
имеет одно решение.
Если прямые
параллельны, то
система уравнений
не имеет решений
2) Если после
сложения левых и правых
частей уравнений
системы получили
неверное числовое
равенство, то система
решений не имеет.
Если прямые совпадают, то
система уравнений имеет
бесконечно много
решений
3) Если после сложения
левых и правых частей
уравнений системы
получили верное числовое
равенство, то система
имеет бесконечно много
решений.
15.
С помощью графиков выясните, сколько решений имеетсистема уравнений:
3x y 2,
3
x
y
4;
а)
3x y 4,
2
y
6
x
8;
г)
2 x y 1,
4
x
2
y
3;
б)
2 x 4,
3
y
3;
д)
4 x 2 y 1,
y
3;
в)
x 1,
x
y
3.
е)
16.
Не выполняя построения, определите, как расположеныграфики уравнений системы, и сделайте вывод относительно
числа ее решений:
y 2 x 1,
y
3
x
5;
а)
y x 5,
y
5
x
;
в)
y 4 x 7,
y
4
x
1;
б)
y 2 3x,
y
3
x
2.
г)
17.
Решите систему уравнений:3a 4b 7,
5
a
3
b
8;
а)
2 y 5 z 1,
4
y
10
z
3;
б)
5a 7b 2,
10
a
14
b
4;
в)
15m 12n 11,
4
n
5
m
3.
г)
18.
ЗАДАЧА, ПРИВОДЯЩАЯ КПОНЯТИЮ
«СИСТЕМА УРАВНЕНИЙ»
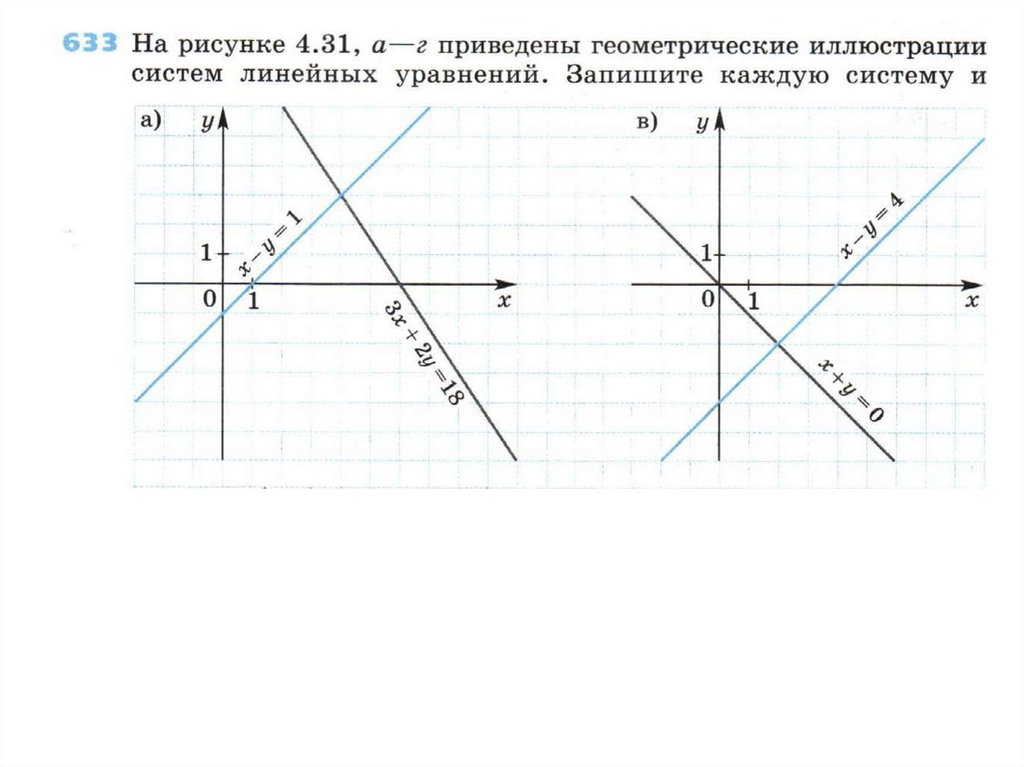
№ 633 (а, в),
№634,
Домашнее
№ 636 (а, в, д),
задание
№ 637 (а).
№ 633 (б, г),
№ 638 (а, б).
№ 635,
№636 (б, г, е),
№637 (б).
19.
20.
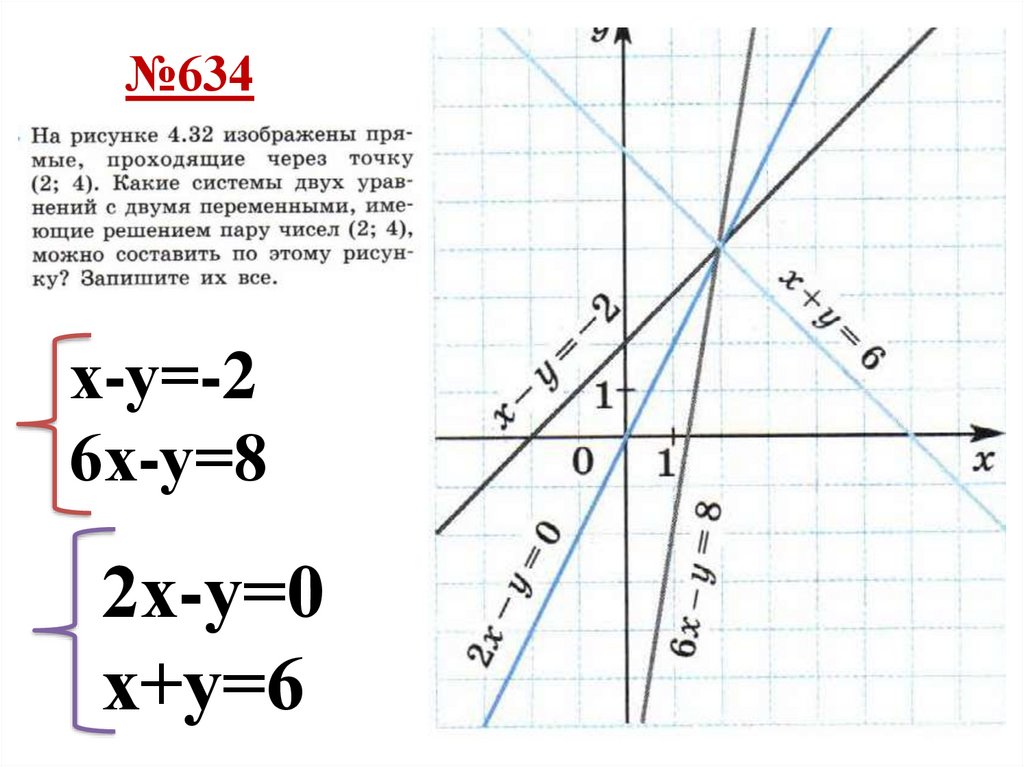
№634х-у=-2
6х-у=8
2х-у=0
х+у=6
21.
22.
Подведём итоги– Как алгебраически найти координаты точки
пересечения двух прямых?
– Что называется решением системы линейных
уравнений?
– В чем заключается способ сложения при решении систем
уравнений?
– Сколько решений может иметь система линейных
уравнений?
– Как графически определить количество решений
системы уравнений?
– Как определить с помощью способа сложения, что
система уравнений не имеет решений?
- Имеет бесконечно много решений?