Лемма. Параллельность трёх прямых

1.

2.

Лемма
Если одна из двух параллельных
прямых пересекает данную плоскость,
то и другая прямая пересекает данную
плоскость

3.

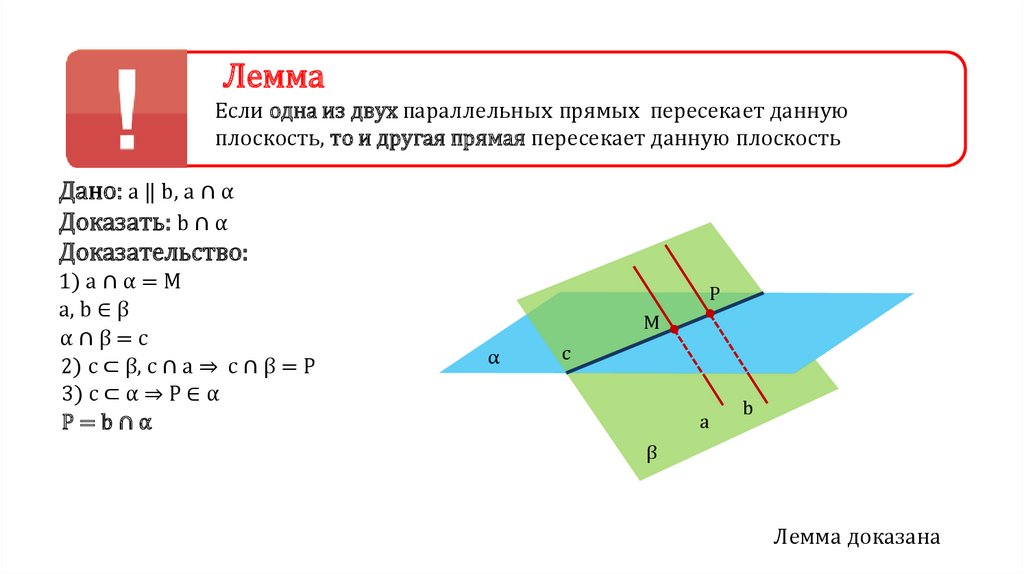
Лемма
Если одна из двух параллельных прямых пересекает данную
плоскость, то и другая прямая пересекает данную плоскость
Дано: a ‖ b, a ∩ α
Доказать: b ∩ α
Доказательство:
1) a ∩ α = M
a, b ∈ β
α∩β=c
2) c ⊂ β, c ∩ a ⇒ c ∩ β = P
3) c ⊂ α ⇒ P ∈ α
P=b∩α
P
M
α
c
a
b
β
Лемма доказана

4.

Теорема
Если две прямые параллельны
третьей прямой, то они
параллельны

5.

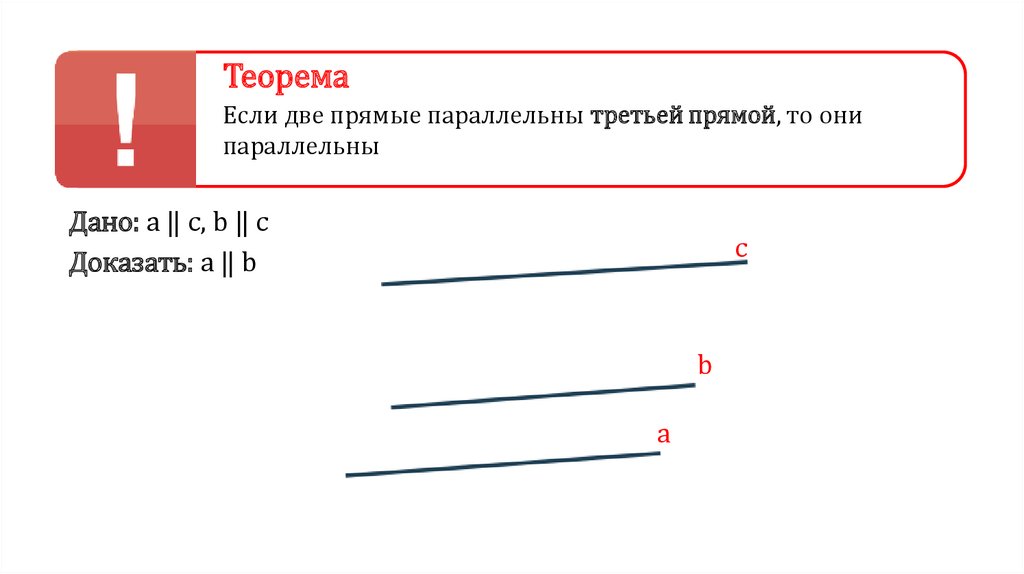
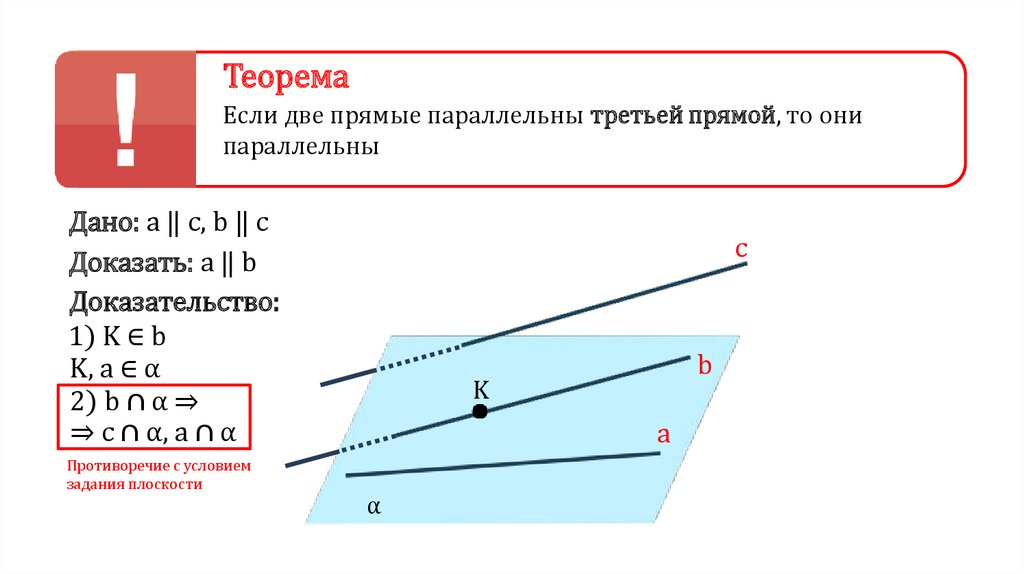
Теорема
Если две прямые параллельны третьей прямой, то они
параллельны
Дано: a ‖ c, b ‖ c
Доказать: a ‖ b
с
b
a

6.

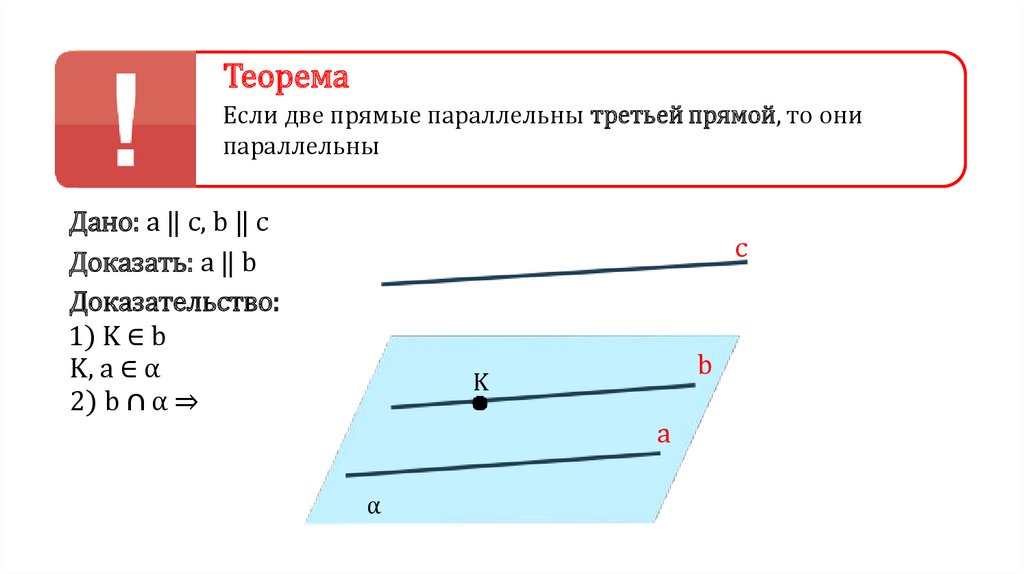
Теорема
Если две прямые параллельны третьей прямой, то они
параллельны
Дано: a ‖ c, b ‖ c
Доказать: a ‖ b
Доказательство:
1) K ∈ b
K, a ∈ α
2) b ∩ α ⇒
с
b
K
a
α

7.

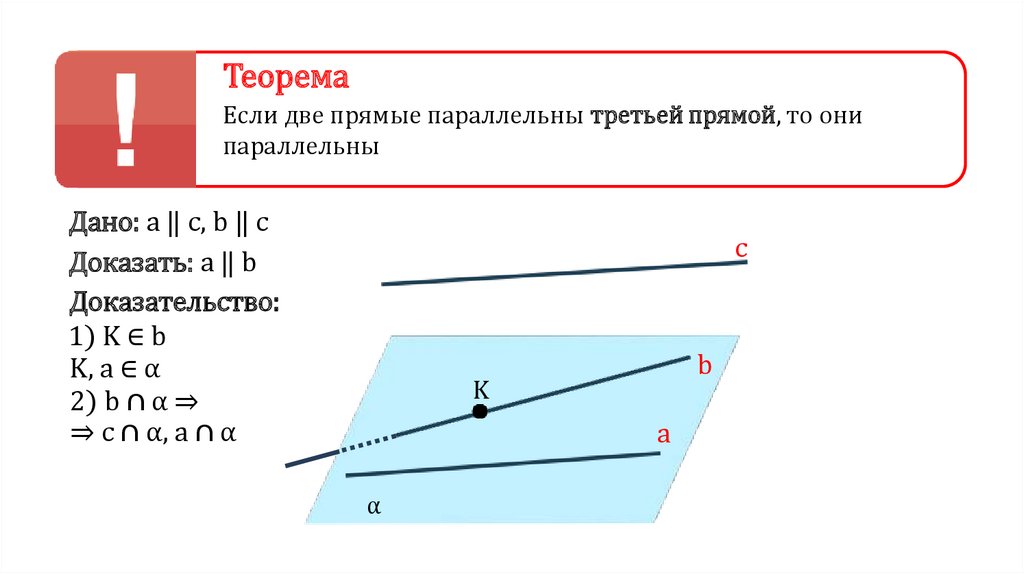
Теорема
Если две прямые параллельны третьей прямой, то они
параллельны
Дано: a ‖ c, b ‖ c
Доказать: a ‖ b
Доказательство:
1) K ∈ b
K, a ∈ α
2) b ∩ α ⇒
⇒ c ∩ α, a ∩ α
с
b
K
a
α

8.

Теорема
Если две прямые параллельны третьей прямой, то они
параллельны
Дано: a ‖ c, b ‖ c
Доказать: a ‖ b
Доказательство:
1) K ∈ b
K, a ∈ α
2) b ∩ α ⇒
⇒ c ∩ α, a ∩ α
с
b
K
a
Противоречие с условием
задания плоскости
α

9.

Теорема
Если две прямые параллельны третьей прямой, то они
параллельны
Дано: a ‖ c, b ‖ c
Доказать: a ‖ b
Доказательство:
1) K ∈ b
K, a ∈ α
2) b ∩ α ⇒
⇒ c ∩ α, a ∩ α
с
b
K
a
Противоречие с условием
задания плоскости
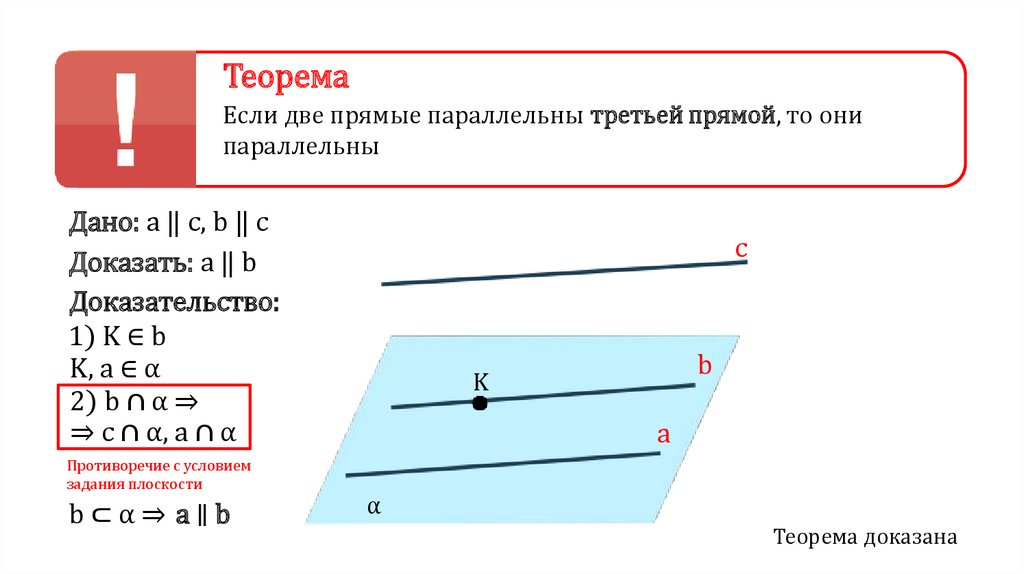
b⊂α⇒ a∥b
α
Теорема доказана

10.

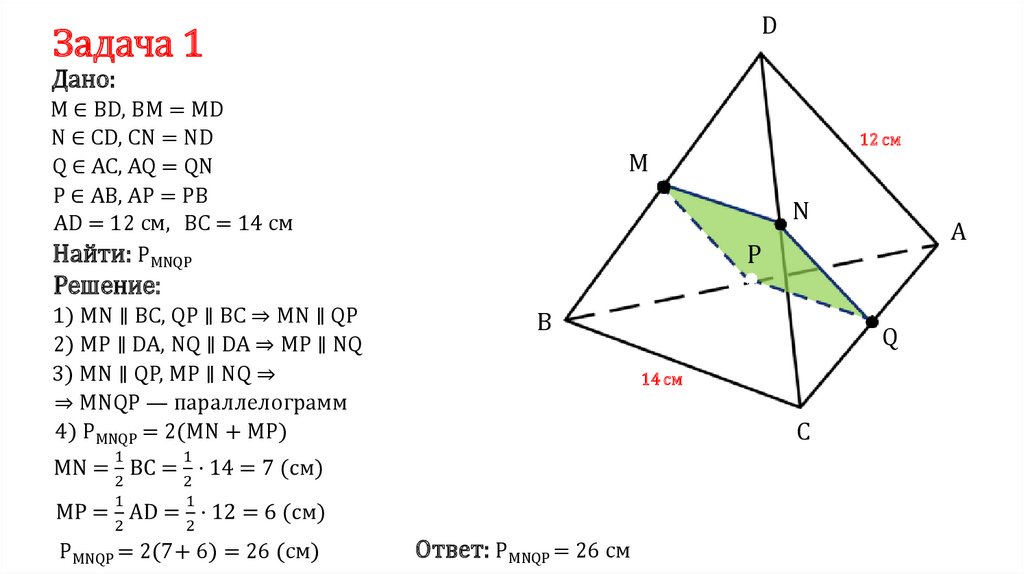
D
Задача 1
Дано:
М ∈ BD, BM = MD
N ∈ CD, CN = ND
Q ∈ АС, AQ = QN
P ∈ АВ, AP = PB
АD = 12 см, ВС = 14 см
Найти: PMNQP
12 см
M
N
А
P
Решение:
1) MN ∥ ВС, QР ∥ ВС ⇒ MN ∥ QР
2) MP ∥ DA, NQ ∥ DA ⇒ MP ∥ NQ
3) MN ∥ QР, MP ∥ NQ ⇒
⇒ MNQP — параллелограмм
4) PMNQP = 2(MN + МР)
PMNQP = 2(7+ 6) = 26 (см)
В
Q
14 см
С
Ответ: PMNQP = 26 см

11.

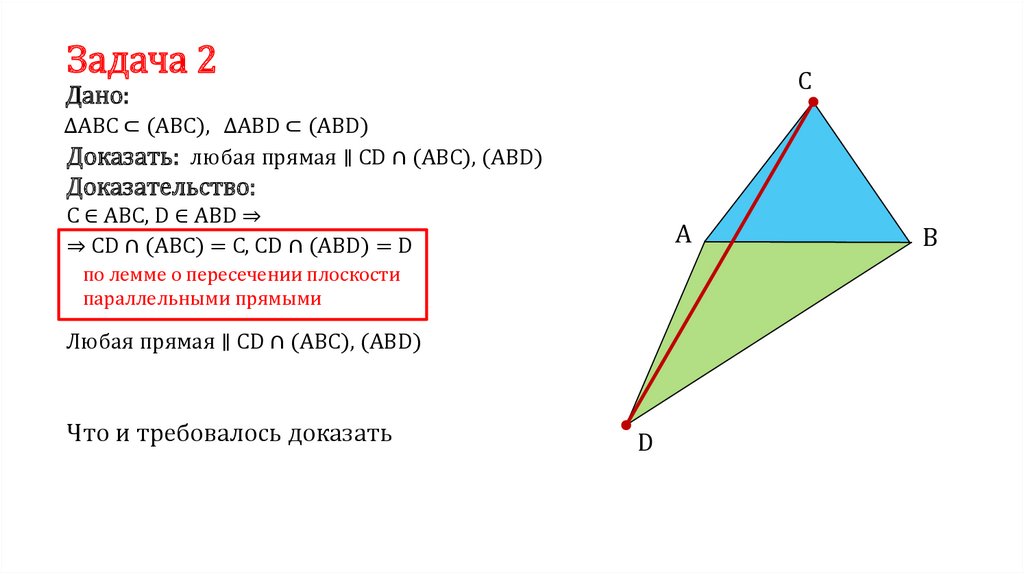
Задача 2
C
Дано:
ΔАВС ⊂ (АВС), ΔАВD ⊂ (АВD)
Доказать: любая прямая ∥ СD ∩ (АВС), (ABD)
Доказательство:
С ∈ АВС, D ∈ ABD ⇒
⇒ CD ∩ (ABC) = C, СD ∩ (ABD) = D
A
по лемме о пересечении плоскости
параллельными прямыми
Любая прямая ∥ СD ∩ (АВС), (ABD)
Что и требовалось доказать
D
B