Похожие презентации:
Внутренняя энергия идеального газа
1. ВНУТРЕННЯЯ ЭНЕРГИЯ ИДЕАЛЬНОГО ГАЗА
• В идеальном газе молекулы невзаимодействуют между собой
• Внутренняя энергия идеального газа –
это кинетическая энергия молекул
• Для 1 молекулы
i
• Для 1 моля
E kT
2
i
i
U m kT N A RT
2
2
2.
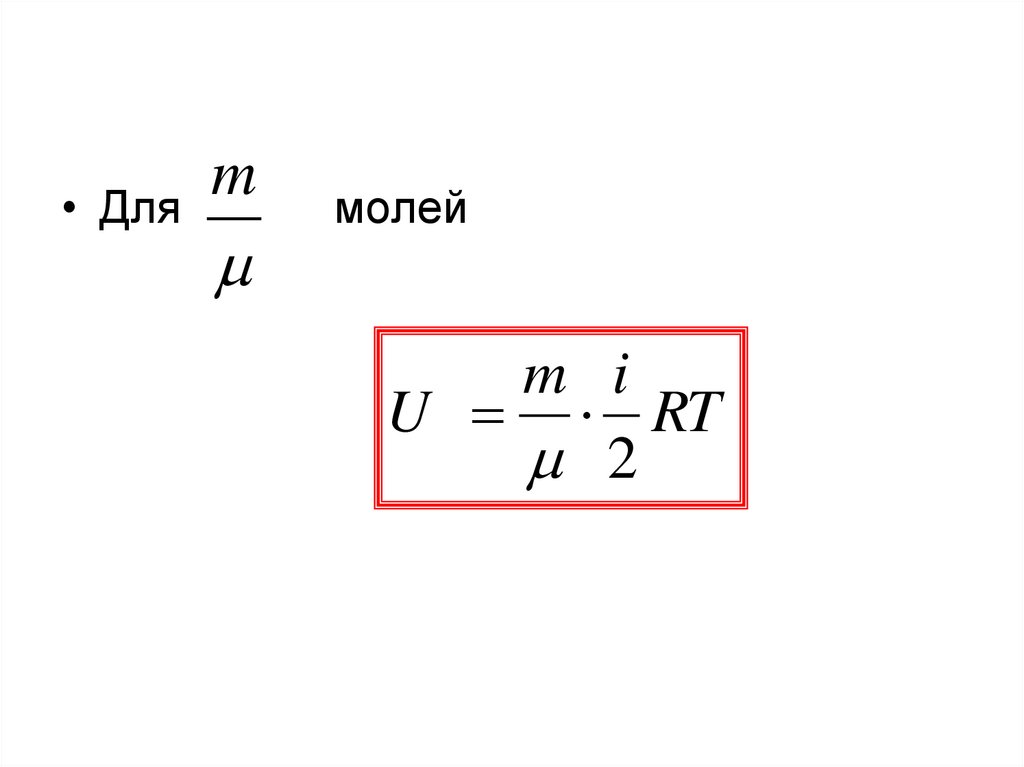
• Дляm
молей
m i
U RT
2
3. Пример
• Внутренняя энергия 1 моляодноатомного газа при Т=300 К
m i
U RT
2
i 3
m
3
U 1 8,31 300 3740 Дж
2
1
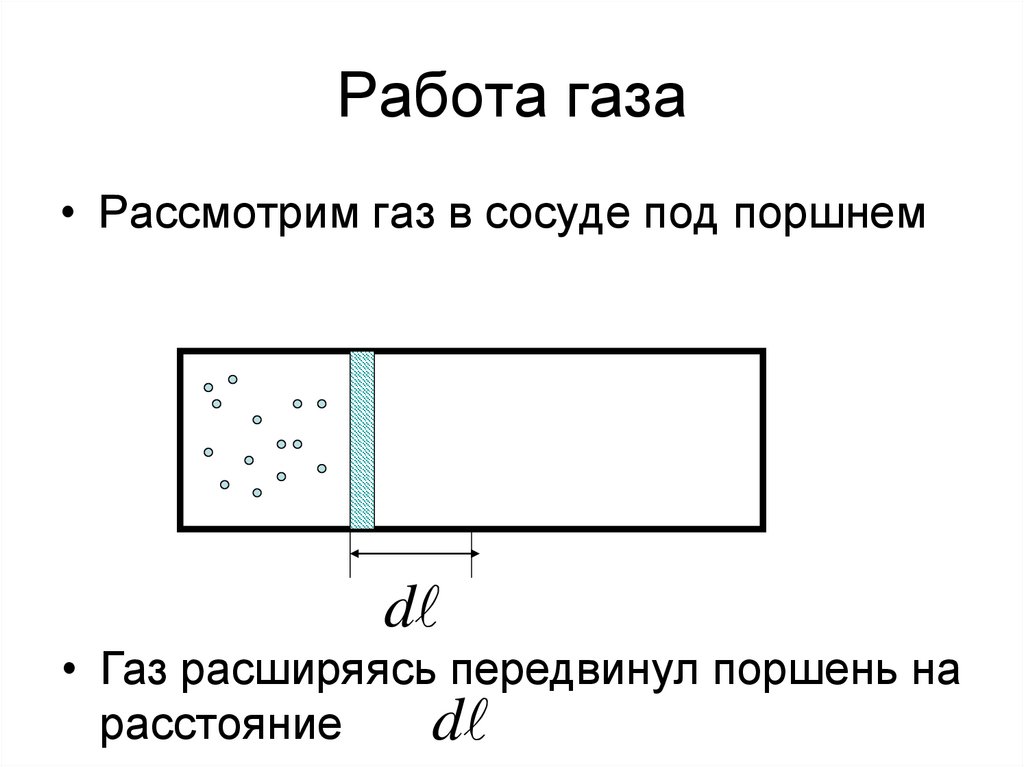
4. Работа газа
• Рассмотрим газ в сосуде под поршнемd
• Газ расширяясь передвинул поршень на
расстояние
d
5.
• РаботаA F d p S d p dV
• S – площадь поперечного сечения
• dV – объем, на который расширился газ
A p dV
6.
• Полная работаA
V2
p
dV
V1
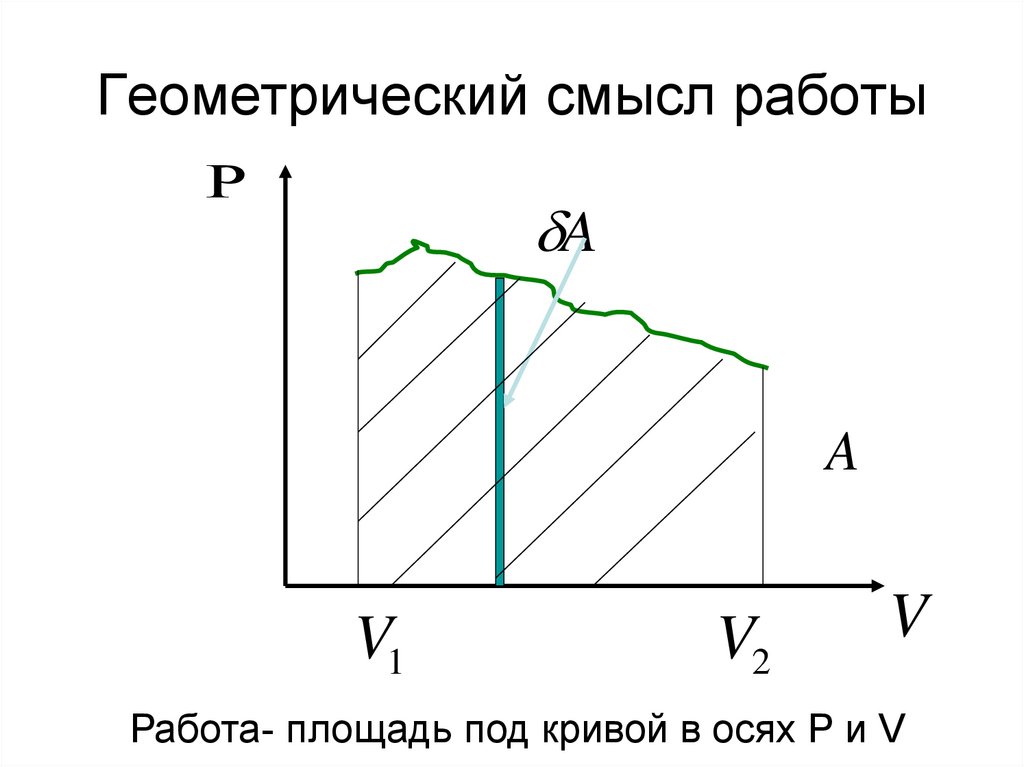
7. Геометрический смысл работы
AA
V1
V2
V
Работа- площадь под кривой в осях Р и V
8.
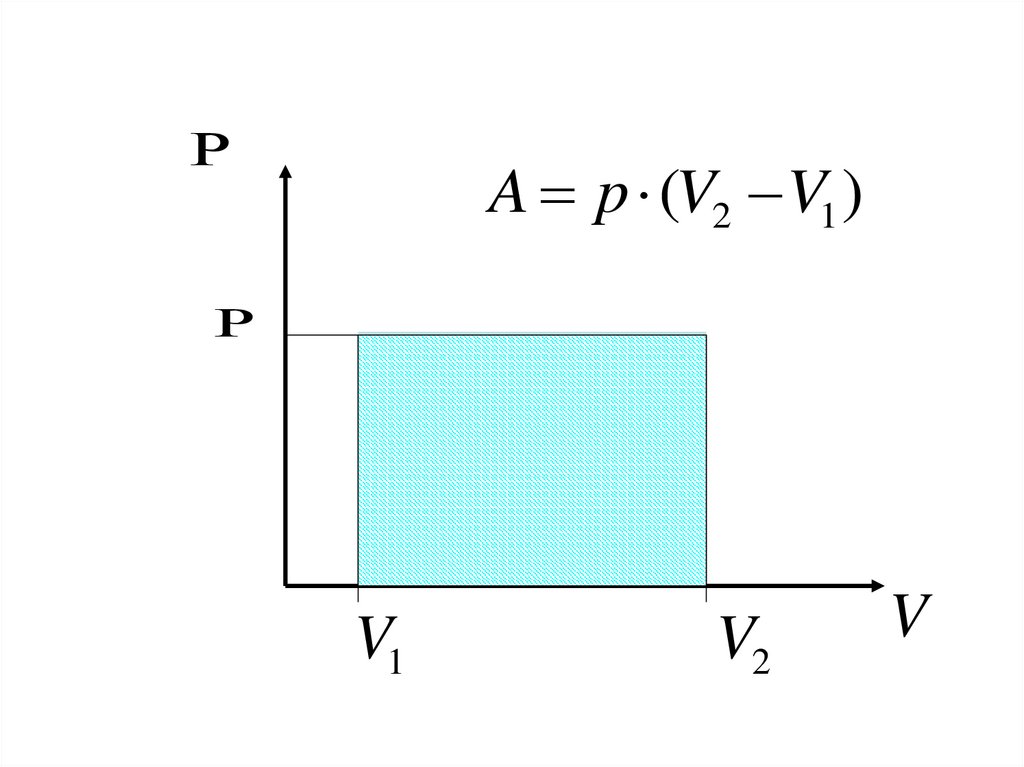
A p (V2 V1 )V1
V2
V
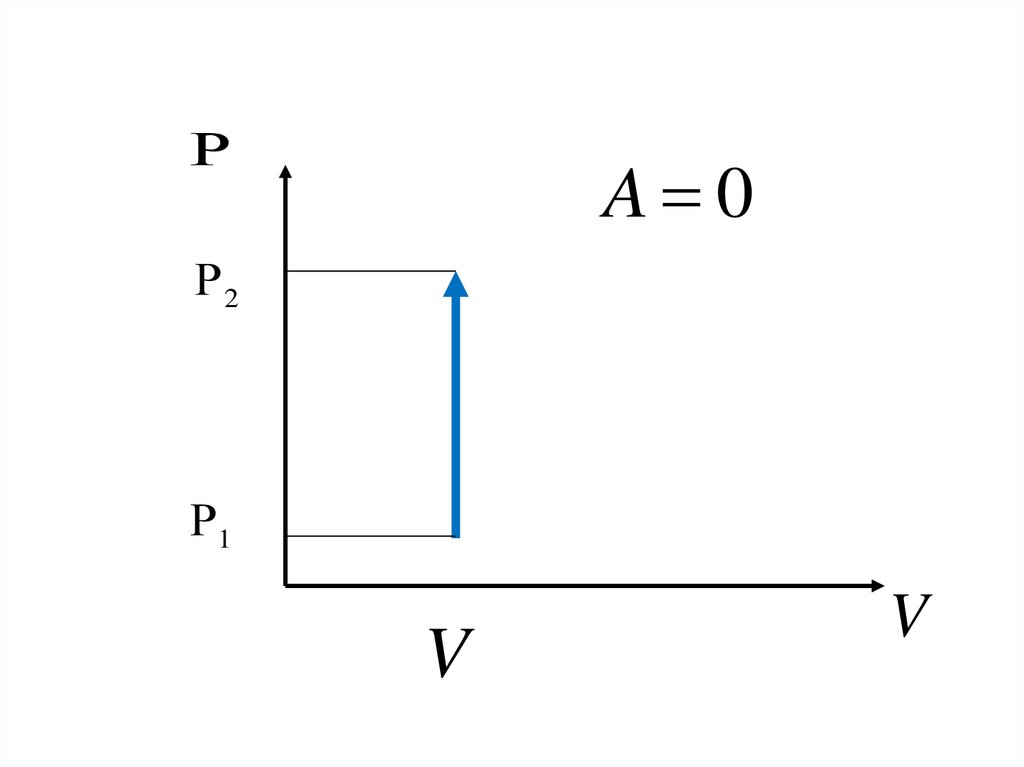
9.
A 02
1
V
V
10. Первое начало термодинамики
• Внутреннюю энергию газа можно изменить• 1) совершая работу
• При движении поршня меняется давление ,
следовательно меняется температура,
меняется внутренняя энергия
11.
• 2) Внутреннюю энергию можноизменить нагревая или охлаждая газ
• При этом выполняется закон
сохранения энергии ( 1 начало
термодинамики)
• Теплота сообщенная системе (δQ)
расходуется на изменение ее
внутренней энергии (∆U) и на
совершение работы против внешних
сил (δА)
12.
Q dU AQ 0
если она подводится к газу
A 0
если газ совершает работу
изменение внутренней энергии
не зависит от способа перехода из
одного состояния в другое
dU
13. Теплоемкость
• Удельная теплоемкость – количествотеплоты, необходимое для нагревания
1 кг вещества на 1 градус
Дж
Q
C
C
mdT
кг К
• Молярная теплоемкость – количество
теплоты, необходимое для нагревания
1 моля вещества на 1 градус
Q
Дж
cm C
cm
cm
dT
моль К
14. Теплоемкость при постоянном объеме и при постоянном давлении
• Первое начало т/д для 1 моляQm dU m Am
cm dT dU m pdVm
• Если Vm=const, то
cV dT dU m
pdVm 0
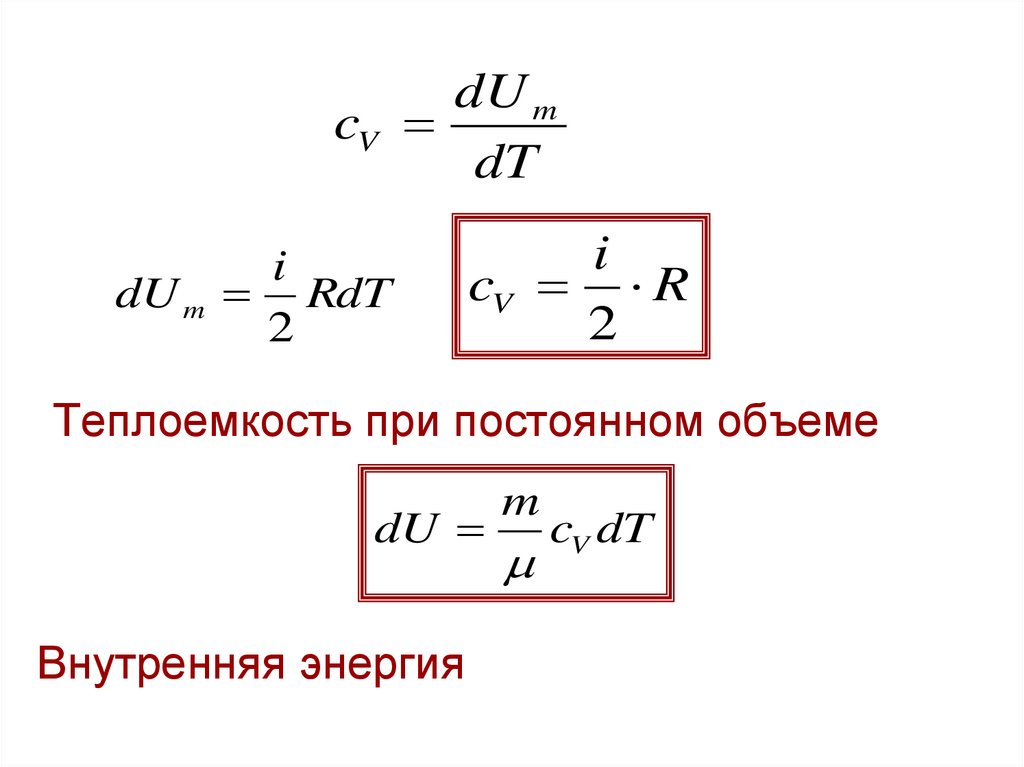
15.
dU mcV
dT
dU m
i
RdT
2
i
cV R
2
Теплоемкость при постоянном объеме
dU
Внутренняя энергия
m
cV dT
16.
• Если p=const,c p dT dU m pdVm
dU m
dVm
cp
p
dT
dT
dU m
dV
m
cV
p
R
dT
dT
c p cV R
Уравнение Майера
17.
icV R
2
i
c p cV R R R i 2 R
2
2
i 2
cp
R
2
18.
• Важно соотношениеi 2
R
2
i
R
2
i 2
i
cp
cV
i 2
i
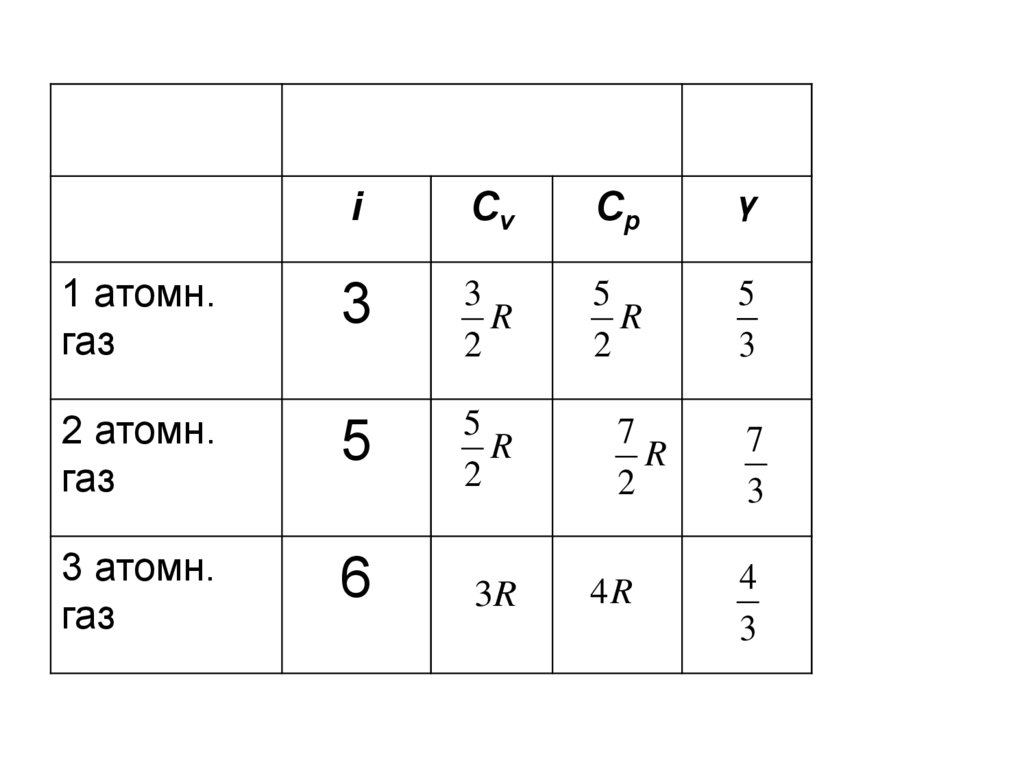
19.
iCv
Cp
γ
3
3
R
2
5
R
2
5
3
2 атомн.
газ
5
5
R
2
3 атомн.
газ
6
3R
1 атомн.
газ
7
R
2
4R
7
3
4
3
20. Применение первого начала термодинамики к изопроцессам
Изохорный процесс V=constQ dU A
A 0
Q dU
m
Q cV dT
21.
Изобарный процесс p=constQ dU A
A pdV
m
Q p c p dT
m
m
c p dT cV dT pdV
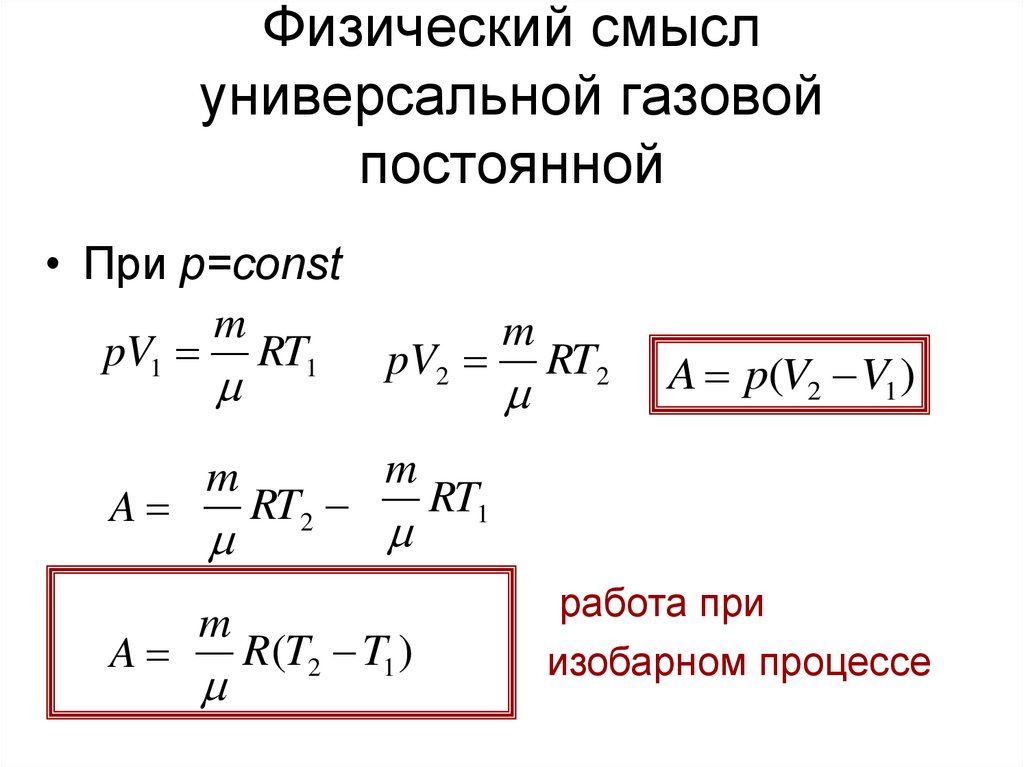
22. Физический смысл универсальной газовой постоянной
• При p=constm
pV1 RT1
A
m
A
m
RT2
pV2
m
R(T2 T1 )
m
RT2
A p(V2 V1 )
RT1
работа при
изобарном процессе
23.
• ЕслиT2 T1 1
m
1
A R
• R- это работа изобарного расширения 1
моля газа при нагревании его на 1
градус
24.
Изотермический процессТ=const
Q dU A
U 0
Q A
A
V2
p dV
V1
pV
m
RT
m RT
p
V
25.
V2m RT
A
dV
V
V1
V2
m
dV
RT
V
V1
m
V2
RT ln
A
V1
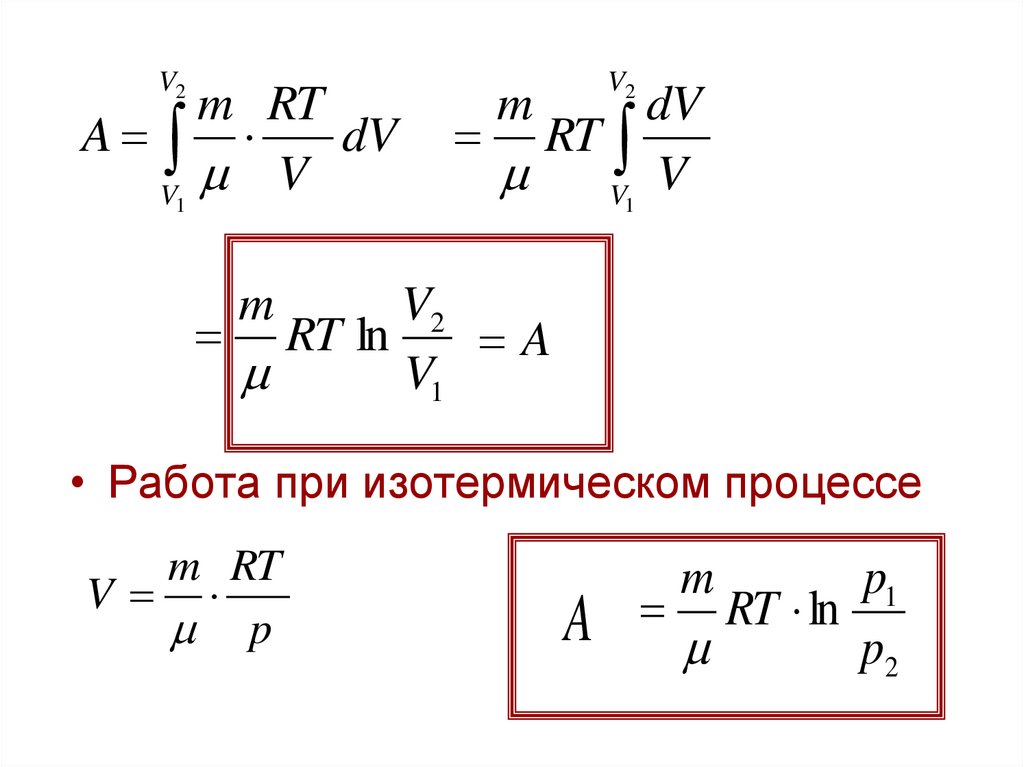
• Работа при изотермическом процессе
m RT
V
p
A
m
p1
RT ln
p2
26.
• Чтобы при изотермическом процессетемпература газа не понижалась, к
нему необходимо подводить тепло,
равное работе расширения газа
27. Адиабатный процесс
• Процесс, при котором отсутствуеттеплообмен с окружающей средой
Q dU A
Q 0
dU A
• Работа совершается за счет изменения
внутренней энергии газа
28. Уравнение Пуассона
dU AA
pV
m
m
pdV
cV dT
RT
dpV pdV
m
RdT
m
cV dT
29.
mRdT
dpV pdV
m
pdV
cV dT
dpV pdV
R
pdV
cV
dpV
1 1
pdV
c p cV
cV
dpV
pdV
30.
dpdV
p
V
p2
V2
ln
ln
p1
V1
p2V2 p1V1
p2
V1
ln
ln
p1
V2
pV const
Уравнение адиабаты ( уравнение Пуассона)
31.
TV1
1
const
P T const
32.
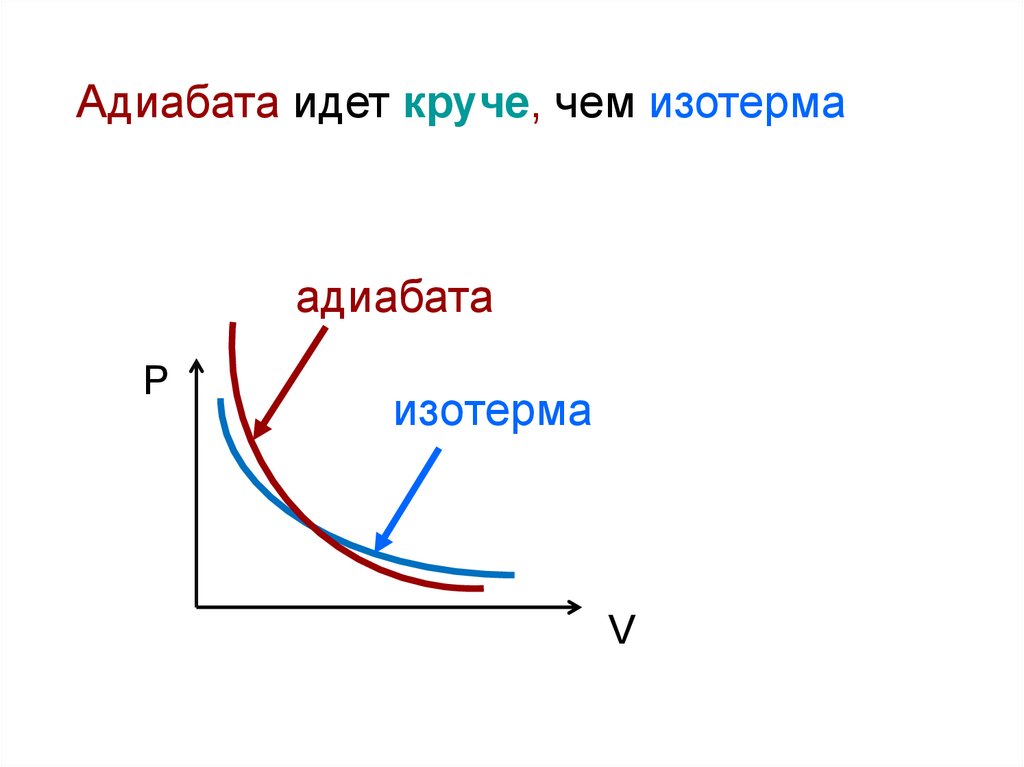
Адиабата идет круче, чем изотермаадиабата
P
изотерма
V
33.
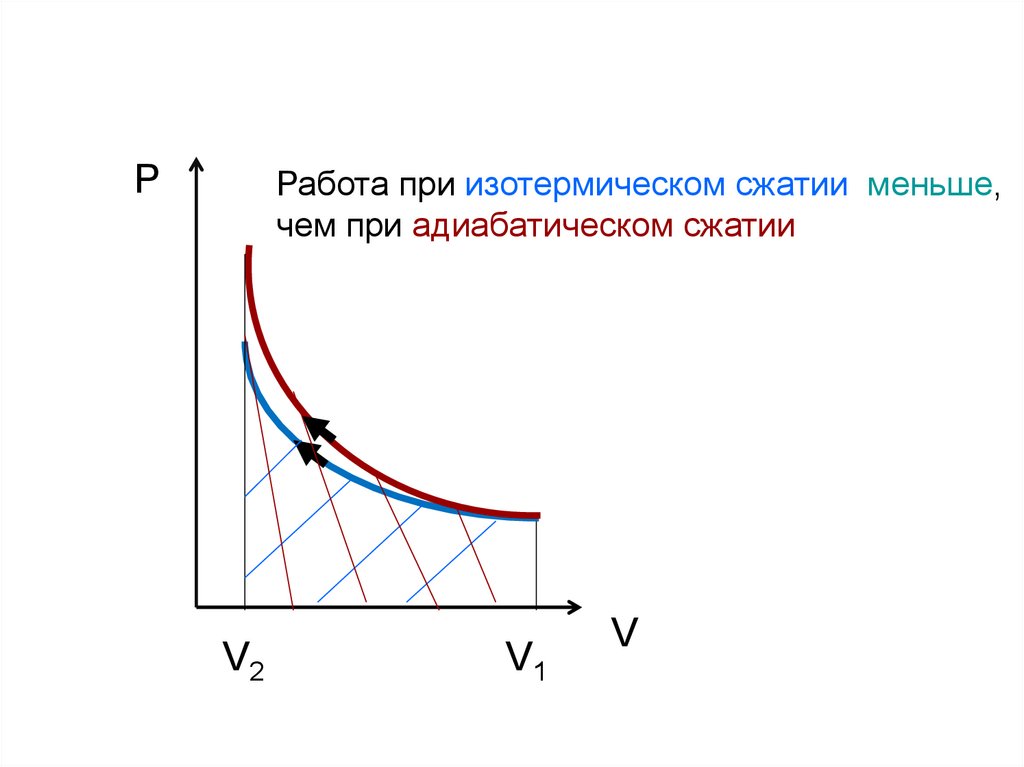
PРабота при изотермическом сжатии меньше,
чем при адиабатическом сжатии
V2
V1
V
34.
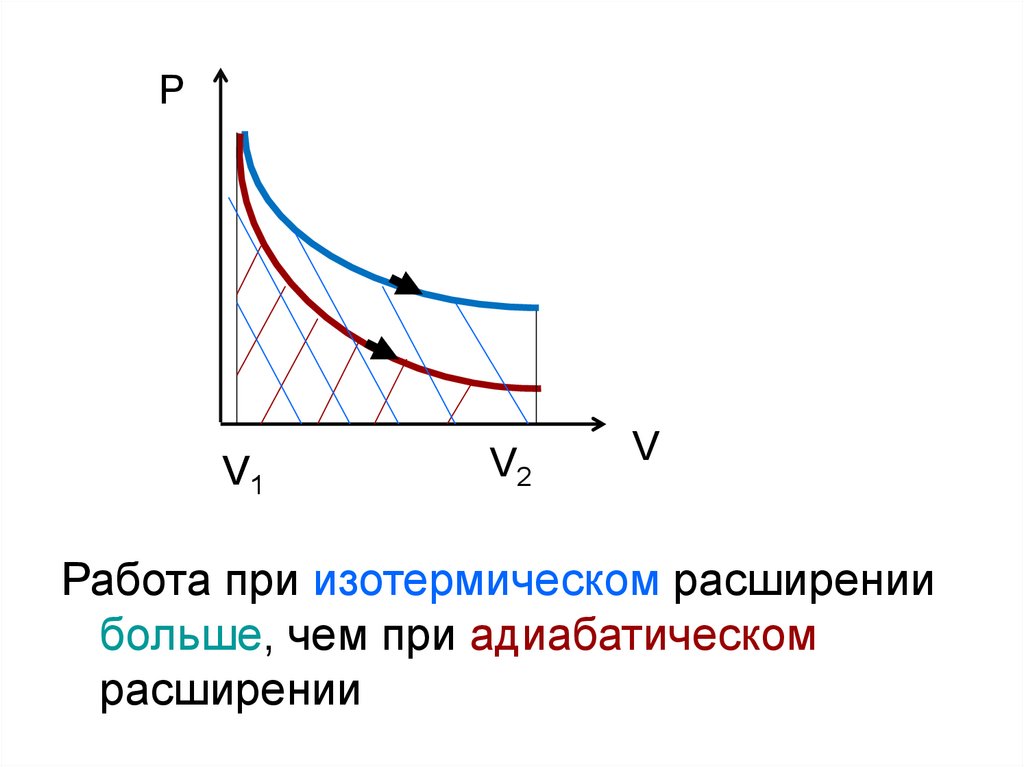
PV1
V2
V
Работа при изотермическом расширении
больше, чем при адиабатическом
расширении
35. Работа газа при адиабатическом расширении
AT2
A
T1
m
m
cV dT
cV dT
A
m
m
cV (T2 T1 )
cV (T1 T2 )
36.
V1R
A
T1 1
1 V2
m
p1V1 V1
A
1
11 V2
1
1



















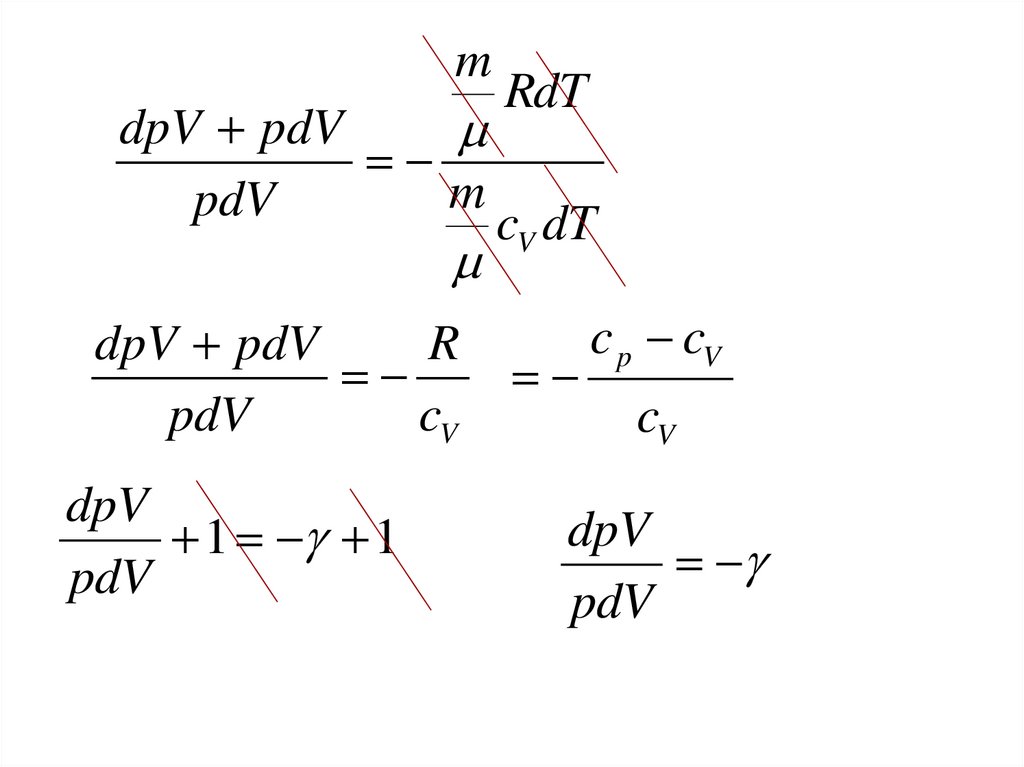




 Физика
Физика