Теплоемкость идеального газа. Изопроцессы

1.

Теплоемкость
идеального газа
Изопроцессы

2.

Внутренняя энергия и теплоемкость идеального газа
Средняя энергия одной молекулы
Т.к. молекулы идеального газа на
расстоянии не взаимодействую,
внутренняя энергия газа равна сумме
внутренних энергий всех молекул
i
U kT
2
Для 1 моля, где N=NA
i
i
U N AU N A kT RT
2
2
Внутренняя энергия произвольной массы m
m
mi
U Um
RT
2
Внутренняя энергия
идеального газа зависит
только от температуры

3.

Теплоемкость
Теплоёмкость тела величина, равная количеству
теплоты, которую надо сообщить телу, чтобы
повысить его температуру на 1 градус для
нагревания этого тела на один градус:
dQ cmdT
если m=1кг
dQ
C
dT
Дж
К

4.

Удельная
теплоёмкость
(с)
–
количество теплоты, необходимое для
нагревания единицы массы вещества на один
Дж
градус.
[с] =
К кг
Для газов удобно пользоваться молярной
теплоемкостью Сμ количество теплоты,
необходимое для нагревания 1 моля газа на 1
градус:
Дж
Сμ = с· μ
К моль
Молярные теплоемкости всех газов с одинаковым числом степеней
свободы i равны, а удельные – различны (т.к. разные молярные
массы μ)

5.

Теплоёмкость термодинамической системы
зависит от того, как изменяется состояние
системы при нагревании.
Наибольший
интерес
представляет
теплоемкость для случаев, когда нагревание
происходит при условии
V=Const (cV)
p=Const (cp) .

6.

V=Const (cV)
Если газ нагревать при постоянном объёме,
то всё подводимое тепло идёт на нагревание
газа, то есть изменение его внутренней энергии.
Работы над другими телами не совершается.
dQV = dU
Т.к. для 1 моля
(dА = 0)
i
U RT
2
dQ dU
CV
dT
dT
i
CV RT
2
Т.о. CV не зависит от температуры, а зависит только от числа
степеней свободы i равны, т.е. от числа атомов в молекуле газа.

7.

p=Const (cp)
Если нагревать газ при
постоянном давлении (СР) в сосуде с
поршнем, то подводимое тепло
затрачивается и на нагревание газа, и
на совершение работы.
Поэтому, для повышения Т на 1 К
понадобится больше тепла, чем в
случае V=Const
Следовательно, СР > СV

8.

dQ p dU pdV
Запишем I начало ТД для 1 моля газа
разделим на dT
Cp
dQ p
dT
dU
dT
CV
p(
dV
dT
) p CV R
Из основного уравнения МКТ имеем:
pVμ=RT
Vμ=RT/p
Т.о. работа, которую совершает 1 моль идеального газа при повышении
температуры на 1К равна газовой постоянной R.
отношение Cp/Cv есть постоянная для каждого газа величина
i
Cp 2 R R
2 i 2
1
i
CV
i
i
R
2

9.

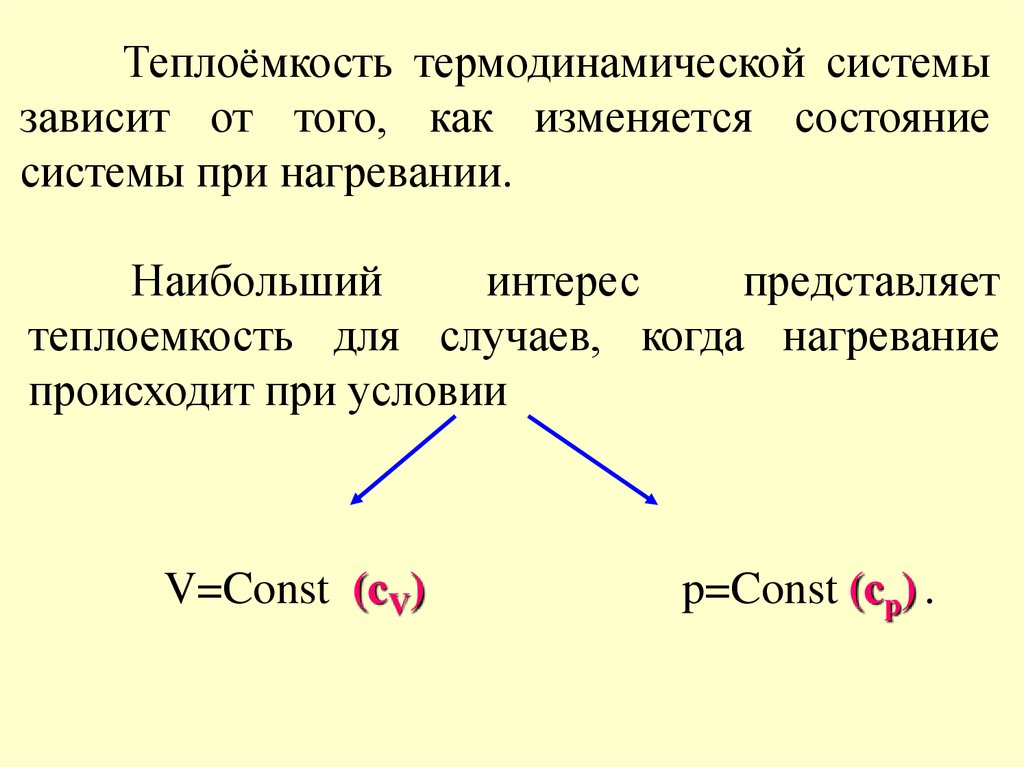
Число степеней свободы, проявляющееся в теплоемкости зависит от
температуры.
Рис. качественная зависимость молярной теплоемкости СV от
температуры для аргона (Ar) и водорода (H2)
Результаты МКТ верны для определенных температурных
интервалов, причем каждому интервалу соответствует свое число
степеней свободы.

10.

Применение первого начала
термодинамики к изопроцессам
Изопроцесс – процесс, проходящий при постоянном значении
одного из основных термодинамических параметров – P, V или Т.
1) изохорический процесс, при котором объем системы
остается постоянным (V = const).
2) изобарический процесс, при котором давление,
оказываемое со стороны системы на окружающие тела,
остается постоянным (р = const).
A p(V2 V1 )
3) изотермический процесс, при котором температура
системы остается постоянной (Т = const).
4) адиабатический процесс, при котором на протяжении
всего процесса теплообмен с окружающей средой
отсутствует (dQ = 0; Q = 0)
Q U A

11.

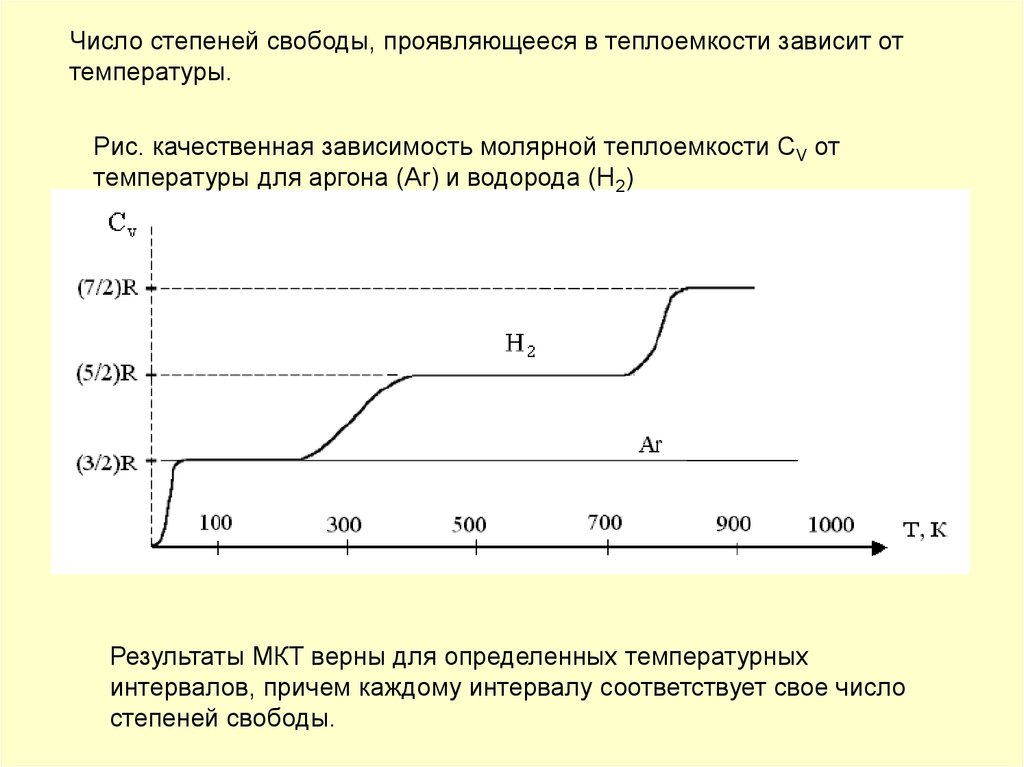
► Изотермический процесс – процесс,
происходящий в физической системе при постоянной
температуре (T = const).
В
идеальном газе при изотермическом
процессе произведение давления на объем постоянно
И зотер ма
– закон Бойля Мариотта:
PV const при T const . P
T3 > T2 > T1
T3
Найдем работу газа при
изотермическом процессе :
T2
T1
V
V2
A=
V1
V2
0
RT
V2
p1
pdV =
dV = RTln RTln
V
V1
p2
V1
V1
V2

12.

Используя формулу U = сVT ,
получаем
dU = сV dT = 0
Следовательно,
внутренняя
энергия
изотермическом процессе не меняется .
Поэтому
газа
при
Q A
Значит, при изотермическом процессе вся теплота,
сообщаемая газу, идет на совершение им работы над внешними
телами.
Поэтому
m
p1
Q = A = RTln
M
p2
Чтобы при расширении газа его температура не понижалась, к
газу необходимо подводить количество теплоты, равное его
работе над внешними телами.

13.

► Изохорический процесс – процесс,
происходящий в физической системе при постоянном
объеме (V = const).
P const при V const
T
- закон Шарля
При изохорическом процессе механическая
работа газом не совершается.
Q U

14.

Изохорический процесс: V = const
Из уравнения состояния идеального
газа для двух температур T1 и T2
следует
m
p1V = RT1
M
откуда
T2
p2 = p1
T1
В процессе 1
В процессе 1
Изохор а
.
.
.
P
m
p2V = RT2
M
2
0
2 происходит нагревание газа
3 происходит охлаждение газа
1
3
V

15.

Пусть начальное состояние газа отвечает состоянию при
нормальных условиях Т0 = 0°С = 273.15 °К, р0 = 1 атм, тогда для
произвольной температуры Т давление в изохорическом
процессе находится из уравнения
T
p = p0
T0
Давление газа пропорционально его температуре - Закон Шарля
Поскольку
dA = pdV = 0
, то при изохорическом
процессе газ не совершает работу над внешними телами.
При этом переданная газу теплота равна
dQ = dА + dU = dU
То есть при изохорическом процессе вся теплота,
передаваемая газу, идет на увеличение его внутренней энергии.
m
d'Q = dU = cV dT
M

16.

► Изобарический процесс – процесс,
происходящий в физической системе при
постоянном давлении (P = const).
V
T
const при P const
Q U А
- закон ГейЛюссака

17.

2) Изобарический процесс: p = const
В изобарическом процессе газ
совершает работу
Изобар а
P
V2
A=
pdV = p(V
2
.
-V1 )
1
V1
Работа равна площади под прямой
изобары. Из уравнения состояния
идеального газа получаем
m
pV1 = RT1
M
.
2
V
0
m
pV2 = RT2
M
m
A = p(V2 -V1 ) = R(T2 T1 )
M
V1
V2

18.

Перепишем последнее соотношение в виде
A
R=
ν(T2 - T1 )
Это равенство раскрывает физический смысл газовой
постоянной R - она равна работе 1 моля идеального газа,
совершаемой им при нагревании на 1° К в условиях
изобарного расширения.
Возьмем в качестве начального состояния - состояние
идеального газа при нормальных условиях (Т0, V0), тогда объем
газа V при произвольной температуре Т в изобарическом
процессе равен
T
V = V0
T0
Объем газа при постоянном давлении пропорционален его
температуре - закон Гей-Люссака.

19.

► Адиабатный процесс – процесс, происходящий в
физической системе без теплообмена с окружающей
средой (Q = 0).
PV const
уравнение Пуассона.
CP i 2
CV
i
γ – показатель адиабаты.
А U

20.

4) Адиабатический процесс : dQ = 0
При адиабатическом процессе теплообмен между газом и
окружающей средой отсутствует. Из первого начала
термодинамики получаем
dA = - dU
Поэтому в адиабатическом процессе работа газа над
внешними телами совершается за счет убыли его внутренней
энергии.
Используя
dU = сVdT ; dA = рdV
находим
рdV = - сV dT
С другой стороны, из уравнения состояния идеального газа
следует
d(рV) = pdV + Vdp = RdT

21.

Исключая
dT , получаем
рdV = - сV (pdV + vdp)/R
Откуда
dp
R dV
dV
= -( 1 + )
= -γ
p
cV V
V
Интегрируя, находим
p2
V2
dp
dV
=
-γ
p p V V
1
1
p2
V2
ln( ) = -γln( )
p1
V1

22.

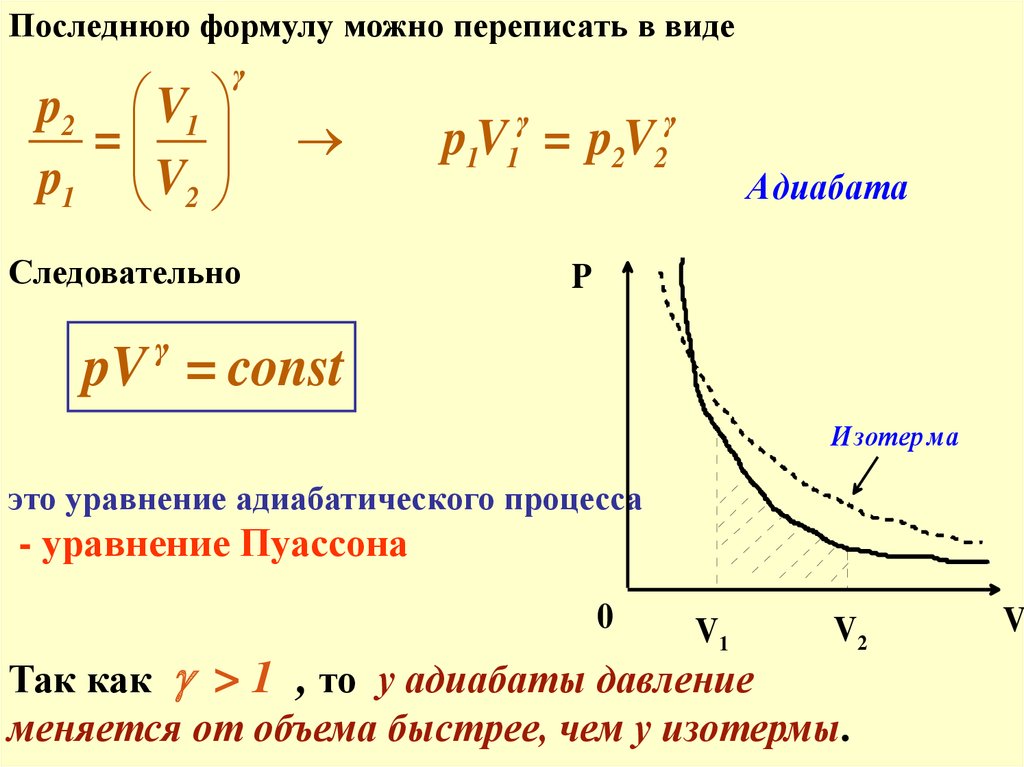
Последнюю формулу можно переписать в виде
p2 V1
=
p1 V2
γ
Следовательно
γ
1 1
γ
2 2
pV = pV
Адиабата
P
γ
pV = const
И зотер ма
это уравнение адиабатического процесса
- уравнение Пуассона
0
V1
V2
Так как > 1 , то у адиабаты давление
меняется от объема быстрее, чем у изотермы.
V

23.

Используя уравнение состояния
преобразуем уравнение Пуассона к виду
pV = νRT
Значит
или
TV
p
νRTV
(γ-1)
(1-γ)
(γ -1)
идеального
газа,
= const
= const
γ
T = const
При адиабатическом расширении идеальный газ
охлаждается, а при сжатии – нагревается.

24.

Политропический процесс
Политропический
процесс
–
процесс,
протекающий при постоянной теплоёмкости,
cm = const.
где cm – молярная теплоемкость.
pV const , n
n
c cp
c cV
где n - показатель политропы.
,

25.

Найдем уравнение политропы для идеального газа.
Из первого начала термодинамики следует
d'Q = dU + pdV = νcm dT
dU = νdU m = νcV dT
откуда получаем
ν(cm - cV )dT = pdV

26.

С другой стороны, из уравнения состояния идеального
газа
d(pV) = d(νRT) pdV +Vdp = νRdT
Поэтому можно записать
(cm - cV )(pdV + VdP) = pRdV
(cm - cV - R)pdV + (cm - cV )Vdp = 0
Поскольку
cP = cV + R то
dV
dp
(cm - cP )
+ (cm - cV ) = 0
V
p

27.

cm - c P
Обозначим n =
cm - cV
Интегрируем
Следовательно
, получим
dV dp
n
+ =0
V
p
V2
p1
nln = ln
V1
p2
p2V2n = p1V1n
n
pV = const
- уравнение политропы,
n - показатель политропы.

28.

Все изопроцессы являются частным случаем
политропического процесса:
pV const , n адиабата.
pV const , n 1 изотерма .
p const , n 0 изобара .
1
n
pV const , p V const ,
n V const изохора.
n

29.

Энтропия
Адиабатические процессы в термодинамических системах могут
быть равновесными и неравновесными. Для характеристики
равновесного адиабатического процесса можно ввести некоторую
физическую величину, которая оставалась бы постоянной в
течение всего процесса; ее назвали энтропией S.
Энтропия есть такая функция состояния системы, элементарное
изменение которой при равновесном переходе системы из одного
состояния в другое равно полученному или отданному количеству
теплоты, деленному на температуру, при которой произошел этот
процесс
для бесконечно малого изменения состояния системы
dQ cmdT
dS
T
T

30.

Изменение энтропии в изопроцессах
Если система совершает равновесный переход из
состояния 1 в состояние 2, то изменение энтропии:
dQ
dU A
S 2 S1
,
T
T
1
1
2
ΔS1 2
2
Найдем изменения энтропии в процессах идеального газа.
Так как
m
dU CV dT ,
μ
а
то
m RT
dA pdV
dV ,
V
2
2
m dT
mR
ΔS S 2 S1 CV
dV
μ
T 1 μV
1

31.

Или
T2 m
V2
m
ΔS Cv ln R ln
μ
T1 μ
V1
Изменение энтропии S1 2 идеального газа при
переходе его из состояния 1 в состояние 2 не
зависит от пути перехода 1 2.
изохорического
процесса:
изобарического
процесса:
T2
m
ΔS CV ln ,
μ
T1
V1 V2
T2 p1 = p2
m 2 dT2 m
ΔS C p
C p ln ,
μ T1
T1
μ
T1
T
изотермического
процесса:
V2
ΔS mR ln ,
V1
адиабатного
процесса:
dQ 0,
ΔS 0,
Т1 = Т2

32.

Следовательно, S = const, адиабатный процесс по другому
называют – изоэнтропийным процессом.
Во всех случаях, когда система получает извне теплоту, то Q —
положительно, следовательно, S2 > S1 и энтропия системы
увеличивается.
Если же система отдаст теплоту, то Q имеет отрицательный знак
и, следовательно, S2 < S1; энтропия системы уменьшается.
Энтропия системы пропорциональна массе (или числу частиц) этой
системы
Q=c m ΔT
Масса системы представляется в виде суммы масс ее составных
частей, поэтому энтропия всей системы будет равна сумме
энтропии ее составных частей, т. е. энтропия есть аддитивная
величина.

33.

Изопроцессы могут быть изображены графически в координатных
системах, по осям которых отложены параметры состояния.
давление p - объем V
температура Т– объем V
температура Т – давление p
p1V1 p2V2
const
T1
T2
V1
V2
T1 T2
p1 p2 const ( )
V1 V2
При адиабатическом расширении внешняя работа совершается только
за счет внутренней энергии газа, вследствие чего внутренняя энергия, а вместе
с ней и температура газа уменьшаются (Т2 < T1)
При изотермическом процессе Т2 = T1

34.

Удобство координатной системы р, V
В масштабе чертежа внешняя работа изображается
площадью, ограниченной кривой процесса 1—2 и
ординатами начального и конечного состояний

35.

Круговые (замкнутые) процессы
Совокупность термодинамических процессов, в
результате которых система возвращается в исходное
состояние, называется круговым процессом (циклом).
Прямой цикл – работа за
цикл
A pdV 0
Обратный цикл – работа
за цикл
A pdV 0

36.

Тепловая машина
Циклически действующее устройство, превращающее
теплоту в работу, называется тепловой машиной или
тепловым двигателем.
Q
Н агреватель
1
Рабочее
тело
Q
2
Х олодильни к
(Р Т )
А
Q1 – тепло, получаемое РТ от нагревателя,
Q2 – тепло, передаваемое РТ холодильнику,
А – полезная работа (работа, совершаемая РТ при
передаче тепла).

37.

2
2
1
1
Q
p
a
1
b
-Q
Q
1
2
1
-Q
2
0
2
V
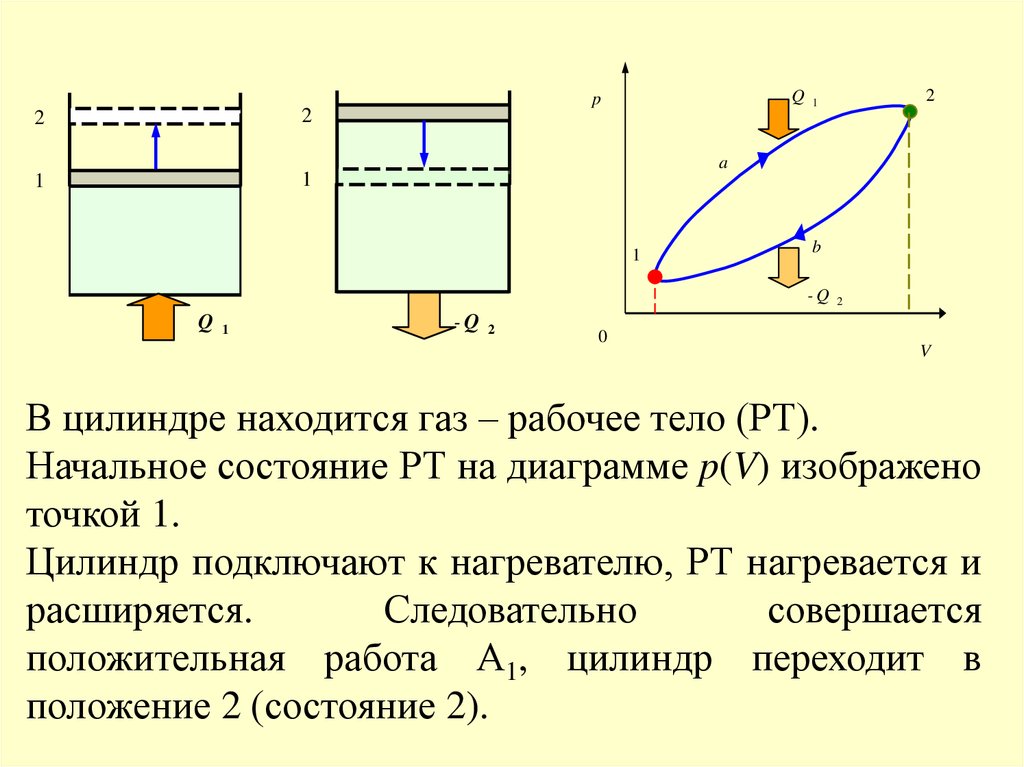
В цилиндре находится газ – рабочее тело (РТ).
Начальное состояние РТ на диаграмме p(V) изображено
точкой 1.
Цилиндр подключают к нагревателю, РТ нагревается и
расширяется.
Следовательно
совершается
положительная работа А1, цилиндр переходит в
положение 2 (состояние 2).

38.

Процесс 1–2: –
Q
p
2
1
Q1 U 2 U 1 A1
a
1
-Q
0
первое начало термодинамики.
b
2
V
Работа А1 равна площади под кривой 1a2.
Чтобы поршень цилиндра вернуть в исходное
состояние 1, необходимо сжать рабочее тело,
затратив при этом работу – А2.

39.

Q
p
2
1
a
1
b
-Q
0
Процесс 2–1:
2
V
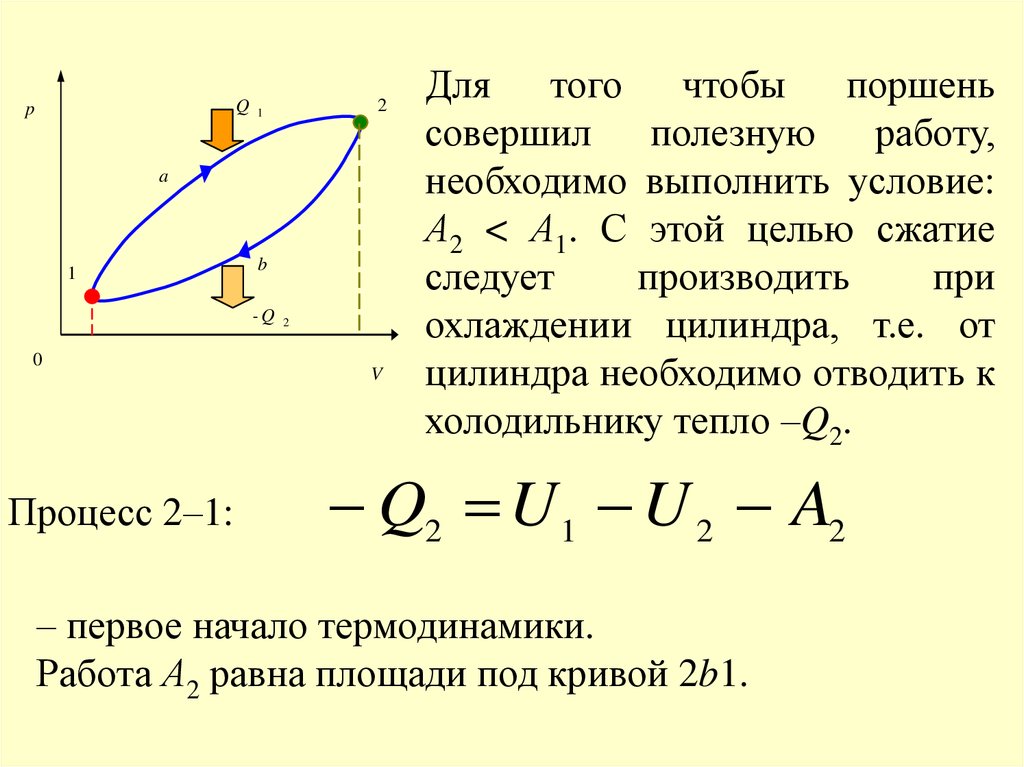
Для того чтобы поршень
совершил полезную работу,
необходимо выполнить условие:
А2 < А1. С этой целью сжатие
следует
производить
при
охлаждении цилиндра, т.е. от
цилиндра необходимо отводить к
холодильнику тепло –Q2.
Q2 U 1 U 2 A2
– первое начало термодинамики.
Работа А2 равна площади под кривой 2b1.

40.

Q
p
2
1
a
Сложим два уравнения и
получим:
Q1 Q2 A1 A2 Aпол езная .
b
1
-Q
0
2
V
Рабочее тело совершает круговой процесс 1a2b1 – цикл.
К.п.д.
Аполезная Q1 Q2
Q2
1 .
Q1
Q1
Q1

41.

Q
p
2
1
a
m
M
pV RT T pV
;
M
Rm
1
b
-Q
0
2
V
при V const , pнагревателя p холодильника Т н Т х .
Процесс возвращения рабочего тела в исходное
состояние происходит при более низкой температуре.
Следовательно, для работы тепловой машины
холодильник принципиально необходим.

42.

Цикл Карно
Никола Леонард Сади КАРНО – блестящий
французский офицер инженерных войск, в 1824 г.
опубликовал сочинение «Размышления о
движущей силе огня и о машинах способных
развить эту силу».
Ввел понятие кругового и обратимого
процессов, идеального цикла тепловых машин,
заложил тем самым основы их теории. Пришел к
понятию механического эквивалента теплоты.

43.

Карно вывел теорему, носящую теперь его
имя:
из всех периодически действующих
тепловых машин, имеющих одинаковые
температуры нагревателей и холодильников,
наибольшим КПД обладают обратимые
машины. Причем КПД обратимых машин,
работающих при одинаковых температурах
нагревателей и холодильников, равны друг другу
и не зависят от конструкции машины. При
этом КПД меньше единицы.

44.

45.

Процесс А-В – изотермическое расширение
V1
A1 RT1ln Q1 ,
V0
Процесс В-С – адиабатическое расширение.
γ 1
T1 V2
,
T2 V1
– коэффициент Пуассона.
p1V1 (T1 T2 ) R T1 T2
A2
1
( 1)T1

46.

Процесс С-D – изотермическое сжатие
V3
A3 RT2ln Q2
V2
Процесс D-A – адиабатическое сжатие.
V3
V0
γ 1
T1
T2
R
A4
(T1 T2 )
1

47.

V1 R(T1 T2 )
A RT1 ln
V0
1
V3 R(T1 T2 )
RT2 ln
V2
1
Q2
T2
A Q1 Q2
η
1 1
Q1
Q1
Q1
T1

48.

Если Т2 = 0, то η = 1, что невозможно, т.к.
абсолютный нуль температуры не существует.
Если Т1 = ∞, то η = 1, что невозможно, т.к.
бесконечная температура не достижима.
КПД цикла Карно η < 1 и зависит от
разности температур между нагревателем и
холодильником (и не зависит от конструкции
машины и рода рабочего тела).

49.

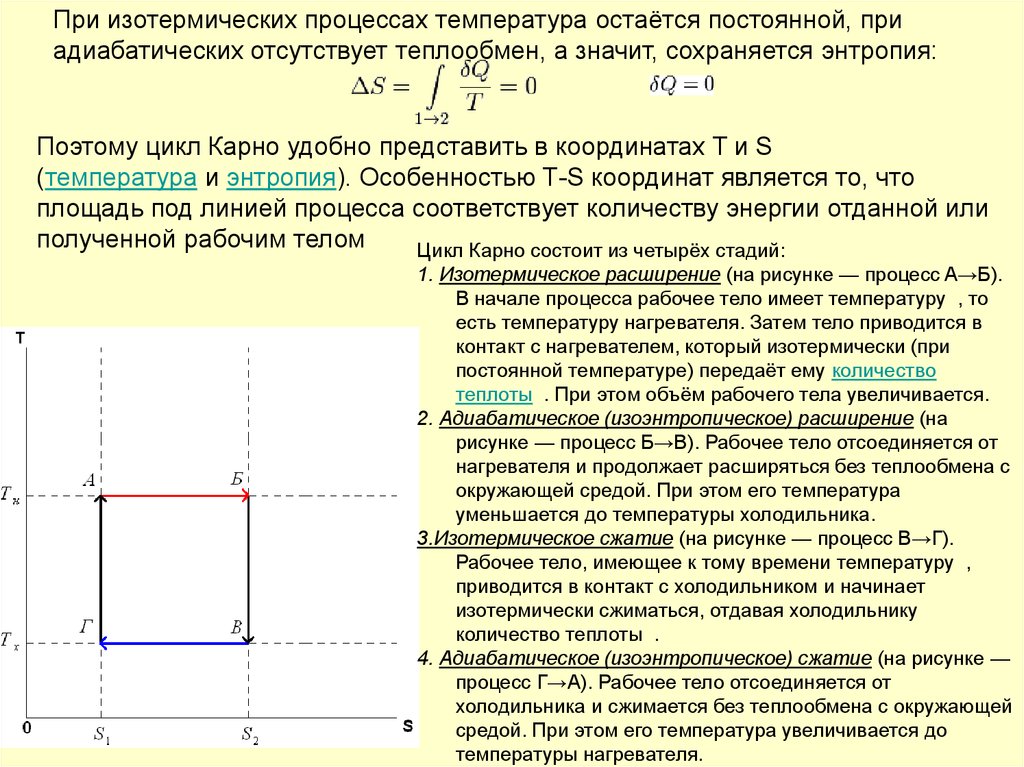
При изотермических процессах температура остаётся постоянной, при
адиабатических отсутствует теплообмен, а значит, сохраняется энтропия:
Поэтому цикл Карно удобно представить в координатах T и S
(температура и энтропия). Особенностью Т-S координат является то, что
площадь под линией процесса соответствует количеству энергии отданной или
полученной рабочим телом
Цикл Карно состоит из четырёх стадий:
1. Изотермическое расширение (на рисунке — процесс A→Б).
В начале процесса рабочее тело имеет температуру , то
есть температуру нагревателя. Затем тело приводится в
контакт с нагревателем, который изотермически (при
постоянной температуре) передаёт ему количество
теплоты . При этом объём рабочего тела увеличивается.
2. Адиабатическое (изоэнтропическое) расширение (на
рисунке — процесс Б→В). Рабочее тело отсоединяется от
нагревателя и продолжает расширяться без теплообмена с
окружающей средой. При этом его температура
уменьшается до температуры холодильника.
3.Изотермическое сжатие (на рисунке — процесс В→Г).
Рабочее тело, имеющее к тому времени температуру ,
приводится в контакт с холодильником и начинает
изотермически сжиматься, отдавая холодильнику
количество теплоты .
4. Адиабатическое (изоэнтропическое) сжатие (на рисунке —
процесс Г→А). Рабочее тело отсоединяется от
холодильника и сжимается без теплообмена с окружающей
средой. При этом его температура увеличивается до
температуры нагревателя.

50.

Теоремы Карно.
1. К.п.д. η обратимой идеальной тепловой
машины Карно не зависит от рабочего
вещества.
2. К.п.д. необратимой машины Карно не может
быть больше к.п.д. обратимой машины Карно.