Похожие презентации:
Дискретная математика. Отношения на множествах. Бинарные отношения и их свойства
1. Дискретная математика
3 Отношения на множествах.Бинарные отношения
и их свойства
2.
Отношения на множествахС отношениями между элементами
множеств имеем дело повсеместно. Это отношения равенства на произвольных
числовых множествах, отношения «больше» и
«меньше» между числами, отношения подобия
фигур, на плоскости и т. д.
Так функцию можно рассматривать как
частный случай отношений.
При этом легче понять обратимость
функций и многое другое их касаемо.
3.
Декартово произведение n одинаковых сомножителейА А … А обозначается символом AN и называется n-й
степенью множества А. При этом А1 = А. Примером декартова
произведения является R R = R2 – множество точек на
плоскости. Здесь элементы х R и у R служат
координатами некоторой точки на плоскости. Другим
примером является множество R3 точек в трехмерном
евклидовом пространстве. Обобщением этих понятий
является n -мерное пространство.
Любое подмножество R А1 А2 … Аn декартова
произведения п множеств называется n-арным
отношением. При n = 1, 2, 3 имеем унарное, бинарное,
тернарное отношения соответственно. Унарное
отношение на множестве А представляет собой
подмножество множества А.
4.
1. Многоместные отношенияПусть X и Y два не пустых множества
5.
6.
7.
Еще пишут y = f(x), x X, как в анализе8.
9.
Многоместные отношения.10.
11.
2 Бинарные отношенияБинарным отношением, или соответствием между элементами
множеств А и В, называется любое подмножество R А В
декартова произведения этих множеств. Тот факт, что некоторые
a A и b В находятся в отношении R, иногда выражают как a R b.
В качестве примера бинарного отношения рассмотрим отношение R
между элементами множеств А = {1, 2, 3} и B = {1, 2, 3, 4, 5, 6},
которое можно выразить словами так: элемент х A есть делитель
элемента у В. Тогда имеем
R = {(1, 1), (1, 2), (1, 3), (1, 4), (1, 5),
(1, 6), (2, 2), (2, 4), (2, 6), (3, 3), (3, 6)}.
12.
Бинарное отношение удобно представлять в виде двоичной(булевой) матрицы. При этом элементы множеств А и В должны
быть пронумерованы, и если i-й элемент множества А
соответствует j-му элементу множества В, то элемент матрицы,
расположенный на пересечении i-й строки и j-го столбца, имеет
значение 1, в противном случае он имеет значение 0.
Например, рассмотренное выше отношение R будет представлено
следующей матрицей:
Проекция элемента (a, b) множества А В на множество А
есть элемент а. Аналогично элемент b является проекцией
элемента (a, b) множества А В на множество В.
13.
Проекцией множества Е А В на А называетсямножество всех тех элементов из А, которые являются
проекциями элементов из Е на множество А. Для множеств
А и В, рассмотренных выше, проекцией элемента (2, 4) на
множество А является элемент 2, а проекцией множества
{(1, 2), (2, 2), (2, 4)} – множество {1, 2}.
14.
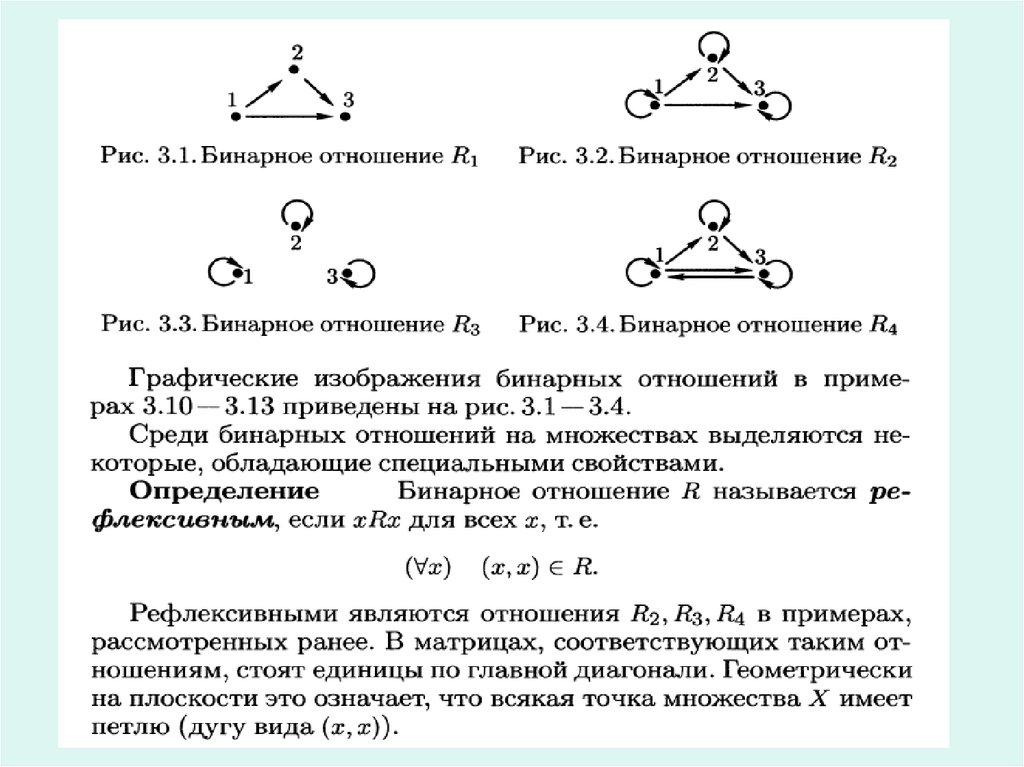
Бинарные отношения на множестве15.
16.
17.
18.
19.
20.
21.
22.
23.
24.
25.
26.
27.
28.
29.
30.
31.
32.
33.
34.
Соответствие между равными множествамиА = В называется отношением на данном
множестве (А).
Отношения в некоторых числовых
множествах могут выражаться терминами:
«быть равным», «быть больше», «быть не
меньше», «быть делителем» и т.д.
Отношения во множестве линий на
плоскости могут выражаться терминами: «быть
параллельными», «пересекаться», «касаться»
и т.д.
35.
Подмножество R M n называется n-местнымотношением R на непустом множестве М. При
n=2 отношение R называется бинарным.
То есть бинарным отношением между
элементами множеств А и В называют любое
подмножество R множества АхВ и записывают
R АхВ.
Для отношения R обратным является
отношение R-1 BxA.
36. Композиция отношений
37.
Бинарные отношения принято записывать ввиде aRb, где а, b М. Запись читается как «а
и b находятся в отношении R».
Например, а||b (параллельные прямые), а b
(действительные числа), а = logc b и т.д.
Рассмотрим примеры бинарных отношений.
Бинарное отношение R: х у
показано на рис. Заштриховано
множество точек, для координат
которых это отношение
выполняется (истинно).
38.
Графики прямых и обратных бинарныхотношений, определенных на множестве
действительных чисел, симметричны
относительно биссектрисы I и III квадрантов.
Это свойство обратных бинарных отношений
используют при построении графиков
обратных функций, например: у = log2x и у=2х
Пример 1.
у = х2 и
у = x,
где х О
(рис. a);
39.
Пример 2.у = sin x и у = arcsin x, где 0 х /2 (рис. б).
40. Свойства бинарных отношений:
1) рефлексивность:a M a, a R
Например: «быть не больше»; «быть
делителем» на множестве N; «быть
коллинеарным» на множестве векторов;
41. Свойства бинарных отношений:
2) антирефлексивность:a M a, a R
Это отношение имеет место, когда оно не
обладает свойством 1 для любых а,
например: «быть больше», «быть
младше», «быть перпендикулярной» на
множестве прямых и др.
42. Свойства бинарных отношений:
3) симметричность:a, b M a, b R b, a R
Отношение R на множестве М называется
симметричным, если для любых a, b M
одновременно справедливо aRb и bRa
(т.е.R=R-1).
Например:
Симметрична параллельность прямых, так как
если а || b, то b || а. Симметрично отношение
«быть равным» на любом множестве или «быть
взаимно-простым» на N.
43. Свойства бинарных отношений:
4) антисимметричность:a, b M a, b R, b, a R a b
Если для несовпадающих элементов а b
верно отношение aRb, то ложно bRa.
Антисимметричными являются отношения
«быть больше», «не меньше» на множестве R,
«быть делителем» на множестве N и др.
44. Свойства бинарных отношений:
5) транзитивность:a, b, c M a, b R, b, c R a, c R
Если aRb и bRc, то aRс для любых a, b, c M.
Транзитивны отношения «быть больше», «быть
параллельным», «быть равным» и др.
45. Свойства бинарных отношений:
6) антитранзитивность:a, b, c M a, b R, b, c R a, c R
Имеет место, когда отношение не обладает
свойством 5. Например, «быть
перпендикулярным» на множестве прямых
плоскости ( а b, b с, но неверно a с).
46. Свойства бинарных отношений:
7) асимметричность:a, b M a, b R b, a R
Ни для одной пары а и b не выполняется
одновременно aRb и bRa.
Например: «быть больше»; «быть меньше»;
«быть отцом».
47. Свойства бинарных отношений:
8) связность:a, b M a, b R или b, a R
Для любых а и b, если а b, то aRb или bRa.
Например: «быть больше», «быть меньше» на
множестве N, R; «быть больше или равным»,
«быть меньше или равным» на множестве
обыкновенных дробей.
Каждое конкретное отношение может обладать
или не обладать указанным свойством.
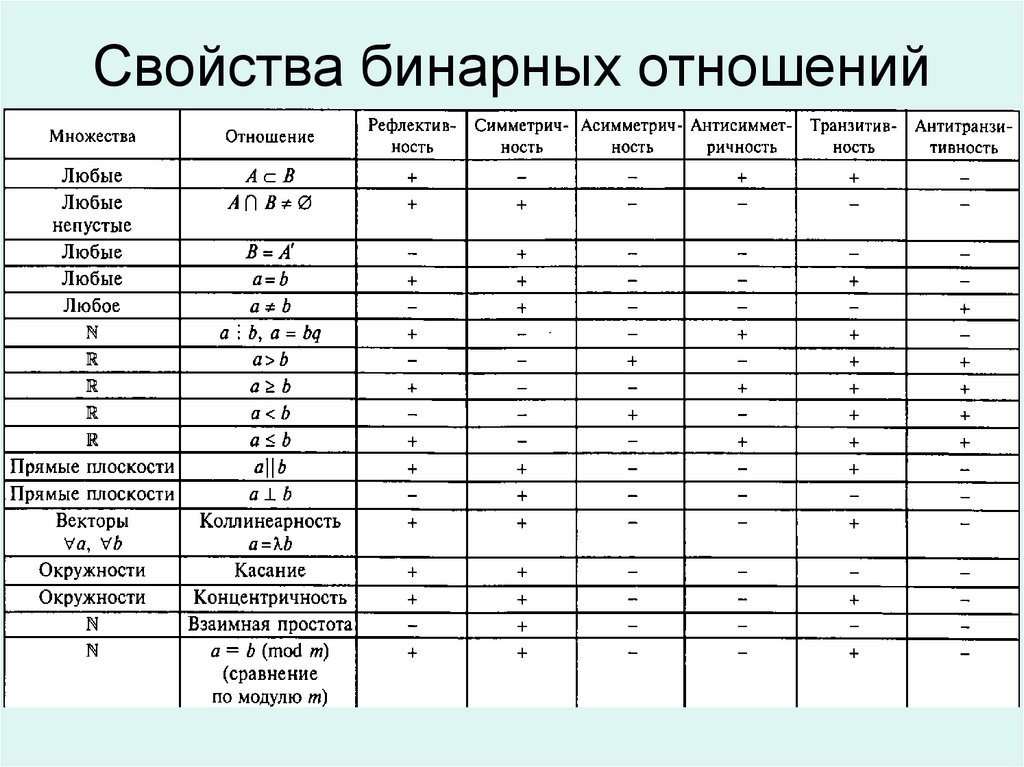
48. Свойства бинарных отношений
49. Основные виды бинарных отношений.
Бинарное отношение R называетсяотношением эквивалентности, если оно
одновременно обладает тремя свойствами:
рефлективностью, симметричностью и
транзитивностью, т.е. если для любых х, у, z
выполняется:
• xRx (рефлективность);
• если xRy, то уRх (симметричность);
• если xRy, a yRz, то xRz (транзитивность).
50.
Отношение эквивалентностирефлексивность
симметричность
транзитивность
Примеры отношений эквивалентности:
Отношение «быть равным на множестве
чисел», быть подобным на множестве
геометрических фигур.
Обозначение эквивалентных отношений:
a Q b или а ~ b, что означает «а эквивалентно b
в отношении Q»
51.
Непересекающиесяподмножества,
на
которые разбивается множество М отношением
эквивалентности,
называются
классами
эквивалентности.
На множестве обыкновенных дробей все
классы
эквивалентности
по
отношению
равенства состоят из дробей, равных по своей
величине.
На множестве треугольников все классы
эквивалентности по отношению подобия
состоят из треугольников, подобных между
собой.
52.
Отношение толерантностирефлексивность
симметричность
Отношение эквивалентности – частный
случай отношения толерантности.
Отношения
«быть
другом»,
«быть
знакомым»,
- отношения толерантности, так
как они рефлексивны, симметричны, но не
транзитивны.
Отношение «иметь непустое пересечение»
для множеств – отношение толерантности.
53.
Отношение порядкаантисимметричность
транзитивность
Множество М, которое обладает отношением
порядка, называется упорядоченным.
+ рефлексивность
Отношение
нестрогого порядка
≤
+ антирефлексивность
Отношение
строгого порядка <
54.
Отношение называется отношением полногопорядка, если сравнимы все элементы
множества, на котором задано это отношение.
Пример. Отношения «больше» и «меньше»
на множестве действительных чисел.
Отношение
называется
отношением
частичного порядка, если сравнимы не все
элементы множества, на котором задано это
отношение.
Пример. Отношение «быть подмножеством»
на множестве В(U) (булеан).




















































 Математика
Математика








