Статика межфазного распределения микрокомпонентов-радионуклидов

1. НЕДОБУХ ТАТЬЯНА АЛЕКСЕЕВНА Доцент кафедры радиохимии и прикладной экологии ФтИ

Основы ядерной физики,
радиохимии и дозиметрии
Лекция 7
СТАТИКА
МЕЖФАЗНОГО РАСПРЕДЕЛЕНИЯ
МИКРОКОМПОНЕНТОВ-РАДИОНУКЛИДОВ
НЕДОБУХ ТАТЬЯНА АЛЕКСЕЕВНА
Доцент кафедры радиохимии и прикладной экологии ФтИ

2. Содержание лекции

Статика
межфазного
распределения
при
катионообменном механизме извлечения.
Вывод гиперболической изотермы на основании закона
действующих масс (изотерма Ленгмюра). Линейная
изотерма (изотерма Генри).
Влияние
[m]
на
равновесное
распределение
микрокомпонента между фазами для случая коллектора
в H+ - форме. Лабильные и инертные системы.
Влияние концентрации фонового электролита.
Влияние концентрации лиганда.
Влияние величины рН водного раствора: для случая
поглотителя в форме катиона солевого фона; для
случая поглотинетя в Н+ форме.
Возможности разделения радионуклидов.

3. Ионный обмен с участием неорганических сорбентов

Реакции катионного обмена
z R Э M z Rz M zЭ ,
где Мz+ - катион сорбата-микрокомпонента с зарядом z+; R- - полианион
матрицы сорбента (гидроксида, оксисульфида, оксифосфата,
ферроцианида и т.п.); Э+ ≡ H+, K+, Na+, NH4+ и т.п. - ионообменивающийся катион, входящий в структуру сорбента (в общем
случае может иметь любой заряд Эz+).
Реакции анионного обмена
m
mR A L
Rm L mA ,
где Lm- - анионы раствора, в том числе анионные формы сорбата
микрокомпонента, R+ - поликатион матрицы сорбента; А- ≡ OH-, HS-,
H2PO4-, HSO4- и т.п. - обменивающиеся анионы, входящие в
структуру сорбента (в общем случае - Ay-).

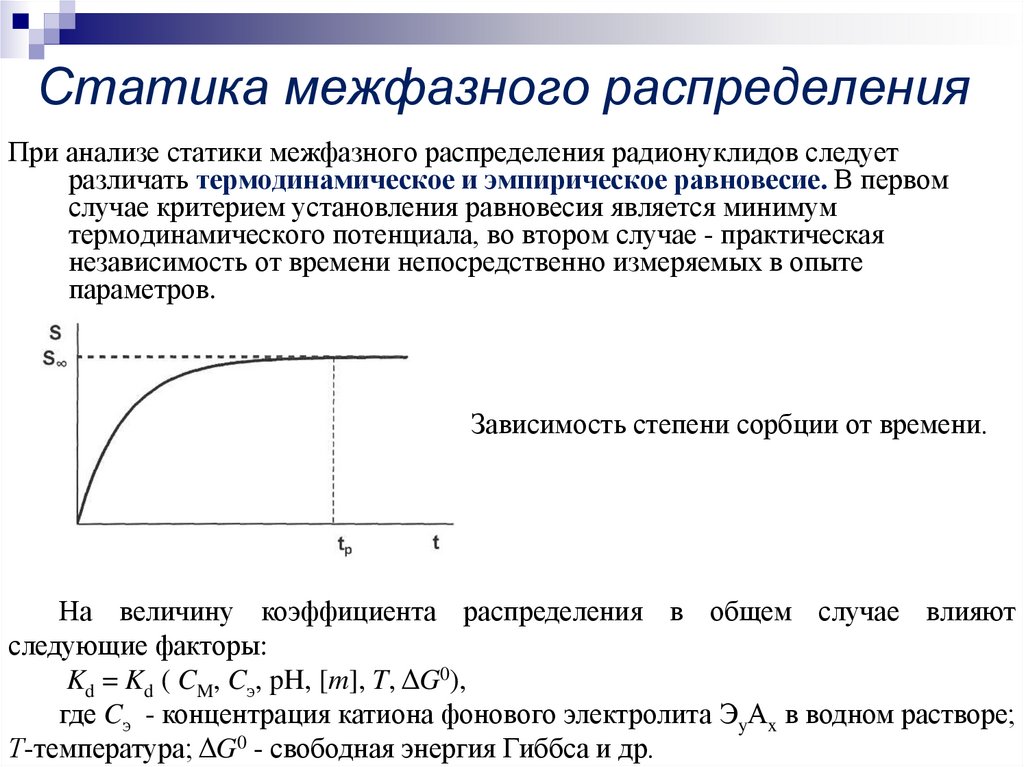
4. Статика межфазного распределения

При анализе статики межфазного распределения радионуклидов следует
различать термодинамическое и эмпирическое равновесие. В первом
случае критерием установления равновесия является минимум
термодинамического потенциала, во втором случае - практическая
независимость от времени непосредственно измеряемых в опыте
параметров.
Зависимость степени сорбции от времени.
На величину коэффициента распределения в общем случае влияют
следующие факторы:
Kd = Kd ( CM, Cэ, pH, [m], T, ΔG0),
где Cэ - концентрация катиона фонового электролита ЭyАx в водном растворе;
Т-температура; ΔG0 - свободная энергия Гиббса и др.

5. Влияние концентрации сорбата

Предположим, что процесс межфазного распределения протекает
по реакции катионного обмена:
z R Э M z Rz M zЭ
В соответствии с законом действующих масс термодинамическую
константу равновесия реакции можно записать в виде:
KT
aM aЭz
aM a
z
Э
f M [M ] f Эz [Э]z
f M [M ] f Эz [Э]z
где a = fC - термодинамическая активность, здесь f - коэффициент
активности.
Выразим коэффициент распределения и предположим, что в
качестве противоиона выступает Н+:
[M ]
f M f Эz [Э]z
f M aH
Kd
KT
KT
z
z
[M ]
f M f Э [ Э]
f M a H

6. Изотерма Генри

Условия выполнения изотермы Генри:
Сорбцию ведут из разбавленных растворов, следовательно,
fM = const.
Взаимодействия в твердой фазе не происходит, следовательно
f const.
M
рН = const.
Изотерма Генри:
C Kd C p

7. Изотерма Ленгмюра

Теория Ленгмюра является фундаментальным вкладом в
учение о сорбции. Наиболее сильное отклонение от
закона Генри связаны с ограниченностью доступной
поверхности сорбента. Это положение уточняется
следующими допущениями:
■
■
■
Сорбция локализована на отдельных сорбционных центрах,
каждый из которых взаимодействует только с одной молекулой
сорбата.
Сорбционные центры энергетически эквивалентны.
Сорбированные молекулы не взаимодействуют друг с другом.
Проанализируем термодинамическую константу равновесия
реакции катионного обмена

8.

Ионообменные центры поглотителя могут быть заняты
ионами сорбата, либо ионами конкурента:
Г = CM + C Э
поглотителя.
KT
-
полная
aM a H
f M [ M ] aH
aM a H
f M [ M ] f H ( [ M ])
CM
K f f
T M H
CM ( [ M ])
f M aH
a
ионообменная
либо
емкость
при обозначении СM [ M ], CM [ M ]
KT f M f H
.
f M aH
Изотерма Лэнгмюра
a CM
CM
1 a CM
a C P
или в других обозначени ях СT
1 a CP
a = const – параметр сорбционного сродства.

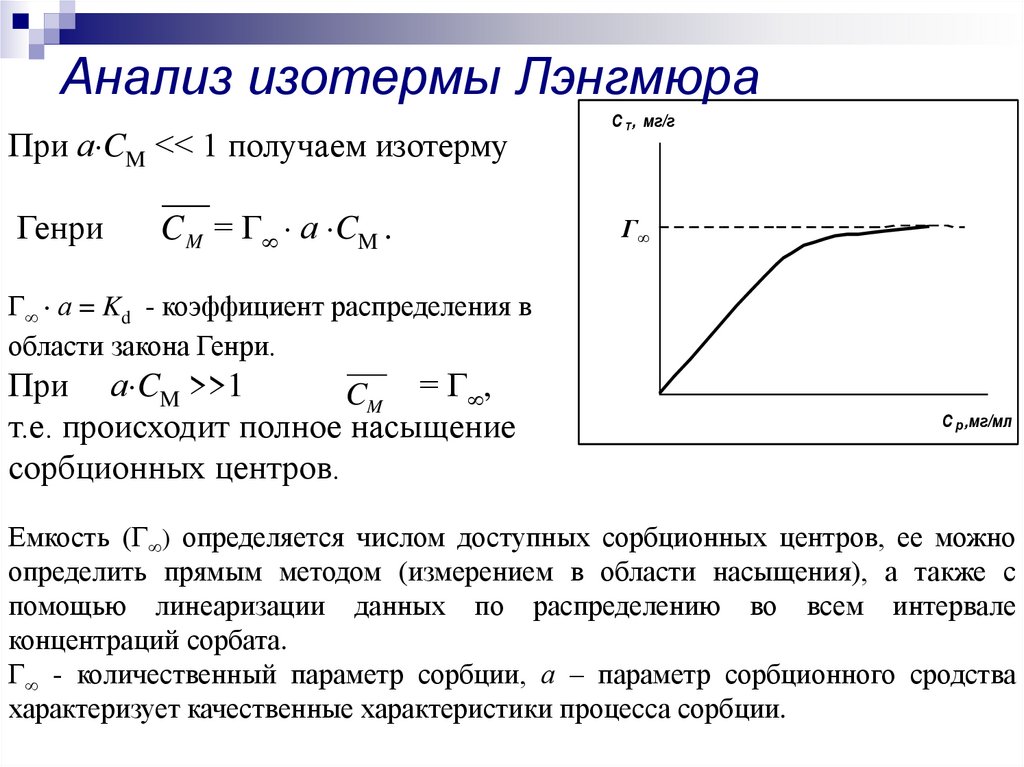
9. Анализ изотермы Лэнгмюра

При а CM << 1 получаем изотерму
Генри
C M = Г а CM .
С Т , мг/г
Г∞
Г а = Kd - коэффициент распределения в
области закона Генри.
При а CM >>1
CM = Г ,
т.е. происходит полное насыщение
сорбционных центров.
С р ,мг/мл
Емкость (Г ) определяется числом доступных сорбционных центров, ее можно
определить прямым методом (измерением в области насыщения), а также с
помощью линеаризации данных по распределению во всем интервале
концентраций сорбата.
Г - количественный параметр сорбции, а – параметр сорбционного сродства
характеризует качественные характеристики процесса сорбции.

10.

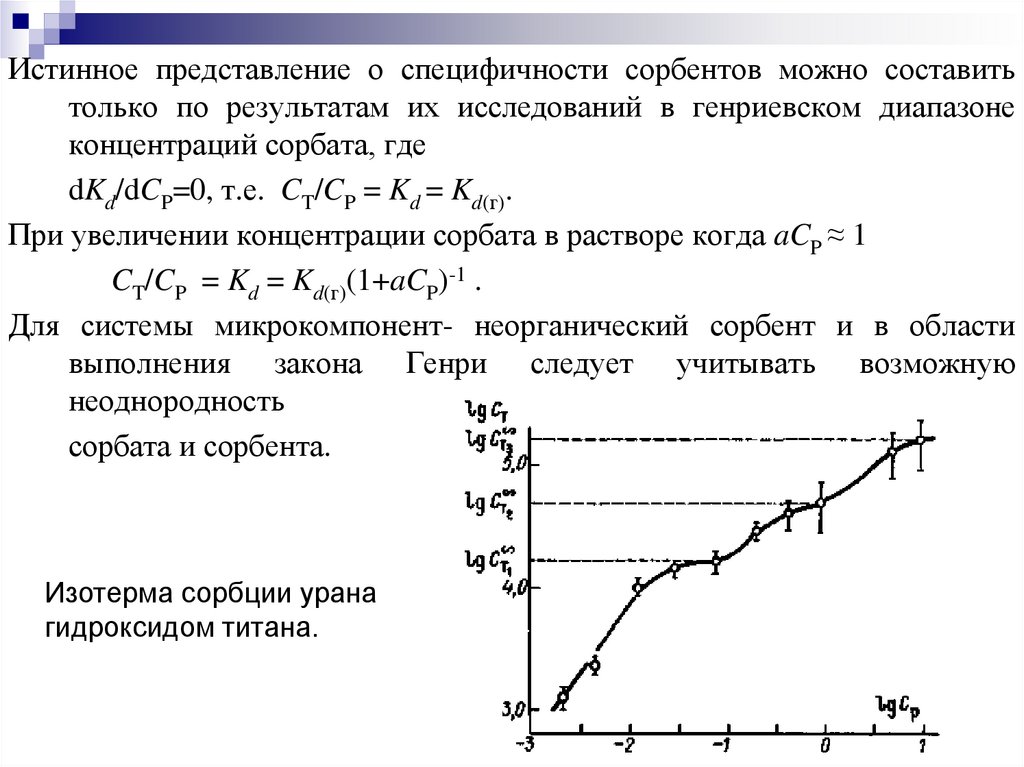
Истинное представление о специфичности сорбентов можно составить
только по результатам их исследований в генриевском диапазоне
концентраций сорбата, где
dKd/dCP=0, т.е. CT/CP = Kd = Kd(г).
При увеличении концентрации сорбата в растворе когда aCP ≈ 1
CT/CP = Kd = Kd(г)(1+aCP)-1 .
Для системы микрокомпонент- неорганический сорбент и в области
выполнения закона Генри следует учитывать возможную
неоднородность
сорбата и сорбента.
Изотерма сорбции урана
гидроксидом титана.

11. Влияние удельного содержания сорбента в системе

Сорбат-микрокомпонент представлен
единственной формой. Сорбционное поведение описывается законом Генри:
e = Kd[m] .
Kd не зависит от удельной массы сорбента.
Сорбат - микрокомпонент представлен
разносорбирующимися сортами, между
которыми имеется подвижное равновесие,
αi = const ≠ f[m] .
M z+ ML(z-1)+ ML(z-2)+ MLz0 … MLn (z-n)Kd не зависит от удельной массы сорбента,
характеризует сорбирующуюся форму.
ki ≠ f[m], т.е. dlgki /dlg[m] =0 d lgei / d lg[m] = 1
Сорбат называется сложным лабильным сорбатом.
Моносортовой или сложный
лабильный сорбат

12. Сложный инертный сорбат

Сорбат - микрокомпонент представлен несколькими разносорбирующимися
формами, между которыми отсутствует подвижное равновесие,
αi = f[m ]≠ const..
Такой сорбат называется сложным инертным сорбатом.
M z+ ← ML1 (z-1)+ ← ML2 (z-2)+ ← MLz0 ← ← MLn (z-n)Изотерма имеет сложный профиль, Kd является брутто-коэффициентом
распределения
Имеются несорбирующие сорта.
Сорбирующиеся формы отличаются значениями
частных генриевских постоянных.

13. Влияние концентрации фонового электролита (Cэ = var)

Фоновый электролит называют нейтральным, если его хорошо
диссоциирующая, растворимая соль ЭА при введении в раствор не
изменяет значение величины рН, а анион А- не вступает в реакции
комплексообразования с ионами сорбата.
z R Э M z Rz M zЭ
Тогда, если сорбат в растворе представлен единственной формой
состояния M(OH)iz-i, то для коэффициента распределения i-формы ki
можно записать
KT
aM aЭz i
aM a
z i
Э
f M [ M (OH )iz i ] aЭz i
f M [ M (OH )iz i ] aЭz i
KT f M aЭz i
где ki '
fM
KT f M aЭz i
i z
ki
k
'
a
i
Э ,
z i
f M aЭ
ki’=const

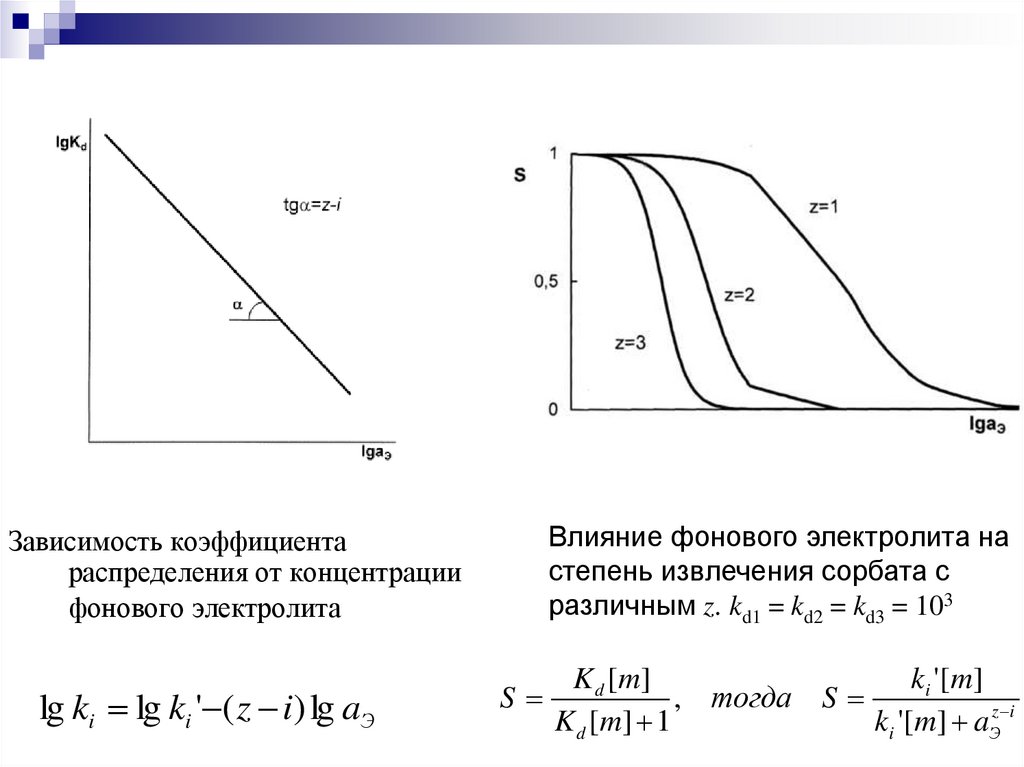
14.

Зависимость коэффициента
распределения от концентрации
фонового электролита
lg ki lg ki ' ( z i) lg aЭ
Влияние фонового электролита на
степень извлечения сорбата с
различным z. kd1 = kd2 = kd3 = 103
K d [ m]
k i ' [ m]
S
, тогда S
K d [ m] 1
ki '[m] aЭz i

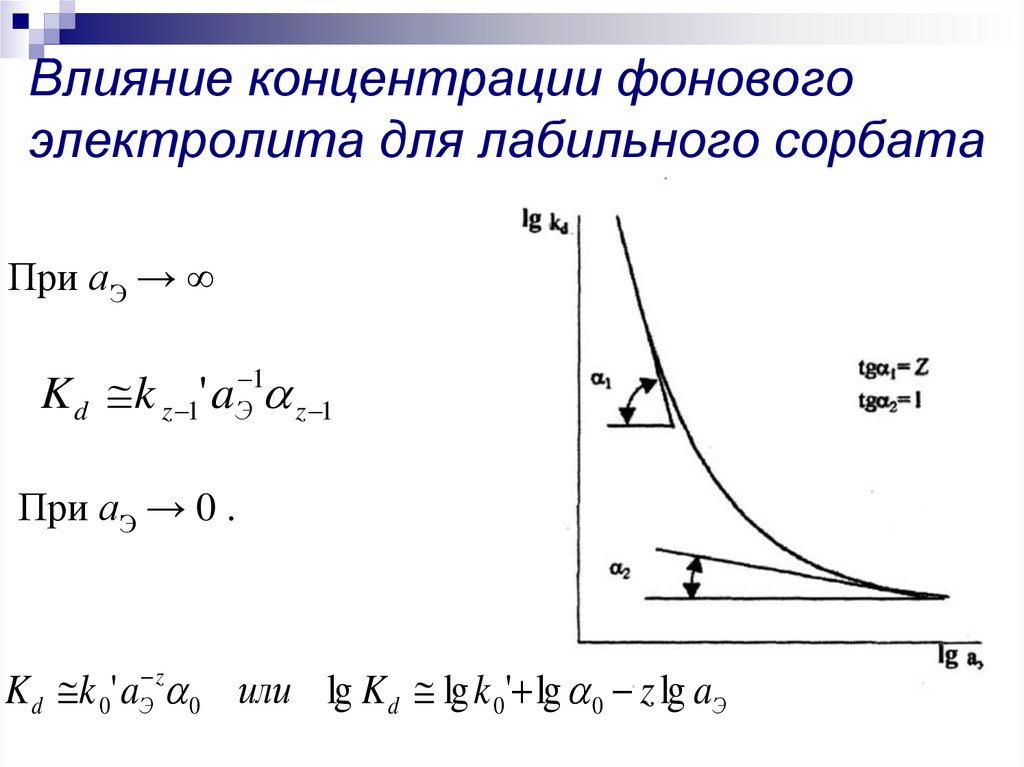
15. Влияние концентрации фонового электролита для лабильного сорбата

При аЭ → ∞
K d k z 1' aЭ 1 z 1
При аЭ → 0 .
K d k 0' aЭ z 0 или lg K d lg k 0' lg 0 z lg aЭ

16. Влияние концентрации фонового электролита для инертного сорбата

В случае инертного сорбата,
представленного в растворе только
сорбирующимися формами состояния:
z 1
K d ki' i
i 0
Если инертный сорбат представлен в том
числе и несорбирующимися формами,
для которых ki≥z=0, то
Влияние концентрации фонового
при аЭ → 0 предельное значение
Кd = Кd (max)
электролита для инертного
сорбата, представленного
сорбирующимися и
несорбирующимися формами

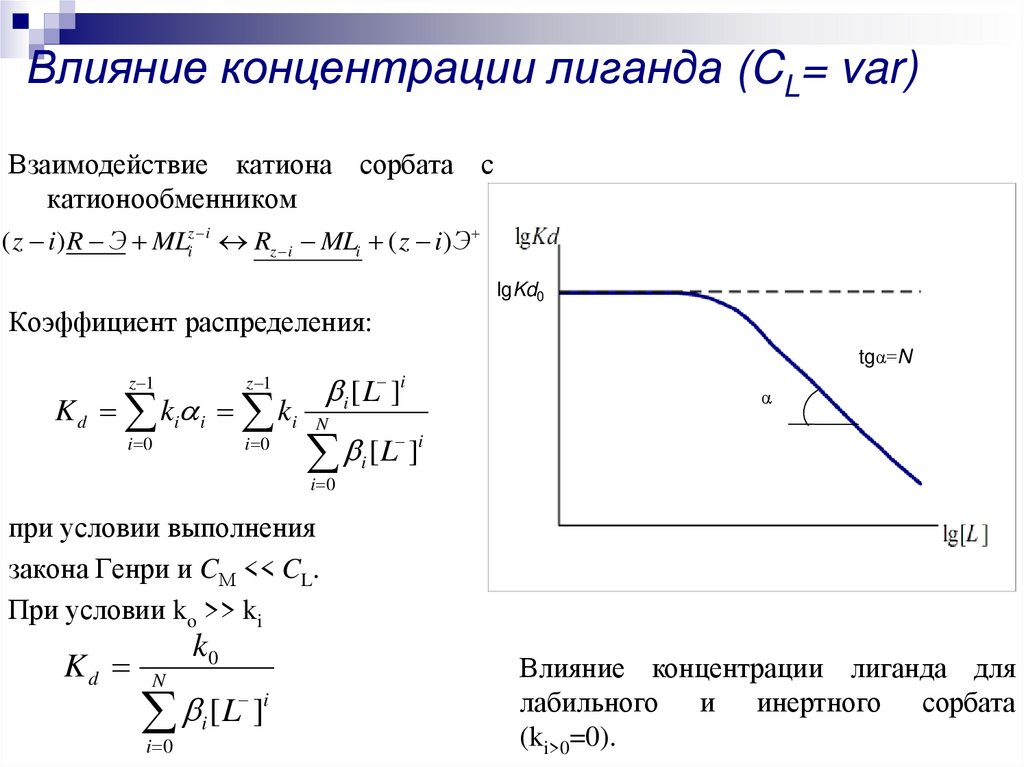
17. Влияние концентрации лиганда (CL= var)

Взаимодействие катиона сорбата с
катионообменником
( z i) R Э MLiz i Rz i MLi ( z i)Э
lgKd0
Коэффициент распределения:
tgα=N
z 1
i [ L ]i
z 1
K d ki i ki
i 0
i 0
α
N
i
[
L
i ]
i 0
при условии выполнения
закона Генри и CМ << CL.
При условии ko >> ki
Kd
k0
N
i
[
L
i ]
i 0
Влияние концентрации лиганда для
лабильного и инертного сорбата
(ki>0=0).

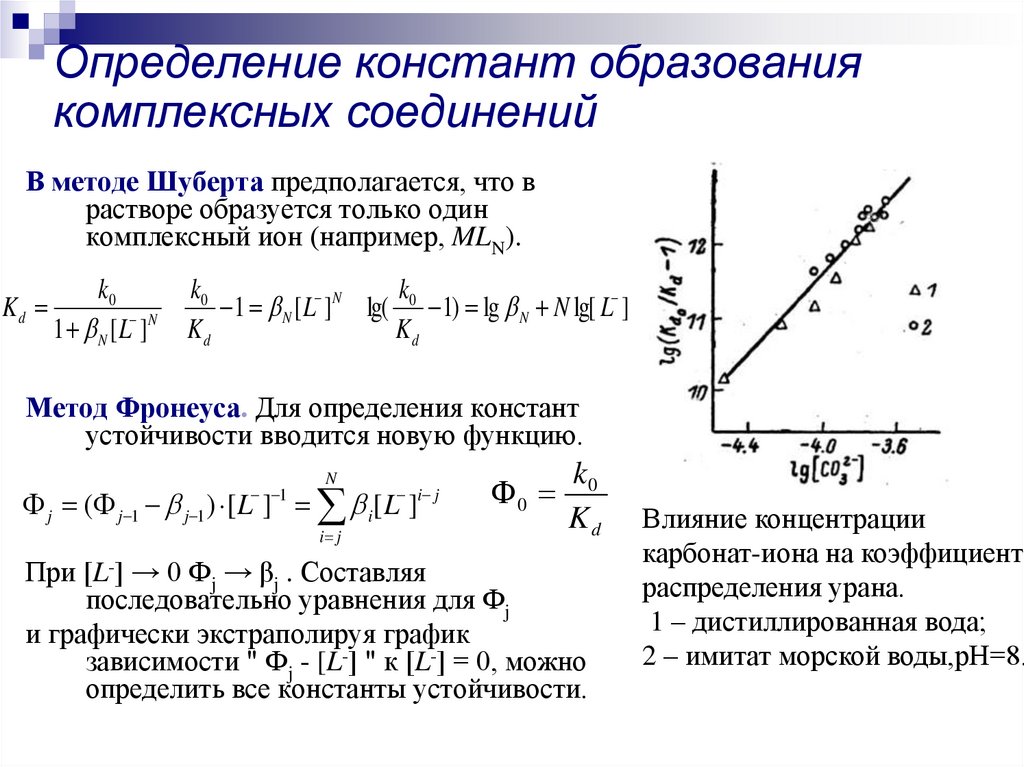
18. Определение констант образования комплексных соединений

В методе Шуберта предполагается, что в
растворе образуется только один
комплексный ион (например, MLN).
Kd
k0
1 N [ L ]N
k0
k
1 N [ L ]N lg( 0 1) lg N N lg[ L ]
Kd
Kd
Метод Фронеуса. Для определения констант
устойчивости вводится новую функцию.
N
j ( j 1 j 1 ) [ L ] 1 i[ L ]i j
i j
k0
0
Kd
При [L-] → 0 Фj → βj . Составляя
последовательно уравнения для Фj
и графически экстраполируя график
зависимости " Фj - [L-] " к [L-] = 0, можно
определить все константы устойчивости.
Влияние концентрации
карбонат-иона на коэффициент
распределения урана.
1 – дистиллированная вода;
2 – имитат морской воды,рН=8.

19. Влияние рН для случая поглотителя в форме катиона солевого фона

При изменении рН сорбат может участвовать в реакциях образования
моноядерных гидроксокомплексов. Процесс сорбции происходит в
соответствии с реакциями
z R Э M z Rz M zЭ
( z i ) R Э M (OH ) iz i Rz i M (OH ) i ( z i)Э
z 1
для случая лабильного сорбата
k b h
Kd
i 0
N
b h
i 0
i
i i
i
i
h → ∞ гидролиз подавлен и Kd → k0.
С уменьшением кислотности раствора
уравнение асимптоты к правой
ниспадающей ветви изотермы:
k z 1bz 1h ( z 1)
1 z 1 N
Kd
k
b
b
h
z
1
z
1
N
N
bN h
lg K d lg( k z 1bz 1bN 1 ) lg h 1 A ( 1) pH
N-z+1 = μ+1 - число несорбирующихся форм сорбата

20.

В условиях высокой ионной силы раствора сорбция положительно заряженных
форм сорбата подавлена, в межфазном распределении участвует только
нейтральный гидроксокомплекс M(OH)z0 в соответствии с реакцией
молекулярной сорбции.
k z bz h z
kb
Kd N
N z z
bi h i bi h z i
i 0
i 0
N
При h → ∞ Kd → 0, а в случае
b h
i 1
i
1
i
bi h N
i
lg Kd lg k z lg bz zpH
N 1
При h → 0 Kd → 0, а в случае
k z bz h z
1 z N
Kd
k
b
b
z z Nh
N
bN h
b h
i 0
i
lg K d lg( k z bz bN 1 ) lg h A pH
В случае инертного сорбата
Уравнение асимптоты к правой ветви имеет вид:
k z 1 bz 1bN 1
lg K d lg
( 1) pH
1 k z 1[m]

21. Влияние рН для случая поглотителя в Н+ форме

ki ( KiT aЭz i )aЭi z ki ' aЭi z
z
Принимая aЭ+ = aH+ ,
получим для лабильного сорбата
Kd
k 'a
i 0
i
N
lg K d lg z lg pH
Для правой ассимптоты:
lg K d lg lg bNT lg pH
z
ki ' biT f ( pH )
i 0
только для сильнокислотного катионита.
b a
T i
b
i aH
i 0
Для левой ассимптоты:
i z T
H i
i
H
z
k 'b
i 0
N
i
T
i
T z i
b
i aH
i 0

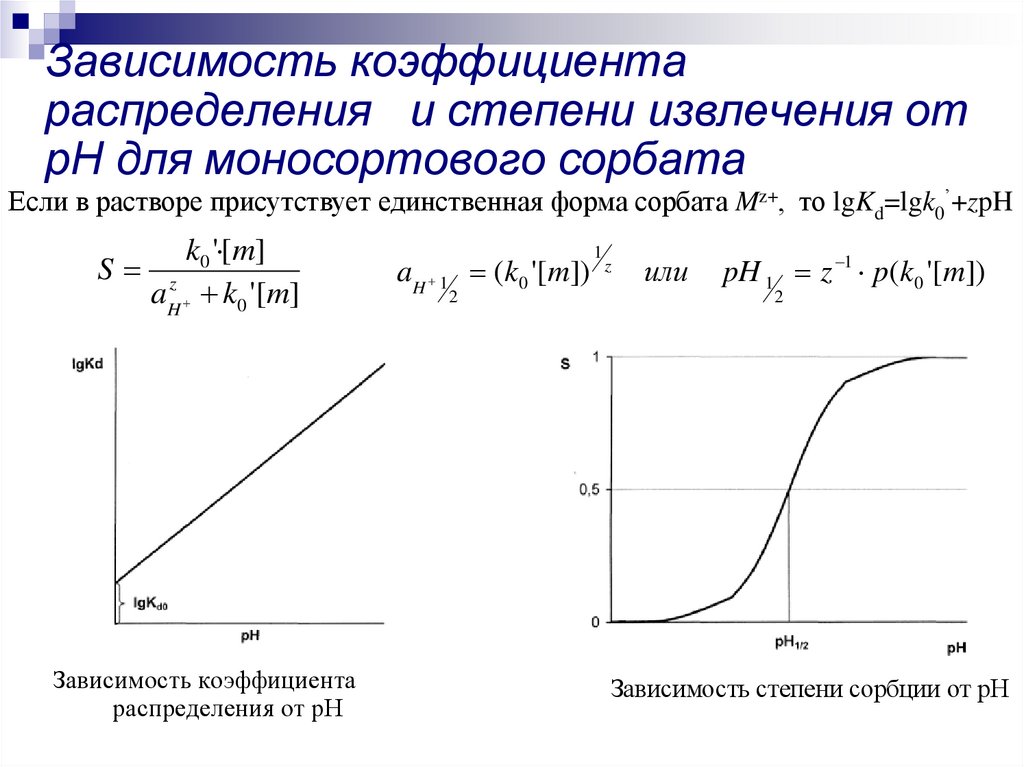
22. Зависимость коэффициента распределения и степени извлечения от рН для моносортового сорбата

Если в растворе присутствует единственная форма сорбата Mz+, то lgKd=lgk0’+zpH
k0 ' [m]
S z
aH k0 '[m]
Зависимость коэффициента
распределения от рН
aH 1 (k0 '[m])
2
1
z
или
pH 1 z 1 p(k0 '[m])
2
Зависимость степени сорбции от рН

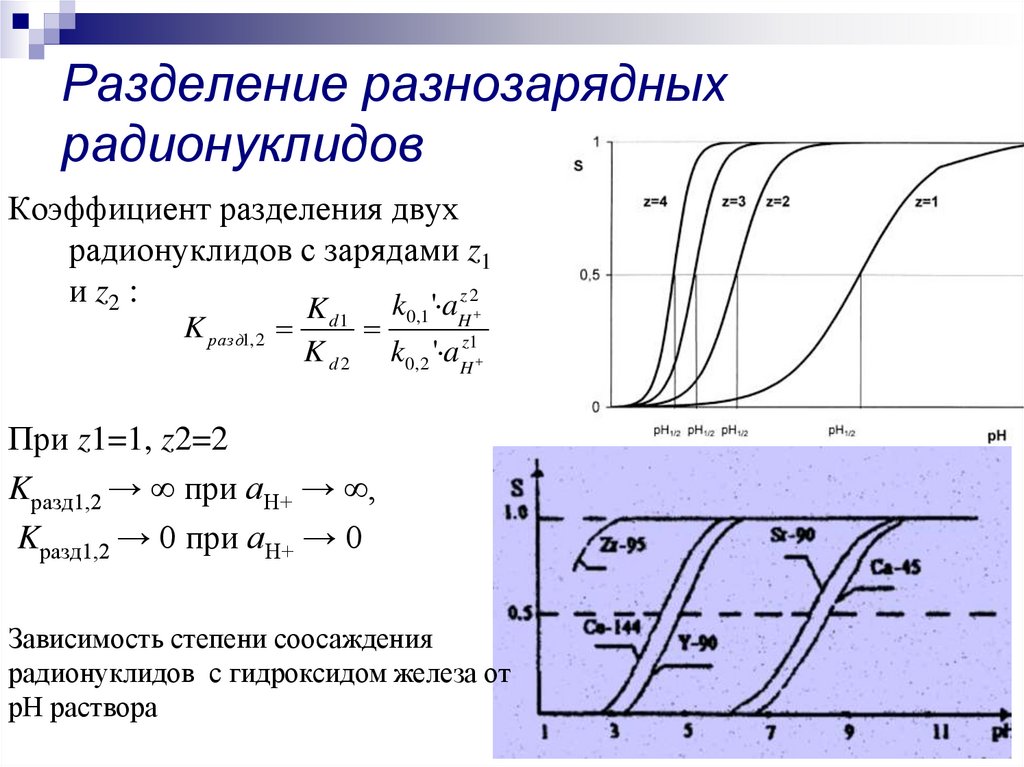
23. Разделение разнозарядных радионуклидов

Коэффициент разделения двух
радионуклидов с зарядами z1
z2
и z2 :
k
'
a
K
K разд1, 2
d1
Kd2
0,1
H
z1
H
k0, 2 ' a
При z1=1, z2=2
Kразд1,2 → ∞ при аН+ → ∞,
Kразд1,2 → 0 при аН+ → 0
Зависимость степени соосаждения
радионуклидов с гидроксидом железа от
рН раствора

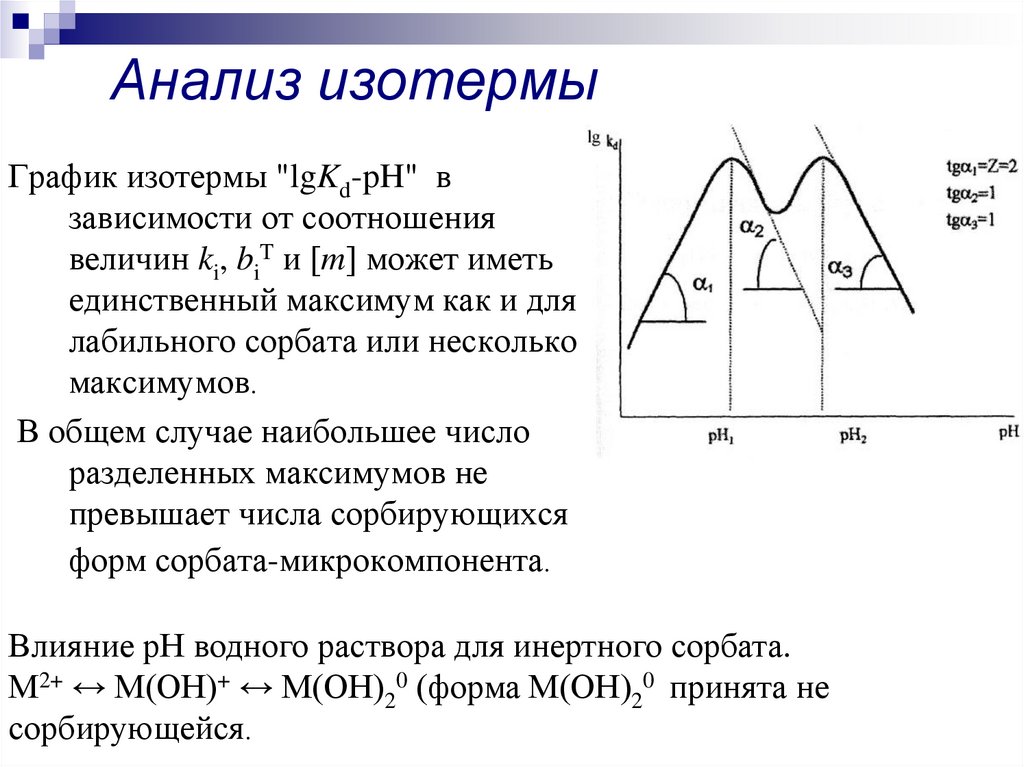
24. Анализ изотермы

График изотермы "lgKd-pH" в
зависимости от соотношения
величин ki, biT и [m] может иметь
единственный максимум как и для
лабильного сорбата или несколько
максимумов.
В общем случае наибольшее число
разделенных максимумов не
превышает числа сорбирующихся
форм сорбата-микрокомпонента.
Влияние рН водного раствора для инертного сорбата.
М2+ ↔ М(ОН)+ ↔ М(ОН)20 (форма М(ОН)20 принята не
сорбирующейся.

25. Выводы

Проанализировано влияние концентрации сорбата.
Показано, что в случае сорбции микрокомпонентов
выполняется изотерма Генри.
Анализ изотермы сорбции показывает, что на вид
изотермы влияет неоднородность сорбента и сорбата.
Проведен анализ влияния удельной массы сорбента на
изотерму сорбции
Показано, что в случае моносортового или сложного
лабильного сорбата изотерма сорбции «lgε - lg[m]»
представляет собой прямую dlgε /dlg[m] =1. Нарушение
этого признака dlgε /dlg[m] <1 является однозначным
свидетельством инертности системы форм состояния.

26. Выводы

Показано влияние концентрации фонового электролита,
лиганда, рН раствора на статику сорбции.
В случае сильнокислотного катионита или
молекулярной сорбции изотермы "lgKd - pH" для
лабильного сорбата представляют собой кривую с
единственным максимумом, положение которого
соответствует величине рH изоэлектрической точки
системы гидроксокомплексов сорбата M(OH)iz-i и не
зависит от свойств сорбента. В случае инертного сорбата
изотермы "lgKd - pH" могут иметь несколько точек
экстремума, количество которых определяется числом
сорбирующихся форм сорбата.
Предложены условия разделения радионуклидов.

27. Библиографический список

Несмеянов А.Н. Радиохимия/ А.Н. Несмеянов. М.:Химия, 1979.
559с.
Вольхин В.В. Неорганические сорбенты/ В.В. Вольхин, Ю.В.
Егоров, Ф.А. Белинская и др.// Ионный обмен. М.: Наука.
1981. 271 с.
Егоров
Ю.В.
Статика
сорбции
микрокомпонентов
оксигидратами/ Ю.В. Егоров. М.: Атомиздат. 1975. 198 с.
Инцеди Я. Применение комплексов в аналитической химии/ Я.
Инцеди. М.: Мир. 1979. 376 с.