Дифференциальные уравнения

1. Дифференциальные уравнения

Основные понятия

2. Дифференциальные уравнения.

Задача о первообразной.
Найти функцию
y (x)
такую, что
y f (x)
Решение.
y ( x)
f ( x)dx F ( x) C

3. Дифференциальные уравнения.

Задача о движении.
Материальная точка движется вдоль оси ОХ
со скоростью V(t). Найти закон движения x(t).
Решение.
Скорость движения - x (t )
Поэтому
x V (t )
Тогда
где
x(t ) V (t )dt F (t ) C
F (t ) - первообразная.
Пусть
t t o , x xo
x o F (t o ) C ,
т о ест ь C xo F (to )
x (t ) F (t ) F ( t o ) x o

4. Дифференциальные уравнения.

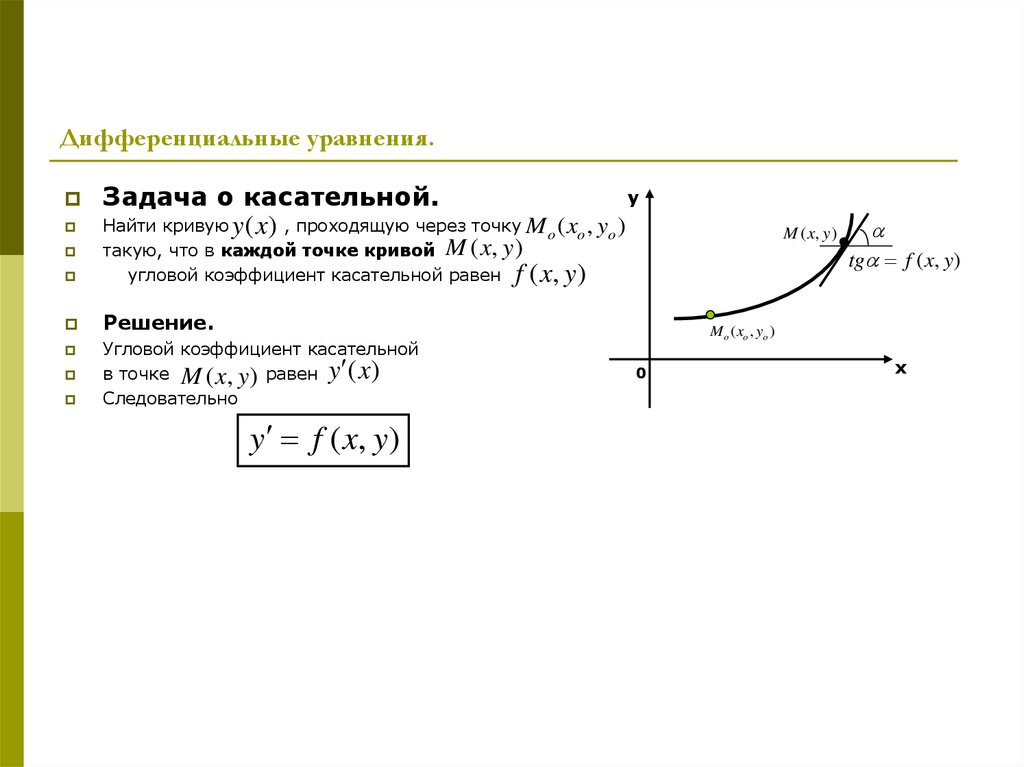
y
Задача о касательной.
Найти кривую y (x) , проходящую через точку M o ( xo , yo )
такую, что в каждой точке кривой M ( x, y )
угловой коэффициент касательной равен f
Решение.
Угловой коэффициент касательной
в точке M ( x, y ) равен y (x )
Следовательно
y f ( x, y)
M ( x, y )
( x, y)
tg f ( x, y)
M o ( xo , yo )
0
x

5. Дифференциальные уравнения.

Определение 1.
Дифференциальным уравнением порядка n
называется уравнение вида
F ( x, y, y , , y(n) ) 0
Определение 2.
Порядком дифференциального уравнения
называется порядок старшей производной,
входящей в уравнение.
Определение 4.
(1)
Решением дифференциального уравнения (1)
называется функция y (x) , которая
удовлетворяет уравнению, то есть
F ( x, ( x), ( x), , (n) ( x)) 0
при
x (a , b)
Определение 3.
Уравнение вида
y (n) f ( x, y, y , , y ( n 1) )
называется уравнением,
разрешенным относительно
старшей производной.
В частности:
при n=1
y f ( x, y)
(2)

6. Дифференциальные уравнения.

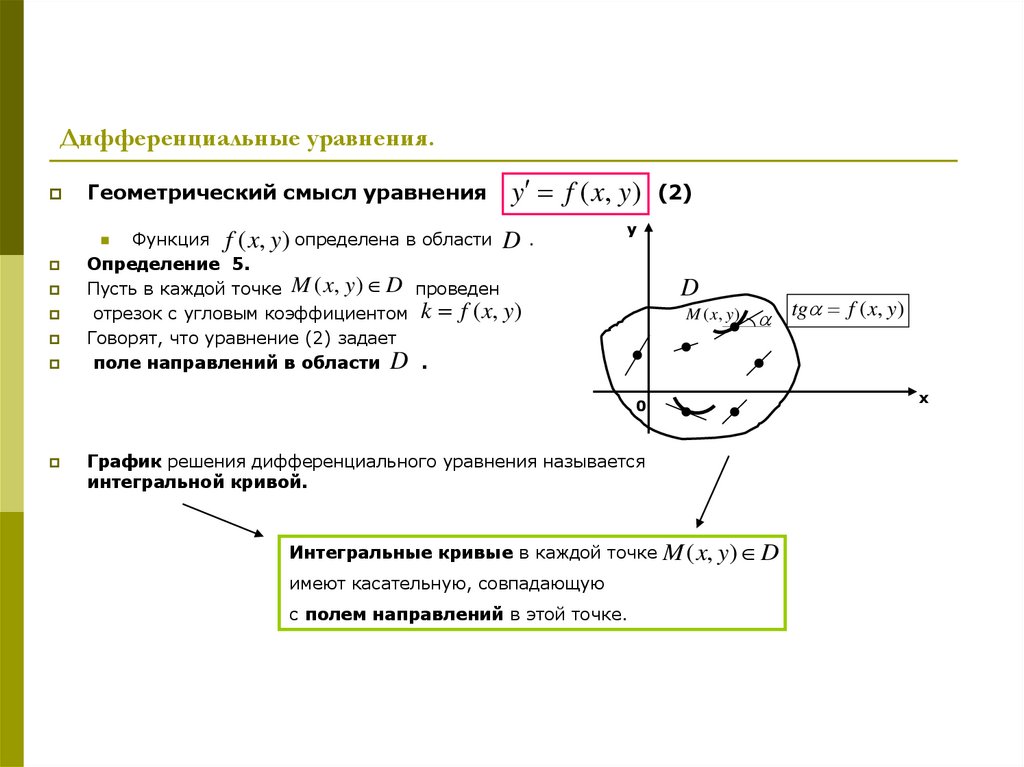
Геометрический смысл уравнения
y f ( x, y )
Функция f ( x, y ) определена в области D .
Определение 5.
Пусть в каждой точке M ( x, y ) D проведен
отрезок с угловым коэффициентом k f ( x, y)
Говорят, что уравнение (2) задает
поле направлений в области D .
(2)
y
D
M ( x, y )
tg f ( x, y)
х
0
График решения дифференциального уравнения называется
интегральной кривой.
Интегральные кривые в каждой точке
имеют касательную, совпадающую
с полем направлений в этой точке.
M ( x, y) D

7. Дифференциальные уравнения.

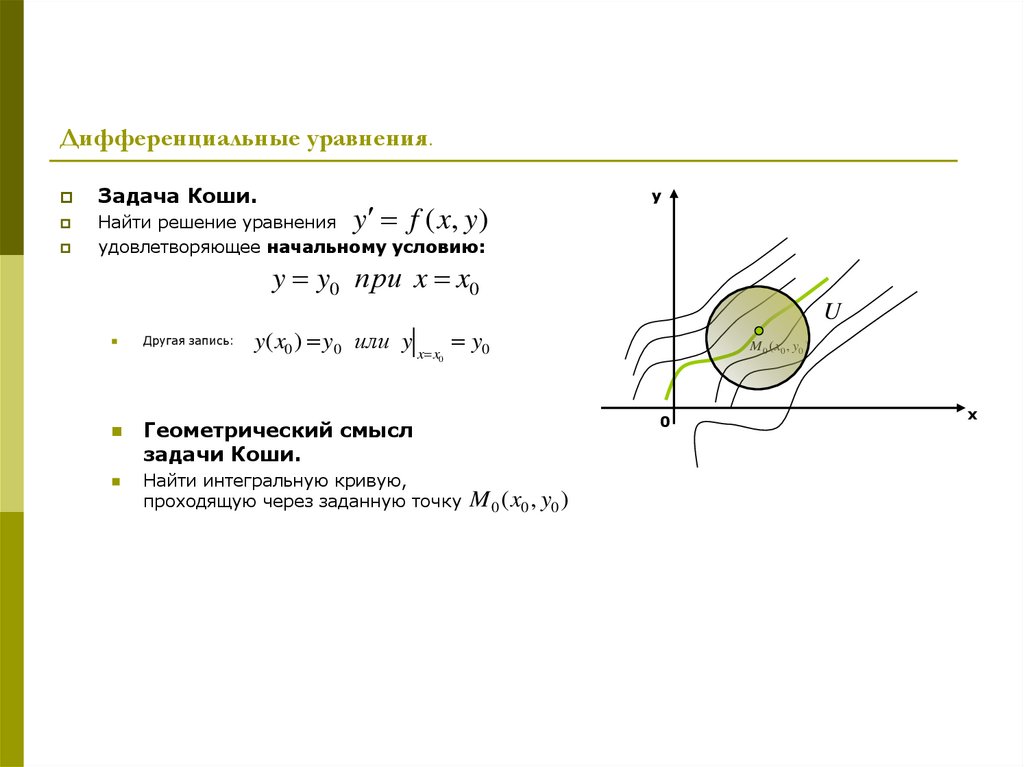
Задача Коши.
y f ( x, y)
y
Найти решение уравнения
удовлетворяющее начальному условию:
y y0 при x x0
U
Другая запись:
y( x0 ) y 0 или y x x y0
M 0 ( x0 , y0 )
0
0
Геометрический смысл
задачи Коши.
Найти интегральную кривую,
проходящую через заданную точку
M 0 ( x0 , y0 )
x

8. Дифференциальные уравнения.

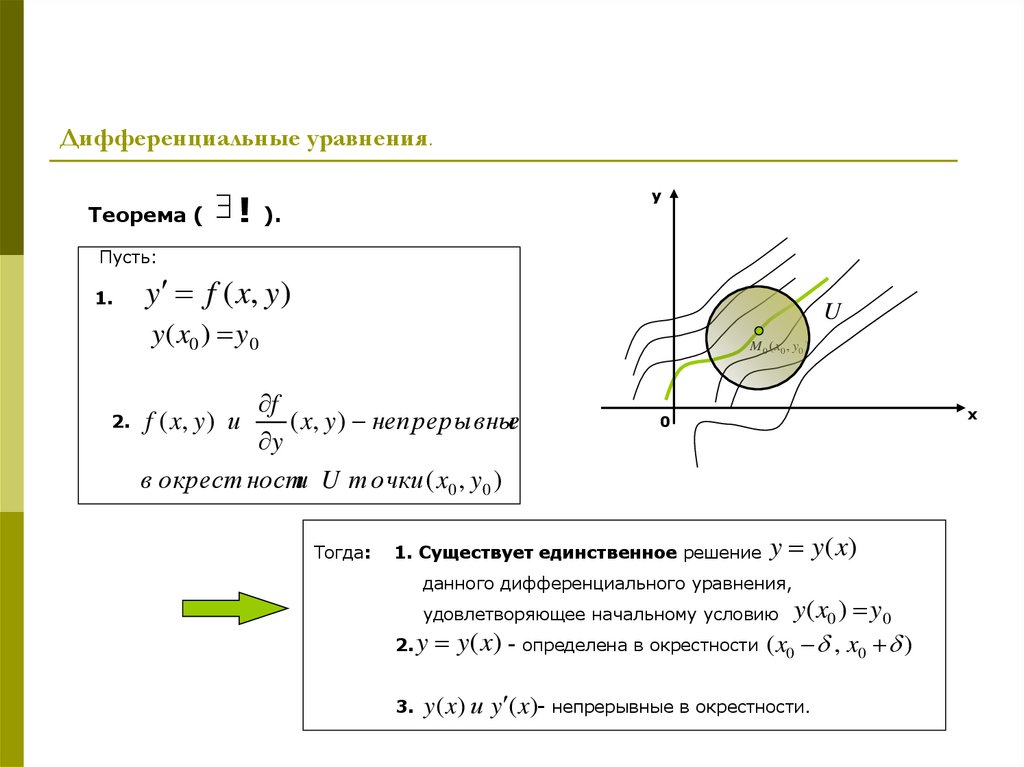
Теорема (
!
y
).
Пусть:
1.
y f ( x, y)
U
y( x0 ) y 0
2.
M 0 ( x0 , y0 )
f
( x, y ) непрерывные
y
в окрест ности U т очки ( x0 , y0 )
f ( x, y ) и
Тогда:
x
0
1. Существует единственное решение
y y(x)
данного дифференциального уравнения,
y( x0 ) y 0
2. y y(x) - определена в окрестности ( x0 , x0 )
удовлетворяющее начальному условию
3.
y( x) и y ( x)- непрерывные в окрестности.

9. Дифференциальные уравнения.

Пример 2.
Найти решение уравнения
y y x,
удовлетворяющее заданному начальному условию:
a) y (0) 1 , b) y(0) 2
(Решить две задачи Коши).
Решение.
Данное уравнение является линейным уравнением первого
порядка. y x 1 Ce x
Оно интегрируется в квадратурах:
Решение задачи Коши имеет вид:
в случае a) y x 1 ,
в случае b) y ( x 1) e x ,
(C 0)
( C 1)

10. Дифференциальные уравнения.

Определение.
y f ( x, y)
Общим решением дифференциального уравнения
в области D называется функция y ( x, C )
, зависящая от х
и произвольной постоянной С, непрерывная, имеющая непрерывные
частные производные, и удовлетворяющая условиям:
1) при любых значениях С , таких что точка ( x, ( x, C )) D ,
функция y ( x, C ) является решением
дифференциального уравнения;
2) при любых ( x0 , y0 ) D найдется такое значение
,
~
что решение y ( x, C ) удовлетворяет начальному условию y ( x0 )
~
C C
Решение, полученное из общего решения при конкретном значении С,
называется частным решением.
y0

11. Дифференциальные уравнения.

Пример.
y cos x y cos xdx sin x C
y sin x C общее решение Д . У .
C 0 y sin x
C 1 y sin x 1
C
1
1
y sin x
2
2
Частные
решения Д.У.

12. Дифференциальные уравнения.

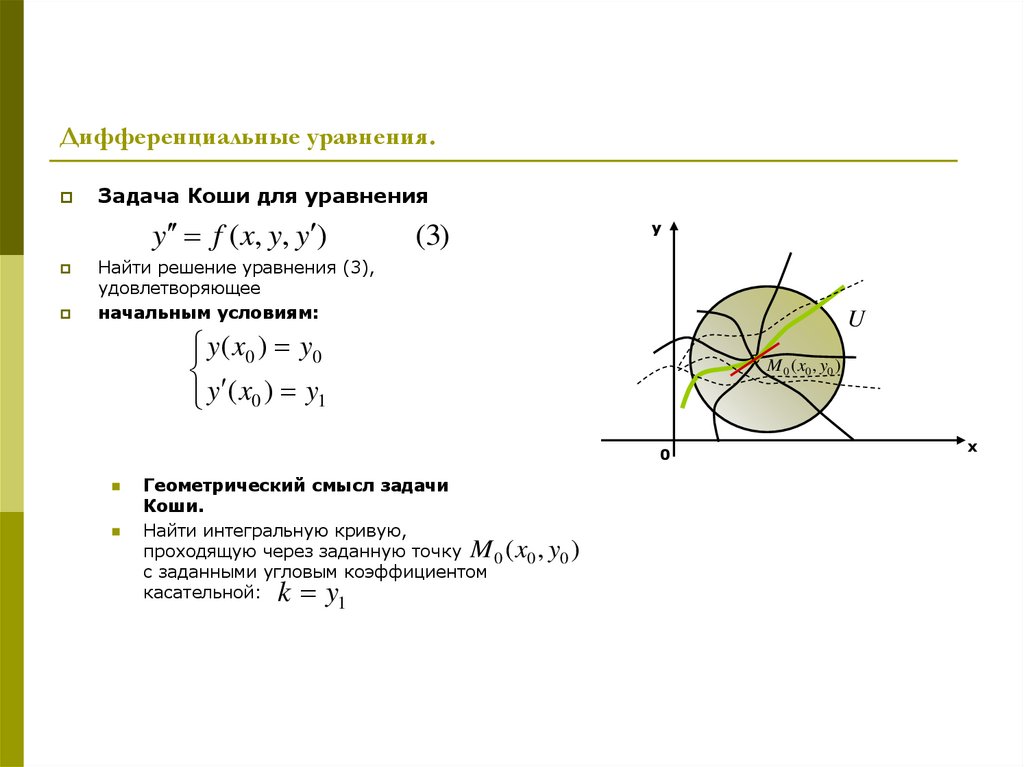
Задача Коши для уравнения
y f ( x, y, y )
(3)
y
Найти решение уравнения (3),
удовлетворяющее
начальным условиям:
U
y ( x0 ) y0
y ( x0 ) y1
M 0 ( x0 , y0 )
0
Геометрический смысл задачи
Коши.
Найти интегральную кривую,
проходящую через заданную точку M 0 ( x0 , y0 )
с заданными угловым коэффициентом
касательной:
k y1
x

13. Дифференциальные уравнения.

Теорема (
Пусть;
1.
! ).
y f ( x, y, y ),
y ( x0 ) y0 ,
y ( x ) y .
0
1
2.
f
f
( x, y, y ) ,
( x, y, y )
y
y
непрерывные функции в
f ( x, y, y ) ,
окрест ности U т очки ( xo , y0 , y1 )
Тогда:
1. Существует единственное
решение y y(x) данного
дифференциального уравнения,
удовлетворяющее начальным
условиям;
2. y y(x)
окрестности
3.
определена в
( x0 , x0 )
y ( x) , y ( x) , y ( x)
непрерывны е функции .

14. Дифференциальные уравнения.

Определение.
Общим решением дифференциального
уравнения y f ( x , y , y )
называется функция y ( x , C1 , C2 ) ,
зависящая от х и двух произвольных
постоянных C1 и C 2
таких,
что при каждых значениях C1 и C 2
функция y ( x , C1 , C 2 )
является решением данного
дифференциального уравнения.
Решение, полученное из общего решения
при конкретных значениях C1 и C 2 ,
называется частным решением
дифференциального уравнения..