Конденсаторы. Электрическая емкость

1. Конденсаторы Электрическая емкость

При сообщении проводнику заряда, на его
поверхности появляется потенциал φ. Но если этот же
заряд сообщить другому проводнику, то потенциал
будет другой. Это зависит от геометрических
параметров проводника. Но в любом случае, потенциал
φ пропорционален заряду q.
q = Cφ
Коэффициент пропорциональности называют электроемкостью.
Электроемкость – физическая величина, численно
равная заряду, который необходимо сообщить
проводнику для того, чтобы изменить его потенциал
на единицу.
• Единица измерения емкости в СИ – фарада (1 Ф = 1Кл / 1В).

2.

Если потенциал поверхности шара
то
q
φшар.
4πεε0 R
Cшар. = 4 πεε0R
• Если ε = 1 (воздух, вакуум) и R = R земли, то
CЗ = 7·10 –4 Ф или 700 мкФ.
Чаще на практике используют и более мелкие
единицы: 1 нФ (нанофарада) = 10 –9 Ф и 1 пкФ
(пикофарада) = 10 –12 Ф.
Конденсатор – устройство
электрического заряда.
для
накопления

3.

Электростатическое поле будет сосредоточено
внутри конденсатора между обкладками.
Конденсаторы бывают плоские, цилиндрические и сферические.
Заряды на обкладках противоположны по знаку, но одинаковы
по величине.
Емкость конденсатора:
q
q
C
φ1 φ2 U

4.

Найдем формулу для емкости плоского конденсатора.
Напряженность между обкладками равна
σ
q ,
E
ε0 ε
ε0 εS
где: S – площадь пластин (обкладок); q – заряд конденсатора
qd отсюда
U Ed
.
0 S
,
q ε0 εS
C
U
d
ε – диэлектрическая проницаемость диэлектрика между
обкладками.
Диэлектрическая проницаемость вещества очень сильно влияет
на емкость конденсатора.

5. Соединение конденсаторов

Емкостные батареи – комбинации параллельных и
последовательных соединений конденсаторов.
1) Параллельное соединение
Общим является напряжение U
q1 = C1U;
q2 = C2U;
Суммарный заряд:
q = q1 + q2 = U(C1 + C2)
Результирующая емкость:
q
C C1 C 2
U

6.

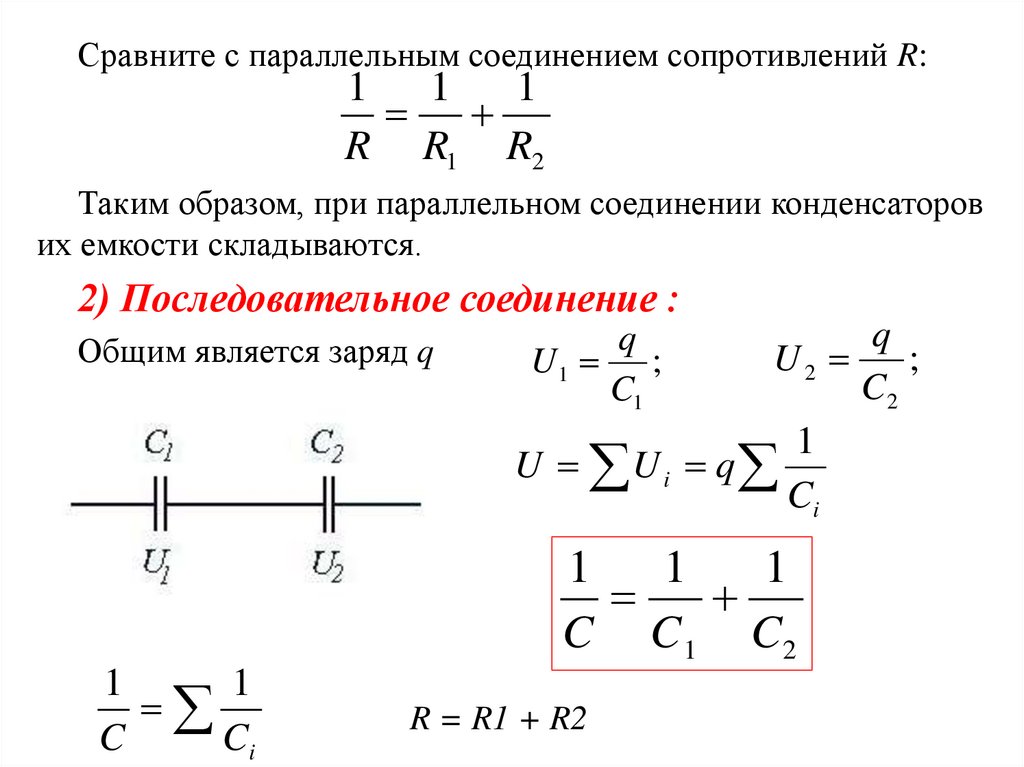
Сравните с параллельным соединением сопротивлений R:
1 1
1
R R1 R2
Таким образом, при параллельном соединении конденсаторов
их емкости складываются.
2) Последовательное соединение :
Общим является заряд q
q
U2
;
C2
1
U U i q
Ci
q
U1 ;
C1
1
1
1
C C 1 C2
1
1
C
Ci
R = R1 + R2

7. Расчет емкостей различных конденсаторов

1. Емкость плоского конденсатора.
x1
σ
E
;
φ1 φ2 Edx
d
0
ε0 ε
x2
где
d = x2 – x1 – расстояние между
,
пластинами.
Так как заряд q σS , то
q
S
C
ε0 ε
φ1 φ2
d

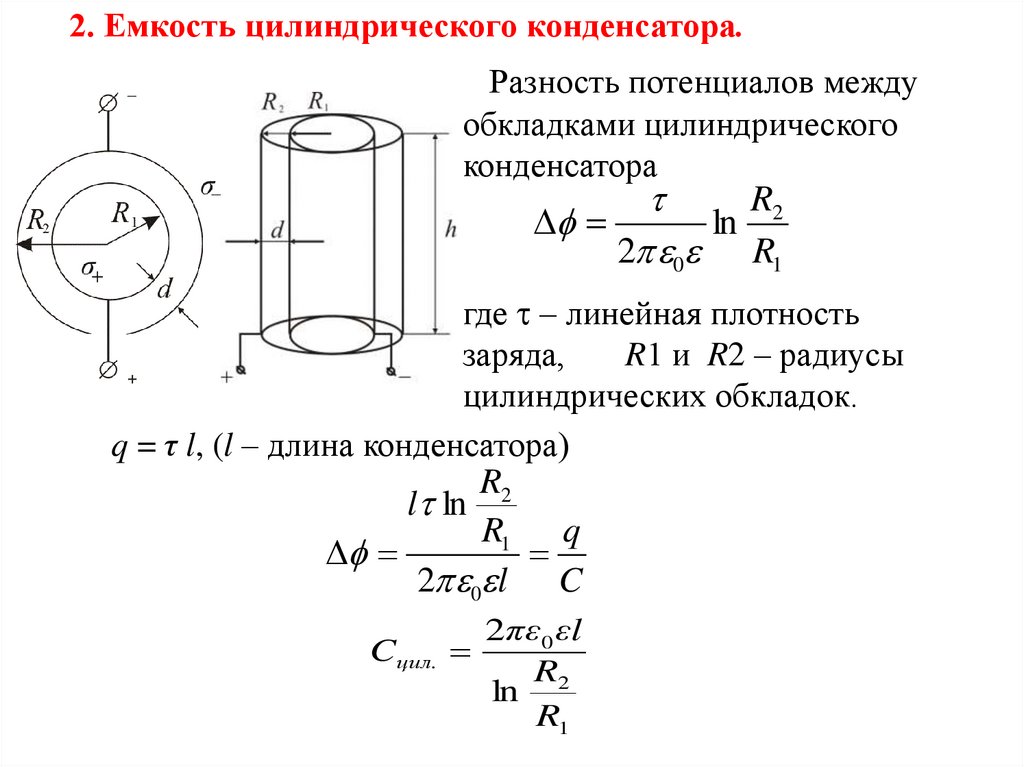
8.

2. Емкость цилиндрического конденсатора.
Разность потенциалов между
обкладками цилиндрического
конденсатора
R2
ln
2 0 R1
где – линейная плотность
заряда,
R1 и R2 – радиусы
цилиндрических обкладок.
q = τ l, (l – длина конденсатора)
R2
l ln
R1 q
Δ
2 0 l C
Cцил.
2πε0 εl
R2
ln
R1

9.

Понятно, что зазор между обкладками мал: d = R2 – R1, то есть
d << R1, тогда
R
R R1
ln 2 2
R1
R1
Cцил.
2πε0 εlR1
S
ε0 ε
R2 R1
d
3. Емкость сферического конденсатора.
q 1
1
φ1 φ2
4πε0ε R1 R2
Это разность потенциалов между обкладками
конденсатора, где R1 и R2 – радиусы
q
,
C
4πε0 εR1R2
C
R2 R1

10.

В сферическом конденсаторе R1 ≈ R2; S = 4πR2; R2 – R1 = d –
расстояние между обкладками. Тогда
4 0 R
S
0 .
d
d
2
Cшар.
Таким образом, емкость сферического конденсатора
Сшар.
S
ε0 ε ,
d
что совпадает с емкостями плоского и цилиндрического
конденсаторов.

11. Энергия заряженного конденсатора

CU
Wc
2
2
Энергию конденсатора можно посчитать и по другим
формулам:
2
q
1
Wc
qU
2C 2