Похожие презентации:
Стохастические модели ошибок датчиков первичной информации для авиационных приборов и систем
1.
2.3.4 Стохастические модели ошибокдатчиков первичной информации для
авиационных приборов и систем
2.
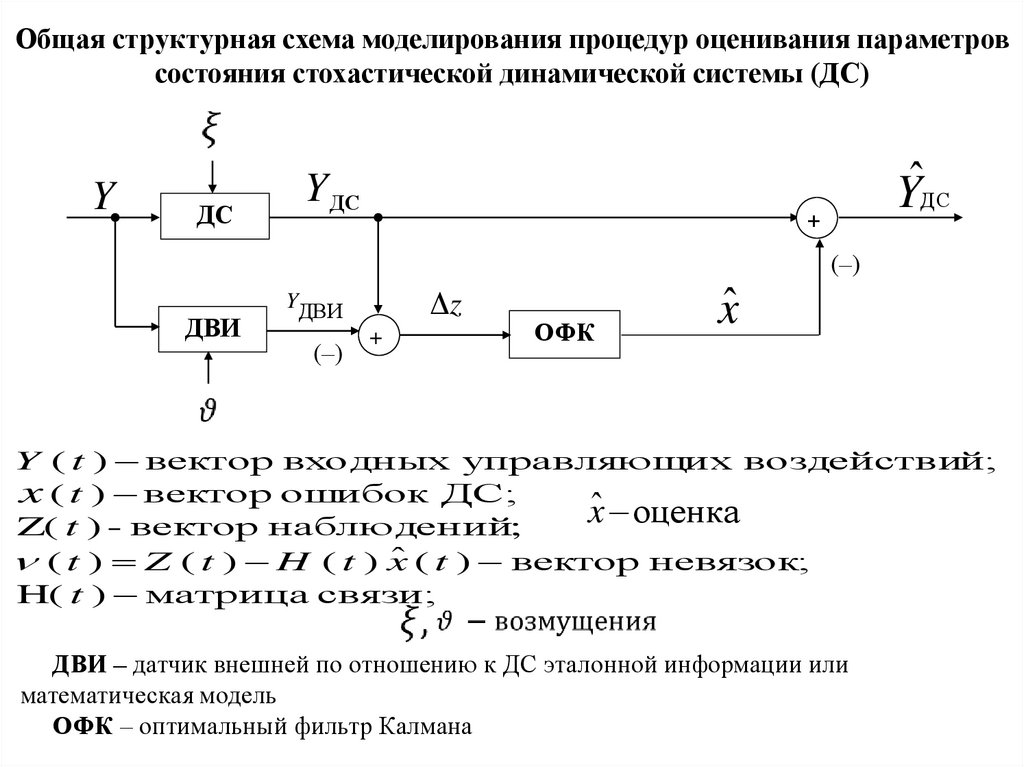
Общая структурная схема моделирования процедур оценивания параметровсостояния стохастической динамической системы (ДС)
Y
ДС
Y ДС
YˆДС
+
(–)
ДВИ
Δz
YДВИ
(–)
+
ОФК
x̂
Y ( t ) вектор входных управляющи х воздействий;
x ( t ) вектор ошибок ДС;
ˆ оценка
x
Z( t ) - вектор наблюдений;
ˆ ( t ) вектор невязок;
(t ) Z (t ) H (t ) x
H( t ) матрица связи;
ДВИ – датчик внешней по отношению к ДС эталонной информации или
математическая модель
ОФК – оптимальный фильтр Калмана
3.
Алгоритм ОФК для последовательной обработки элементов векторанаблюдений z i [ z 1( i ) z j ( i ) z l ( i ) ] T (для него написана программа на языке С++)
Прогноз:
m0 xˆi / i 1 Фi xˆi 1 / i 1
M 0 Pi / i 1 Φ i Pi 1/ i 1 Φ Ti i Q i 1 iT
Коррекция:
ν j z j Н j m j 1
j H j M j 1 H Tj R j
K j М j 1 H Tj / j
m j m j 1 K j j
M j M j 1 K j H j M j 1;
xˆi / i ml ;
j 1, l
Pi / i M l
Задача: сформировать модели датчиков первичной пилотажно-навигационной
информации.
4.
При построении моделей датчиков первичной информации (ДПИ) считаетсявозможным описание их ошибок в виде двух составляющих: систематической
с и чисто случайной , распределенной по нормальному закону. Например,
погрешности акселерометра a~ ( t ) или гироскопа ω(t ) могут быть
представлены в следующем виде:
~(t ) a
~ (t ) ξ(t )σ(t )
a
c
(2.48)
ξ (t ) N (0, 1)
- случайная величина, имеющая
нормальное распределение с математическим ожиданием “0” и дисперсией “1”.
σ(t ) - коэффициент, характеризующий интенсивность случайного процесса
(СКО).
Модель погрешности (2.48) может быть сформирована с использованием
формирующего фильтра, схема которого имеет вид
(P)
W(P)
a~( P)
Здесь P – оператор Лапласа. Для моделирования ДПИ необходимо найти
передаточную функцию W(P).
5.
Моделируемый выходной сигнал формирующего фильтраможно приближенно описать, используя следующие
корреляционные функции
- экспоненциальная
t /T
~
~
2
K ( t ) M [ a ( t ) a ( t T )] σ e
- экспоненциально-косинусная
α t
2
K (t ) σ e
cosβt
где Т – время корреляции погрешности;
1
T
σ(t ) σ const
K (0) σ 2
Нормированная корреляционная функция
r (t ) K (t ) / K (0) K (t ) / σ 2
β
- круговая частота
6.
Типовые нормированные корреляционные функцииКорреляционные функции ошибки акселерометра:
re
- вычисленная по экспериментальным данным;
ra
1
- полученная путем экспоненциальной аппроксимации;
ra
2
rm
- полученная путем экспоненциально-косинусной аппроксимации;
- учтенная априорно в модели.
7.
2.3.4.1Модели ошибок ДПИ при экспоненциальной корреляционной
функции
Спектральная плотность процесса имеет вид
S ( )
K ( )e
j
d
2
e
e
j
d
(2.49)
8.
Выражение (2.49) может быть представлено в развернутом виде( j )
e
2
( j )
2
( j )
2
S ( ) e
d e
d
j
0
0
σ
2
1
1
α jω α j ω
0
e
0
( j )
j
2
2σ α
α
2
ω
(2.50)
2
S а~ (ω)
Спектральные плотности входного Sξ (ω) 1 и выходного
сигналов в модели ДПИ связаны между собой через модуль частотной
передаточной функции
формирующего фильтра:
W ( jω)
S a~ (ω) W ( jω) S ξ (ω)
2
Поэтому для нашего случая справедливо соотношение
2σ 2α
W ( jω) S a~ ( ) 2
α ω2
2
(2.51)
9.
Спектральной плотности (2.51) можно поставить в соответствие передаточнуюфункцию W ( j ) . Можно показать, что такая передаточная функция имеет вид
W ( j ) 2 2 /( j )
(2.52)
Это следует из следующего равенства и определения модуля передаточной
функции:
2 2 ( j )
2 2 ( j )
2 2
( j ) ( j )
jV
W(jω)=U(ω)+jV(ω)
U
W ( jω) A(ω) U 2 (ω) V 2 (ω) - АЧХ
ψ(ω)
A(ω)
ψ(ω) arctg
V (ω )
- ФЧХ
U (ω )
10.
22σ 2 (α jω)
2σ 2 α
2
2
2
α ω
α ω2
(2.53)
Записывая передаточную функцию (2.52) в форме Лапласа,
получим
2σ 2 α a~ ( P)
W ( P)
p α
ξ ( P)
11.
Таким образом, на вход формирующего фильтра поступает белый шум, а навыходе получается автокоррелированный процесс. Из соотношения (2.53)
получаются уравнения, описывающие динамику изменения смещения
~(t )
акселерометра a
в операторной форме и во временной области:
~
a ( P )( p α ) ξ ( P ) σ 2 α
(2.54)
~
а (t ) α a~ (t ) ξ(t ) σ 2α
(2.55)
Аналогичным уравнением для приближения первого порядка может быть
описан угловой дрейф гироскопа. Такая модель легко отображается на общую
модель ошибок динамической системы
xμ (t ) Aμ (t ) xμ (t ) Gμ (t )ξ μ (t )
где
Aμ (t ) αμ
;
Gμ (t ) σμ 2αμ
1
;
T
- индекс, обозначающий акселерометр;
μ a~
гироскоп.
(2.56)
;
x
- индекс, обозначающий
12.
Генераторслучайных
чисел,
имеющих
гауссовское
распределение
σx
×
x(t0 )
2
x
×
x
+
×
x
13.
2.3.4.2Модели ошибок ДПИ при экспоненциально-косинусной
корреляционной функции
Спектральная плотность процесса имеет вид
S (ω) K ( )e jωτd σ 2 e
α τ
σ2α(b2 ω2 )
,
b4 2(α2 β2 )ω2 ω4
где b 2 α 2 β 2 ;
T - время корреляции
1
T
cos βτe jωτd
(2.57)
14.
Спектральной плотности (2.57) можно поставить в соответствие передаточнуюфункцию
W ( p)
2σ 2 α ( p b)
p 2 2 αp b 2
~
a ( p )
ξ( p)
(2.58)
Отсюда уравнение, описывающее динамику изменения смещения сигнала
акселерометра в операторной форме, будет иметь вид
функции:
~
(2.59)
( p 2 2 αp b 2 ) a ( p ) ξ ( p ) σ 2 α ( p b )
Выражению (2.59) соответствует следующая система уравнений во временной
области
~
(2.60)
a ( t ) a ( t ) ξ ( t ) σ 2 α
~
~
a ( t ) b 2 a ( t ) 2 α a ( t ) ξ ( t ) σ 2 α ( b 2 α )
(2.61)
В уравнениях (2.60), (2.61) параметр a (t ) является вспомогательной переменной,
~
a ( t ) – суммарная ошибка акселерометра.
15.
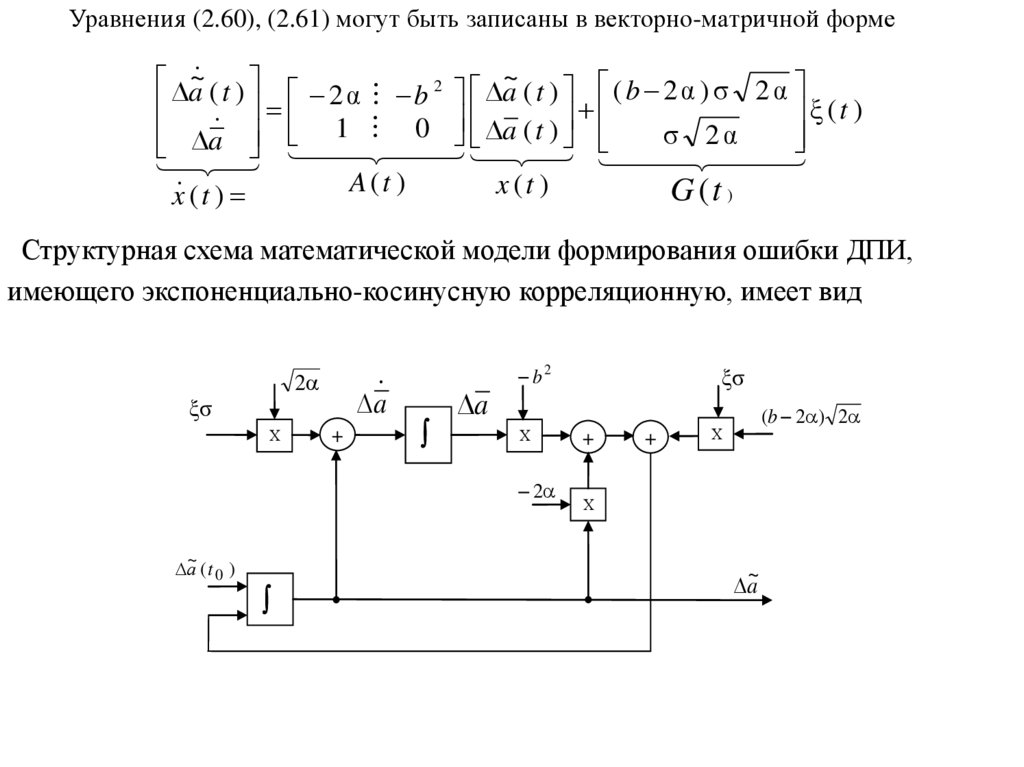
Уравнения (2.60), (2.61) могут быть записаны в векторно-матричной формеa~ ( t ) 2 α b 2 a~ ( t ) ( b 2 α ) σ 2 α
ξ (t )
a ( t )
1
0
σ 2α
a
A(t )
x(t )
G (t )
x ( t )
Структурная схема математической модели формирования ошибки ДПИ,
имеющего экспоненциально-косинусную корреляционную, имеет вид
2
ξσ
Х
a
+
a
b2
Х
2
~
а ( t 0 )
ξσ
+
+
(b 2 ) 2
Х
Х
~
a













 Физика
Физика








