Статистическая радиотехника. Спектральный метод анализа прохождения стационарного случайного процесса через линейную цепь

1. Курс лекций по дисциплине «СТАТИСТИЧЕСКАЯ РАДИОТЕХНИКА»

Лектор - Куроедов Сергей
Константинович
Лекция 6

2. ПЛАН ЛЕКЦИИ 6

1. Спектральный метод анализа прохождения
стационарного случайного процесса через
линейную цепь
2. Корреляционная характеристика цепи,
корреляционный метод анализа
прохождения стационарного случайного
процесса через линейную цепь
3. Дифференцирование случайных процессов
4. Интегрирование случайных процессов
5. Источники шумов в радиотехнических цепях
6. Корреляционный метод анализа
прохождения случайного процесса через
линейную нестационарную цепь

3. ПЛАН ЛЕКЦИИ 4

7. Характеристики безынерционной
нестационарной цепи
8. Анализ прохождения детерминированного
сигнала через безынерционную цепь со
случайным коэффициентом передачи
9. Анализ прохождения случайного процесса
через безынерционную параметрическую
цепь и цепь со случайным коэффициентом
передачи
10. Преобразование закона распределения
случайного процесса в нелинейной
безынерционной цепи
11. Корреляционный метод анализа
прохождения случайного процесса через
нелинейную цепь

4.

СЛУЧАЙНЫЕ ПРОЦЕССЫ В ЛИНЕЙНЫХ
СТАЦИОНАРНЫХ ЦЕПЯХ
y(t)
x(t)
Sx(ω)
K(jω)
Sy(ω)
Реализация выходного процесса:
y (t ) S y ( ) K ( j ) S x ( )

5.

Спектр мощность выходного процесса:
1
2
W y ( ) lim K ( j ) S x ( )
T T
1
2
2
K ( j ) lim S x ( )
T T
1
2
2
lim S x ( ) Wx ( ), K ( j ) K P ( )
T T

6.

СПЕКТРАЛЬНЫЙ МЕТОД АНАЛИЗА
ПРОХОЖДЕНИЯ СЛУЧАЙНЫХ ПРОЦЕССОВ
ЧЕРЕЗ ЛИНЕЙНЫЕ СТАЦИОНАРНЫЕ ЦЕПИ
Wy ( ) K P ( )Wx ( )
Корреляционная характеристика цепи –
автокорреляционная функция
импульсной характеристики цепи
Rh ( ) (h, h ) h(t )h(t )dt
h(t ) K ( j ), h(t ) K ( j )e
j

7.

СВЯЗЬ КОЭФФИЦИЕНТА ПЕРЕДАЧИ
МОЩНОСТИ И КОРРЕЛЯЦИОННОЙ
ХАРАКТЕРИСТИКИ ЦЕПИ
1
Rh ( )
2
1
2
K ( j ) K ( j )e
d
j
K ( j )K
( j ) e
j
1
d
2
K
P
( )e
j
d
Rh ( ) K P ( )
Корреляционная характеристика и
коэффициент передачи мощности цепи
связаны парой преобразований Фурье

8.

КОРРЕЛЯЦИОННЫЙ МЕТОД АНАЛИЗА
ПРОХОЖДЕНИЯ СЛУЧАЙНЫХ ПРОЦЕССОВ
ЧЕРЕЗ ЛИНЕЙНЫЕ СТАЦИОНАРНЫЕ ЦЕПИ
1
R y ( )
2
K
P
( )Wx ( )e
j
d
K P ( ) Rh ( ), Wy ( ) Rx ( )
R y ( )
R ( ) R ( )d R ( ) R ( )
x
h
x
h
Функция корреляции выходного процесса
определяется сверткой функции корреляции
входного процесса и корреляционной
характеристики цепи

9.

ДИФФЕРЕНЦИРОВАНИЕ СЛУЧАЙНЫХ
ПРОЦЕССОВ
Математическое ожидание:
dx(t )
y (t )
d x(t )
0
dt my y(t )
dt
Функция корреляции выходного процесса:
mx 0
R y ( ) y (t ) y (t )

10.

ФУНКЦИЯ КОРРЕЛЯЦИИ РЕЗУЛЬТАТА
ДИФФЕРЕНЦИРОВАНИЯ
x(t t ) x(t ) x(t t ) x(t )
R y ( ) lim
t 0
t
t
2 Rx ( ) Rx ( t ) Rx ( t )
lim
R
( )
x
2
t 0
t
Дисперсия:
Спектр
мощности:
Ry (0) Rx (0)
2
y
Rx ( ) Wx ( )
R y ( ) Rx ( ) ( j ) Wx ( )
2

11.

СПЕКТР МОЩНОСТИ РЕЗУЛЬТАТА
ДИФФЕРЕНЦИРОВАНИЯ
Wy ( ) Wx ( )
2
Условие дифференцируемости
случайного процесса:
1
Ry (0)
2
W
(
)
d
x
2

12.

ФУНКЦИЯ ВЗАИМНОЙ КОРРЕЛЯЦИИ
ВХОДНОГО И ВЫХОДНОГО ПРОЦЕССОВ
dx(t ) d
Rxy ( ) x(t )
x(t ) x(t )
d
d
Rxy ( ) Rx ( )
Некоррелированность входного и
выходного процессов:
Rxy (0) Rx (0) 0

13.

ИНТЕГРИРОВАНИЕ СЛУЧАЙНЫХ
ПРОЦЕССОВ
t
y (t ) x( )d
0
Математическое ожидание:
t
mx 0, m y x( )d mxt
0
Выходной процесс при не центрированном
стационарном процессе на входе не является
стационарным

14.

ФУНКЦИЯ КОРРЕЛЯЦИИ РЕЗУЛЬТАТА
ИНТЕГРИРОВАНИЯ
t1
t2
0
0
mx 0, R y (t1 , t 2 ) x( )d x( )d
t 2 t1
t 2 t1
0 0
0 0
x( ) x( )d d Rx ( )d d
Выходной процесс при центрированном
стационарном процессе на входе не является
стационарным

15.

ИСТОЧНИКИ ШУМОВ В
РАДИОТЕХНИЧЕКИХ ЦЕПЯХ
1. ТЕПЛОВОЙ ШУМ
R
N
0
un(t)
N0=4kTR
f

16.

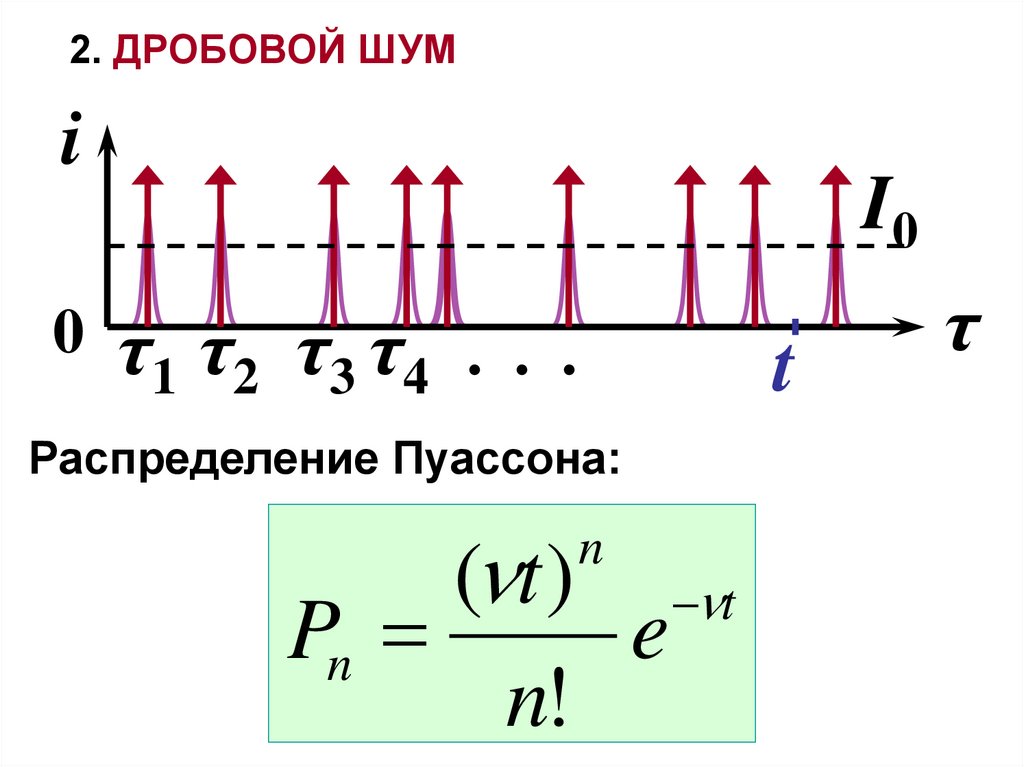
2. ДРОБОВОЙ ШУМ
i
0
I0
τ1 τ2 τ3 τ4 . . .
t
Распределение Пуассона:
( t ) t
Pn
e
n!
n
τ

17.

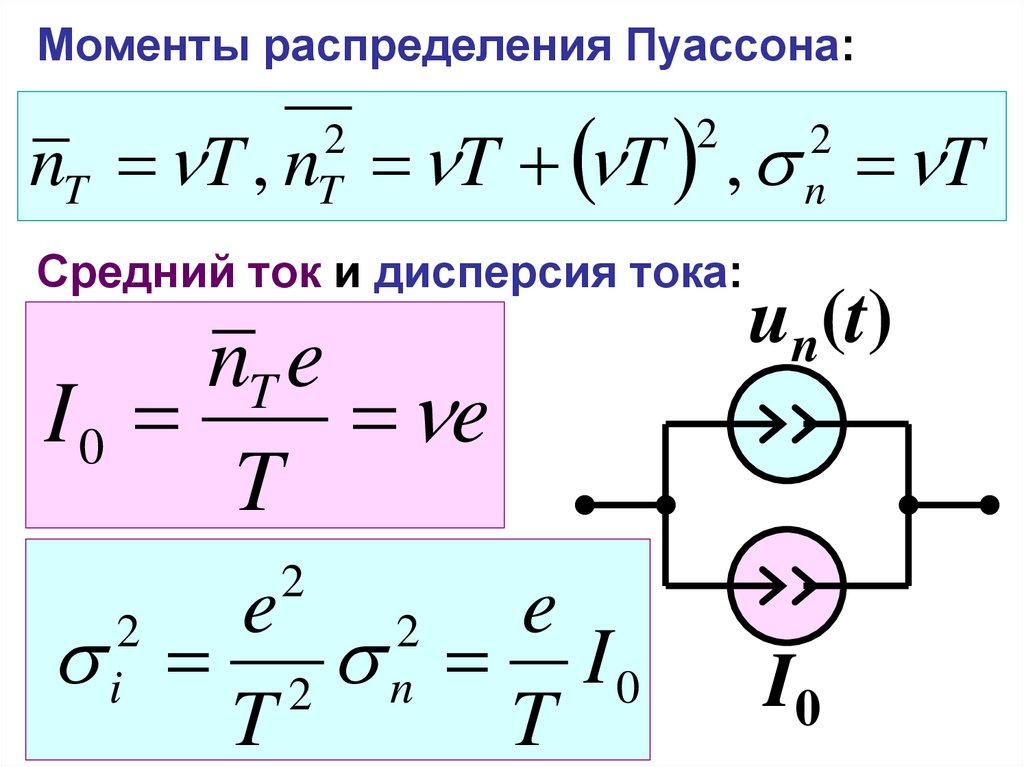
Моменты распределения Пуассона:
nT T , n T T , T
2
T
2
Средний ток и дисперсия тока:
nT e
I0
e
T
2
n
un(t)
2
e 2 e
2 n I0
T
T
2
i
I0

18.

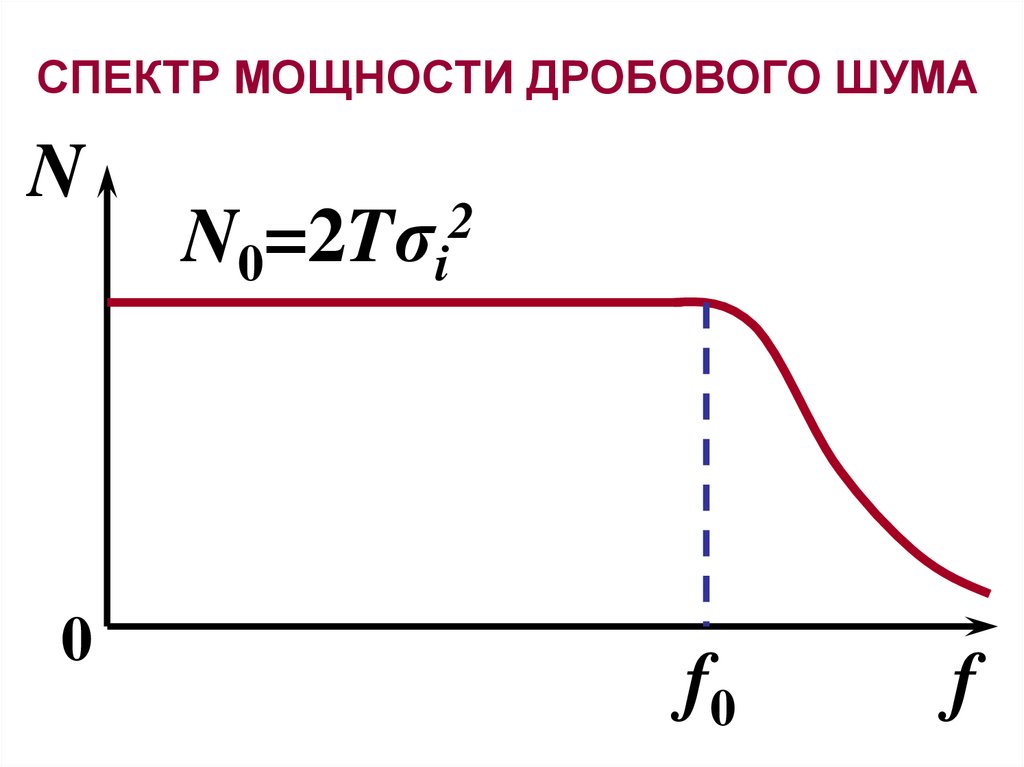
СПЕКТР МОЩНОСТИ ДРОБОВОГО ШУМА
N
0
2
N0=2Tσi
f0
f

19.

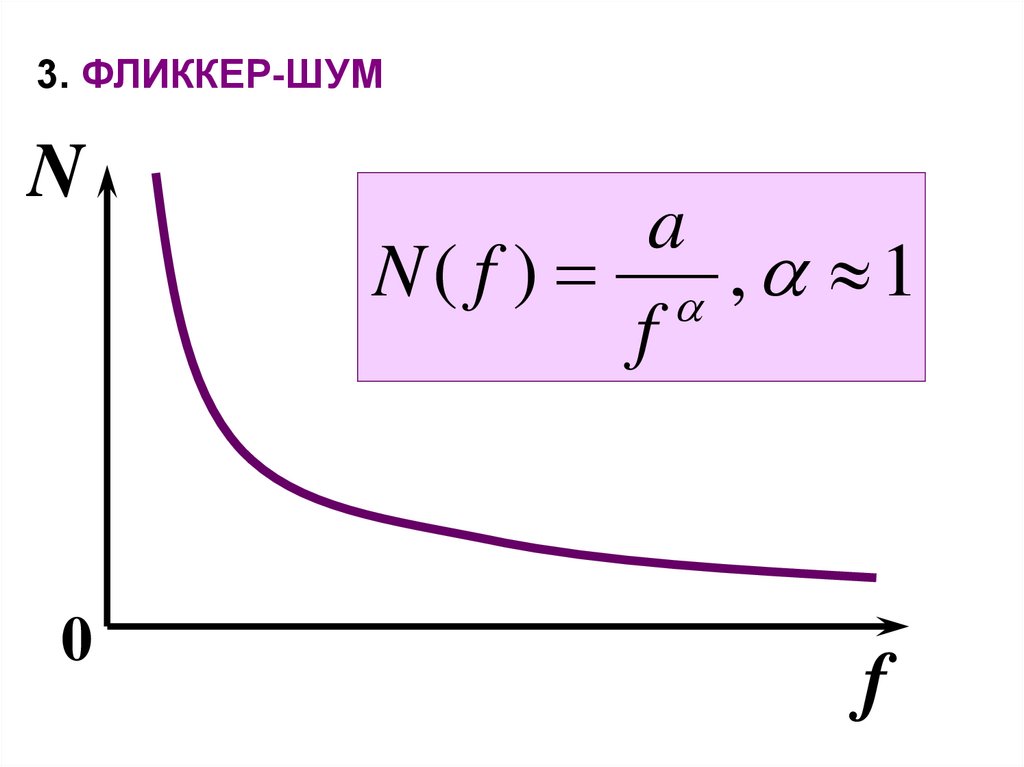
3. ФЛИККЕР-ШУМ
N
0
a
N( f ) , 1
f
f

20.

СЛУЧАЙНЫЕ ПРОЦЕССЫ В ЛИНЕЙНЫХ
НЕСТАЦИОНАРНЫХ ЦЕПЯХ
x(t)
h(t,τ)
y(t)
Реализация выходного процесса:
(t )
y(t )
h
(
t
,
)
x
(
)
d

21.

ФУНКЦИЯ КОВАРИАЦИИ ВЫХОДНОГО ПРОЦЕССА
By (t1 , t 2 ) y (t1 ) y (t 2 )
h
(
t
,
)
x
(
)
d
h
(
t
,
)
x
(
)
d
1
1
1
1
2
2
2
2
h
(
t
,
)
h
(
t
,
)
x
(
)
x
(
)
d
d
1
1
2
2
1
2
1
2

22.

Функция ковариации выходного процесса
при независимых x(t) и h(t, τ)
By (t1 , t 2 )
K
(
t
,
t
,
,
)
B
(
,
)
d
d
1
2
1
2
x
1
2
1
2
Ковариационная характеристика цепи
K (t1 , t2 , 1 , 2 ) h(t1 , 1 )h(t2 , 2 )
Функция ковариации входного процесса
Bx ( 1 , 2 ) x( 1 ) x( 2 )

23.

Безынерционная нестационарная цепь
y(t0 ) L[ x(t0 )], h(t , ) k (t ) (t )
By (t1 , t 2 ) k (t1 ) (t1 1 ) x( 1 )d 1
k (t2 ) (t2 2 ) x ( 2 )d 2 K (t1 , t 2 ) Bx (t1 , t 2 )
K (t1 , t 2 ) k (t1 )k (t 2 )
Ковариационная
характеристика
безынерционной цепи

24.

Функция ковариации выходного
процесса безынерционной
нестационарной цепи равна
произведению ковариационной
характеристики цепи и
функции ковариации входного процесса
при условии, что данная функция и
импульсная характеристика цепи
являются статистически независимыми

25.

Прохождение гармонического сигнала
x(t ) cos 0t
через безынерционную цепь с
флуктуирующим коэффициентом
передачи
K (t , j ) k0 k (t )
Функция ковариации постоянной
составляющей k0
B0 ( ) k 2 k ( )
2
0
2
0

26.

Функция ковариации флуктуационной
составляющей Δk(t)
c a
2c
B ( ) e
2
2
a
a
Спектр мощности коэффициента
передачи
2c
WK ( ) 2 k ( ) 2
2
a
2
0

27.

Ковариационная характеристика цепи
c a
K ( ) F WK ( ) k e
a
1
2
0
Функции ковариации входного и
выходного процессов
1
Bx ( ) cos 0
2
1 2 c a
By ( ) K ( ) Bx ( ) k 0 e
2
a
cos 0

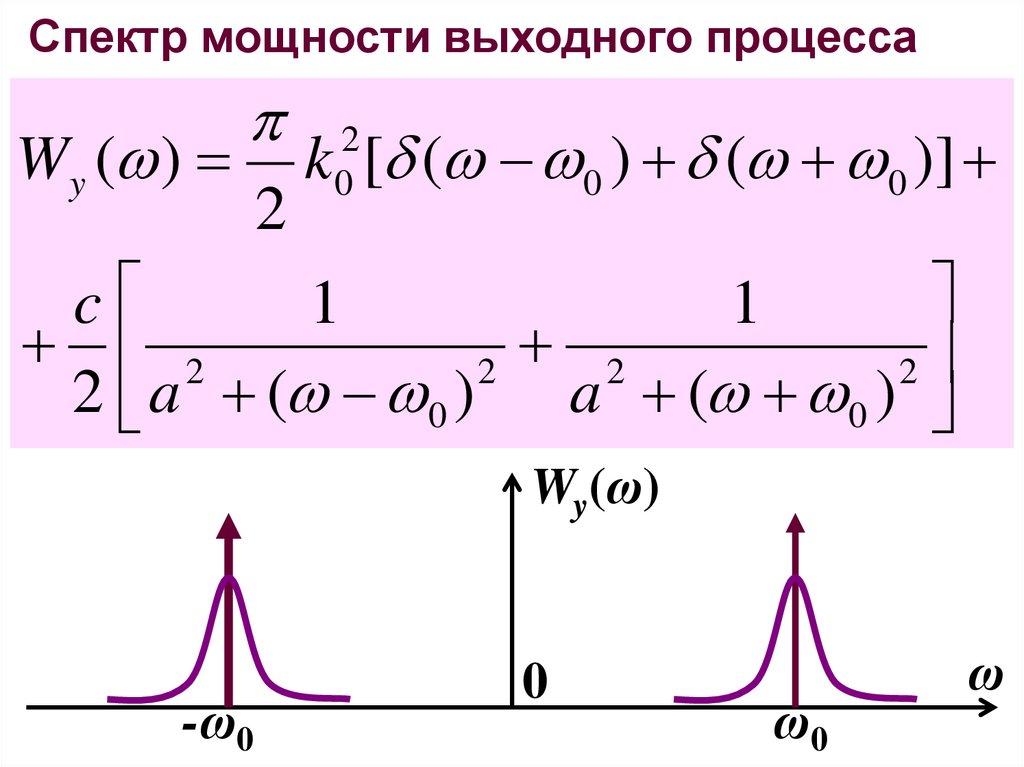
28.

Спектр мощности выходного процесса
Wy ( )
2
k [ ( 0 ) ( 0 )]
2
0
c
1
1
2
2
2
2
2 a ( 0 )
a ( 0 )
Wy(ω)
-ω0
0
ω0
ω

29.

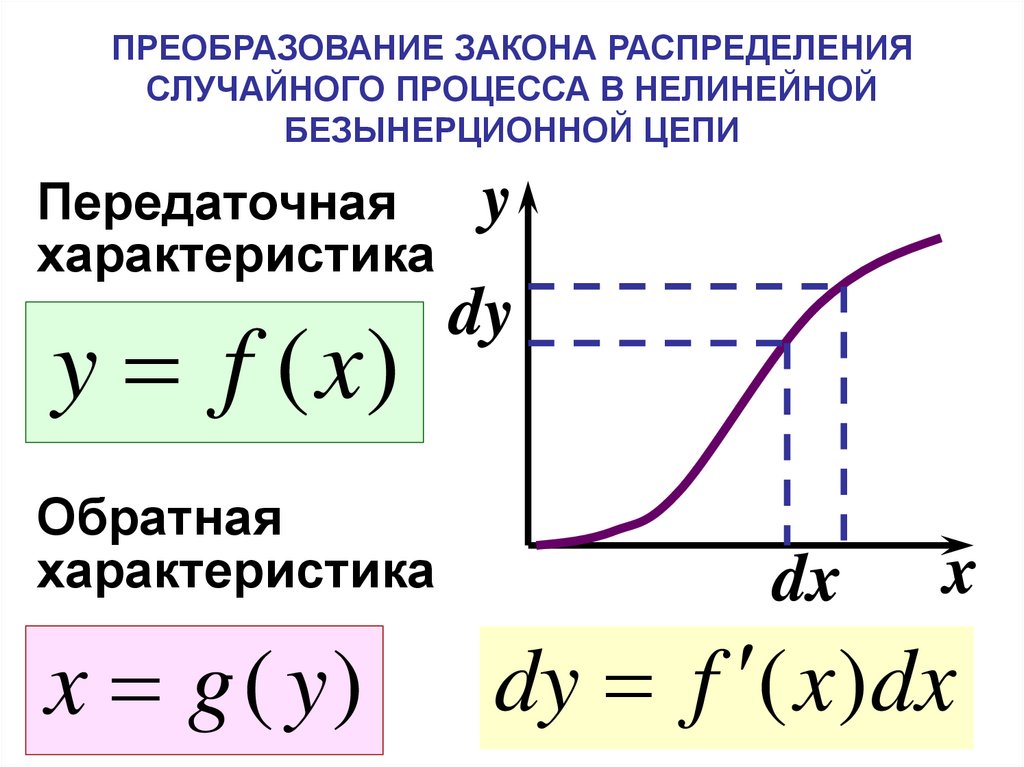
ПРЕОБРАЗОВАНИЕ ЗАКОНА РАСПРЕДЕЛЕНИЯ
СЛУЧАЙНОГО ПРОЦЕССА В НЕЛИНЕЙНОЙ
БЕЗЫНЕРЦИОННОЙ ЦЕПИ
Передаточная
характеристика
y
y f (x)
dy
Обратная
характеристика
x g ( y)
dx
x
dy f ( x)dx

30.

ПРЕОБРАЗОВАНИЕ ЗАКОНА РАСПРЕДЕЛЕНИЯ
СЛУЧАЙНОГО ПРОЦЕССА В НЕЛИНЕЙНОЙ
БЕЗЫНЕРЦИОННОЙ ЦЕПИ
Вероятности нахождения случайных
процессов x(t) и y(t) на интервалах
шириной dx и dy :
px ( x) dx py ( y) dy
dx
p y ( y ) px ( x)
dy

31.

ПРЕОБРАЗОВАНИЕ ЗАКОНА РАСПРЕДЕЛЕНИЯ
СЛУЧАЙНОГО ПРОЦЕССА В НЕЛИНЕЙНОЙ
БЕЗЫНЕРЦИОННОЙ ЦЕПИ
Плотность вероятности выходного
случайного процесса y(t)
dg ( y)
p y ( y) px g ( y)
dy

32.

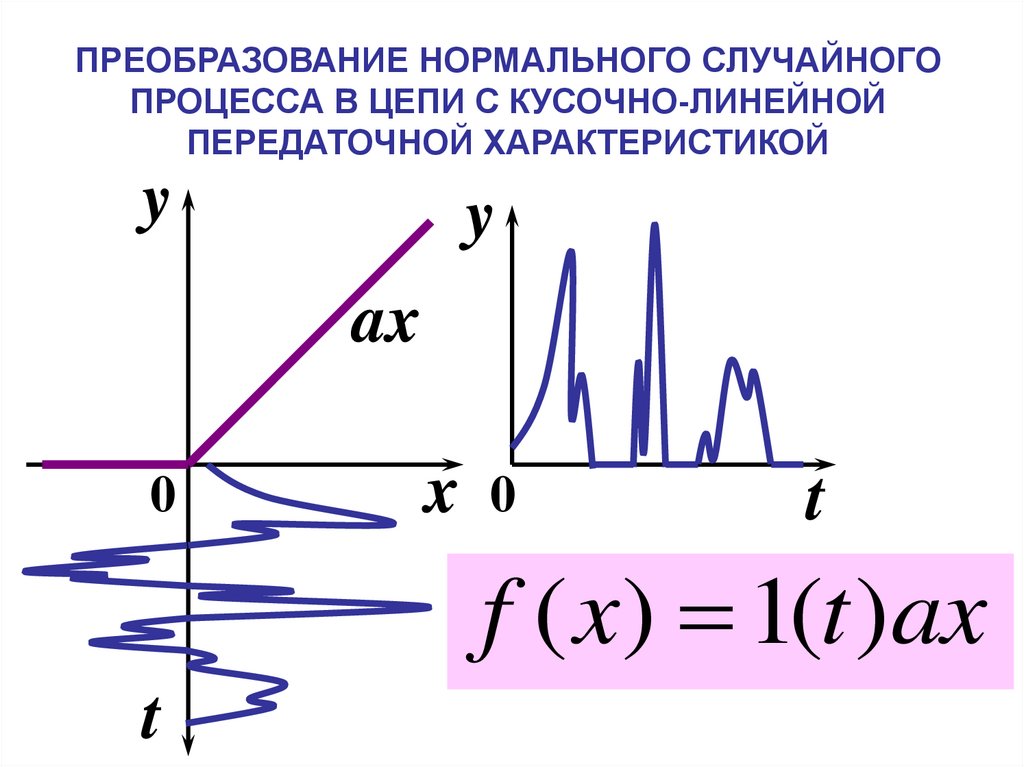
ПРЕОБРАЗОВАНИЕ НОРМАЛЬНОГО СЛУЧАЙНОГО
ПРОЦЕССА В ЦЕПИ С КУСОЧНО-ЛИНЕЙНОЙ
ПЕРЕДАТОЧНОЙ ХАРАКТЕРИСТИКОЙ
y
y
ax
0
x
0
t
f ( x) 1(t )ax
t

33.

ПЛОТНОСТЬ ВЕРОЯТНОСТИ ВХОДНОГО
СТАЦИОНАРНОГО ПРОЦЕССА
1
p ( x)
e
2 x
x
2
2
2 x
dy
dx , y 0
a1( x ), 1
dx
dy a , y 0

34.

ПЛОТНОСТЬ ВЕРОЯТНОСТИ ВЫХОДНОГО
ПРОЦЕССА
, y 0
2
y
2 2
p( y )
1
2a x
e
,
y
0
a 2
x

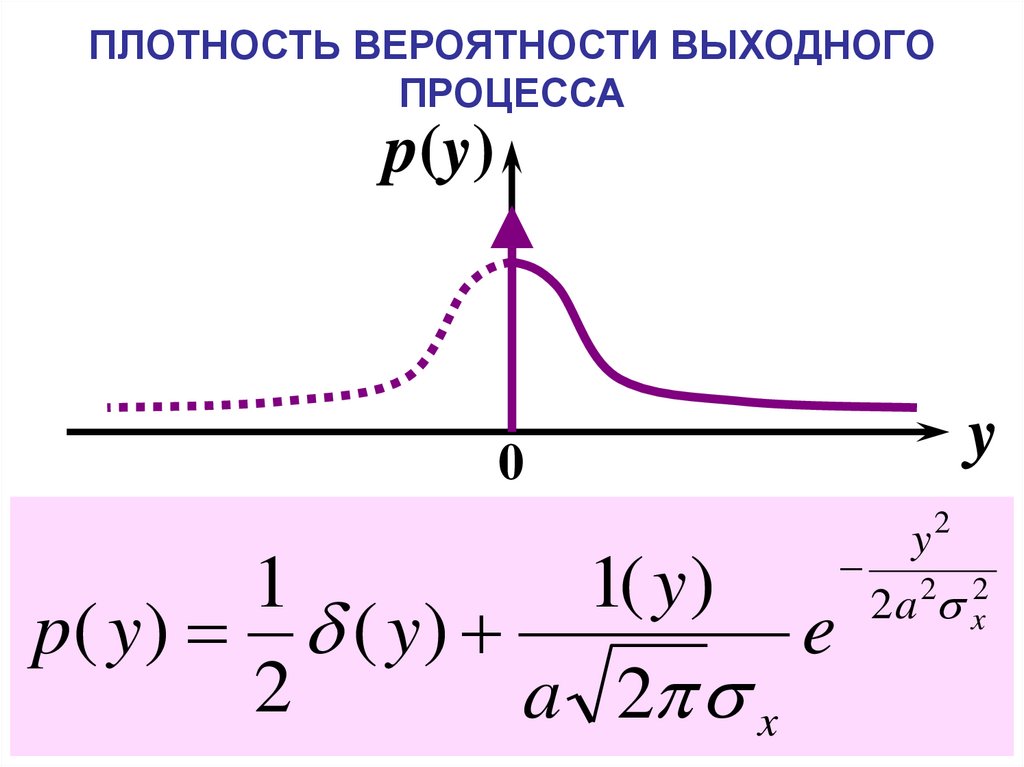
35.

ПЛОТНОСТЬ ВЕРОЯТНОСТИ ВЫХОДНОГО
ПРОЦЕССА
p(y)
y
0
1
1( y )
p( y ) ( y )
e
2
a 2 x
y
2
2 a 2 x2

36.

ФУНКЦИЯ КОВАРИАЦИИ ВЫХОДНОГО ПРОЦЕССА
БЕЗЫНЕРЦИОННОЙ ЦЕПИ
By (t1 , t 2 ) y(t1 ) y(t2 ) { f [ x(t1 )] f [ x(t2 )]
Двумерная плотность вероятности
нормального стационарного
узкополосного входного процесса
p( x1 , x2 , )
1
2
2
x
1 r ( )
2
e
x12 x22 2 r ( ) x1 x2
2 x2 [1 r 2 ( )]

37.

Симметричная квадратичная
передаточная характеристика цепи:
f ( x) bx
2
Функция корреляции входного
узкополосного процесса с
симметричным спектром мощности
Rx ( ) a( ) cos 0

38.

ФУНКЦИЯ КОВАРИАЦИИ ВЫХОДНОГО
ПРОЦЕССА НЕЛИНЕЙНОЙ БЕЗЫНЕРЦИОННОЙ
ЦЕПИ
By ( )
f ( x1 ) f ( x2 ) p( x1 , x2 , )dx1dx2
b 2b R ( )
2
4
x
2
2
x
By ( ) b b a ( )
2
4
x
2
4
x
b a ( ) cos 2 0
2
4
x
2
2

39.

СПЕКТР МОЩНОСТИ ВЫХОДНОГО ПРОЦЕССА
W ( ) W0 ( ) Wlf ( ) Whf ( )
Составляющая спектра мощности,
обусловленная постоянной
составляющей на выходе цепи с
квадратичной передаточной
характеристикой:
W0 ( ) b 2 ( )
2
4
x

40.

СПЕКТР МОЩНОСТИ ВЫХОДНОГО ПРОЦЕССА
Составляющая спектра мощности,
обусловленная низкочастотной
флуктуационной составляющей, спектр
мощности которой примыкает к нулевой
частоте:
Wlf ( ) b
2
2
4
x
a
(
)
e
4
2
2
j
d

41.

СПЕКТР МОЩНОСТИ ВЫХОДНОГО ПРОЦЕССА
Составляющая спектра мощности,
обусловленная высокочастотной
флуктуационной составляющей, со
спектром мощности,
сосредоточенным в
2 4
2
j
окрестности
W
a ( 2ω
)e 0: d
lf ( ) b частоты
x
Whf ( ) b
2
4
2
x
a
( ) cos(2 0 )e
j
d

42.

ОДНОСТОРОННИЙ СПЕКТР МОЩНОСТИ ВЫХОДНОГО
ПРОЦЕССА
F(ω)
F0(ω)
Fhf(ω)
Flf(ω)
0
ω0
2ω0
ω