Синтез систем автоматического управления

1. СИНТЕЗ СИСТЕМ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ

1) Влияние обратных связей на динамические
свойства объекта
2) Применение регуляторов для улучшения
качества
работы
систем
автоматического
управления
3) Типовые законы регулирования линейных
систем
4)Расчет
параметров
регуляторов
непрерывного действия по критерию качества

2. 1) Влияние обратных связей на динамические свойства объекта

Основные виды корректирующих обратных связей следующие:
•жесткая обратная связь
•инерционная жесткая обратная связь
•гибкая обратная связь
•инерционная гибкая обратная связь

3.

– Охват апериодического звена жесткой отрицательной обратной
связью
Общая передаточная функция будет

4.

Следовательно, отрицательная жесткая обратная связь уменьшает
инерционность звена. Тем самым она улучшает качество переходного
процесса в системе и может оказывать стабилизирующее действие, т.е.
превращать неустойчивую замкнутую систему в устойчивую. Это означает
увеличение быстродействия системы, но и потерю мощности сигнала на
выходе.

5.

6.

При охвате интегрирующего звена отрицательной жесткой
обратной связью
получаем
Под действием жесткой обратной связи теряется интегрирующее
свойство звена, и оно превращается в апериодическое с
коэффициентом усиления, который целиком определяется только
обратной связью.

7.

8.

– Охват апериодического звена гибкой отрицательной обратной
связью
где k*=k – прежний коэффициент усиления,
Т*=Т+kkoc – увеличивается.
Охват апериодического звена гибкой отрицательной связью не изменяет
коэффициент усиления системы и увеличивает постоянную времени, что
приводит к увеличению времени регулирования системы без потерь
мощности выходного сигнала.
Дифференциальные звенья очень чувствительны к помехам, поэтому к
системам с гибкими отрицательными связями для уменьшения помех
дополнительно ставятся фильтры.

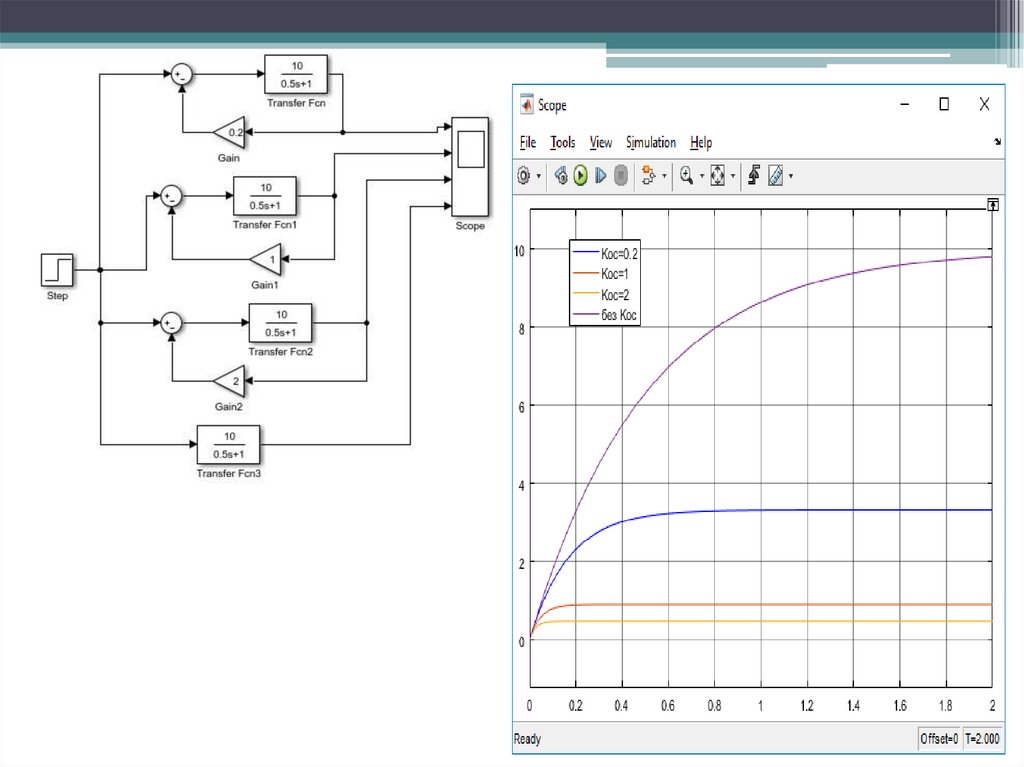
9.

w1 =
10
--------0.2 s + 1
w2 =
0.1 s
>> wz=feedback(w1,w2)
wz =
10
--------1.2 s + 1
w1 =
10
--------0.2 s + 1
w2 =
0.5 s
>> wz=feedback(w1,w2)
wz =
10
--------5.2 s + 1

10.

– Охват апериодического звена гибкой положительной обратной
связью
где k*=k – прежний коэффициент усиления,
Т*=Т-kkoc – уменьшается.
Гибкая положительная обратная связь уменьшает время переходного
процесса, не уменьшая мощность выходного сигнала.
Поэтому, если объект представляет собой колебательную систему с
большими начальными амплитудами, то гибкая положительная обратная
связь будет уменьшать колебательность системы.

11.

Т*=Т-kkoc>0 koc<T/k условие устойчивости
w1 =
10
--------0.2 s + 1
w2 =
0.01 s
>> wz=feedback(w1,w2,1)
wz =
10
--------0.1 s + 1
w1 =
10
--------0.2 s + 1
w2 =
0.015 s
>> wz=feedback(w1,w2,1)
wz =
10
--------0.05 s + 1

12. 2) Применение регуляторов для улучшения качества работы систем автоматического управления

2) Применение регуляторов
качества
работы
систем
управления
для улучшения
автоматического
Одним из наиболее распространенных способов обеспечения требуемых
показателей качества (устойчивость, точность, быстродействие) является
использование регуляторов. Наибольшее распространение в промышленности
получили релейные регуляторы и стабилизирующие регуляторы.
Стабилизирующие (типовые) регуляторы являются наиболее
универсальными и распространенными регуляторами. В силу своей
универсальности они легко приспосабливаются для автоматизации
разнообразных технологических процессов и объектов.
Типовые регуляторы реализуют типовые законы управления.
Закон управления – это алгоритм или функциональная
зависимость, в соответствии с которыми регулятор формирует
управляющее воздействие u(t).

13.

Эта зависимость может быть представлена в виде:
u(t) = F(e, g, f)
где F – некоторый оператор от сигнала рассогласования e(t),
задающего воздействия v(t) и возмущающего воздействия f(t), а
также от их производных и интегралов по времени.
Обычно закон управления можно разделить по виду входного
сигнала на три слагаемых:
u(t) = F1(e) + F2(v) + F3(f),
где F1(e), F2(v) и F3(f)
выражают управление по отклонению,
задающему и внешнему воздействиям, соответственно.

14.

В зависимости от вида оператора F законы управления делятся
на стандартные и специальные:
• стандартные законы управления - это универсальные
законы, с помощью которых можно решать задачи автоматизации
разнообразных технологических процессов и объектов.
• специальные
законы
управления
это
законы,
формируемые для решения конкретных задач.
Стандартный закон управления имеет следующий вид:

15.

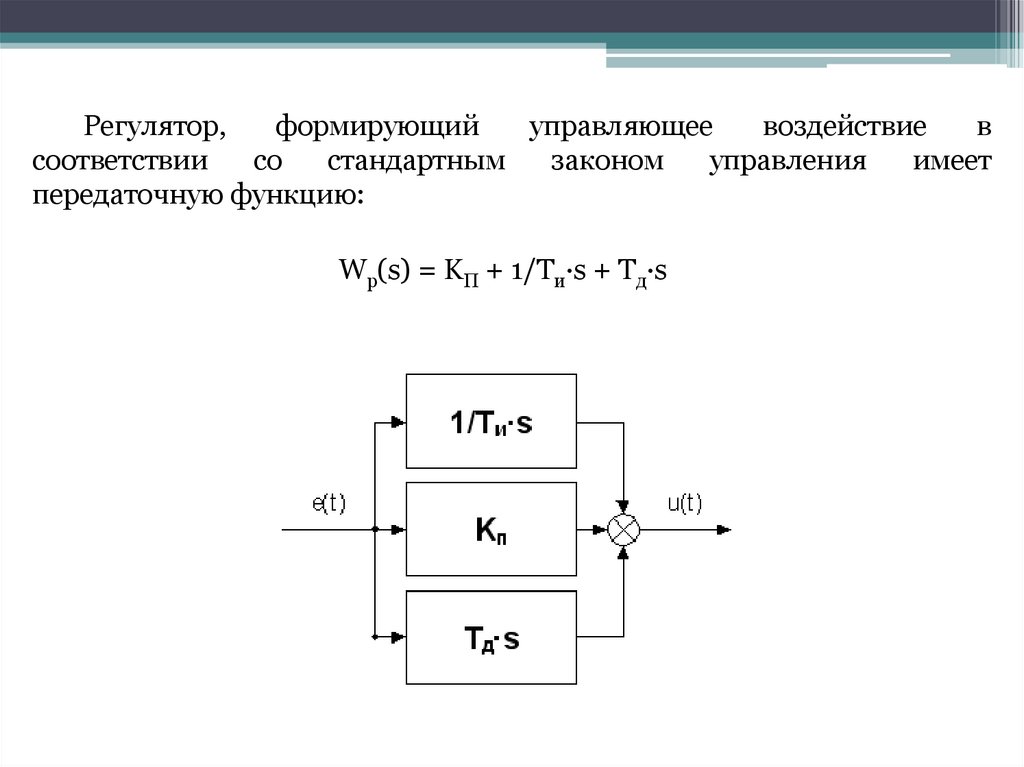
Регулятор,
формирующий
управляющее
воздействие
в
соответствии
со
стандартным
законом
управления
имеет
передаточную функцию:
Wр(s) = KП + 1/Tи·s + Tд·s

16.

Пропорциональная
составляющая
стандартного
управления позволяет уменьшить установившуюся ошибку:
закона
eуст = 1/(1 + Кп·Kо),
где Kо – коэффициент передачи объекта управления.
Интегральная составляющая вводится для повышения степени
астатизма системы и, следовательно для повышения точности: eуст = 0.
Дифференциальная составляющая непосредственно не влияет на
установившуюся ошибку. Однако она повышает запас устойчивости
системы, что позволяет компенсировать потерю устойчивости при
увеличении
вклада
пропорциональной
и
интегрирующей
составляющих.
Кроме того, дифференцирующая составляющая обеспечивает
повышение быстродействия и снижение динамической ошибки
системы, то есть работает с “предвидением” (предварением).

17. 3) Типовые законы регулирования линейных систем

П (пропорциональный) – регулятор:
Простейший
закон
регулирования
реализуется
безынерционного звена с передаточной функцией
при
помощи
Согласно этому выражению, управляющее воздействие и в статике
и в динамике пропорционально сигналу ошибки е. Поэтому такой
закон регулирования называется пропорциональным (П).
Преимуществами данного регулятора являются простота и
быстродействие, а недостатком – ограниченная точность.

18.

И (интегральный) – регулятор:
Закон регулирования, которому соответствует передаточная функция
При интегральном управлении получается астатическая система.
Повышение степени астатизма приводит к увеличению
установившейся точности системы, но одновременно снижает ее
быстродействие, а также приводит к ухудшению устойчивости.

19.

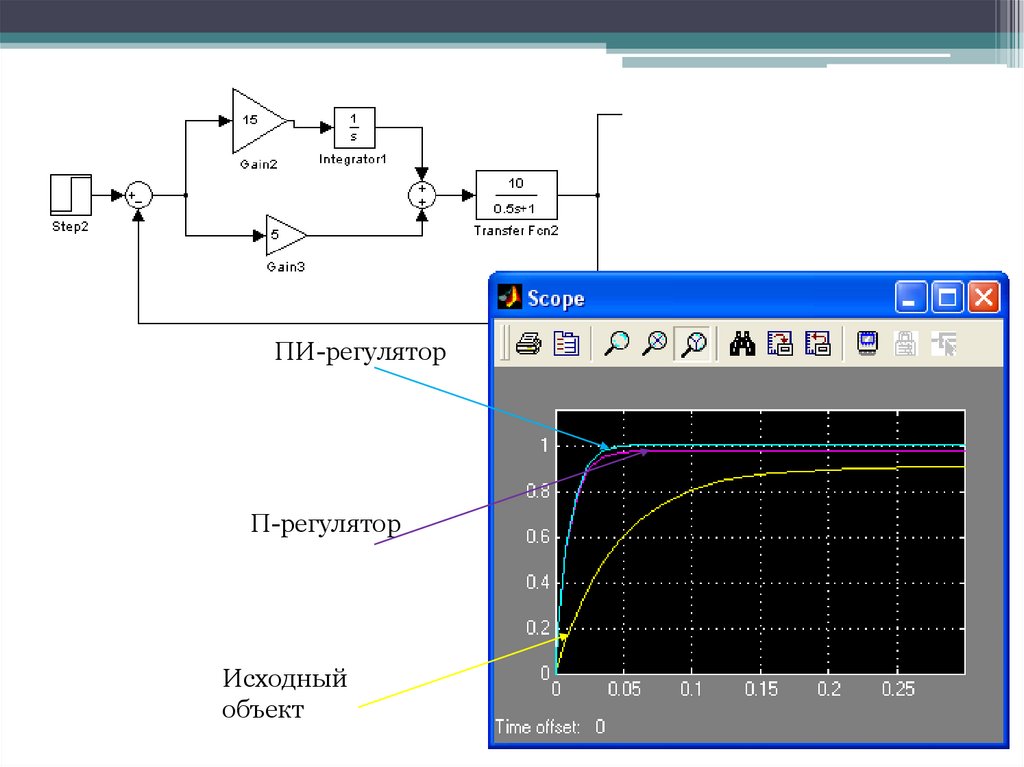
ПИ – регулятор:
Наибольшее распространение в промышленной автоматике
получил пропорционально-интегральный (ПИ) закон регулирования
Пропорционально-интегральное
(изодромное)
управление
сочетает в себе высокую точность интегрального управления
(астатизм)
с
большим
быстродействием
пропорционального
управления.
В первые моменты времени при появлении ошибки система с ПИрегулятором работает как система пропорционального регулирования,
а в дальнейшем начинает работать как система интегрального
управления.

20.

ПИ-регулятор
П-регулятор
Исходный
объект

21.

ПД – регулятор:
Наилучшее быстродействие достигается при пропорционально дифференциальном (ПД) законе регулирования
ПД – регулятор реагирует не только на величину сигнала ошибки, но и
на скорость его изменения. Благодаря этому при управлении достигается
эффект упреждения. Недостатком пропорционально – дифференциального
закона регулирования является ограниченная точность.
Пропорционально-дифференциальное управление применяются для
повышения быстродействия работы системы. В результате увеличивается
скорость реакции системы, повышается быстродействие, снижается ошибка
в динамике.

22.

23.

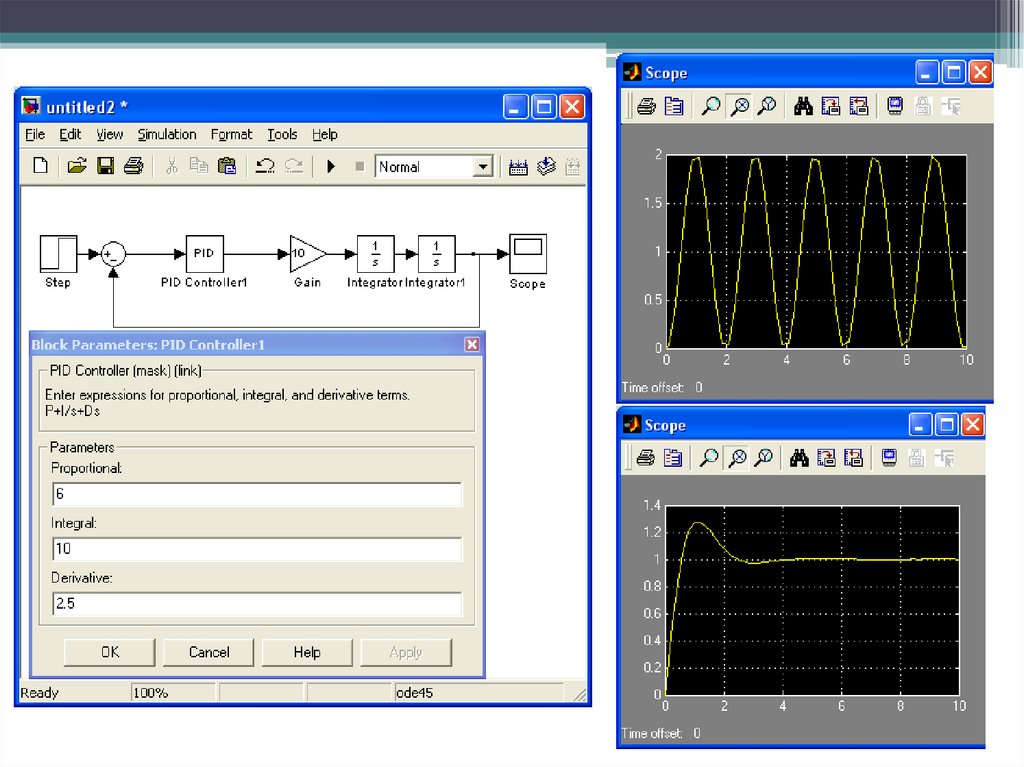
ПИД – регулятор:
Наиболее гибким законом регулирования (в классе линейных
законов) является пропорционально – интегрально –
дифференциальный (ПИД) закон
ПИД-регулятор, представляющий собой астатический изодромный
регулятор с предвидением, обеспечивает повышенную точность и
повышенное быстродействие системы.
Настройка такого регулятора заключается в задании значений
коэффициентов kp, Ti, Td таким образом, чтобы удовлетворить требованиям
качества управления в соответствии с выбранными критериями качества.

24.

Существует инженерный подход к синтезу ПИД–регуляторов–
методика Зиглера–Николса, которая предполагает следующие шаги:
1. Коэффициенты kd и ki устанавливаются равными нулю, а
коэффициент kp увеличивается до тех пор, пока система не потеряет
устойчивость.
2. Предельное значение kp обозначается как ku, а период
автоколебаний как pu
3. Значения коэффициентов ПИД – регулятора рассчитываются по
следующим формулам:

25.

26.

27.

28.

29.

Так как ПИД-регуляторы представляют собой систему второго
порядка, их можно успешно применять для управления процессами с
динамикой второго порядка.
ПИД – регуляторы можно успешно применять для большинства
технологических процессов, динамика которых имеет порядок выше
второго, так как они приближенно ведут себя подобно системам
второго порядка.

30. 4)Расчет параметров регуляторов непрерывного действия по критерию качества

Многие промышленные объекты управления одноконтурных
систем описываются передаточной функцией первого порядка с
запаздыванием
– коэффициент передачи в установившемся режиме;
– постоянная времени;
– запаздывание (задержка реакции объекта на единичное ступенчатое
воздействие).
Располагая значениями параметров объекта управления рассчитывают
параметры регулятора по формулам, приведенным в таблицах.
Таблицу выбирают на основании требований к форме ограничений на
время регулирования, величину перерегулирования, степень затухания
переходного процесса, чувствительность переходной функции к изменению
отношения

31.

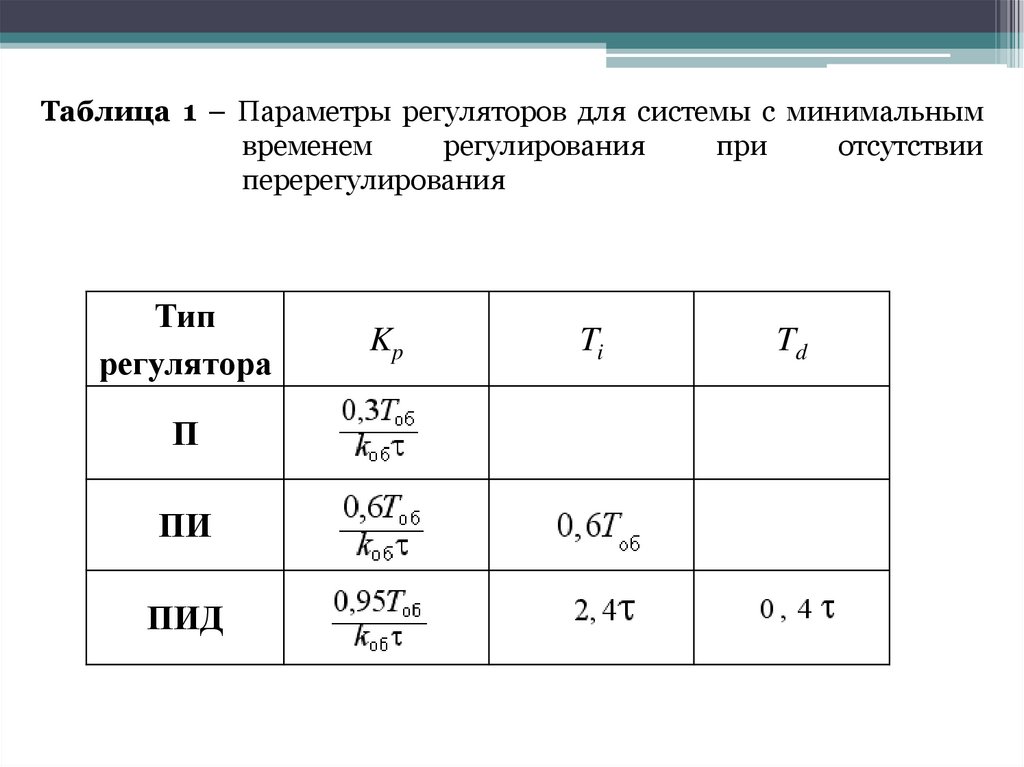
Таблица 1 – Параметры регуляторов для системы с минимальным
временем
регулирования
при
отсутствии
перерегулирования
Тип
регулятора
П
ПИ
ПИД
Kp
Ti
Td

32.

Таблица 2 – Параметры регуляторов для системы с минимальным
временем первого полупериода затухающих колебаний
при 20%-ном перерегулировании
Тип
регулятора
kp
Ti
Td
2
0, 4
П
ПИ
ПИД

33.

Таблица 3 – Параметры регуляторов по минимуму чувствительности
переходной функции системы к изменению отношения
при (10…20)%-ном перерегулировании
Тип
регулятора
П
ПИ
ПИД
kp
Ti
Td