Перпендикулярность прямой и плоскости

1.

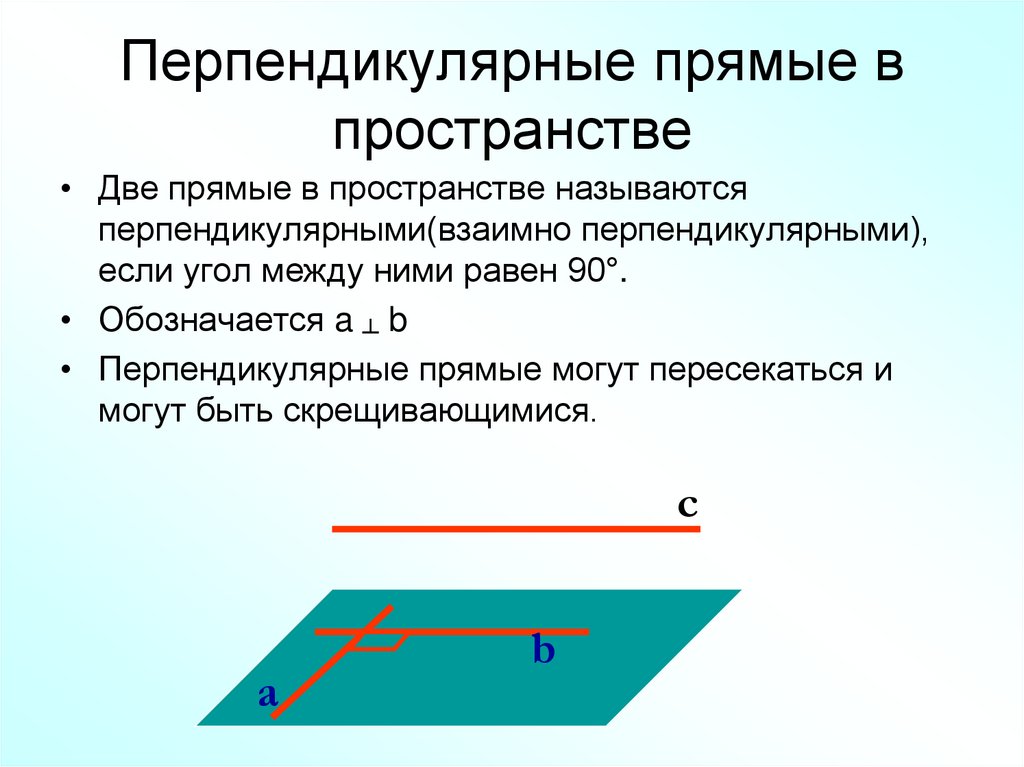
2. Перпендикулярные прямые в пространстве

• Две прямые в пространстве называются
перпендикулярными(взаимно перпендикулярными),
если угол между ними равен 90°.
• Обозначается a ┴ b
• Перпендикулярные прямые могут пересекаться и
могут быть скрещивающимися.
c
а
b

3. Лемма (о перпендикулярности двух параллельных прямых к третьей прямой)

• Если одна из двух параллельных
прямых перпендикулярна к третьей
прямой, то и другая прямая
перпендикулярна к этой прямой.

4. Лемма. Если одна из двух параллельных прямых перпендикулярна к третьей прямой, то и другая прямая перпендикулярна к этой

прямой.
а
b
c
M
C
A
Дано: а // b, а ┴ с.
Доказать: b ┴ с.
Доказательство:
Через произвольную точку
пространства М проведём:
МА и МС, параллельные
соответственно прямым а и с. Т.к. а
┴ с, то ĹАМС = 90°.
По условию а // b, по
построению а//МА => b//МА => b ┴ с.
Ч.т.д.

5. Параллельные прямые, перпендикулярные к плоскости

• Определение
Прямая называется перпендикулярной к
плоскости, если она перпендикулярна к
любой прямой, лежащей в этой плоскости.
Обозначается: а ┴ α
Говорят
также,
что
плоскость
перпендикулярна к прямой а

6.

Определение. Прямая называется перпендикулярной к
плоскости, если она перпендикулярна к любой прямой,
лежащей в этой плоскости.
a
a

7.

Канат в спортивном зале
перпендикулярен
плоскости пола.

8.

9. Примеры из окружающей обстановки

10.

11.

12.

13.

14.

15.

16.

17.

18.

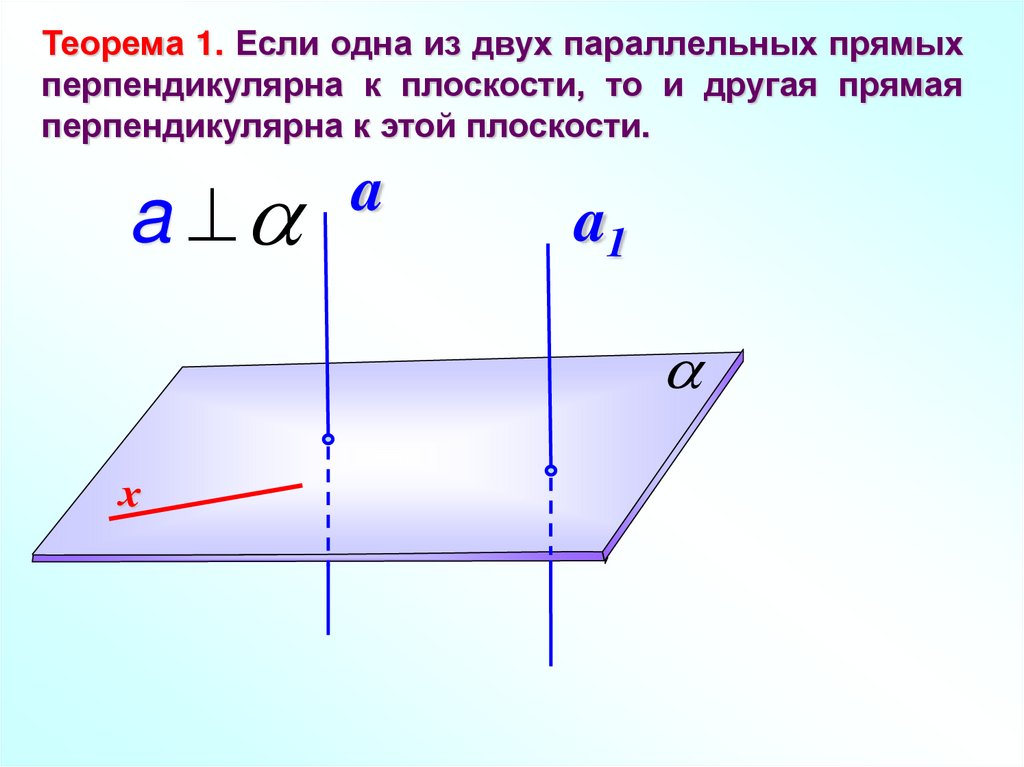
Теорема 1. Если одна из двух параллельных прямых
перпендикулярна к плоскости, то и другая прямая
перпендикулярна к этой плоскости.
a
a
a1

19.

Обратная теорема.
Если две прямые перпендикулярны к плоскости, то
они параллельны.
a
a
b
b
a II b

20.

Признак перпендикулярности прямой и плоскости.
Если прямая перпендикулярна к двум
пересекающимся прямым, лежащим в плоскости, то
она перпендикулярна к этой плоскости.
a
p
a p,
p
q
a q,
a

21.

Чтобы установить перпендикулярность
прямой и плоскости достаточно проверить
перпендикулярность лишь к двум прямым,
лежащим в плоскости.

22.

Теорема 2
Через любую точку пространства проходит
прямая, перпендикулярная к данной плоскости, и
притом только одна.
β
М
b
а
α
с
Дано: α; М α
Доказать:
1) ∃ с, с α, М с;
2) с – !
Доказательство:

23. Перпендикуляр и наклонные

М α
МН α
Н α
А α
В α
М
АН и ВН – проекции
наклонных
МН – перпендикуляр
α
Н
А
МА и МВ – наклонные
В

24. Теорема о трех перпендикулярах

Прямая, проведенная в плоскости через основание
наклонной перпендикулярно к ее проекции на эту
плоскость, перпендикулярна к самой наклонной.
А
α
Н
β
а
М
Дано: а α, АН α,
АМ – наклонная,
а НМ, М а
Доказать: а АМ
Доказательство:

25.

Теорема, обратная теореме о трех
перпендикулярах
Прямая, проведенная в плоскости через основание
наклонной перпендикулярно к ней, перпендикулярна
и к ее проекции.
А
α
Н
β
а
М
Дано: а α, АН α,
АМ – наклонная,
а АМ, М а
Доказать: а НМ
Доказательство: