Похожие презентации:
Формулы приведения. Единичная окружность. Готовимся к ЕГЭ
1.
Без труда не вытащишьи рыбку из пруда.
Готовимся к ЕГЭ
2. Готовимся к ЕГЭ «ФОРМУЛЫ ПРИВЕДЕНИЯ»
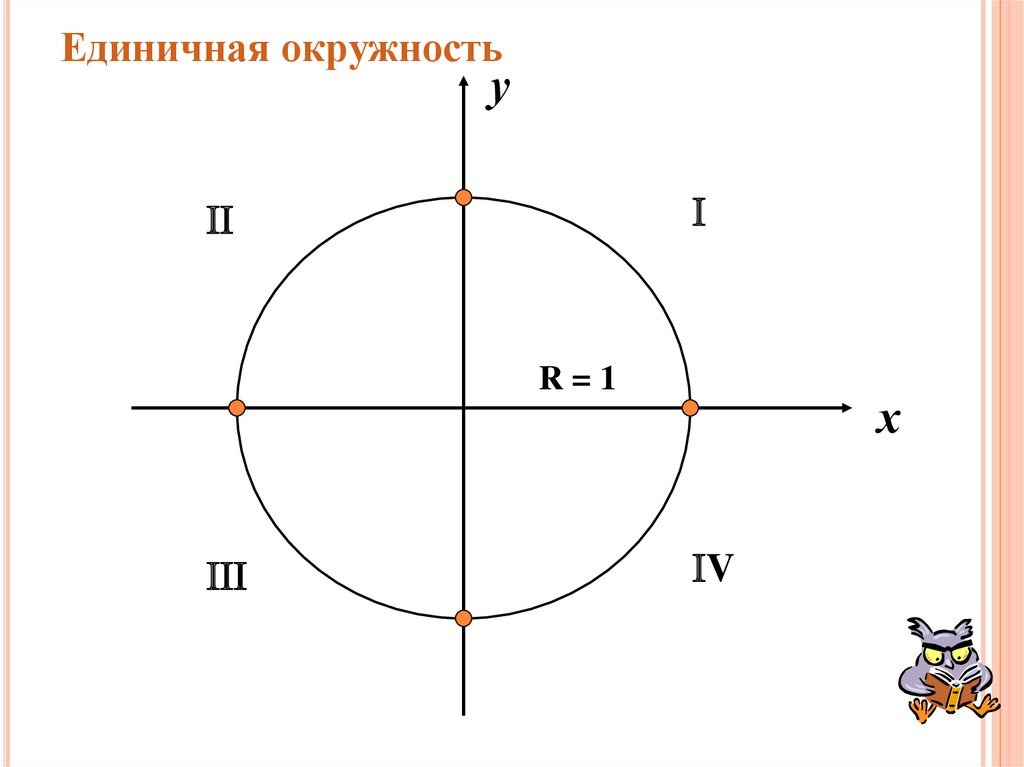
3. Единичная окружность
уR=1
х
V
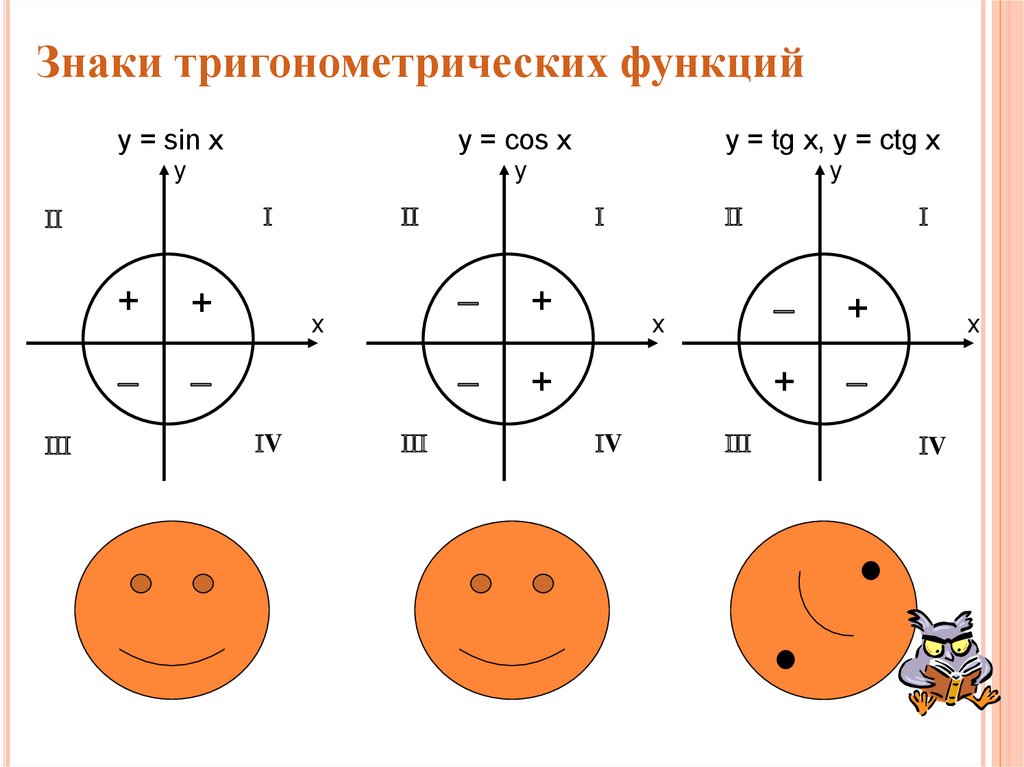
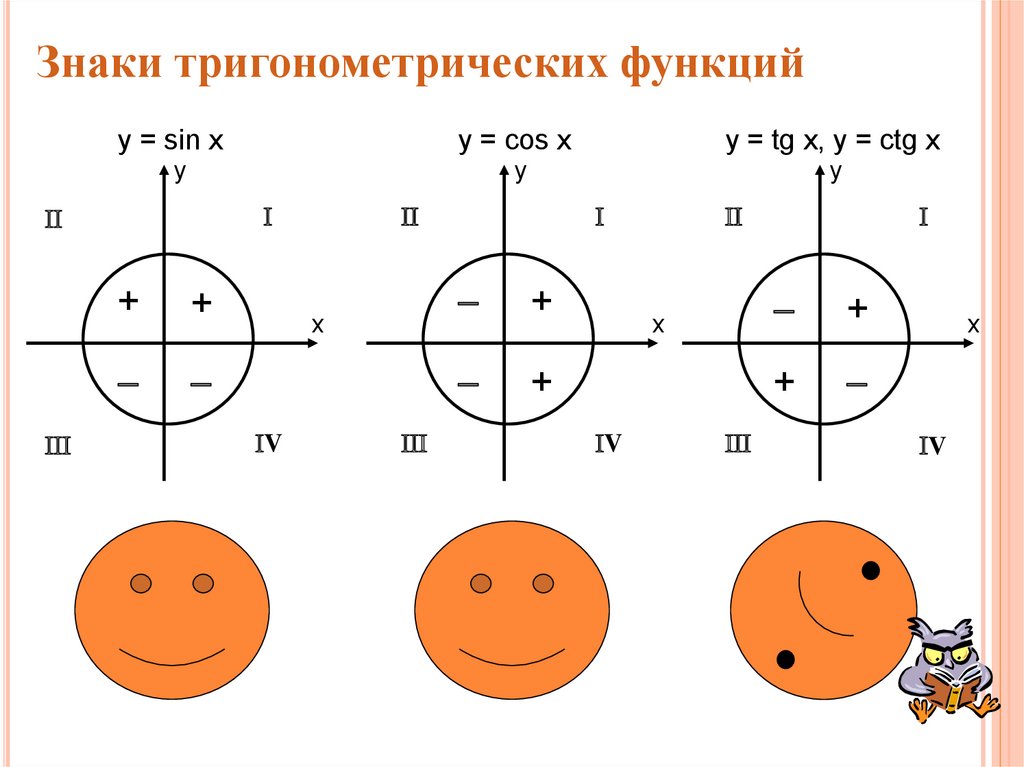
4. Знаки тригонометрических функций
y = sin xy = cos x
y = tg x, y = ctg x
y
y
y
+
+
x
V
+
+
x
V
+
+
x
V
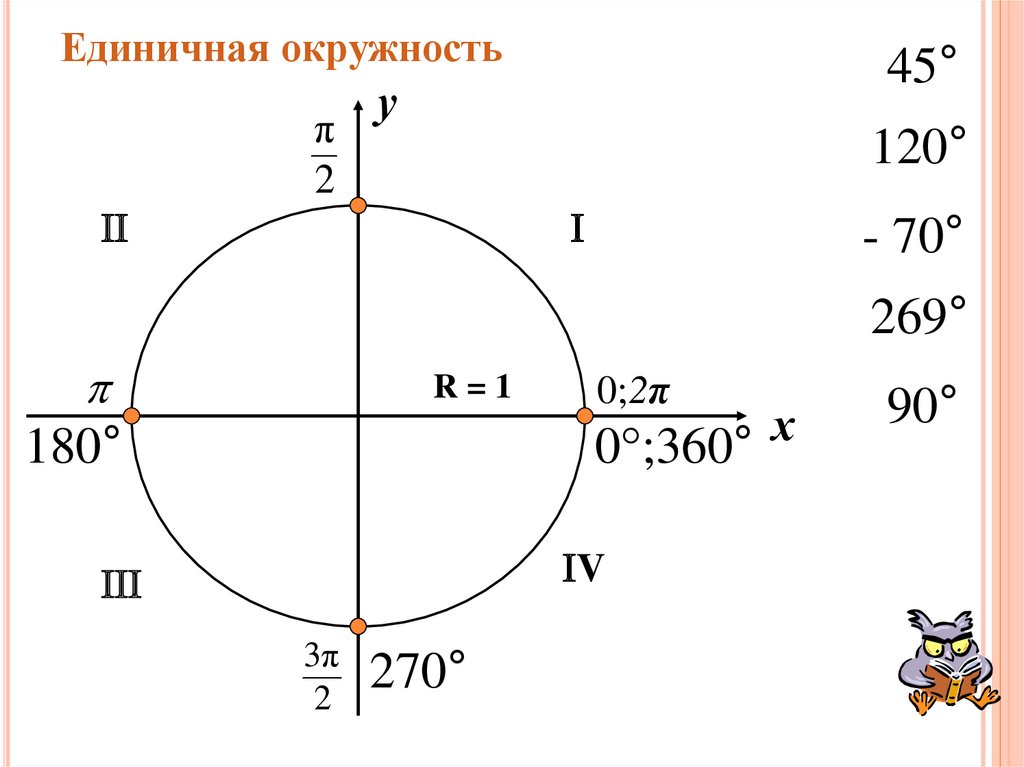
5. Единичная окружность
π2
45°
у
120°
- 70°
269°
R=1
180°
0;2π
х
0°;360°
V
3π
2
270°
90°
6.
1cos 60° =
2
1
sin =
2
6
tg 45° = 1
3
ctg 3 = 3
cos 135° = ?
7. ФОРМУЛЫ ПРИВЕДЕНИЯ
- это формулы, позволяющие выражатьзначения тригонометрических функций
углов вида π α ; π ± α ; 3π α ; 2π ± α
2
2
через функции угла первой четверти,
т.е
0 90 .
8. ФОРМУЛЫ ПРИВЕДЕНИЯ
хπ+α π–α 2π+α 2π–α π
α
2
π
α
2
3π
3π
α 2 α
2
sinx
- sinα
sinα
sinα
- sinα
cosα
cosα
- cosα
- cosα
cosx
- cosα
- cosα
cosα
cosα
- sinα
sinα
sinα
- sinα
tgx
tgα
- tgα
tgα
- tgα
- ctgα
ctgα
- ctgα
ctgα
ctgx
ctgα
- ctgα
ctgα
- ctgα
- tgα
tgα
- tgα
tgα
9. Алгоритм применения формул приведения
1) Определить, какой координатной четвертипринадлежит угол;
2) Найти знак данной функции в этой четверти;
3) Определить, меняется данная функция на
«кофункцию» или нет:
sinα cosα
tgα ctgα
10.
ЗАДАНИЕ 1. Применить формулы приведенияV
sin 2π α
sinα
π
sin α
2
V
+
cosα
cos 2π α cosα
sin π α sinα
tg 180 tg
ctg 270 tg
tg 90 ctg
3π
cos α sin α
2
11. ЗАДАНИЕ 2. Упростить выражение
3 cos 3 cos 360 cos 90 sin 1803 cos 3 cos sin sin
2sinα
12. ЗАДАНИЕ 3. Найти значение выражения:
IIcos (90° + 45°)
- sin 45°
2
cos 135° =
=
=
2
cos(180° - 45°)
- cos 45 °
4
sin
3
III
π
3π π
sin
= sin
3
3 3
3
- sin 2
3
13. Задание 4 (В7). Упростить выражение
ЗАДАНИЕ 4 (В7). Упростить выражениеsin 150° · tg225° =
sin 180 30 tg(180 45 )
= sin30 tg45
1
1
= 0,5
= 1
2
2
14. Задание 4 (В7). Упростить выражение
ЗАДАНИЕ 4 (В7). Упростить выражениеsin 150° · tg225° =
sin 180 30 tg(180 45 ) sin 90 60 tg(270 - 45 )
1
1
sin30
tg45
1
=
= cos60 ctg45 1
2
2
1
=
= 0,5
2
1
=
= 0,5
2
15.
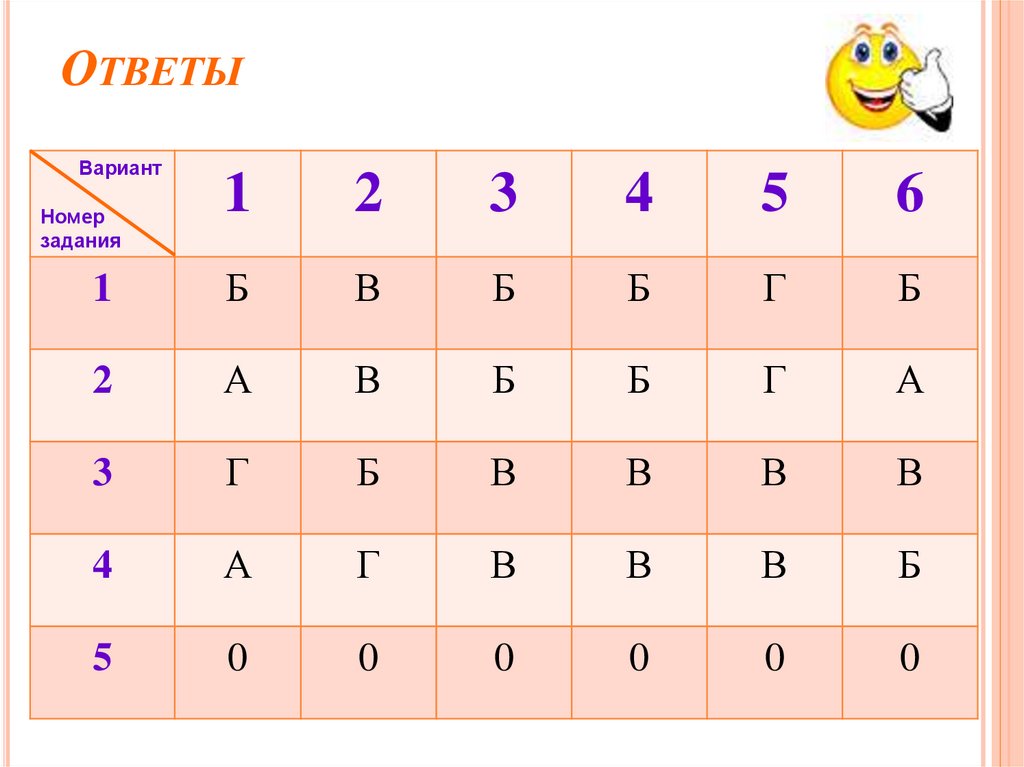
16. Ответы
ОТВЕТЫВариант
1
2
3
4
5
6
1
Б
В
Б
Б
Г
Б
2
А
В
Б
Б
Г
А
3
Г
Б
В
В
В
В
4
А
Г
В
В
В
Б
5
0
0
0
0
0
0
Номер
задания
17.
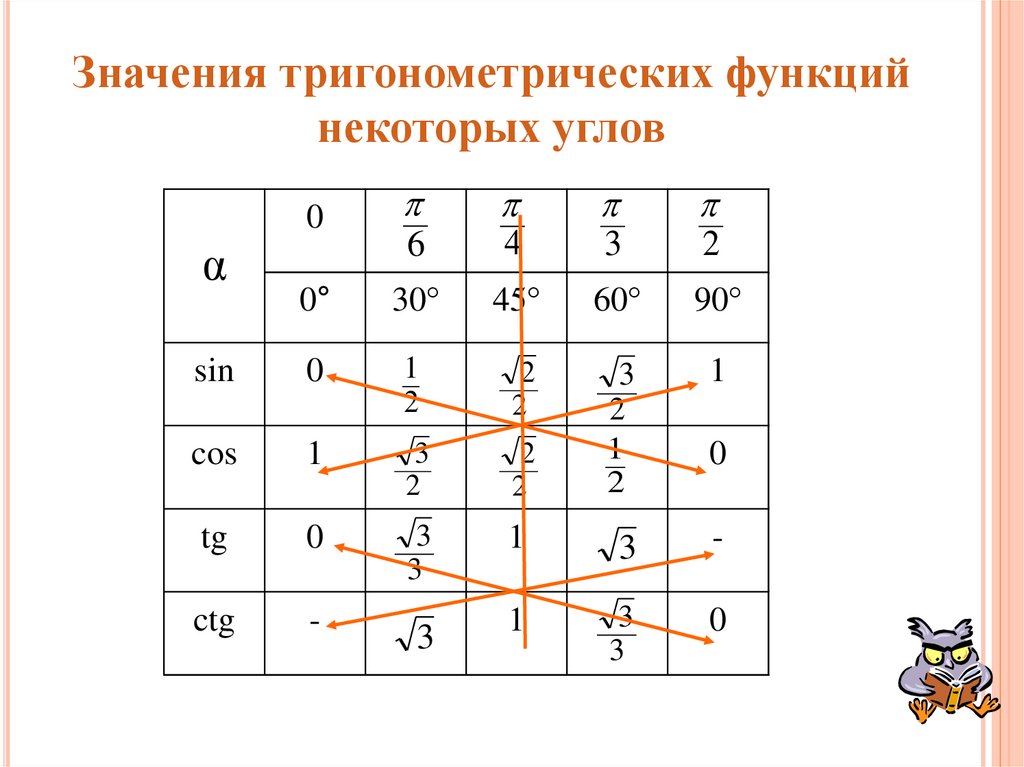
18. Значения тригонометрических функций некоторых углов
06
4
3
2
0°
30
45
60
90
sin
0
1
2
2
2
1
cos
1
3
2
2
2
3
2
1
2
tg
0
3
3
1
3
-
ctg
-
1
3
3
0
α
3
0
19. Знаки тригонометрических функций
y = sin xy = cos x
y = tg x, y = ctg x
y
y
y
+
+
x
V
+
+
x
V
+
+
x
V
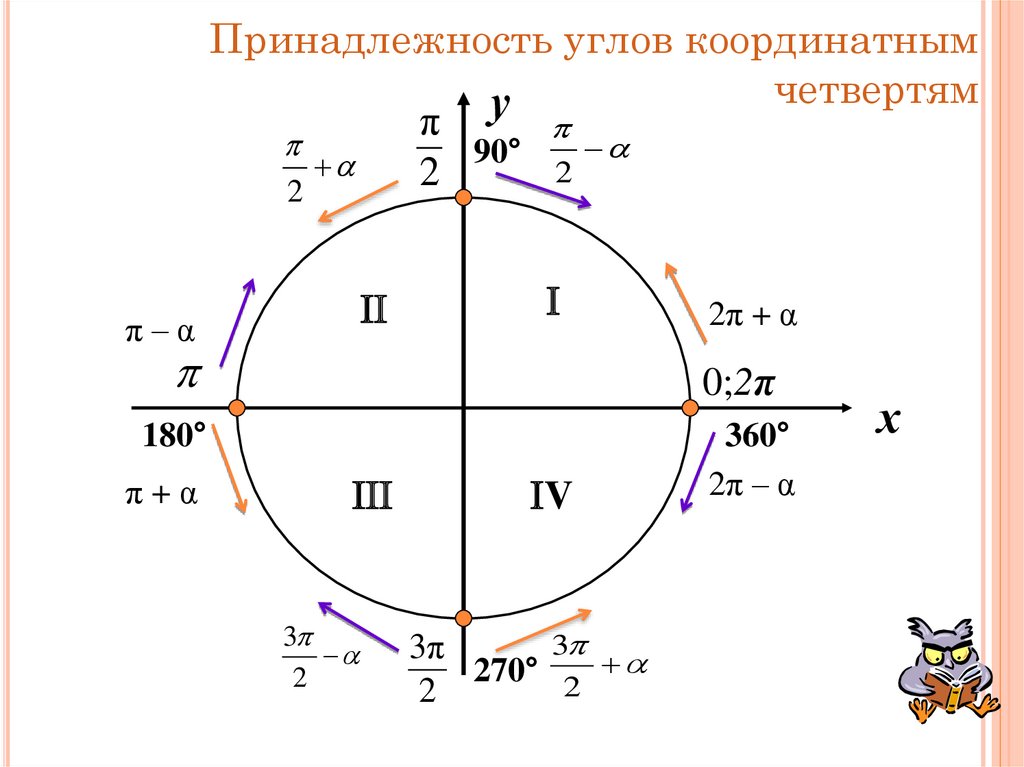
20. Принадлежность углов координатным четвертям
уπ
90°
2
2
2
π–α
0;2π
180°
π+α
2π + α
3
2
V
3
3π
270° 2
2
360°
2π – α
х
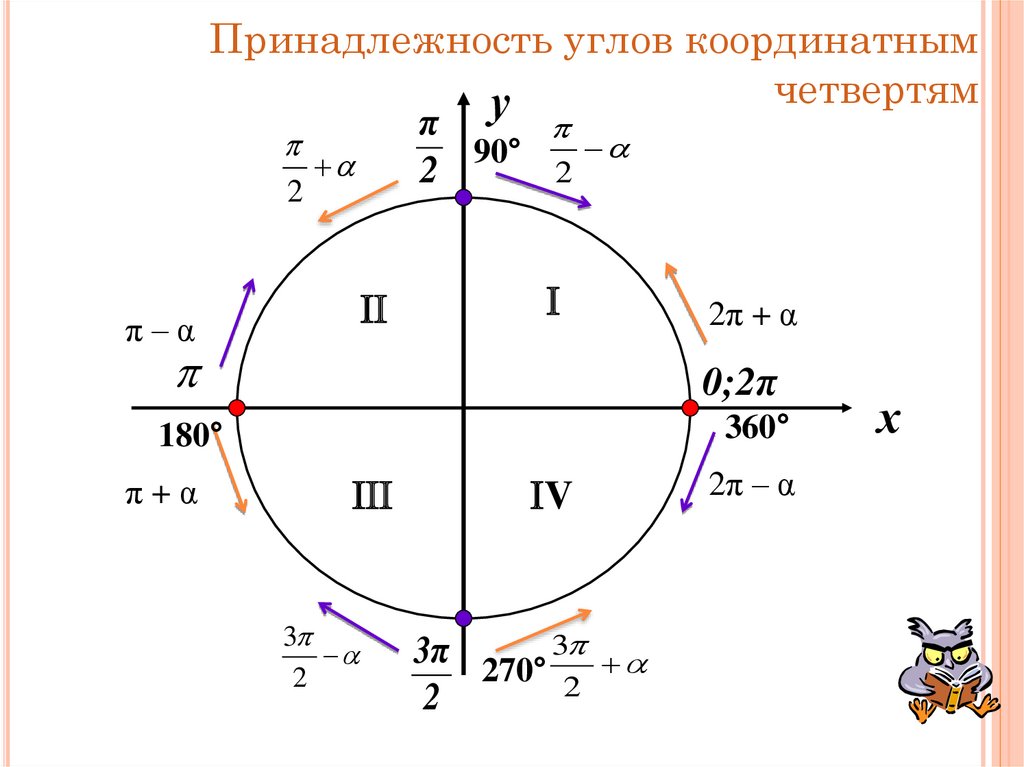
21. Принадлежность углов координатным четвертям
уπ
90°
2
2
2
π–α
0;2π
360°
180°
π+α
2π + α
3
2
V
3π 270° 3
2
2
2π – α
х


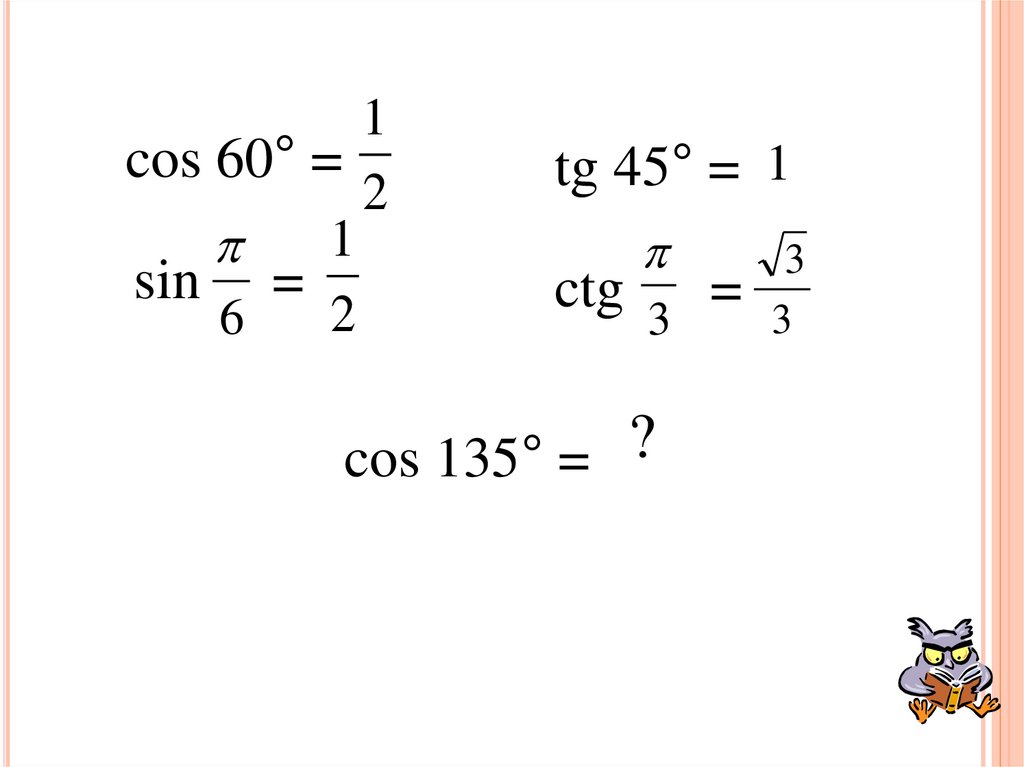










 Математика
Математика