Похожие презентации:
Корни натуральной степени из числа. Их свойства
1. Корни натуральной степени из числа. Их свойства.
презентация по математикедля студентов первого
курса
преподавателя Дегтяревой
А.А.
2. Цель занятия
Обеспечение усвоения понятия корнянатуральной степени из числа
Формирование представлений о свойствах
корней и действиях с корнями
Формирование умений преобразования корней
3.
Иррациональные выраженияИррациональным выражением относительно какой-либо
переменной называется выражение, в котором эта переменная
находится под знаком корня (радикала).
То есть, если говорить простыми словами, то
иррациональное выражение – это то выражение, которое
содержит в себе при записи знак корня.
Подобными корнями называются корни одной степени, имеющие
одинаковые подкоренные выражения.
Чтобы сложить или вычесть иррациональные выражения, нужно
записать их соответственно со знаком «+» или «-» и привести
подобные корни.
4.
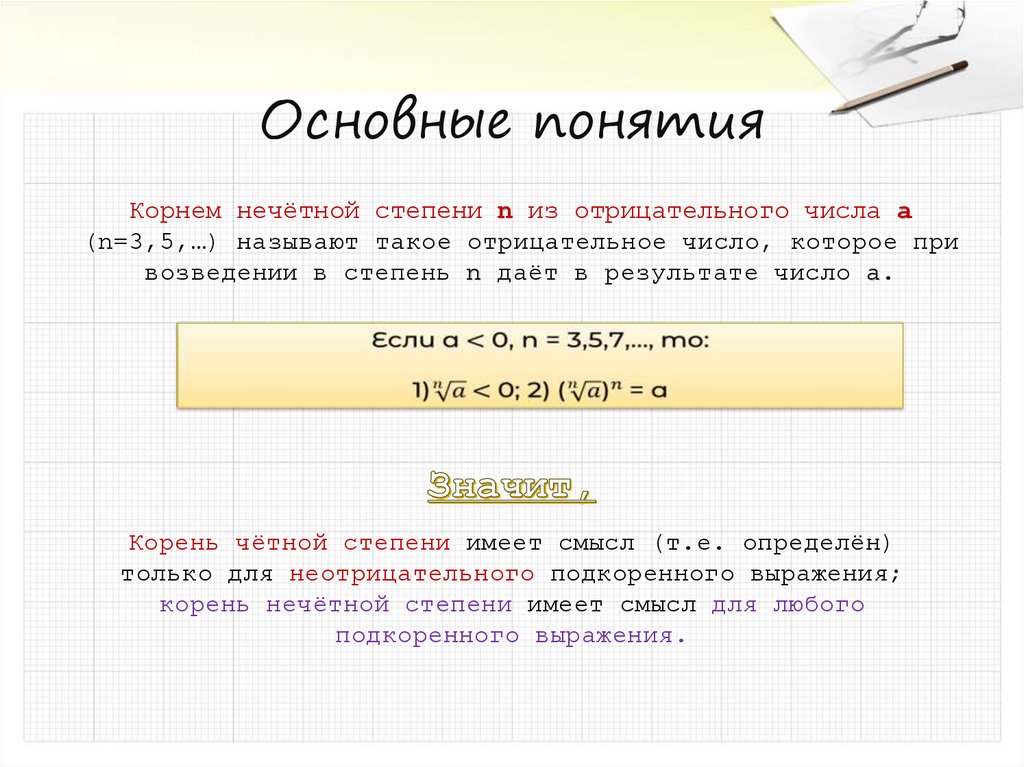
Основные понятия5.
Основные понятияКорнем нечётной степени n из отрицательного числа a
(n=3,5,…) называют такое отрицательное число, которое при
возведении в степень n даёт в результате число a.
Корень чётной степени имеет смысл (т.е. определён)
только для неотрицательного подкоренного выражения;
корень нечётной степени имеет смысл для любого
подкоренного выражения.
6.
Суть корней и степенейпри решении
Операция извлечения корня является обратной по отношению к
возведению в соответствующую степень.
Возведение в степень
Извлечение корня
7.
Решение примеров с корнями8.
Решение примеров с корнями9.
Свойства корней n-степени1. Корень n-степени из произведения неотрицательных
чисел равен произведению корней n-степени из этих чисел:
=
Пример:
2.
Чтобы извлечь корень из дроби, нужно извлечь
корень из числителя и знаменателя отдельно и первый
результат разделить на второй:
=
Пример:
10.
Свойства корней n-степени3. Если a ≥ 0, n =2,3,4,5,… и k – любое
число, то справедливо равенство:
натуральное
Пример:
4. Если a≥0, n и k - натуральные числа, большие 1, то
справедливо равенство:
Пример:
11.
Свойства корней n-степени5. Если показатели корня и подкоренного выражения
умножить или разделить на одно и то же отличное от нуля
число, то значение корня не изменится:
Пример:
6. Чтобы извлечь корень из степени,
которой делится на показатель корня, нужно
степени разделить на показатель корня:
Пример:
показатель
показатель
12.
ИтогиИтак, в презентации было разобрано:
Что такое иррациональные выражения
Основные понятия, которые необходимо знать при
работе с выражениями, содержащими корни и
степени
Операцию, с помощью которой происходит
извлечение корня
Как решаются примеры и уравнения со степенями и
корнями
Свойства корней
Написанные по презентации конспекты скидывайте мне.
Не забудьте про уравнения, которые вам нужно решить!












 Математика
Математика








