Основы логики

1. Основы логики.

2. Цели урока:

Познакомиться
1. с формами мышления.
2. С алгеброй высказываний
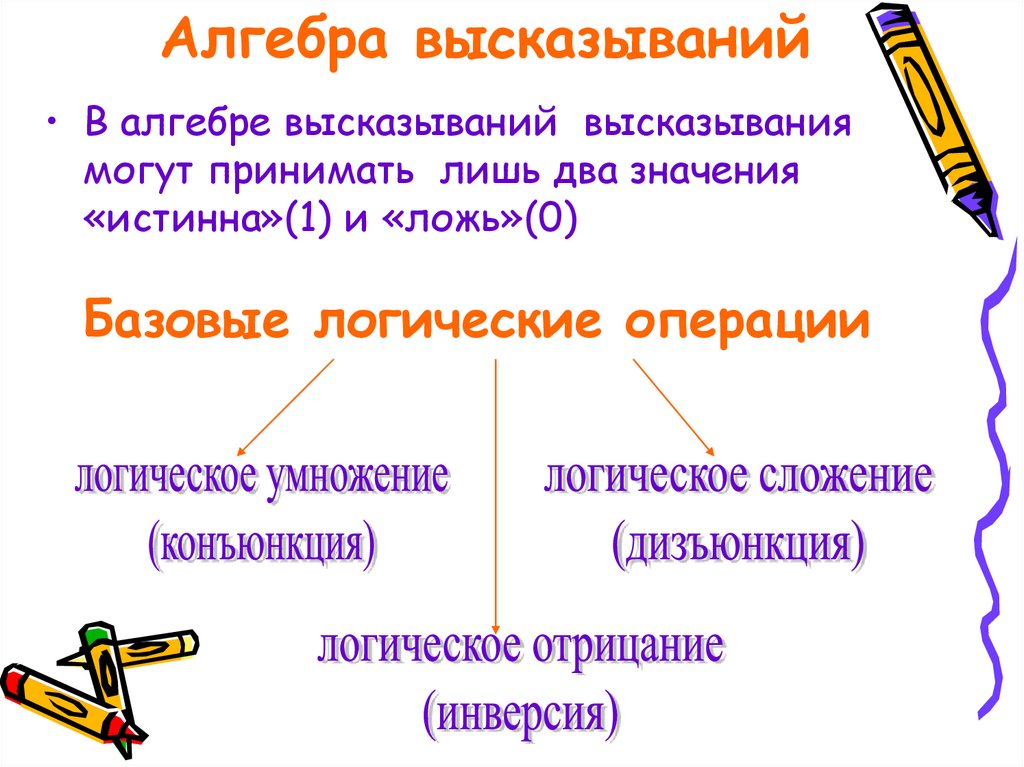
• Конъюнкция
• Дизъюнкция
• Инверсия
3. С таблицами истинности логических
выражений

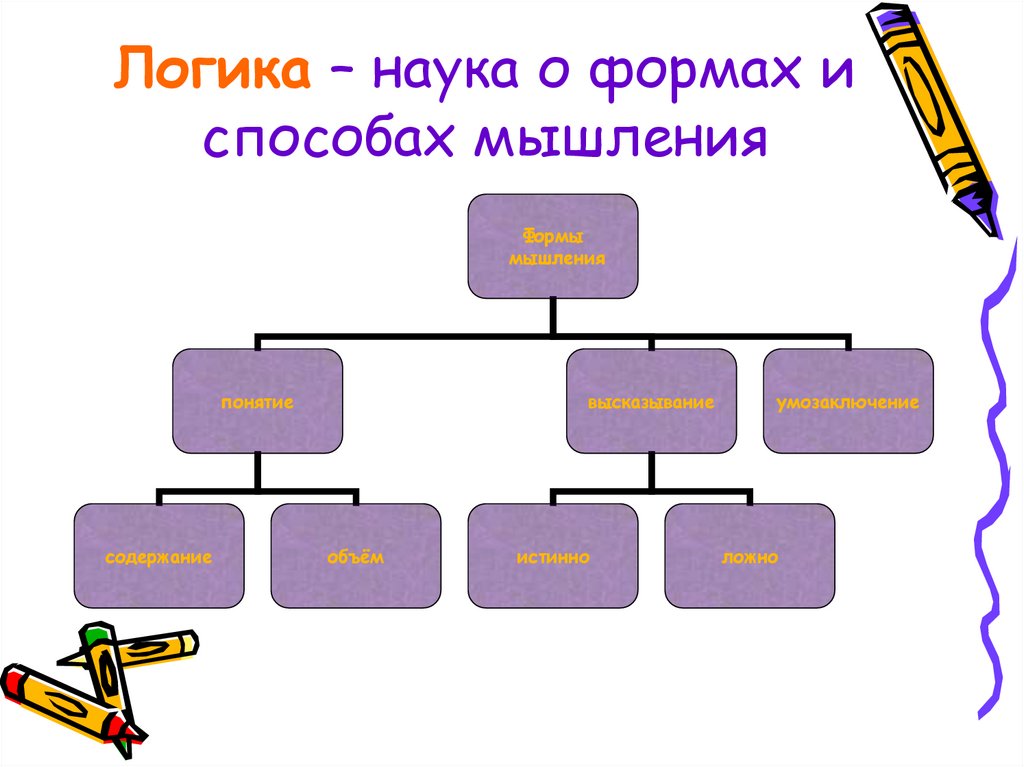
3. Логика – наука о формах и способах мышления

Формы
мышления
понятие
содержание
высказывание
объём
истинно
умозаключение
ложно

4.

Как математика оперирует числами, письменность буквами –
логика оперирует высказываниями.
Высказывание – повествовательное предложение,
относительно которого можно судить истинно(1) оно
или ложно(0).
Обозначаются высказывания латинскими буквами
Например:
X = Летом у школьников каникулы; Х=1 (высказывание истинно)
Y = Яблоки растут на березе; Y=0 (высказывание ложно)
F= «Ура, пришла весна! » – не высказывание т.к. не является
повествовательным предложением
Все приведенные высказывания являются простыми.

5.

Сложное высказывание получается
из простых при помощи логических
связок («И», «ИЛИ», «НЕ»).
Иначе они называются логическими операциями.
Сложные высказывания также будут истинными или
ложными.

6. Алгебра высказываний

• В алгебре высказываний высказывания
могут принимать лишь два значения
«истинна»(1) и «ложь»(0)
Базовые логические операции

7.

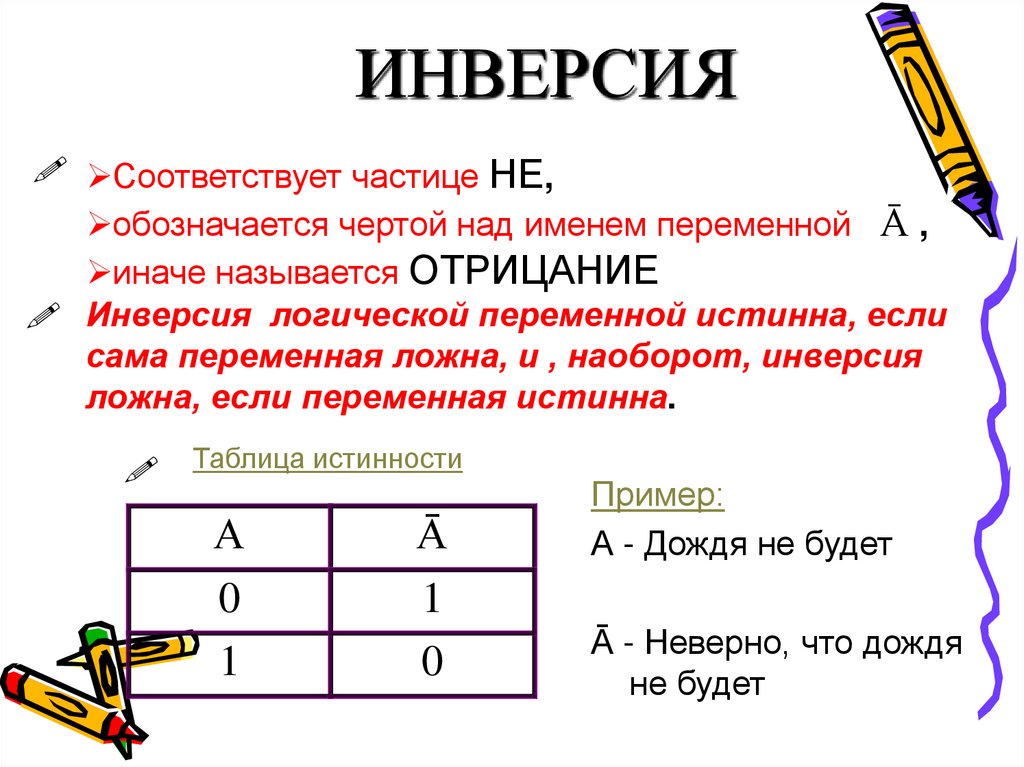
ИНВЕРСИЯ
Соответствует частице НЕ,
обозначается чертой над именем переменной Ā ,
иначе называется ОТРИЦАНИЕ
Инверсия логической переменной истинна, если
сама переменная ложна, и , наоборот, инверсия
ложна, если переменная истинна.
Таблица истинности
А
0
1
Ā
1
0
Пример:
А - Дождя не будет
Ā - Неверно, что дождя
не будет

8.

КОНЪЮНКЦИЯ
Соответствует союзу И,
обозначается знаками ^, &, *
иначе называется ЛОГИЧЕСКОЕ УМНОЖЕНИЕ.
Конъюнкция двух логических переменных истинна
тогда и только тогда, когда оба высказывания
истинны.
Таблица истинности:
Пример:
А
В
А*В
А - Дождя не будет.
0
0
0
В - Небо голубое.
0
1
0
А&В - Дождя не будет и
1
0
0
1
1
1
небо голубое.

9.

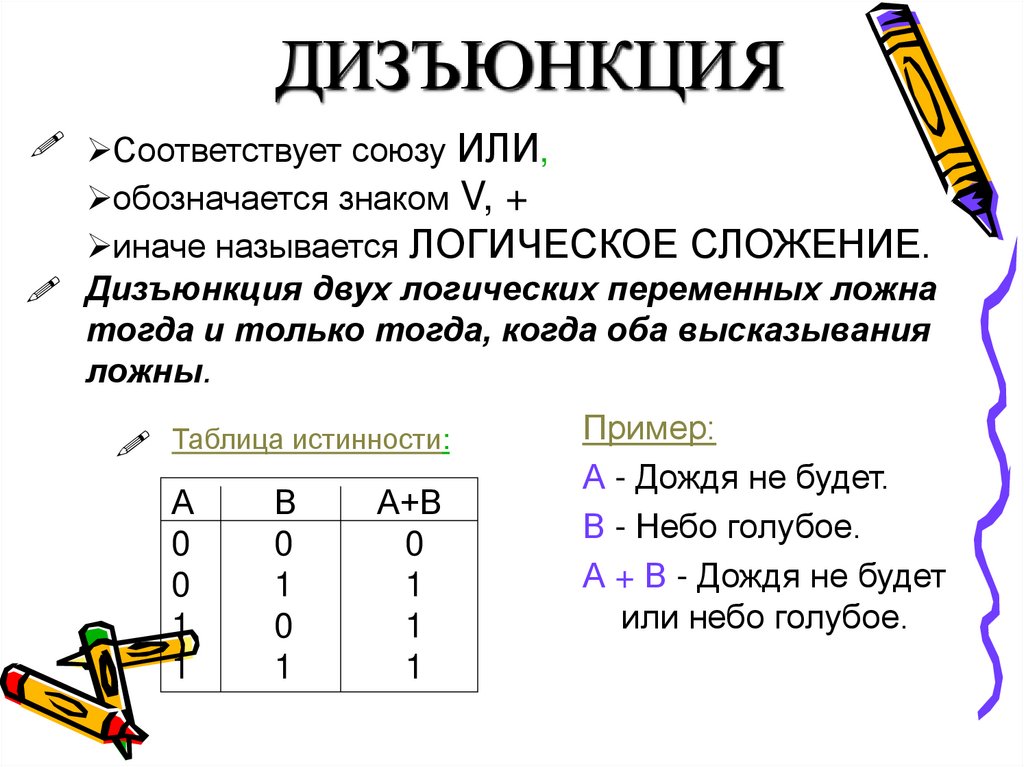
ДИЗЪЮНКЦИЯ
Соответствует союзу ИЛИ,
обозначается знаком V, +
иначе называется ЛОГИЧЕСКОЕ СЛОЖЕНИЕ.
Дизъюнкция двух логических переменных ложна
тогда и только тогда, когда оба высказывания
ложны.
Таблица истинности:
А
0
0
1
1
В
0
1
0
1
А+В
0
1
1
1
Пример:
А - Дождя не будет.
В - Небо голубое.
А + В - Дождя не будет
или небо голубое.

10.

Значения логической функции для
разных сочетаний значений
входных переменных
( наборов входных переменных)
задаются таблицей истинности.
Количество наборов входных переменных Q определяется
по формуле: Q = 2n ,
где n - количество входных переменных

11. Количество строк кол-во переменных + кол-во операций = кол-во столбцов

Логические переменные
Знаки логических операций
2 1 Количество строк
n
кол-во переменных +
кол-во операций =
кол-во столбцов

12.

Приоритет логических операций:
Инверсия,
Конъюнкция,
Дизъюнкция.

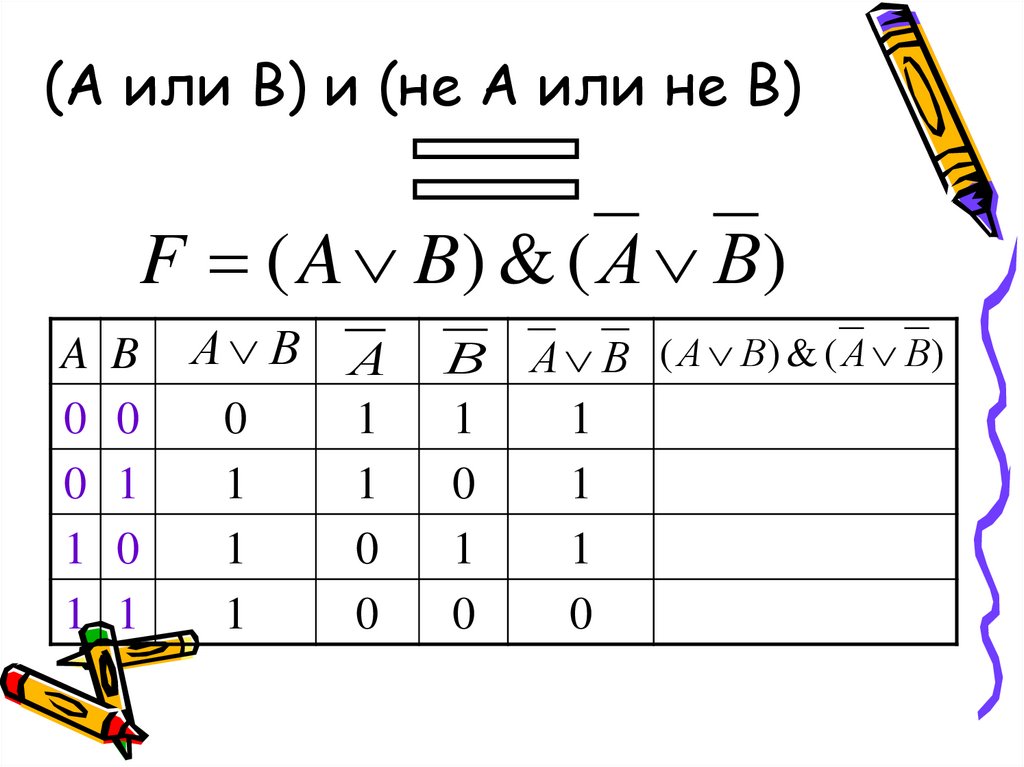
13. (А или В) и (не А или не В)

F ( A B) & ( А В)
A B
А В А
В А В ( А В) & ( А В)

14. (А или В) и (не А или не В)

F ( A B) & ( А В)
A B
0
0
1
1
А В А
В А В ( А В) & ( А В)

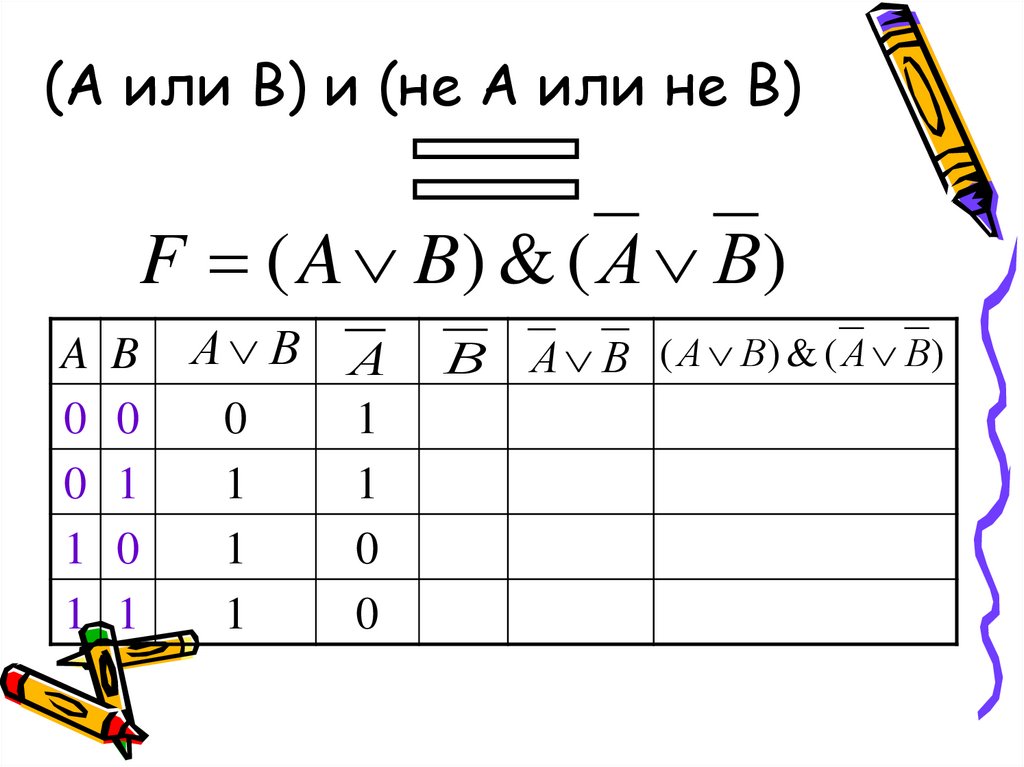
15. (А или В) и (не А или не В)

F ( A B) & ( А В)
A
0
0
1
1
B
0
1
0
1
А В А
В А В ( А В) & ( А В)

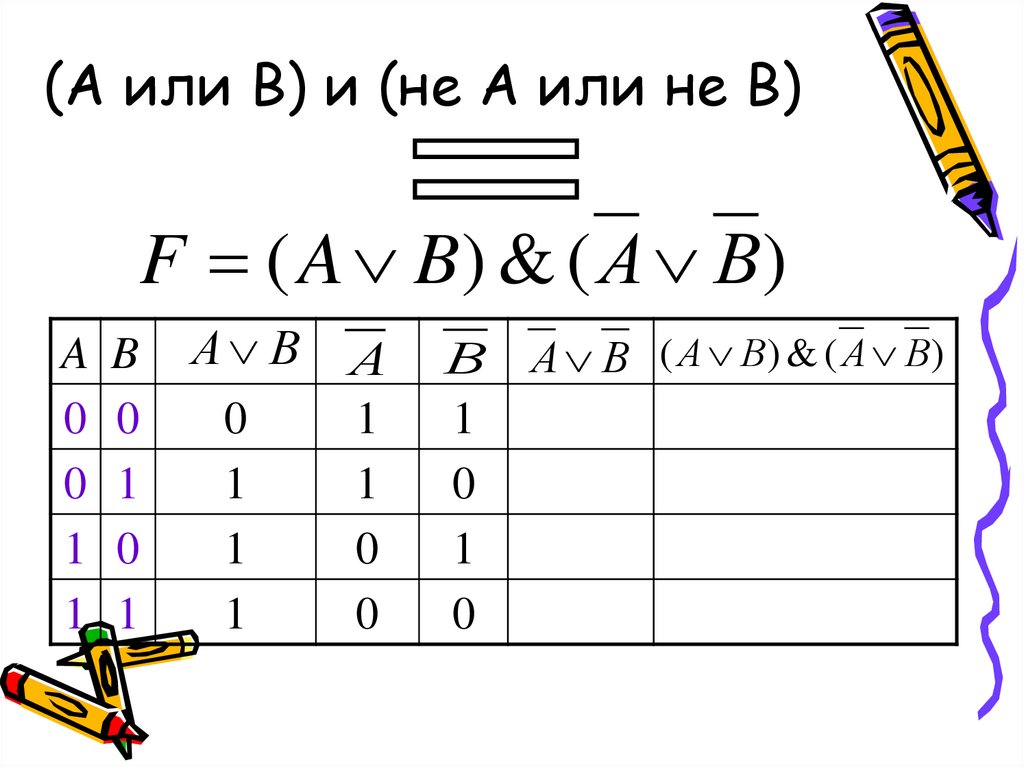
16. (А или В) и (не А или не В)

F ( A B) & ( А В)
A
0
0
1
1
B
0
1
0
1
А В А
0
1
1
1
В А В ( А В) & ( А В)

17. (А или В) и (не А или не В)

F ( A B) & ( А В)
A
0
0
1
1
B
0
1
0
1
А В А
0
1
1
1
1
1
0
0
В А В ( А В) & ( А В)

18. (А или В) и (не А или не В)

F ( A B) & ( А В)
A
0
0
1
1
B
0
1
0
1
А В А
0
1
1
1
1
1
0
0
В А В ( А В) & ( А В)
1
0
1
0

19. (А или В) и (не А или не В)

F ( A B) & ( А В)
A
0
0
1
1
B
0
1
0
1
А В А
0
1
1
1
1
1
0
0
В А В ( А В) & ( А В)
1
1
0
1
1
1
0
0

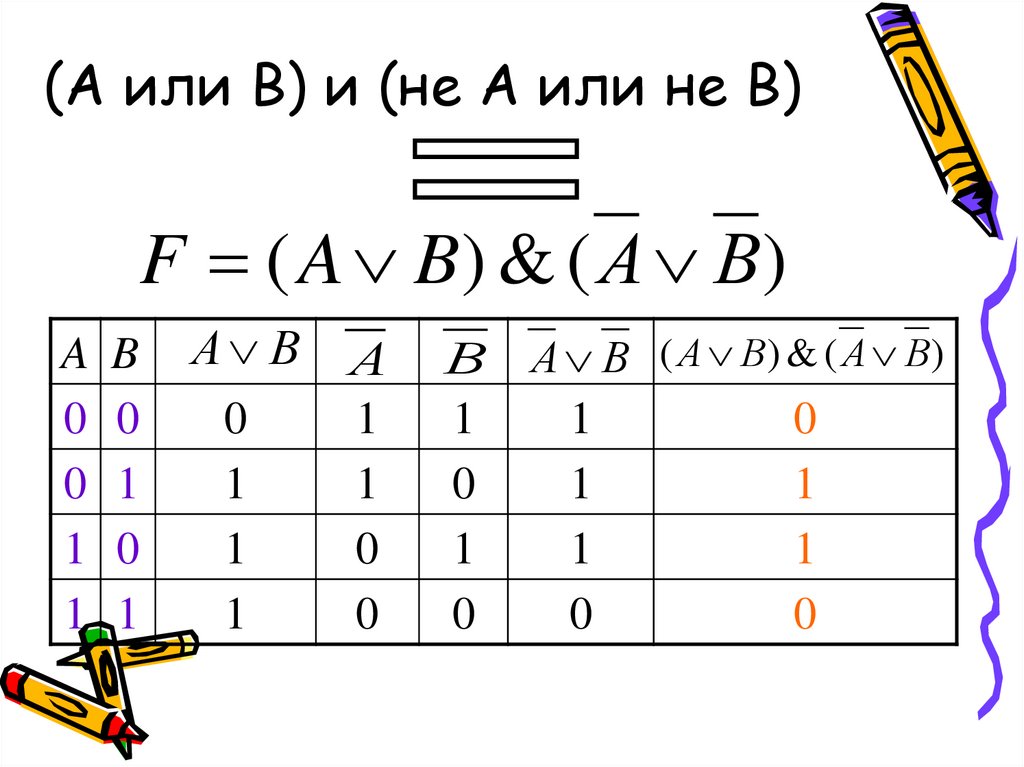
20. (А или В) и (не А или не В)

F ( A B) & ( А В)
A
0
0
1
1
B
0
1
0
1
А В А
0
1
1
1
1
1
0
0
В А В ( А В) & ( А В)
1
1
0
0
1
1
1
1
1
0
0
0

21.

22.

Таблица истинности функции
логического отрицания
А
F=А
0
1
1
0

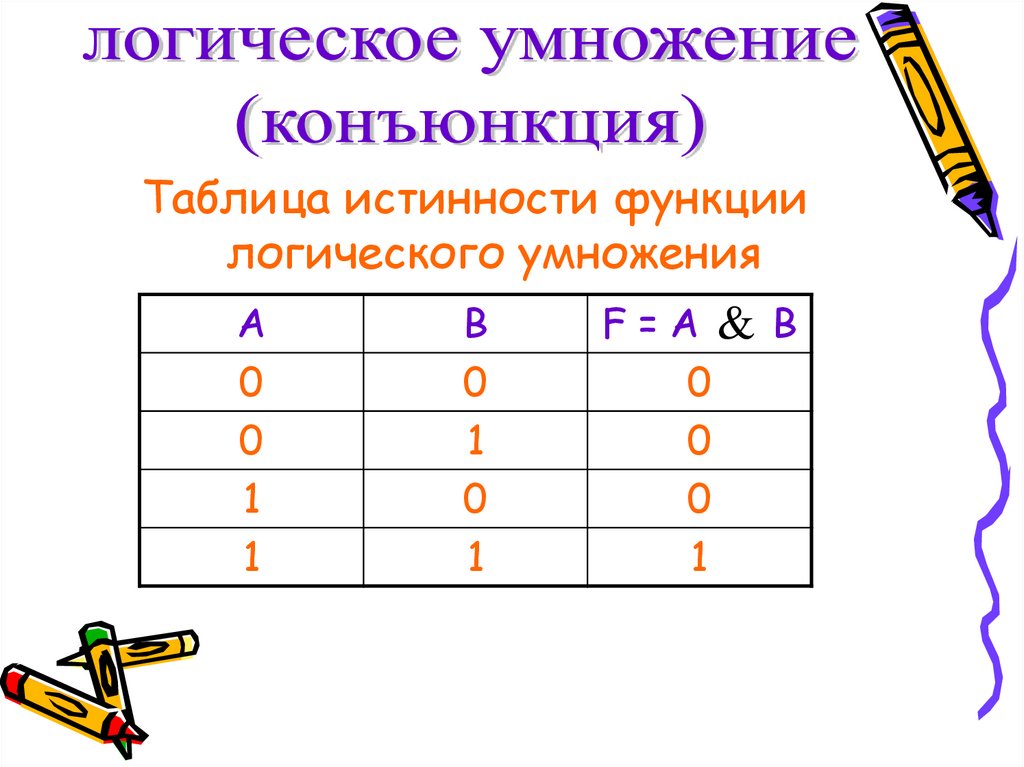
23.

Таблица истинности функции
логического умножения
А
0
0
1
1
В
0
1
0
1
F=А & В
0
0
0
1

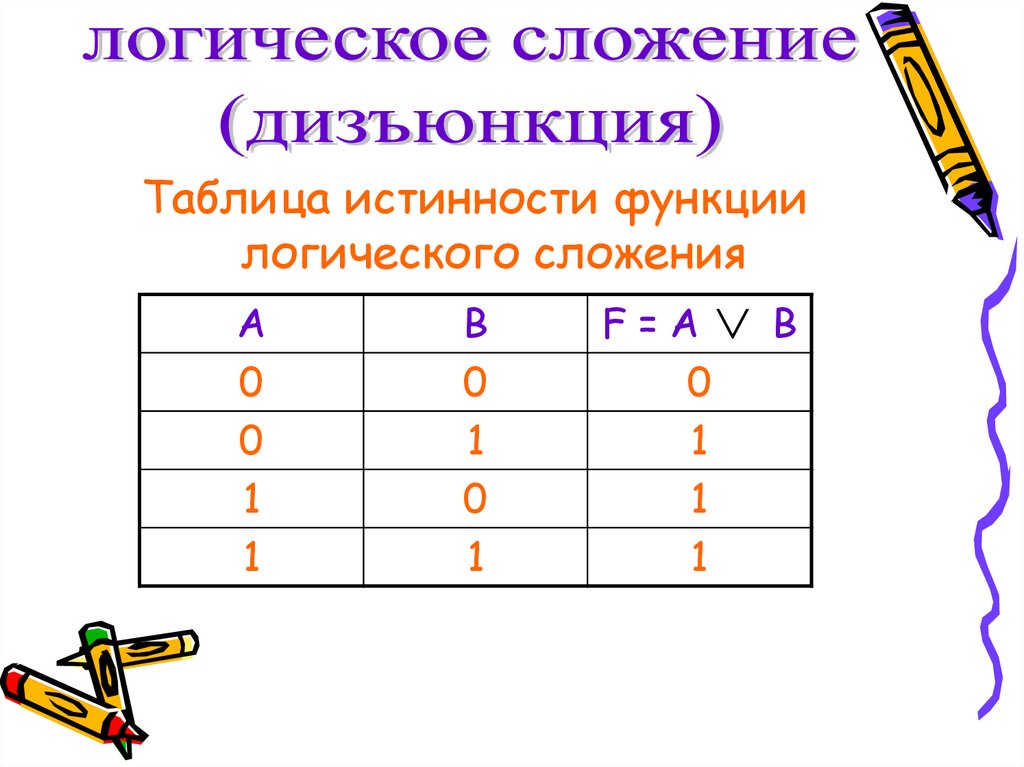
24.

Таблица истинности функции
логического сложения
А
0
0
1
1
В
0
1
0
1
F=А
0
1
1
1
В

25. Домашнее задание

§1.3, п.1.3.1-1.3.3
• Выписать и выучить определение
понятие, высказывание,
умозаключение, конъюнкция,
дизъюнкция, инверсия.
• Выучить таблицы истинности
основных логических операций