Квадратные уравнения и способы их решения

1. Повторение.

2.

3. ax2+bx+c

• Повторение.
Как разложить
квадратный
трёхчлен на
множители?
2
ax +bx+c

4. Где, x1 иx2 ax2+bx+c=0

2
ax +bx+c=a(x-x1 )(x-x2)
Где, x1 иx2
Корни уравнения
2
ax +bx+c=0

5. Разложите квадратный трёхчлен на множители

х2-8х+7=
−х2+11х−30=
2х2-7х+6=
3х2-8х+7=

6. Проверь себя:

X1 = 1; X2 = 7
х2-8х+7=0
х2-8х+7=(х-1)(х-7)
−х2−7х+8=0 /:(-1); х2 +7х−8=0;
X1 = -8; X2= 1 ;
−х2−7х+8=-(х+8)(х-1)
2х2-7х+6=2(х-1,5)(х-2)
-3х2-8х+3= -3(х- ⅓ )(х+3)

7.

Повторение.
1. Какие неравенства соответствуют промежуткам:
0;
;5
3;5
; 5
х 0
х 5
3 х 5
х 5

8.

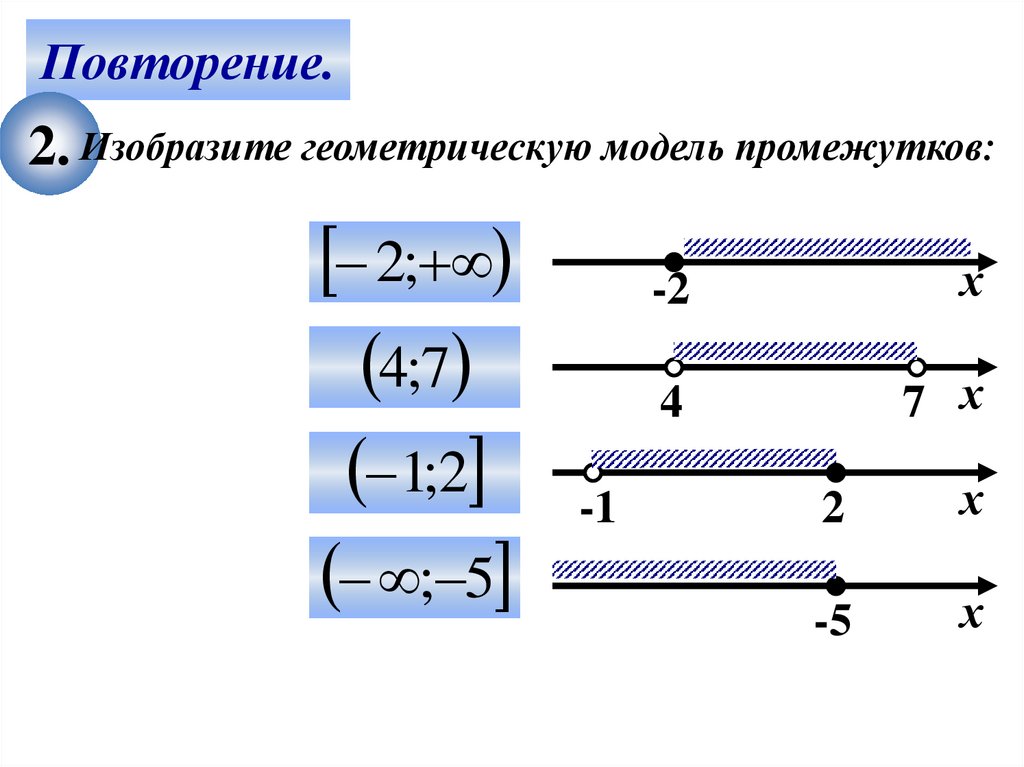
Повторение.
2. Изобразите геометрическую модель промежутков:
2;
4;7
1;2
; 5
-1
-2
х
4
7 х
2
х
-5
х

9.

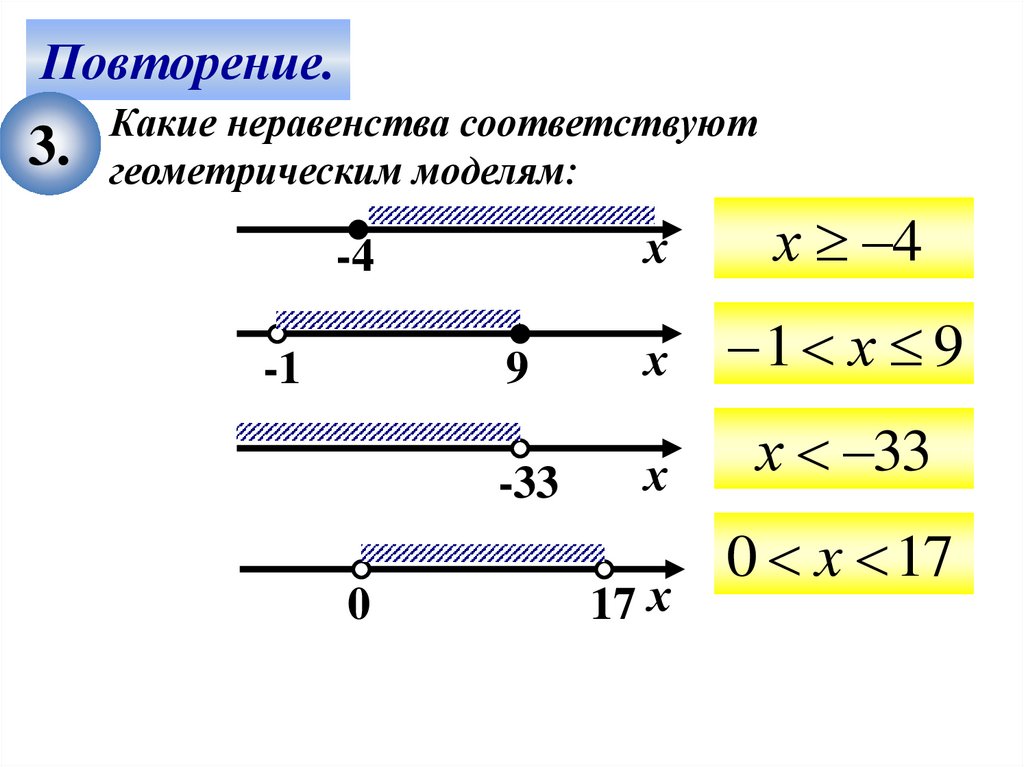
Повторение.
3.
Какие неравенства соответствуют
геометрическим моделям:
-4
-1
9
-33
0
х
х 4
х
1 х 9
х
х 33
17 х
0 x 17

10.

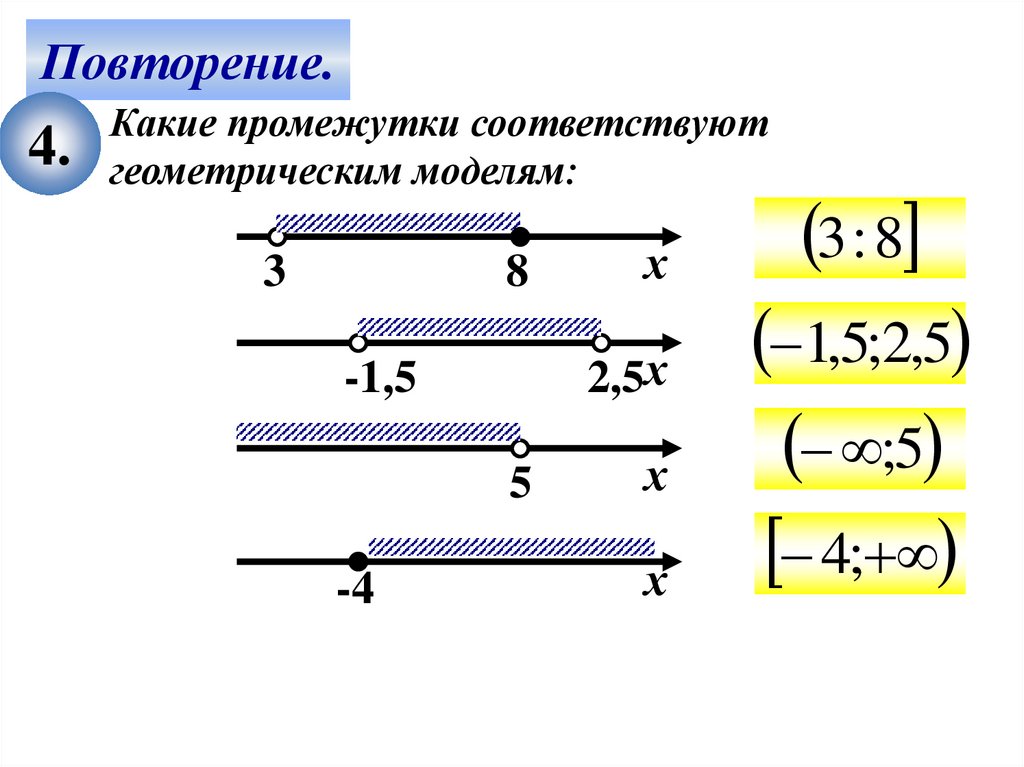
Повторение.
4.
Какие промежутки соответствуют
геометрическим моделям:
3
8
2,5х
-1,5
5
-4
х
х
х
3 : 8
1,5;2,5
;5
4;

11.

Неравенства бывают:
линейные
квадратные
рациональные
иррациональные

12. Линейные неравенства

Определения:
1) Запись вида а>в; а≥в или а<в; а≤в называется
неравенством
2) Неравенства вида а≥в, а≤в называются
нестрогими.
3) Неравенства вида а>в, а<в называются
строгим
4) Решением неравенства с одной переменной
называется то значение переменной, которое
обращает его в верное числовое
неравенство

13. Линейные неравенства

Правила:
1) Любой член неравенства можно
переносить из одной части
неравенства в другую, изменив его
знак на противоположный, при этом
знак неравенства не изменится.

14. Линейные неравенства

Правила:
2) Обе части неравенства можно
умножить или разделить на одно и
тоже положительное число, при этом
знак неравенства не изменится.

15. Линейные неравенства

Правила:
3) Обе части неравенства можно
умножить или разделить на одно и
тоже отрицательное число, при этом
знак неравенства изменится на
противоположный.

16. Решим неравенство: 16х>13х+45

Решим неравенство: 16х>13х+45
Решение: 16х>13х+45
16х-13х > 45
слагаемое 13х с противоположным знаком
перенесли в левую часть неравенства
3х > 45
х > 15
15
привели подобные слагаемые
поделили обе части неравенства на 3
х
Ответ: (15;+∞)

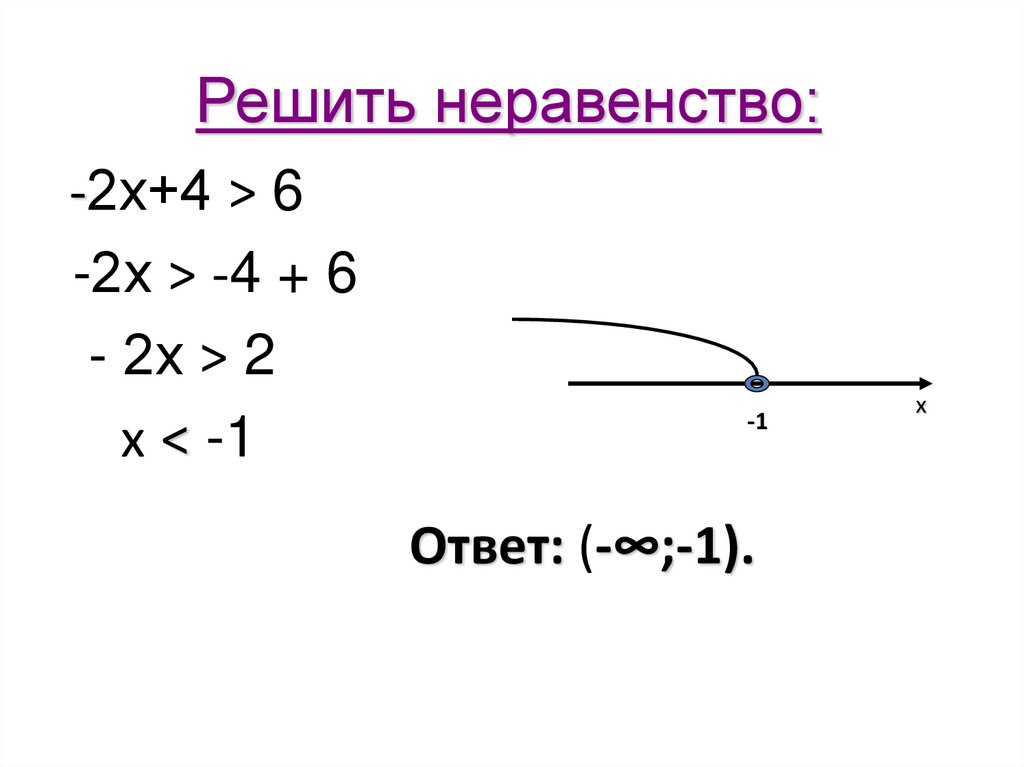
17. Решить неравенство:

-2х+4 > 6
-2х > -4 + 6
- 2х > 2
х < -1
-1
Ответ: (-∞;-1).
х

18. Решить неравенства :

1) х+2 ≥ 2,5х-1;
2) х²+х < х(х-5)+2;

19. Проверь себя:

2) х²+х < х(х-5)+2
1) х+2 ≥ 2,5х-1
х²+х < х²- 5х +2
х-2,5х ≥ -2 -1
- 1,5х ≥ - 3 /:(- 1,5) х² +х - х²+5х < 2
6х < 2 /:6
х≤2
х<⅓
2
⅓ х
х
Ответ: (-∞;2]
Ответ: (-∞;⅓)

20.

Решаем систему неравенств.
Решить систему неравенств – найти значение
переменной, при котором верно каждое из
неравенств системы.
2 х 1 6, 2 х 6 1,
5 3x 13 3x 13 5
2 х 7 / : 2,
х
3,5,
3x 18 / : ( 3)
x 6
3,5
6 х
Ответ: (3,5;6)