Прямоугольные треугольники и некоторые их свойства

1. ПРЯМОУГОЛЬНЫЕ ТРЕУГОЛЬНИКИ

И НЕКОТОРЫЕ ИХ СВОЙСТВА.
Геометрия 7 класс
Часть 2
Учитель математики
МОУ “Оленовская школа №2
Волновахского района”
Прохоренко Ирина Ивановна

2.

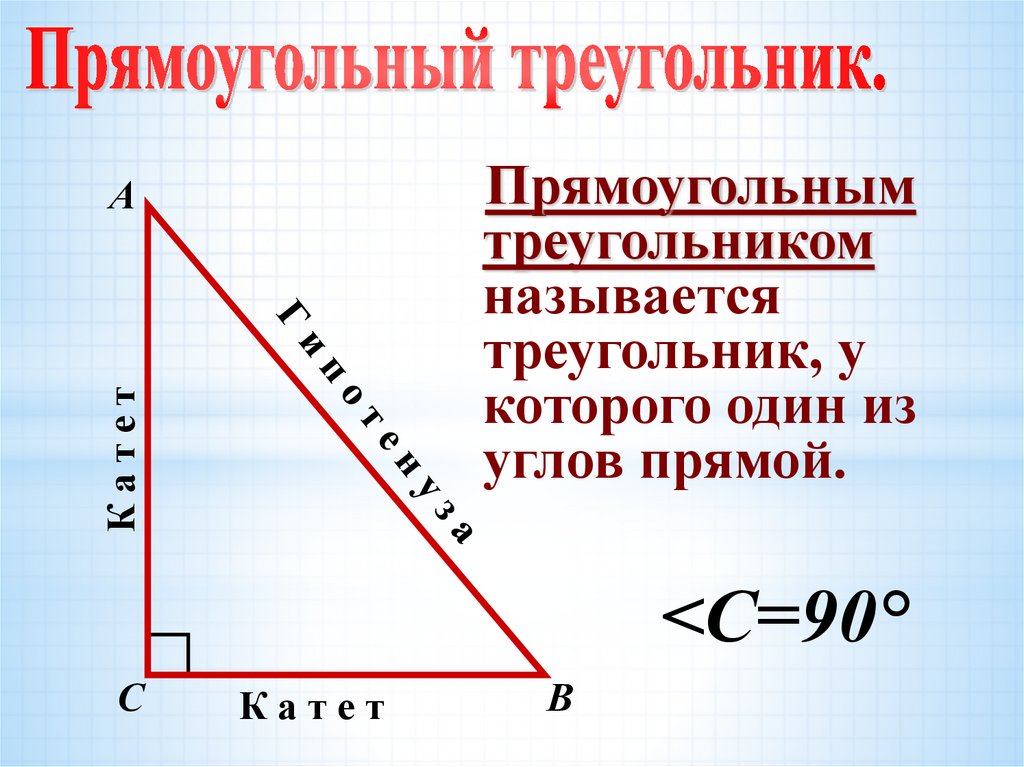
Прямоугольным
треугольником
называется
треугольник, у
которого один из
углов прямой.
Катет
А
<С=90°
С
Катет
В

3. Гипотенуза и катет

«Гипотенуза» и «катет»- слова
греческие.
«Гипотенуза» -в переводе
«натянутая»
«Катет»-в переводе «отвес»
*Гипотенуза и катет

4.

Свойство 1
Сумма двух острых углов прямоугольного
треугольника равна 90º
A
Доказательство:
ΔABC – прямоугольный, С – прямой.
По теореме о сумме углов треугольника:
A+ B + C = 180º. Отсюда
A+ B = 180º - C = 90º,
что и требовалось доказать
C
B

5. Например:

А
1.
Дано: ∆ АВС <С=90°,<А=56°
56°
С
Найти: <В
В
Решение: так как <А+<В=90°(свойство острых углов
прямоугольного треугольника) => <В=90°- <А= 34°
Ответ: 34°

6.

Свойство 2
Катет прямоугольного треугольника, лежащий
против угла в 30º , равен половине
гипотенузы.
B
Доказательство:
ΔАВD= ΔАBС (по построению).
Получим ΔBСD - равносторонний, в котором
B = D = С 60º, поэтому DC=BC. Но AC
=1/2 DC. Следовательно, AC=1/2 BC, что и
требовалось доказать.
30º 30º
60º
D
A
C

7.

Например:
А
2.
Дано: ∆ АВС <С=90°,<А=30° ВС=4 см
Найти: АВ
Решение: по свойству 2, ВС=1/2 АВ =>
АВ=2∙ВС, АВ=8 см
Ответ: 8 см
30°
С
Р
4см
В
Дано: ∆ PSR <S=90°,
SR=4,2 см, PR=8,4 cм
3.
R
Найти: <P, <R
Решение: Т.к. в треугольнике
4,2см < S=90° и РR=2 RS ( катет в
два раза меньше гипотенузы),
S то <Р =30°, а значит
< R =90°- <Р=60°
Ответ: 30°, 60°

8.

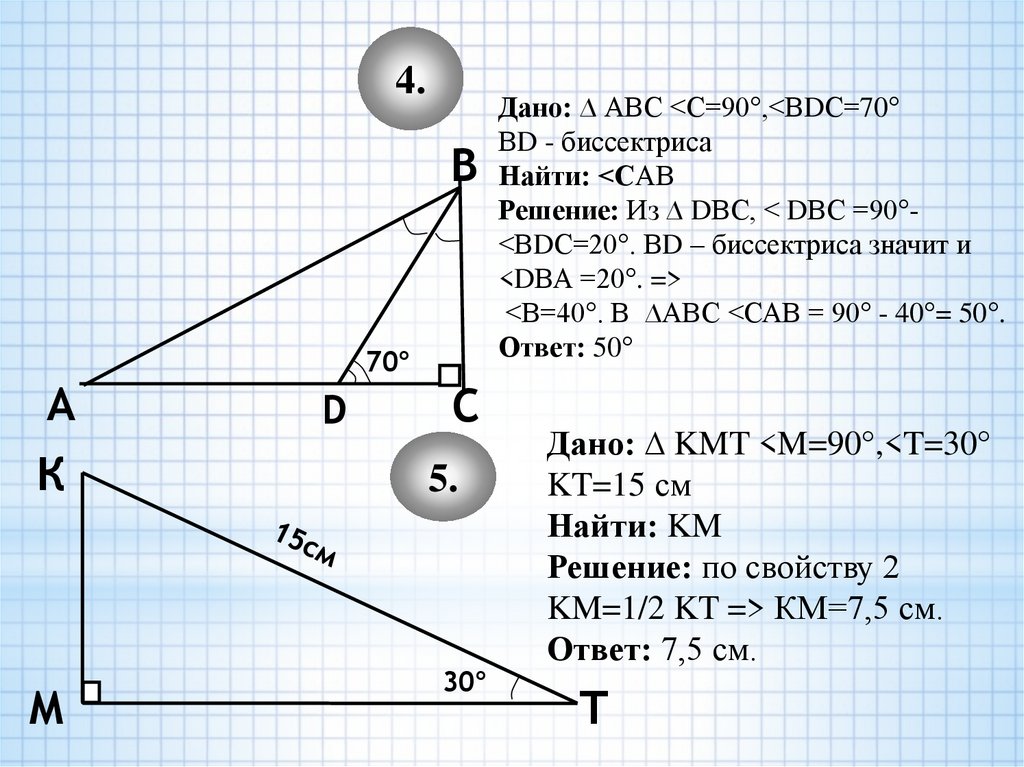
4.
В
А
К
М
70°
D
С
5.
30°
Дано: ∆ АВС <С=90°,<ВDС=70°
ВD - биссектриса
Найти: <САВ
Решение: Из ∆ DВС, < DВС =90°<ВDС=20°. ВD – биссектриса значит и
<DВА =20°. =>
<В=40°. В ∆АВС <САВ = 90° - 40°= 50°.
Ответ: 50°
Дано: ∆ KMT <M=90°,<T=30°
KT=15 см
Найти: KM
Решение: по свойству 2
KM=1/2 KT => КМ=7,5 см.
Ответ: 7,5 см.
Т

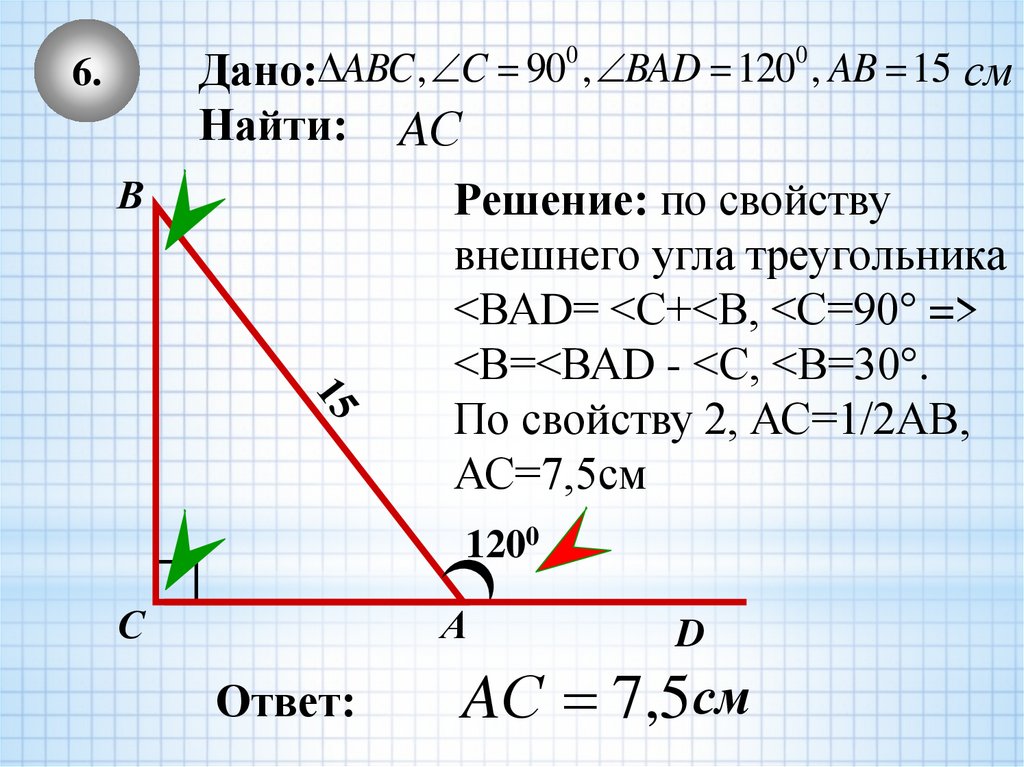
9.

0
0
ABC
,
C
90
,
BAD
120
, AB 15 см
Дано:
6.
Найти:
В
AС
Решение: по свойству
внешнего угла треугольника
<ВАD= <С+<В, <С=90° =>
<В=<ВАD - <С, <В=30°.
По свойству 2, АС=1/2АВ,
АС=7,5см
1200
С
А
Ответ:
D
AС 7,5см

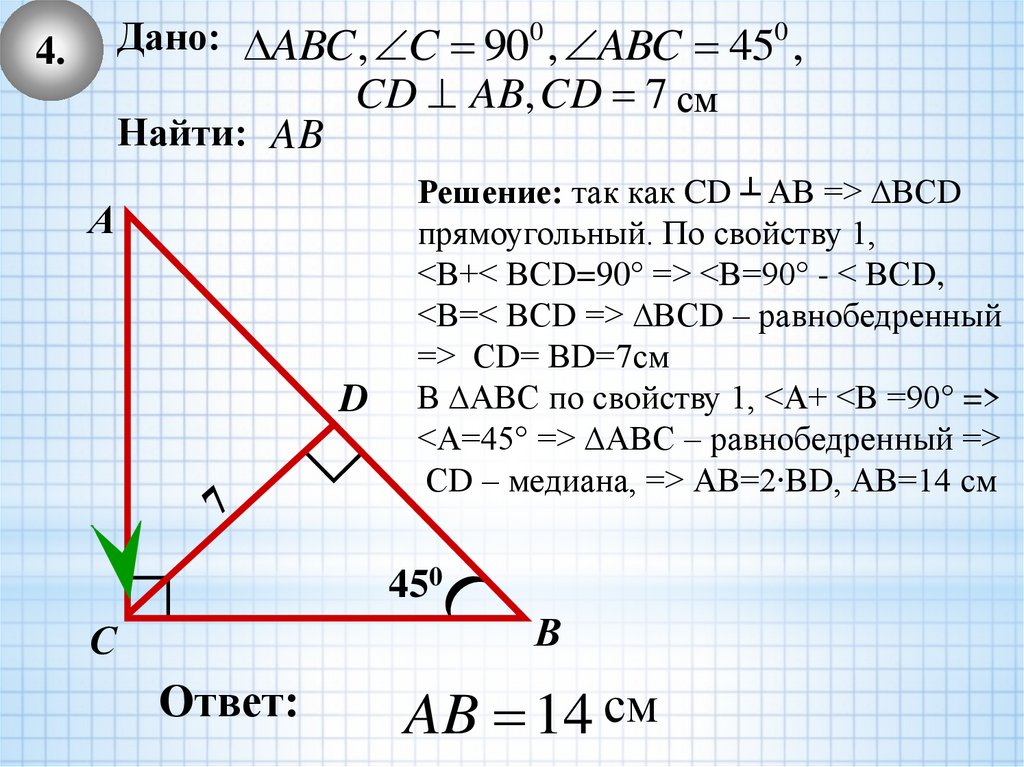
10.

Дано: ABC , C 900 , ABC 450 ,
CD AB, CD 7 см
Найти: AB
4.
А
D
Решение: так как CD ┴ АВ => ∆ВСD
прямоугольный. По свойству 1,
<В+< ВСD=90° => <В=90° - < ВСD,
<В=< ВСD => ∆ВСD – равнобедренный
=> СD= ВD=7см
В ∆АВС по свойству 1, <А+ <В =90° =>
<А=45° => ∆АВС – равнобедренный =>
СD – медиана, => АВ=2∙ВD, АВ=14 см
450
В
С
Ответ:
AB 14 см

11.

5.
Дано: ∆АВС;
< С=900 <ВАD=1200-внешний
АС+АВ=16см.
Найти: АС и АВ.
С
1200
D
А
Решение:
по свойству внешнего угла
<САD= <С+<В, <С=90° =>
В <В=<САD - <С, <В=30°.
По свойству 2, АС=1/2АВ. По условию АС+АВ=18см;
1/2АВ+АВ=16; 3/2АВ=16; АВ= 16:3/2= 16∙2/3=12(см);
значит АС=18-12=6(см).
Ответ:
6см; 12см

12. Домашнее задание

* Домашнее задание
Изучить § 3, п. 35
Решить № 254,256,257
1.
Один из острых углов прямоугольного треугольника на 340 меньше
от другого. Найти эти углы.
2.
В прямоугольном треугольнике СFO гипотенуза СО = 42 см,
<О=600. Найти катет FO.
3.
Найдите угол С треугольника АВС, если угол А равен 650, угол В
равен 240.
4.
5.
В прямоугольном треугольнике угол А равен 490. Найдите угол В.
Найдите острые углы прямоугольного треугольника, если один
угол больше второго на 120.