Похожие презентации:
Свойства пространства-времени и интегралы состояния: четность
1.
Лекция 16СВОЙСТВА ПРОСТРАНСТВА-ВРЕМЕНИ
И ИНТЕГРАЛЫ СОСТОЯНИЯ: ЧЕТНОСТЬ
2.
→Предположим, что в пространстве имеется центр
симметрии. Это означает, что состояние системы,
состоящей из N частиц, не изменится при замене знака у
-r j
координат всех частиц, т.е. при замене r j
(j = 0, 1, …, N). Операция такого рода называется
инверсией, и можно ввести оператор инверсии ˆ :
ˆ f ( ) f ( ) .
Поскольку при наличии центра симметрии в пространстве
состояние системы не изменяется, гамильтониан системы
должен коммутировать с оператором инверсии:
ˆ H
ˆ ˆ .
ˆ H
(16.1)
Из (16.1) следует, что должен быть некоторый интеграл
состояния системы. В данном случае его называют
четностью состояния. Выясним, что это означает.
Предположим, что решение уравнения Шредингера для
стационарных состояний нам известно, в частности,
известна волновая функция Ψ(ξ). Поскольку операторы
и Hˆ коммутируют, у них должна быть общая система
собственных функций (см. окончание лекции 5).
ˆ
3.
Следовательно, волновая функция Ψ(ξ) будет собственнойфункцией и оператора инверсии ˆ :
ˆ =πΨ ,
πΨ
(16.2)
где π - собственное значение. Подействуем на это
уравнение оператором ˆ еще раз и учтем, что двукратное
действие этого оператора является тождественным
2
ˆ
=1 .
преобразованием, т.е.
ˆ = π ( πΨ)
ˆ
πˆ (πΨ)
πˆ 2Ψ = π πΨ
.
Ψ = π 2Ψ π 2 = 1 π = ±1
ˆ
ξ) ≡Ψ( -ξ
)= ±
Ψ( ξ
).
В итоге: πΨ(
Это означает: когда Ψ( -ξ) = +Ψ( ξ) , волновая функция
четная, а когда Ψ( -ξ) = -Ψ( ξ) - нечетная. Говорят, что
волновая функция обладает определенной четностью и это
ее свойство и будет интегралом состояния – четностью.
4.
Пример 1. Квантовая система – одномерный гармоническийосциллятор с массой m и частотой колебаний ω.
В этом случае гамильтониан имеет вид:
2
2
2
d
m
2
Hˆ
x
.
2m dx 2
2
Видно, что в точке 0 имеется центр симметрии, так как
Hˆ ( x ) Hˆ ( x ) ˆ Hˆ Hˆ ˆ . Следовательно, состояния такого
осциллятора должны обладать определенной четностью. И
действительно, можно показать, что решение уравнения
ˆ
x) = E Ψ( x) дает волновые функции Ψn(x),
Шредингера HΨ(
зависящие от квантового числа n = 0, 1, 2, …, и оно будет
определять четность состояний:
Ψn(-x) = (-1)n Ψn(x).
В итоге, состояния квантового осциллятора с четными
значениями n = 0, 2, … будут четными, а с нечетными
значениями n = 1, 3, … - нечетными.
5.
Пример 2. Квантовая система – частица, движущаяся вполе центральных сил.
В этом случае потенциальная энергия частицы зависит
только от r r x y z . Гамильтониан в этом случае
при замене r r изменяться не будет, и четность должна
быть интегралом состояния. Можно показать, что в данной
задаче в переменных (r, θ, φ) волновая функция имеет вид:
( r, , ) R( r )Ylm ( , ) ,
где вид функции R(r) зависит от вида потенциальной
энергии и находится из уравнения Шрёдингера, а Ylm ( , ) это уже известная нам сферическая функция с известными
свойствами. При операции инверсии r r в сферической
системе координат r r, , :
ˆ ( r ) ( r ) R( r )Ylm ( , )
( 1)l R( r )Y ( , ) ( 1)l ( r ) ( r ) .
2
2
lm
2
l
6.
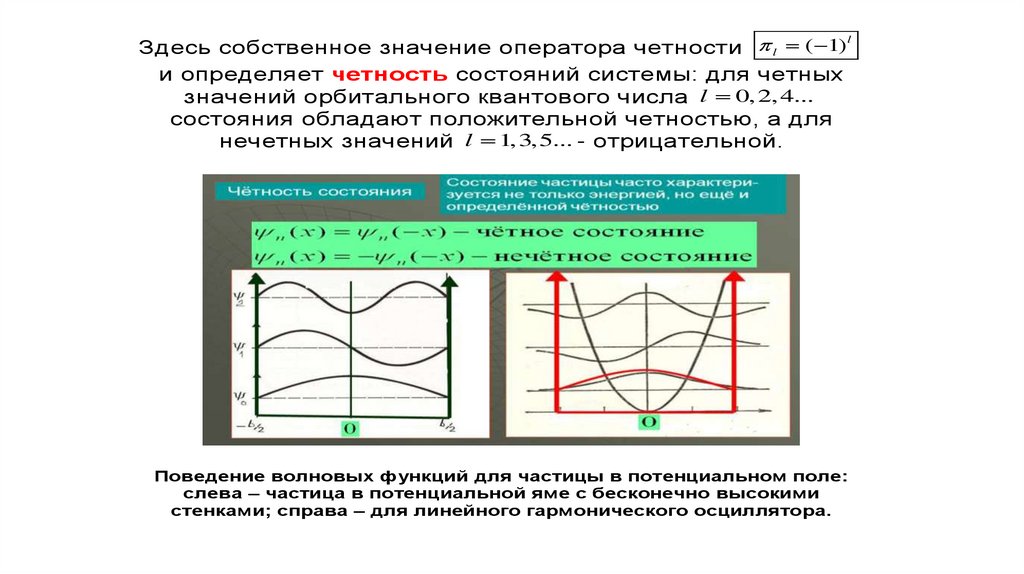
lЗдесь собственное значение оператора четности l ( 1)
и определяет четность состояний системы: для четных
значений орбитального квантового числа l 0, 2, 4...
состояния обладают положительной четностью, а для
нечетных значений l 1, 3, 5... - отрицательной.
Поведение волновых функций для частицы в потенциальном поле:
слева – частица в потенциальной яме с бесконечно высокими
стенками; справа – для линейного гармонического осциллятора.
7.
Предположим теперь, что имеется система частиц всиловом поле, имеющем центр симметрии, и частицы
взаимодействуют друг с другом. В этом случае
гамильтониан будет также включать слагаемое
1
2
N
N
Φ(ij
i =1 j =1( i ≠j)
rij ) , где Φ(ij
rij ) - потенциальная энергия
взаимодействия i-ой и j-ой частиц, rij ri - r j - расстояние
между ними (см. вид гамильтониана системы (9.9)).
Возникает вопрос: останется ли гамильтониан
симметричным и будет ли сохраняться четность? Для
разных типов взаимодействия (электромагнитного,
сильного и слабого) ответ был получен в 1956 г. физикамитеоретиками Т.Ли и Ч.Янгом совместно с физикомэкспериментатором Ц.Ву. Они проверили, что есть много
экспериментальных свидетельств относительно
электромагнитного и сильного взаимодействия: они
четность сохраняют. Однако для слабого
взаимодействия, из-за которого почти все наблюдаемые
элементарные частицы и многие атомные ядра
нестабильны и распадаются, таких доказательств
не было.
8.
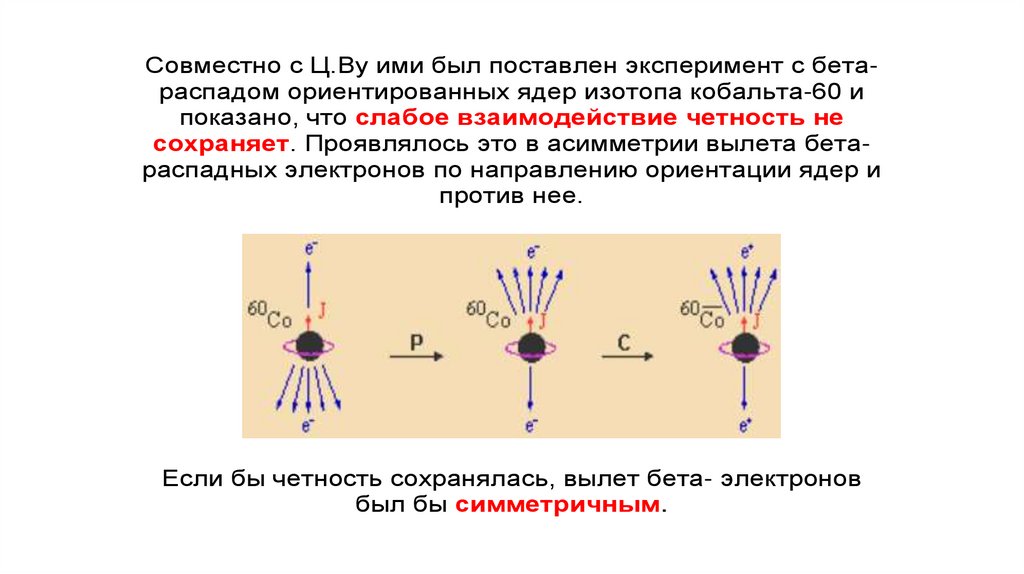
Совместно с Ц.Ву ими был поставлен эксперимент с бетараспадом ориентированных ядер изотопа кобальта-60 ипоказано, что слабое взаимодействие четность не
сохраняет. Проявлялось это в асимметрии вылета бетараспадных электронов по направлению ориентации ядер и
против нее.
Если бы четность сохранялась, вылет бета- электронов
был бы симметричным.
9.
За это открытие вышеперечисленные физики в 1957 годуполучили Нобелевскую премию по физике.
10.
Что является удивительным в этом открытии? Операцияинверсии с заменой r r - это замена декартовых
переменных x, y, z на -x, -y, -z, что эквивалентно замене
правой системы декартовых координат на левую (или
наоборот). Физики привыкли, что физические законы – это
объективная реальность, и они не зависят от того, в какой
системе координат (правой или левой) их описывать.
Результат должен был быть одинаков! Несохранение
четности же означает, что описание явления в правой или
левой системах координат даст различные результаты.
Для явлений с участием слабого взаимодействия это было
подтверждено экспериментально. Физика с такими
явлениями столкнулась впервые. Заметим, что в
классической физике такого интеграла состояния, как
четность, не существует, это квантовое понятие.
11. Проверочные вопросы к лекции 16. 1. Что означает интеграл состояния «четность»? 2. Какое свойство пространства способствует
сохранению четности состояния?3. Каковы собственные значения у оператора инверсии?
4. В чем суть опытов по проверки сохранения четности
при слабом взаимодействии?
12.
Лекция 17МАТРИЧНЫЙ ФОРМАЛИЗМ КВАНТОВОЙ
МЕХАНИКИ – ТЕОРИЯ ПРЕДСТАВЛЕНИЙ
13.
Основы матричного формализма в квантовой механикебыли заложены В.Гейзенбергом еще до того, как стало
известным уравнение Шредингера. По своей сути, это ее
альтернативный вариант, иногда более удобный при
решении некоторых задач. В традиционном формализме
волновая функция Ψ( r, t) и собственные функции
операторов определяются в координатном пространстве.
ˆ Fˆ ( r , )
F
В нем же действуют и физические операторы
r . В
этом случае говорят о координатном представлении.
Однако возможны и другие представления функций и
операторов.
Пусть для некоторого линейного и эрмитового оператора Ĝ
известны собственные функции и собственные значения
(для определенности пусть спектр будет дискретным):
ˆ ( r ) G ( r ), n 1, 2,...
G
n
n n
(17.1)
Набор собственных функций { 1 ( r ), 2 ( r ),..., n ( r ),... } – это
основа для перехода к G-представлению. Оно называется
так по оператору, чьи собственные функции используются.
14.
Пусть волновая функция в координатном представленииизвестна: Ψ Ψ( r) (время t не включаем). Пользуясь
полнотой системы собственных функций оператора Ĝ ,
разложим по ним волновую функцию:
Ψ(
r) =
a nφ(n
n
r) .
(17.2)
Соответственно для коэффициентов разложения имеем
(см. (6.4)):
an =
*
3
φ(
r)Ψ(
r)
d
r .
n
(17.3)
Формулы (17.2) и (17.3) – это основа для перехода из
координатного в G-представление и наоборот. Зная
волновую функцию Ψ( r) , по ф-ле (17.3) можно получить
соответствующий ей набор коэффициентов {a1, a2, …, an,
…}. И, наоборот, получив каким-то образом набор
коэффициентов {a1, a2, …, an, …}, по ф-ле (17.2) можно
найти волновую функцию Ψ( r) . Иными словами, имеет
место взаимно однозначное соответствие: Ψ( r)
{a1, a2,
…, an, …}. Оно позволяет назвать набор коэффициентов
{a1, a2, …, an, …} тоже волновой функцией, но только не в
координатном, а в G-представлении.
15.
Получается, что в G-представлении это не функция, аопределенный набор чисел или матрица из этих чисел
с одним столбцом:
Ψ( r)
a1
a
2
A = ...
.
a
n
...
(17.4)
Пусть теперь оператор Ĝ имеет непрерывный спектр и
известны его собственные функции, т.е. решение
уравнения
ˆ (G , r ) G (G , r ) .
G
(17.5)
Тогда вместо соотношений (17.2) и (17.3) будет
( r ) a (G ) (G, r )dG ;
(17.6)
a (G ) * (G, r ) ( r )d 3r .
(17.7)
Как и в случае дискретного спектра имеет место взаимно
однозначное соответствие волновой функции Ψ( r) и
функции a(G). Поэтому функцию a(G) можно назвать
волновой функцией в G-представлении.
16.
Ограничимся дальше только случаем дискретного спектра уоператора Ĝ . Рассмотрим, какой вид принимает заданный
оператор Fˆ Fˆ ( r , r ) . Пусть его действие определено
соотношением:
ˆ ( r ) ( r ) ,
F
(17.8)
1
2
где от функций 1 ( r ), 2 ( r ) только требуется, чтобы они
удовлетворяли стандартным условиям. Переведем их в Gпредставление.
1 ( r ) an n ( r ) ;
(17.9)
n
2 ( r ) bn n ( r ) .
(17.10)
n
В соответствии с данными выше определениями
совокупности коэффициентов {a1, a2, …, an, …} и {b1, b2, …,
bn, …} – это соответственно функции 1 ( r ) и 2 ( r ) в Gпредставлении. Подставляя разложения (17.9) и (17.10) в
соотношение (17.8), получим его эквивалент в Gпредставлении.
a
n
n
Fˆ n ( r )
b
n
n
n
(r )
.
17.
*Умножим обе части этого соотношения на m ( r ) ,
проинтегрируем по координате и воспользуемся свойством
ортонормировки собственных
функций n ( r ) :
*
3
ˆ
a
(
r
)
F
(
r
)
d
r
n m
n
n
bn m* ( r ) n ( r )d 3r bn mn bm ;
n
bm Fmn an
n
n
.
(17.11)
Здесь, как и n, m = 1, 2, 3, … и введено обозначение
Fmn m* ( r ) Fˆ n ( r )d 3r .
(17.12)
18.
Таким образом, соотношение (17.11) – это не одно, асистема алгебраических уравнений, и она есть эквивалент
соотношения (17.8) в G-представлении. Тогда входящую в
эту систему уравнений матрицу из матричных элементов
Fmn можно назвать оператором F̂ в G-представлении.
Итак, получаем, что оператор F̂ в G-представлении имеет
вид матрицы:
Fˆ
F Fmn
F11
F
21
...
Fn1
...
F12
...
F1n
F22
... F2 n
...
...
...
Fn 2
...
Fnn
...
...
...
...
...
...
... .
...
(17.13)
Заметим, что систему уравнений (17.11) можно сразу
записать в матричном виде:
B = F A .
Здесь (·) – символ матричного умножения, матрицы A и B –
это функции
1 ( r ) и 2 ( r ) в G-представлении, имеющие
вид
19.
a1a
2
A = ... ; B =
an
...
b1
b
2
...
,
bn
...
а матрица F была определена выше.
Посмотрим, как должен выглядеть оператор в своем
собственном представлении, т.е. когда оператор Ĝ - это
ˆ F
ˆ . Тогда функции
и есть оператор F̂ : G
1 ( r ), 2 ( r ),..., n ( r ),... - это собственные функции
оператора F̂ :
ˆ (r ) F ( r ), n 1, 2,...
F
n
n n
(17.14)
Для матричных элементов Fmn в соответствии (17.12)
получим:
Fmn m* ( r ) Fˆ n ( r )d 3r
Fn m* ( r ) n ( r )d 3r Fn mn .
20.
Здесь использованы условие ортонормировки собственныхфункций и для подчеркнутого выражения соотношение
(17.14). Таким образом, в своем собственном
представлении оператор представляется диагональной
матрицей и по диагонали стоят его собственные
значения:
Fˆ
F Fn mn
F1
0
...
0
...
0
...
0
F2
...
0
...
...
...
0
...
Fn
...
...
...
...
...
...
... .
...
(17.15)
Приведем еще часто используемый в матричном виде
оператор F̂
Fˆ * , который называется оператором,
сопряженным оператору F̂ , и часто используется на
практике. В приведенном определении тильда означает
транспонирование матрицы, т.е. замену строк на столбцы и
наоборот, звездочка – операцию комплексного сопряжения.
21.
Fˆ Fˆ *F11*
*
F12
...
*
F1n
...
*
F F * Fnm
*
F21
...
Fn*1
*
F22
...
Fn*2
...
...
...
F2*n
...
*
Fnn
...
...
...
...
...
...
...
...
.
Можно показать, что для эрмитово сопряженных
операторов
F11*
*
F12
...
*
F1n
...
*
F21
...
Fn*1
*
F22
...
Fn*2
...
...
...
F2*n
...
*
Fnn
...
...
...
Fˆ Fˆ , т.е.
... F11
... F21
... ...
... Fn1
...
...
F12
...
F1n
F22
...
F2 n
...
...
...
Fn 2
...
Fnn
...
...
...
*
Fmn Fnm
...
...
...
... ,
...
или
(m, n = 1, 2, 3, …).
Пользуясь волновой функцией в G-представлении, можно
рассчитать непосредственно в этом представлении
среднее значение физической величины F :
22.
F * ( r ) Fˆ ( r )d 3r F A F Aa1*
a2*
F11 F12 ... a1
... F21 F22 ... a2
...
...
...
...
am* Fmn an
m
.
n
Таким образом, для вычисления среднего значения
физической величины нет необходимости возвращаться из
G-представления в координатное, можно сразу
воспользоваться формулой
F am* Fmn an .
m
n
(17.16)
Можно непосредственно в G-представлении найти
собственные значения и собственные функции
F̂ , т.е. эквивалент уравнения
Fˆ ( r ) F ( r ) .
(17.17)
заданного оператора
23.
В G-представлении аналогичное уравнение будет иметьвид:
(F
mn
F mn )cn 0; m 1, 2,...
n
.
(17.18)
Здесь матричные элементы Fmn определены ф-лой (17.12),
cn - коэффициенты разложения искомой функции по
базисным функциям, т.е. по собственным функциям
оператора Ĝ :
( r ) cn n (r ) . Их совокупность {c , c , …}
1
2
n
для каждого собственного значения F будет определять
искомую собственную функцию оператора F̂ в Gпредставлении.
Система уравнений (17.18) однородная. Как известно, для
нахождения ее нетривиального решения (тривиальное –
это все cn = 0) следует приравнять нулю определитель
матрицы Fmn F mn :
det Fmn F mn 0 ,
24.
F11или в явном виде
F
F12
F13
...
F21
F22 F
F23
...
F31
F32
F33 F
...
0
.
...
...
...
...
Если определитель раскрыть, получится алгебраическое
уравнение по степеням искомой величины F, решение
которого даст его корни F1, F2, …, Fk, … Подставляя k-ый
корень Fk в систему уравнений (17.18) и решая ее, найдем
(k )
(k )
c
,
c
соответствующий набор коэффициентов 1
2 , , т.е.
собственную функцию k ( r ) оператора F̂ в Gпредставлении. И так для каждого Fk (k = 1, 2, …), получив
тем самым все соответствующие собственные функции в
G-представлении.
Точно также непосредственно в G-представлении можно
решить уравнение Шрёдингера для стационарных
состояний, получить спектр энергий и соответствующие
волновые функции. Вид уравнения Шрёдингера
ˆ ( r ) E ( r ) в G-представлении будет аналогичен
H
алгебраической системе уравнений (17.18):
(H
n
mn
E mn )an 0; m 1, 2,...
(17.19).
25.
Здесь набор коэффициентов {a1, a2, …} – волновая функциястационарного состояния Ψ( r) в G-представлении и
H mn
*
ˆ ( r ) d 3r
(
r
)
H
n
m
(17.20)
- гамильтониан в G-представлении. Дальнейшие действия
для нахождения энергетического спектра E1, E2,…, Ek,… и
(k )
(k )
a
,
a
соответствующих волновых функций { 1
2 , } (k = 1,
2,…) из системы уравнений (17.19) такие же, как и при
решении системы уравнений (17.18).
Наконец, можно получить в G-представлении аналог
временного уравнения Шрёдингера
i
( r , t )
ˆ ( r , t ) ( r , t )
H
;
t
Hˆ ( r , t ) -
2
2m
(17.21)
2 U ( r , t ) .
Перейдем в G-представлении, разложив волновую
функцию ( r , t ) по базисным функциям n ( r )
(n = 1, 2, …):
( r , t ) an (t ) n ( r ) .
n
(17.22)
26.
Подставляя (17.22) в (17.21) получим:dan (t )
n ( r , t ) an (t ) Hˆ ( r , t ) n ( r ) .
dt
n
n
*
Умножим это равенство m ( r ) (m = 1, 2, …) и
проинтегрируем по r .
da (t )
i n m* ( r ) n ( r )d 3r
dt
n
a (t ) * ( r ) Hˆ ( r , t ) ( r )d 3r ;
i
n
n
m
n
dam (t )
i
H mn (t )an (t ) , m = 1, 2, …
dt
n
(17.23)
При получении (17.23) использовано условие
ортонормировки для базисных функций n ( r ) и введено
обозначение:
ˆ ( r , t ) ( r )d 3r
H mn (t ) m* ( r ) H
n
.
27.
Это есть система дифференциальных уравненийпервого порядка по времени. Ее решение позволяет найти
совокупность величин a1(t), a2(t), …, an(t), …, т.е. волновую
функцию в G-представлении. Однако для определенности
решения необходимо к системе дифференциальных
уравнений (17.23) задать начальные условия an(t=0) (n =
1, 2, …).
Суммируем все сказанное в виде таблицы.
Ψ(
ˆ ( r ) G ( r ), n 1, 2,...
G
n
n
n
r) = a nφ(n r)
a n = φ(*n r)Ψ( r) d 3r
n
Координатное
представление
G-представление
Ψ( r)
{a1, a2, …, an, …}
F11
F21
...
F Fmn
ˆ F
ˆ ( r , r )
F
ˆ (r ) F (r )
F
F
(F
mn
n
ˆ ( r ) E ( r )
H
i
( r , t )
ˆ ( r , t ) ( r , t )
H
t
ˆ (r , t ) H
2
2m
2 U ( r , t )
(H
F22
...
...
...
;
...
( r ) Fˆ ( r )d r
a F a
Fmn
ˆ ( r )d 3r
F * ( r ) F
F12
*
m
3
n
*
m
m
mn
n
n
F mn )cn 0; m 1, 2,...
mn
E mn )an 0; m 1, 2,... ;
n
H mn
i
*
m
dam (t )
dt
ˆ ( r ) d 3r
(r ) H
n
H
mn
( t ) an ( t ) , m =
n
1, 2, …;
*
ˆ ( r , t ) ( r )d 3r
H mn (t ) m
(r ) H
n

























 Физика
Физика








