Похожие презентации:
Пирамида. Элементы пирамид
1.
2. Содержание
1)2)
3)
4)
5)
6)
7)
8)
9)
Понятие и чертёж
История развития пирамиды в геометрии
Элементы пирамиды
Виды пирамиды
Правильная пирамида
Свойства правильной пирамиды
Усечённая пирамида
Свойства усечённой пирамиды
Пирамиды вокруг нас
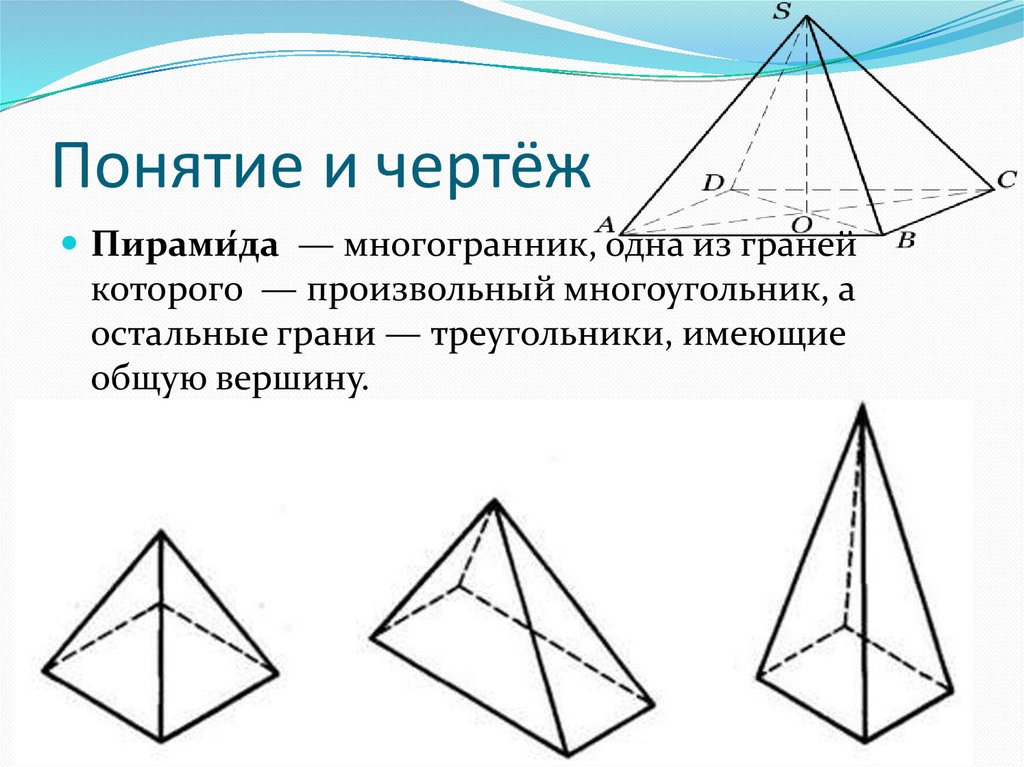
3. Понятие и чертёж
Пирами́да — многогранник, одна из гранейкоторого — произвольный многоугольник, а
остальные грани — треугольники, имеющие
общую вершину.
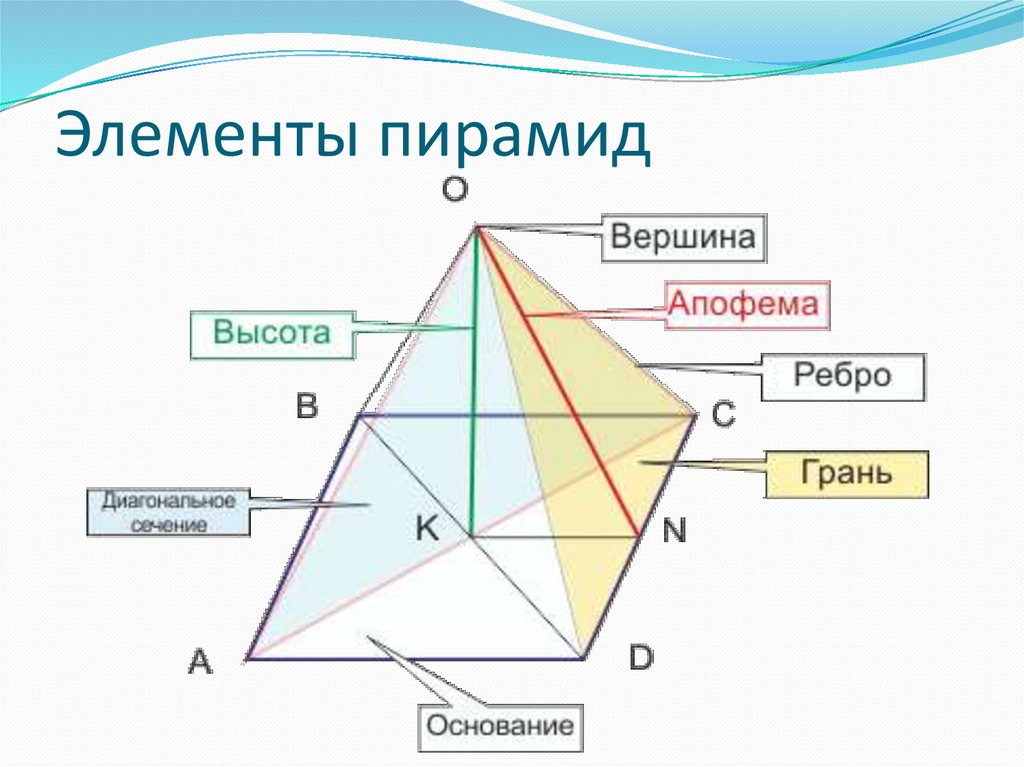
4. Элементы пирамид
5.
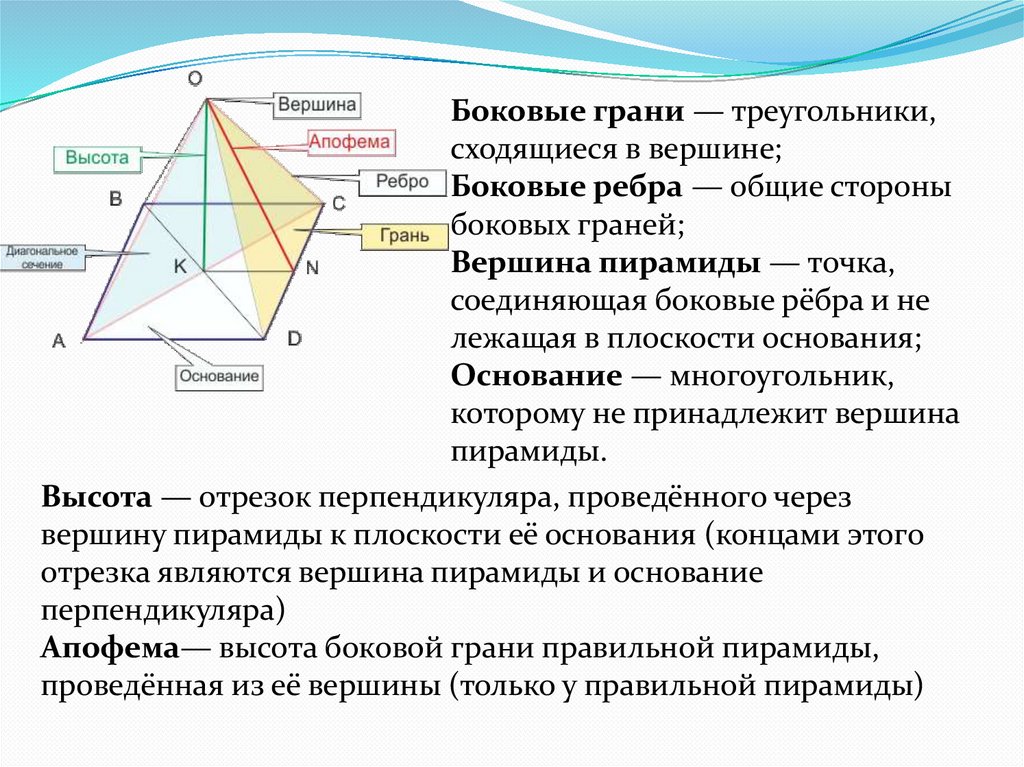
Боковые грани — треугольники,сходящиеся в вершине;
Боковые ребра — общие стороны
боковых граней;
Вершина пирамиды — точка,
соединяющая боковые рёбра и не
лежащая в плоскости основания;
Основание — многоугольник,
которому не принадлежит вершина
пирамиды.
Высота — отрезок перпендикуляра, проведённого через
вершину пирамиды к плоскости её основания (концами этого
отрезка являются вершина пирамиды и основание
перпендикуляра)
Апофема— высота боковой грани правильной пирамиды,
проведённая из её вершины (только у правильной пирамиды)
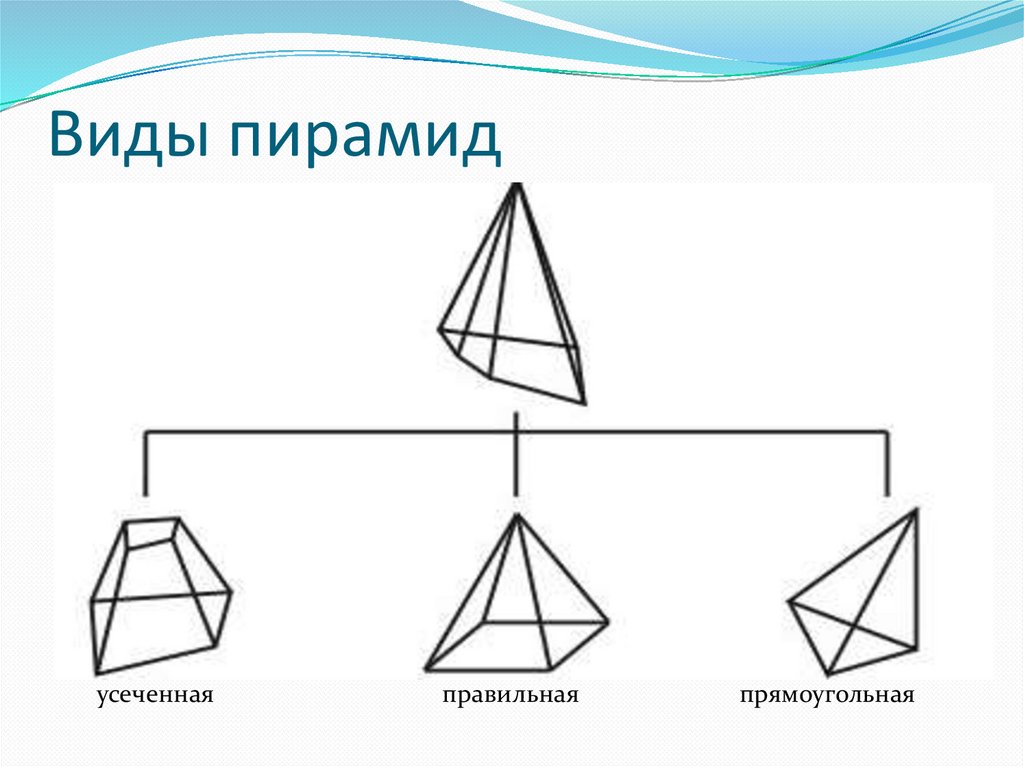
6. Виды пирамид
усеченнаяправильная
прямоугольная
7.
8.
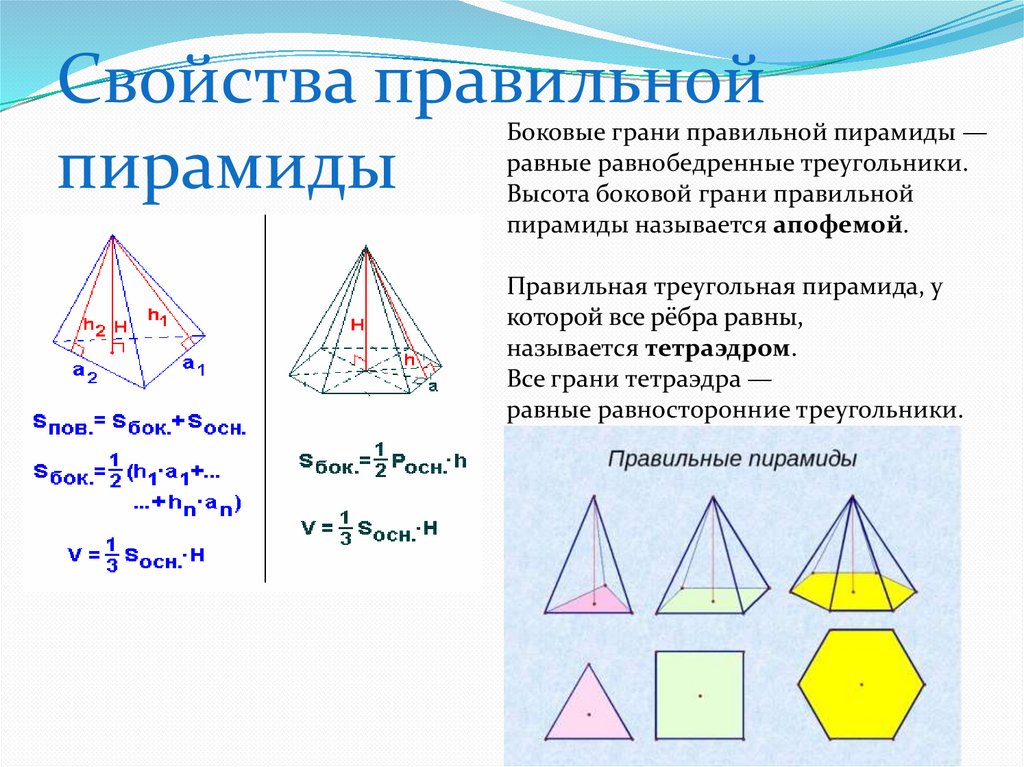
Свойства правильнойпирамиды
Боковые грани правильной пирамиды —
равные равнобедренные треугольники.
Высота боковой грани правильной
пирамиды называется апофемой.
Правильная треугольная пирамида, у
которой все рёбра равны,
называется тетраэдром.
Все грани тетраэдра —
равные равносторонние треугольники.
9. Свойства правильных пирамид
Боковые грани правильной пирамиды - равные другдругу равнобедренные треугольники.
Если все боковые ребра равны, то высота
проектируется в центр описанной окружности;
Боковые ребра образуют с плоскостью основания
равные углы.
Если боковые грани наклонены к плоскости основания
под одним углом, то высота проектируется в центр
вписанной окружности;
Высоты боковых граней равны;
Площадь боковой поверхности равна половине
произведения периметра основания на высоту боковой
грани
Боковые ребра правильной пирамиды - равны.
10. Усеченная пирамида
Плоскость, параллельная плоскости основания пирамиды ипересекающая пирамиду, отсекает от нее подобную пирамиду. Другая
часть пирамиды представляет собой многогранник, который
называют усеченной пирамидой.
На рисунке изображена усеченная
пирамида ABCDA1B1C1D1. Грани усеченной
пирамиды, лежащие в параллельных
плоскостях (ABC) и (B1C1D1),
называют основаниями усеченной
пирамиды, остальные грани
называют боковыми гранями.
Основания усеченной пирамиды
представляют собой подобные
многоугольники, боковые грани трапеции. Усеченную пирамиду, которая
получается из правильной пирамиды,
также называют правильной.
11. Свойства усеченной пирамиды:
Основания усеченной пирамиды — подобныемногоугольники.
Боковые грани усеченной пирамиды — трапеции.
Боковые ребра правильной усеченной пирамиды
равны и одинаково наклонены к основанию пирамиды.
Боковые грани правильной усеченной пирамиды —
равные между собой равнобедренные трапеции и
одинаково наклонены к основанию пирамиды.
Двугранные углы при боковых ребрах правильной
усеченной пирамиды равны.
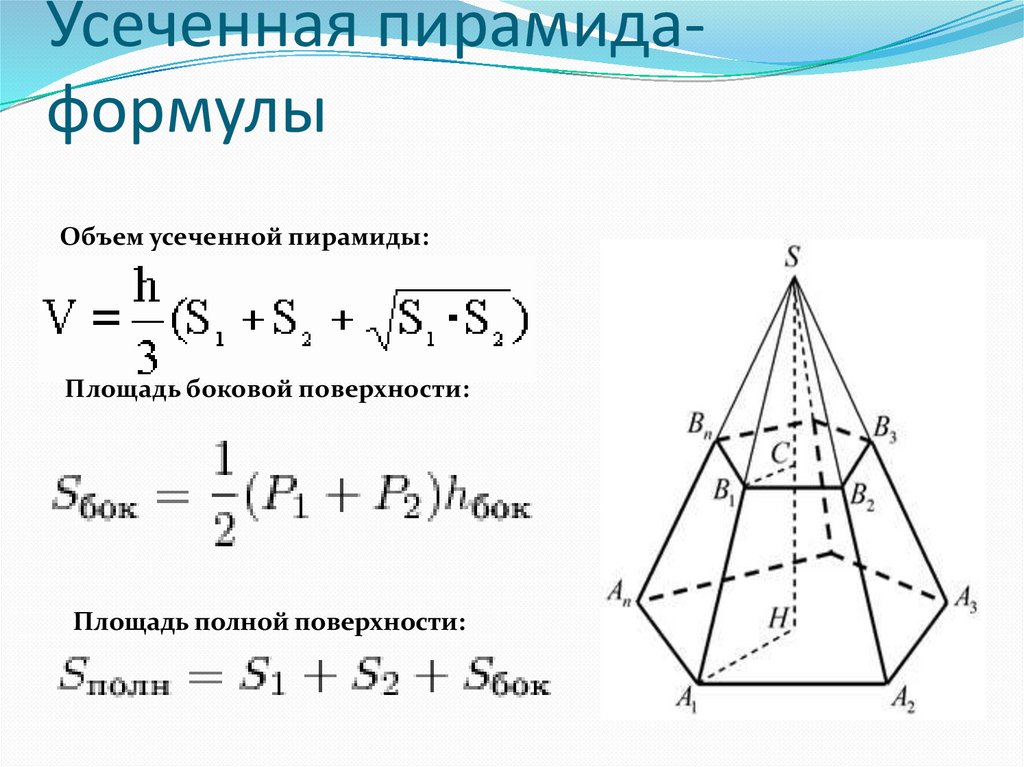
12. Усеченная пирамида- формулы
Усеченная пирамидаформулыОбъем усеченной пирамиды:
Площадь боковой поверхности:
Площадь полной поверхности:







 Математика
Математика








