Пирамида. Правильная пирамида. Усечённая пирамида

1. ПИРАМИДА. Правильная пирамида. Усечённая пирамида.

2.

Слово «пирамида» — греческое.
По мнению одних исследователей,
большая куча пшеницы
и стала прообразом
пирамиды.
По мнению других учёных,
это слово произошло
от названия
поминального пирога
пирамидальной формы.

3.

4. Современные пирамиды

• Самая большая пирамида,
высотой 44 метра,
расположена в Московской
области.

5.

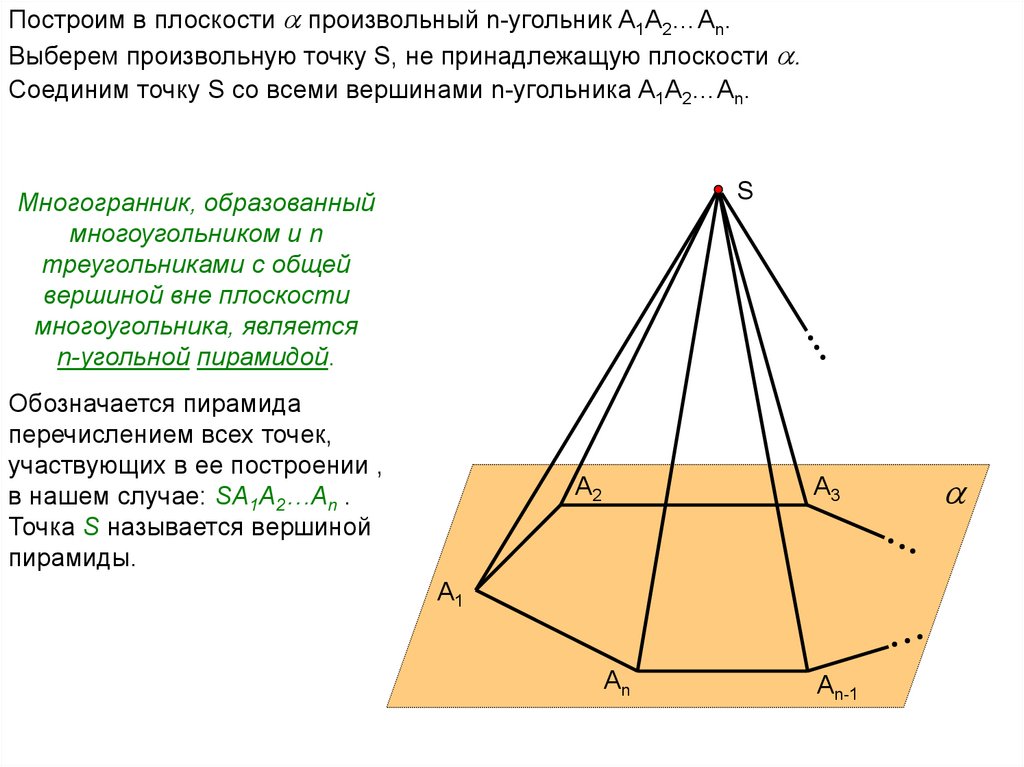
Построим в плоскости произвольный n-угольник A1A2…An.
Выберем произвольную точку S, не принадлежащую плоскости .
Соединим точку S со всеми вершинами n-угольника A1A2…An.
S
Многогранник, образованный
многоугольником и n
треугольниками с общей
вершиной вне плоскости
многоугольника, является
n-угольной пирамидой.
Обозначается пирамида
перечислением всех точек,
участвующих в ее построении ,
в нашем случае: SA1A2…An .
Точка S называется вершиной
пирамиды.
A2
A3
A1
An
An-1

6.

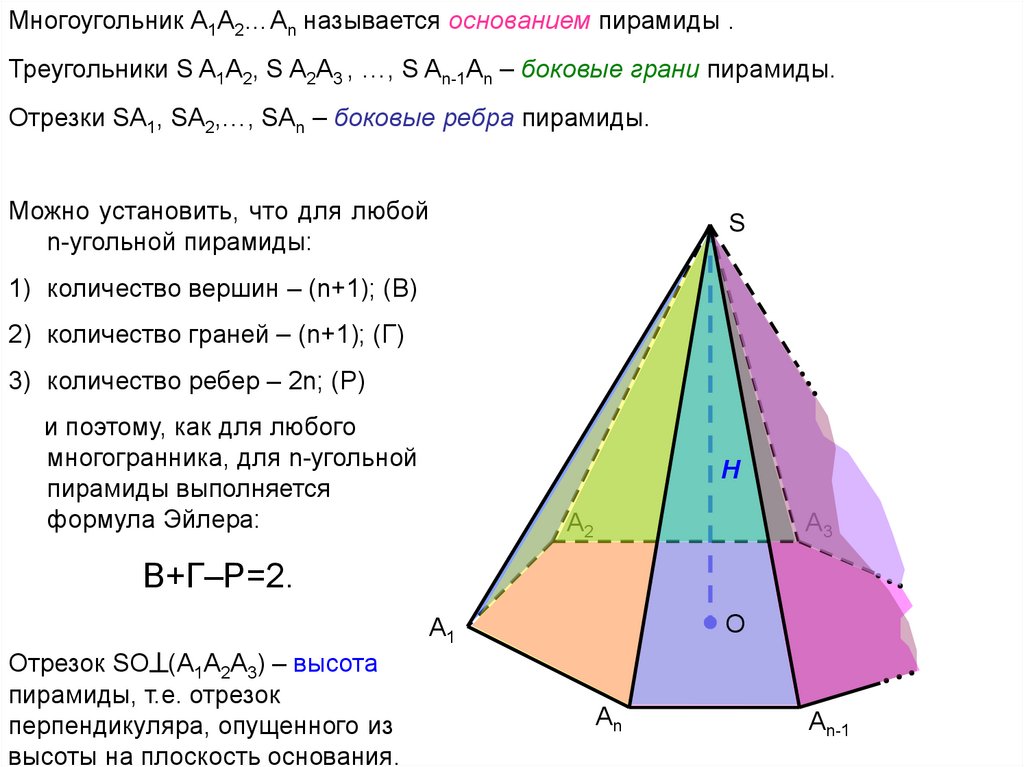
Многоугольник A1A2…An называется основанием пирамиды .
Треугольники S A1A2, S A2A3 , …, S An-1An – боковые грани пирамиды.
Отрезки SA1, SA2,…, SAn – боковые ребра пирамиды.
Можно установить, что для любой
n-угольной пирамиды:
S
1) количество вершин – (n+1); (В)
2) количество граней – (n+1); (Г)
3) количество ребер – 2n; (Р)
и поэтому, как для любого
многогранника, для n-угольной
пирамиды выполняется
формула Эйлера:
H
A2
A3
В+Г–Р=2.
Отрезок SO (A1A2A3) – высота
пирамиды, т.е. отрезок
перпендикуляра, опущенного из
высоты на плоскость основания.
O
A1
An
An-1

7.

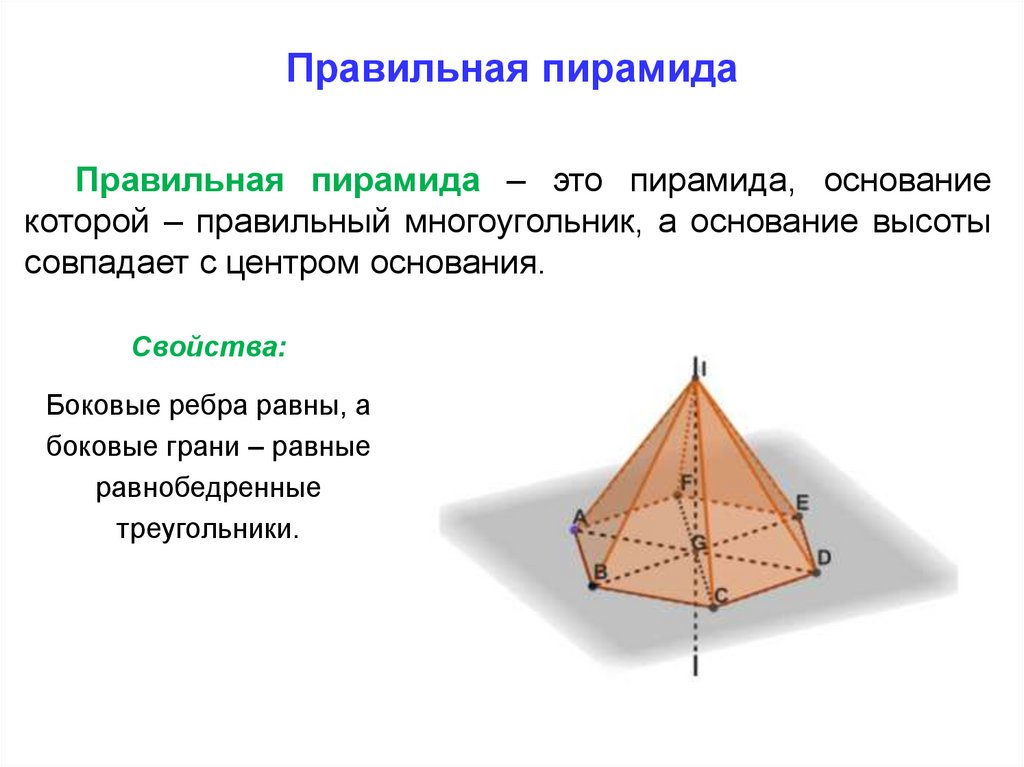
Правильная пирамида
Правильная пирамида – это пирамида, основание
которой – правильный многоугольник, а основание высоты
совпадает с центром основания.
Свойства:
Боковые ребра равны, а
боковые грани – равные
равнобедренные
треугольники.

8.

• Осью правильной пирамиды
называется прямая, содержащая её
высоту.
Ось
пирамиды

9.

• Высота боковой грани правильной
пирамиды, проведённая из её
вершины, называется апофемой.
• SF – апофема пирамиды SABCD.
S
Апофема
пирамиды
B
С
F
A
D

10.

l

11.

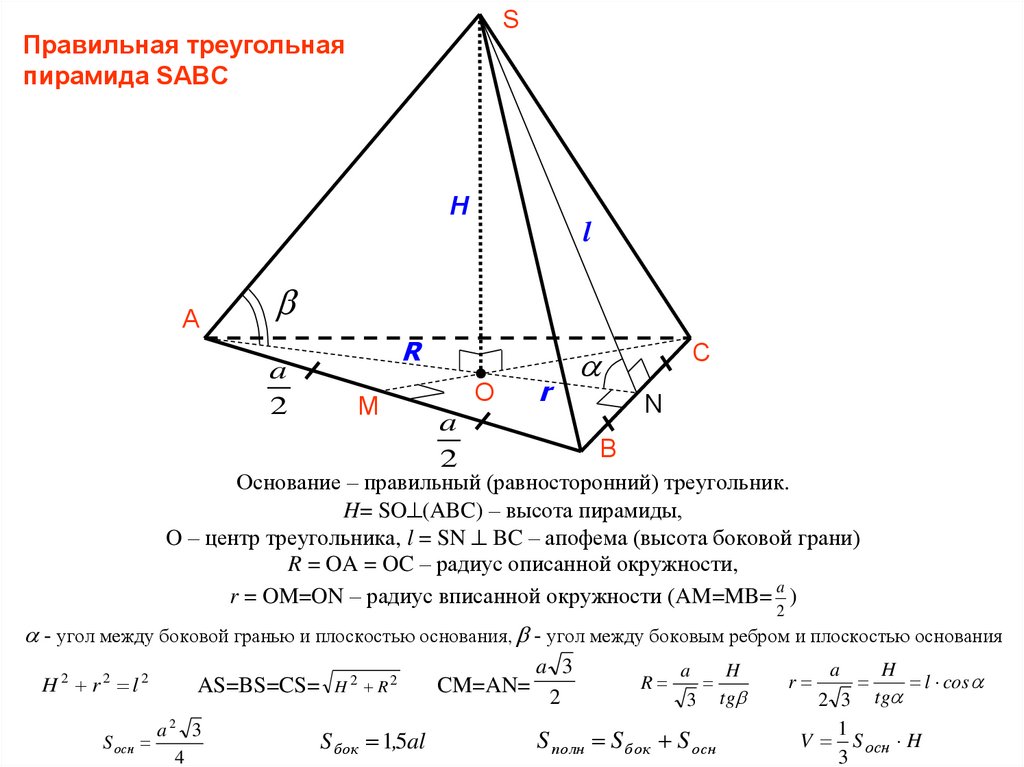
S
Правильная треугольная
пирамида SABC
H
l
A
a
2
R
M
O
r
a
2
C
N
B
Основание – правильный (равносторонний) треугольник.
H= SO (ABC) – высота пирамиды,
O – центр треугольника, l = SN BC – апофема (высота боковой грани)
R = OA = OC – радиус описанной окружности,
r = OM=ON – радиус вписанной окружности (AM=MB= a )
2
- угол между боковой гранью и плоскостью основания, - угол между боковым ребром и плоскостью основания
H 2 r2 l2
AS=BS=CS= H 2 R 2
a2 3
S осн
4
S бок 1,5al
CM=AN=
a 3
2
R
a
3
S полн S бок S осн
H
tg
r
a
H
l cos
tg
2 3
1
V S осн H
3

12.

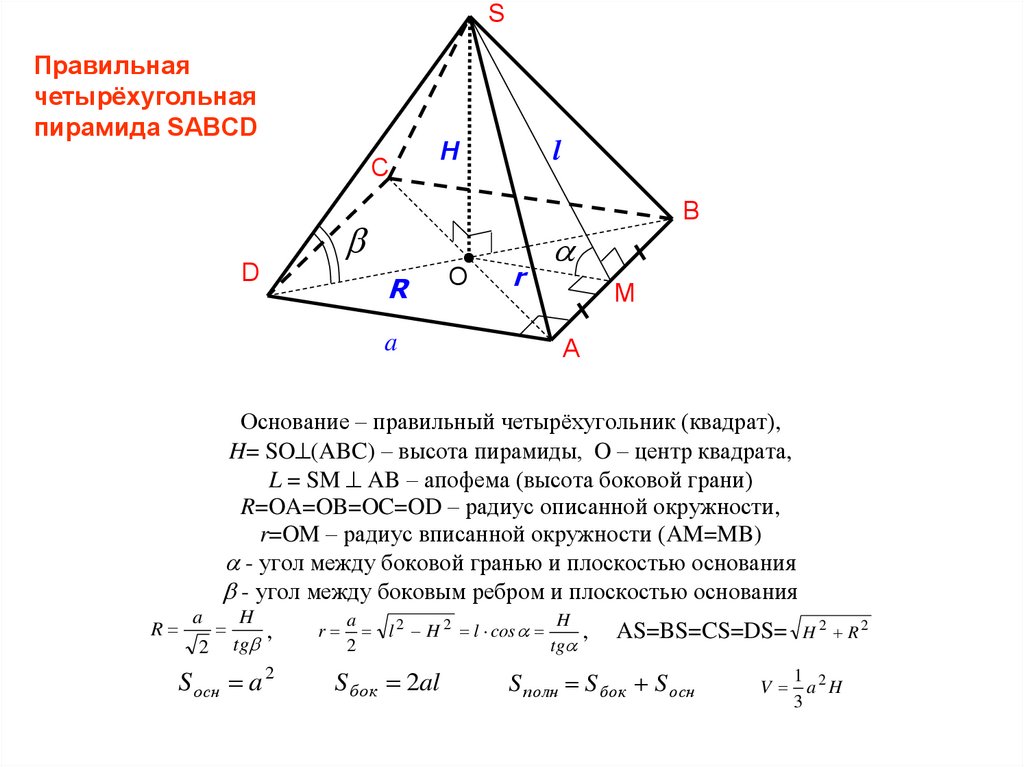
S
Правильная
четырёхугольная
пирамида SABCD
C
В
D
l
H
R
a
O
r
M
A
Основание – правильный четырёхугольник (квадрат),
H= SO (ABC) – высота пирамиды, O – центр квадрата,
L = SM AB – апофема (высота боковой грани)
R=OA=OB=OC=OD – радиус описанной окружности,
r=OM – радиус вписанной окружности (AM=MB)
- угол между боковой гранью и плоскостью основания
- угол между боковым ребром и плоскостью основания
R
a
2
H
,
tg
S осн a 2
r
a
H
l 2 H 2 l cos
,
2
tg
S бок 2al
AS=BS=CS=DS= H 2 R 2
S полн S бок S осн
V
1 2
a H
3

13.

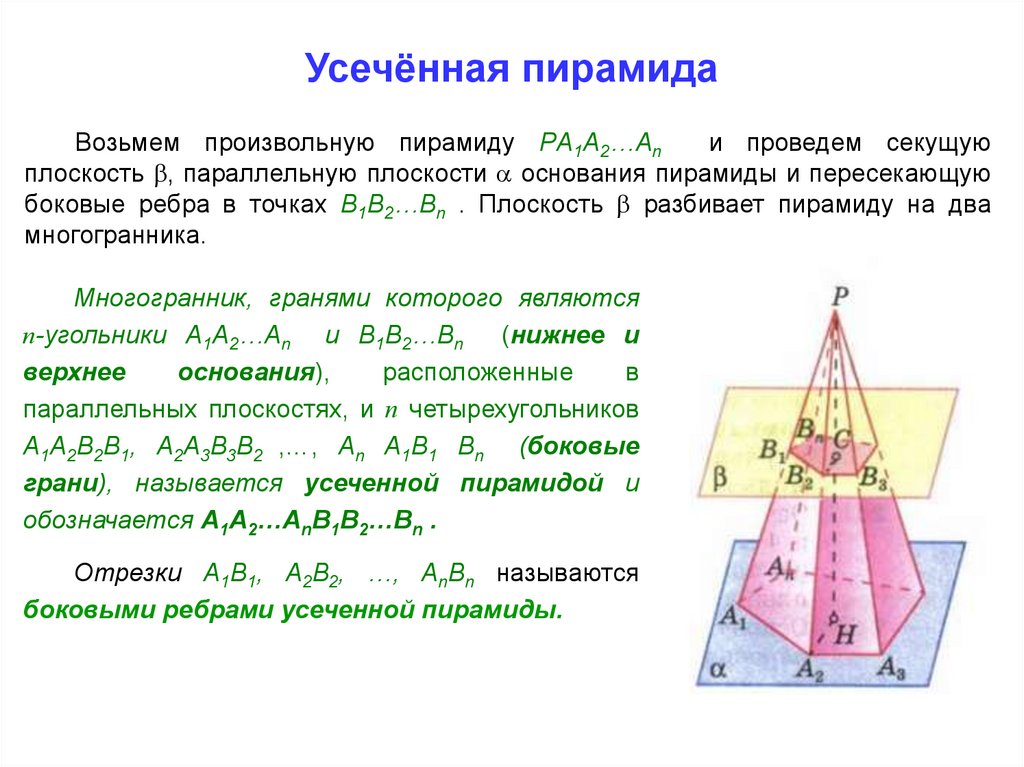
Усечённая пирамида
Возьмем произвольную пирамиду РA1A2…An
и проведем секущую
плоскость , параллельную плоскости основания пирамиды и пересекающую
боковые ребра в точках В1В2…Вn . Плоскость разбивает пирамиду на два
многогранника.
Многогранник, гранями которого являются
п-угольники A1A2…An и В1В2…Вn (нижнее и
верхнее
основания),
расположенные
в
параллельных плоскостях, и п четырехугольников
A1A2В2В1, А2A3В3В2 ,…, An A1В1 Вn (боковые
грани), называется усеченной пирамидой и
обозначается A1A2…AnВ1В2…Вn .
Отрезки A1В1, A2В2, …, AnВn называются
боковыми ребрами усеченной пирамиды.

14.

Усечённая пирамида
Перпендикуляр, проведенный из какой-нибудь точки одного основания к
плоскости другого основания, называется высотой усеченной пирамиды.
Усеченная пирамида называется правильной, если она получена
сечением правильной пирамиды плоскостью, параллельной основанию.
Свойства:
1) Основания
(правильной)
многоугольники.
усеченной
пирамиды
2) Боковые грани усеченной пирамиды – трапеции.
Боковые грани правильной усеченной пирамиды –
равнобедренные трапеции. Высоты этих трапеций
называются апофемами.
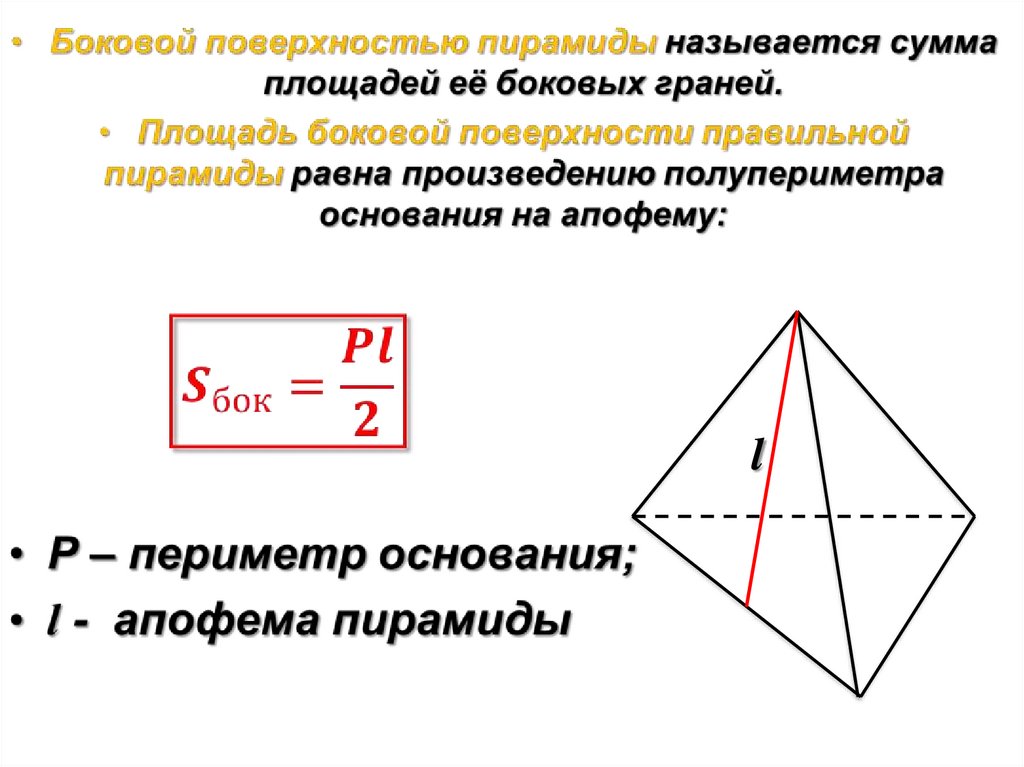
Площадью
боковой
поверхности
усеченной
пирамиды называется сумма площадей ее боковых
граней.
Теорема. Площадь боковой поверхности правильной
усеченной пирамиды равно произведению полусуммы
периметров оснований (p1 и p2) на апофему l :
–
(правильные)

15.

1. В основании пирамиды Хеопса – квадрат со стороной 230м,
тангенс угла наклона боковой грани к основанию равен 1,2.
Найти высоту самой высокой египетской пирамиды, если
основание ее лежит в центре квадрата.
Решение:
S
1. AC ВD = О
2. Пирамида правильная
SО (АВС)
В
А
С
4. SЕ СD (по теореме о 3-х
О
E
D
7. SО = ОЕ • tg E = 115 • 1,2 = 138 м
Ответ: 138 м.
3. ОЕ АD ОЕ СD
перпендикулярах)
5. SОЕ – п\у tg E = SО : ОЕ
6. ОЕ = 0,5АD =115м

16.

2. В основании пирамиды Хеопса – квадрат со стороной 230м,
высота пирамиды 138 м. Найти боковое ребро самой высокой
египетской пирамиды.
Решение:
1. AC ВD = О
S
2. АОD – п\у, р\б
по т. Пифагора
В
АD2 = DО2+ОА2
2ОD2= 2302 = 52900
2
А
С ОD = 26450
3. Пирамида правильная
О
SО (АВС)
230 м
4. SОD – п\у
D
по т. Пифагора DS2 = DО2+ОS2 = 26450 + 1382=
= 26450 +19044 = 45494
DS 213 м
Ответ: 213 м.

17.

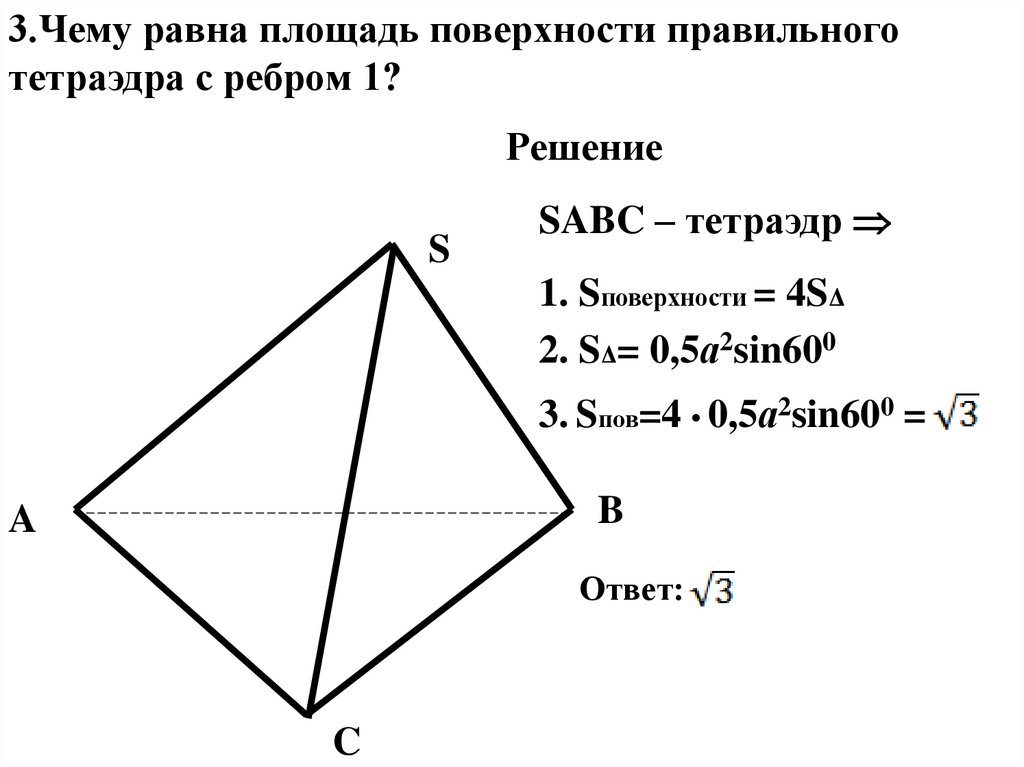
3.Чему равна площадь поверхности правильного
тетраэдра с ребром 1?
Решение
S
SABC – тетраэдр
1. Sповерхности = 4SΔ
2. SΔ= 0,5а2sin600
3. Sпов=4 • 0,5а2sin600 =
B
A
Ответ:
C

18.

4. Найдите площадь боковой поверхности пирамиды
Хеопса, сторона основания которой равна 230 м и
высота 138 м.
Решение:
S
В
А
С
О
E
D
1. Sб.пов=4Sтр
2. AC ВD = О
3. Пирамида правильная
SО (АВС)
4. ОЕ СD ОЕ АD
5. SЕ АD (по теореме о 3
перпендикулярах)
6. SОЕ – п\у
по т. Пифагора
ЕS2 = ЕО2+ОS2 = 1152 + 1382 =
= 13225 +19044 = 32269
ЕS 180
7. ES - высота АSD
SАSD = 0,5 ЕS•АD = 0,5 •180 • 230 =20700 м2
8. Sб.пов=4Sтр = 4 • 20700 = 82800 м2
Ответ: 82800 м2

19.

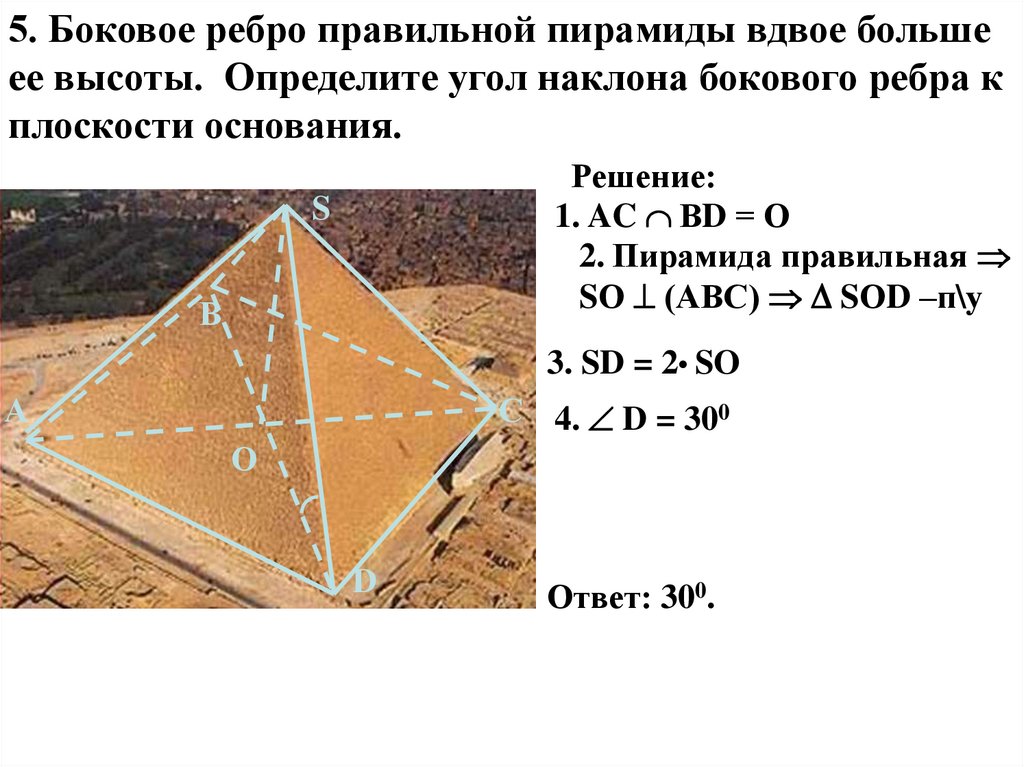
5. Боковое ребро правильной пирамиды вдвое больше
ее высоты. Определите угол наклона бокового ребра к
плоскости основания.
Решение:
1. AC ВD = О
2. Пирамида правильная
SО (АВС) SОD –п\у
S
В
3. SD = 2• SO
А
С 4. D = 300
О
D
Ответ: 300.