Инвестиции и их оценка

1. ИНВЕСТИЦИИ И ИХ ОЦЕНКА

2. ОСНОВНЫЕ КРИТЕРИИ ЭФФЕКТИВНОСТИ ИНВЕСТИЦИОННЫХ ПРОЕКТОВ

Чистая текущая стоимость (NPV)
Внутренняя норма рентабельности (IRR)
Модифицированная
внутренняя норма
рентабельности (MIRR)
Индексы рентабельности (PI)
Простой
(недисконтированный)
срок
окупаемости
Дисконтированный срок окупаемости

3. ЧИСТАЯ ТЕКУЩАЯ СТОИМОСТЬ

Чистая текущая стоимость (Net Present Value - NPV) – это разность
между суммой дисконтированных потоков доходов от проекта и
суммой дисконтированных потоков расходов.
Так как в качестве ставки дисконтирования выступает требуемая
инвестором норма дохода на инвестиции в рамках данного
инвестиционного проекта, то экономический смысл NPV –
избыточный (сверх требуемой нормы) доход от проекта в текущих
ценах. Таким образом, чем выше NPV, тем выше «запас прочности»
проекта, выше вероятность того, что требуемая норма дохода может
быть получена инвестором даже в случае менее благоприятных
условий его осуществления, чем то было запланировано.
Проект приемлем только в том случае, если NPV положительна.
Отрицательное значение показателя говорит о том, что доходы на
уровне желаемой инвестором нормы не могут быть получены.
Следовательно, в этом случае реализация проекта экономически
нецелесообразна.
Чем выше ставка дисконтирования, тем ниже NPV.

4. РАСЧЕТ ЧИСТОЙ ТЕКУЩЕЙ СТОИМОСТИ

Рассмотрим следующий проект, рассчитанный на 4 года.
Требуемая инвестором норма дохода на инвестиции – 25%
годовых.
Требуемые первоначальные инвестиции – 120 млн. руб.
Доходы и расходы последующих лет (в млн.руб.):
Годы
1-ый
2-ой
3-ий
4-ый
Доходы
0
20
160
230
Расходы
50
30
10
0

5. РАСЧЕТ ЧИСТОЙ ТЕКУЩЕЙ СТОИМОСТИ

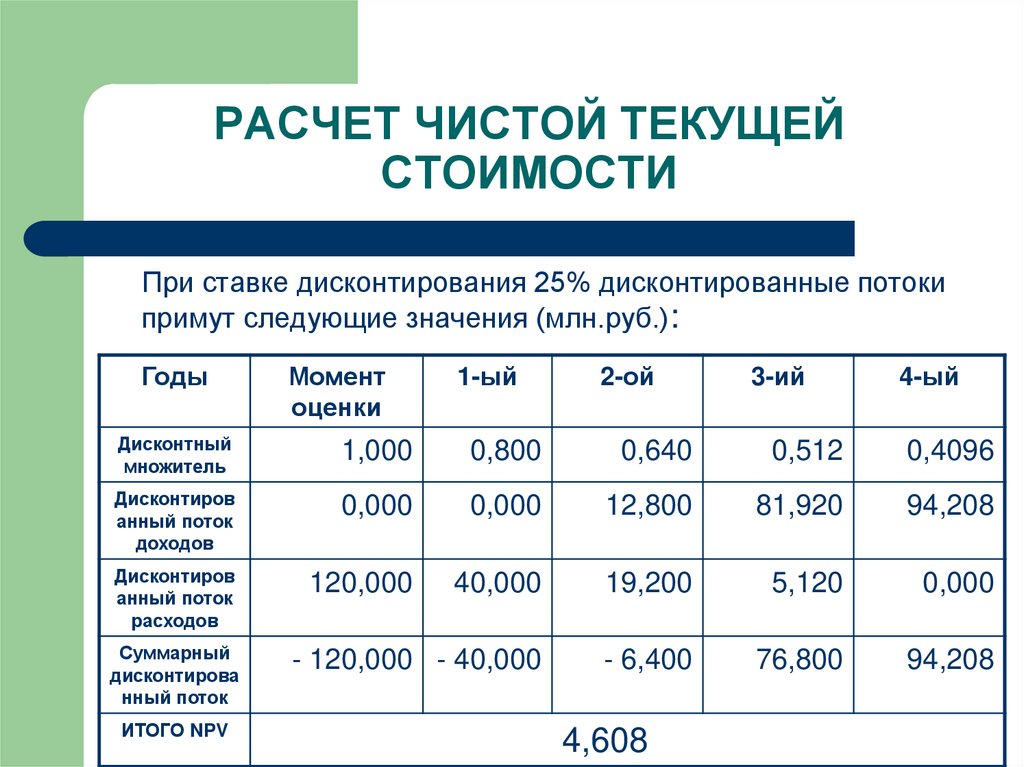
При ставке дисконтирования 25% дисконтированные потоки
примут следующие значения (млн.руб.):
Годы
Момент
оценки
1-ый
2-ой
3-ий
4-ый
Дисконтный
множитель
1,000
0,800
0,640
0,512
0,4096
Дисконтиров
анный поток
доходов
0,000
0,000
12,800
81,920
94,208
Дисконтиров
анный поток
расходов
120,000
40,000
19,200
5,120
0,000
- 120,000 - 40,000
- 6,400
76,800
94,208
Суммарный
дисконтирова
нный поток
ИТОГО NPV
4,608

6. РАСЧЕТ ЧИСТОЙ ТЕКУЩЕЙ СТОИМОСТИ

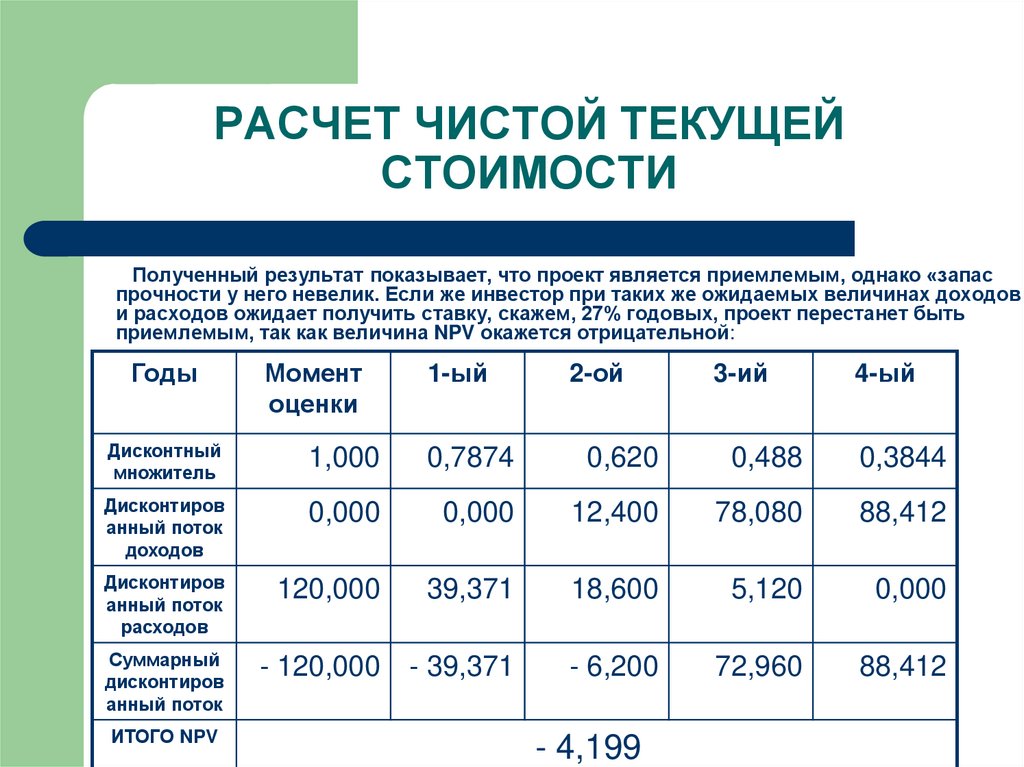
Полученный результат показывает, что проект является приемлемым, однако «запас
прочности у него невелик. Если же инвестор при таких же ожидаемых величинах доходов
и расходов ожидает получить ставку, скажем, 27% годовых, проект перестанет быть
приемлемым, так как величина NPV окажется отрицательной:
Годы
Момент
оценки
1-ый
2-ой
3-ий
4-ый
Дисконтный
множитель
1,000
0,7874
0,620
0,488
0,3844
Дисконтиров
анный поток
доходов
0,000
0,000
12,400
78,080
88,412
Дисконтиров
анный поток
расходов
120,000
39,371
18,600
5,120
0,000
Суммарный
дисконтиров
анный поток
- 120,000
- 39,371
- 6,200
72,960
88,412
ИТОГО NPV
- 4,199

7. Внутренняя норма рентабельности проекта

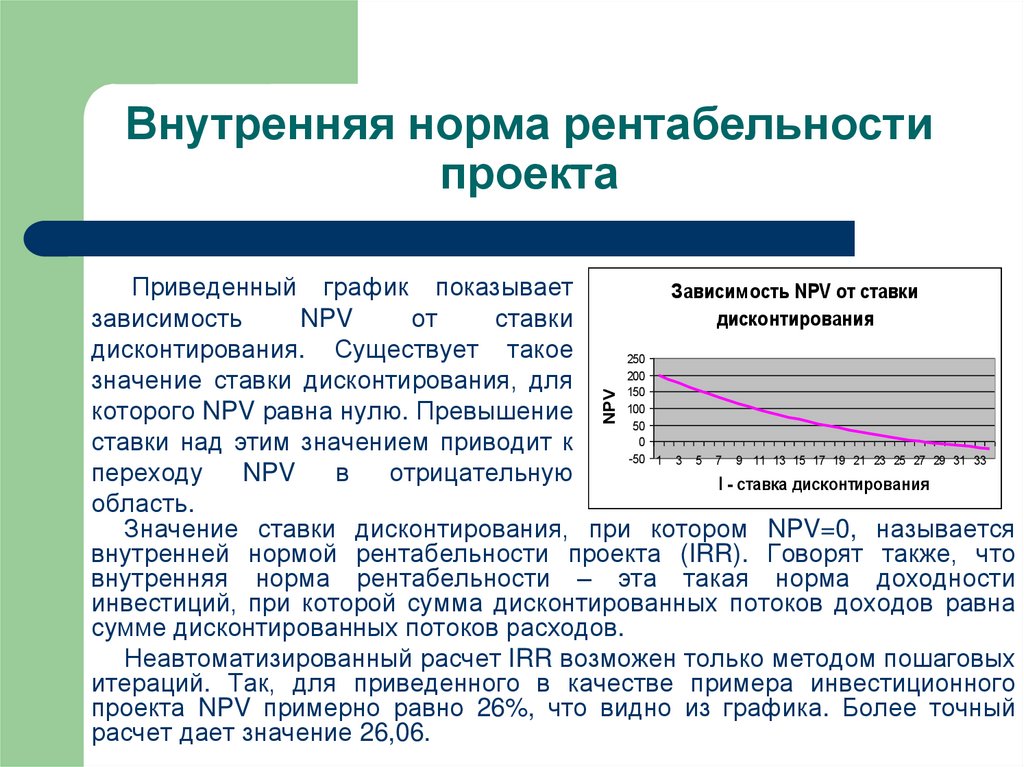
NPV
Приведенный график показывает
Зависимость NPV от ставки
дисконтирования
зависимость
NPV
от
ставки
дисконтирования. Существует такое
250
200
значение ставки дисконтирования, для
150
100
которого NPV равна нулю. Превышение
50
0
ставки над этим значением приводит к
-50 1 3 5 7 9 11 13 15 17 19 21 23 25 27 29 31 33
переходу
NPV
в
отрицательную
I - ставка дисконтирования
область.
Значение ставки дисконтирования, при котором NPV=0, называется
внутренней нормой рентабельности проекта (IRR). Говорят также, что
внутренняя норма рентабельности – эта такая норма доходности
инвестиций, при которой сумма дисконтированных потоков доходов равна
сумме дисконтированных потоков расходов.
Неавтоматизированный расчет IRR возможен только методом пошаговых
итераций. Так, для приведенного в качестве примера инвестиционного
проекта NPV примерно равно 26%, что видно из графика. Более точный
расчет дает значение 26,06.

8. Внутренняя норма рентабельности проекта, ее связь с нормой дохода на инвестиции и чистой текущей стоимостью

Нетрудно заметить связь между IRR, NPV и
требуемой нормой дохода на инвестиции (ставкой
дисконтирования). Если I<IRR, NPV положительна, то
есть инвестиционный проект реализуем. Если I>IRR,
NPV отрицательна, то есть инвестиционный проект
непригоден к реализации. Если I=IRR, NPV=0.
Чем больше разница (IRR-I), тем больше «Запас
прочности» проекта, то есть возможность его
реализации с получением запланированной нормы
дохода на инвестиции при условиях повышенного по
сравнению с ожидаемым уровня риска.

9. Модифицированная внутренняя норма рентабельности (MIRR)

В
ряде
случаев
норма
доходности
инвестиций, требуемая инвестором, может по
годам меняться. Кроме того, возможно
привлечение заемных средств под иной
процент, чем норма дохода на инвестиции. В
этом случае показателем эффективности
реализации
проекта
является
модифицированная
внутренняя
норма
рентабельности (MIRR).

10. Модифицированная внутренняя норма рентабельности (MIRR)

Под модифицированной внутренней нормой рентабельности
проекта понимается такая ставка дисконтирования, при которой
будущая стоимость всех доходов на момент окончания срока
реализации инвестпроекта соответствовала бы текущей стоимости
всех первоначальных инвестиций и затрат последующих лет, то есть
соблюдалось бы соотношение:
PV x (1 + MIRR)n = FV, где
PV – сумма дисконтированных на момент оценки потоков расходов,
для каждого из которых в качестве ставки дисконтирования
используется цена привлечения средств;
FV – сумма наращенных на момент окончания срока реализации
проекта потоков доходов, для каждого из которых в качестве ставки
наращения используется требуемая для этого года норма дохода на
инвестиции;
n – срок реализации проекта;
MIRR - Модифицированная внутренняя норма рентабельности
проекта.

11. Модифицированная внутренняя норма рентабельности (MIRR)

Для расчета MIRR используется следующая формула (результат
выражается в долях единицы. Для перевода в проценты
необходимо умножить его на 100).

12. Модифицированная внутренняя норма рентабельности (MIRR)

Рассмотрим следующий пример:
Инвестиционный проект рассчитан на 5 лет. Инвестор вносит
единовременно 120 млн.руб. Кроме того, в течение первых трех лет
потребуются дополнительные инвестиционные затраты по 50
млн.руб. ежегодно, однако для их реализации привлечен кредит
под 8% годовых.
Ожидаемые доходы от проекта:
3-ий год – 40 млн.руб.,
Ставка реинвестирования 15%;
4-ый год – 180 млн.руб.,
Ставка реинвестирования 17%;
5-ый год – 280 млн.руб.,
Ставка реинвестирования 17%.

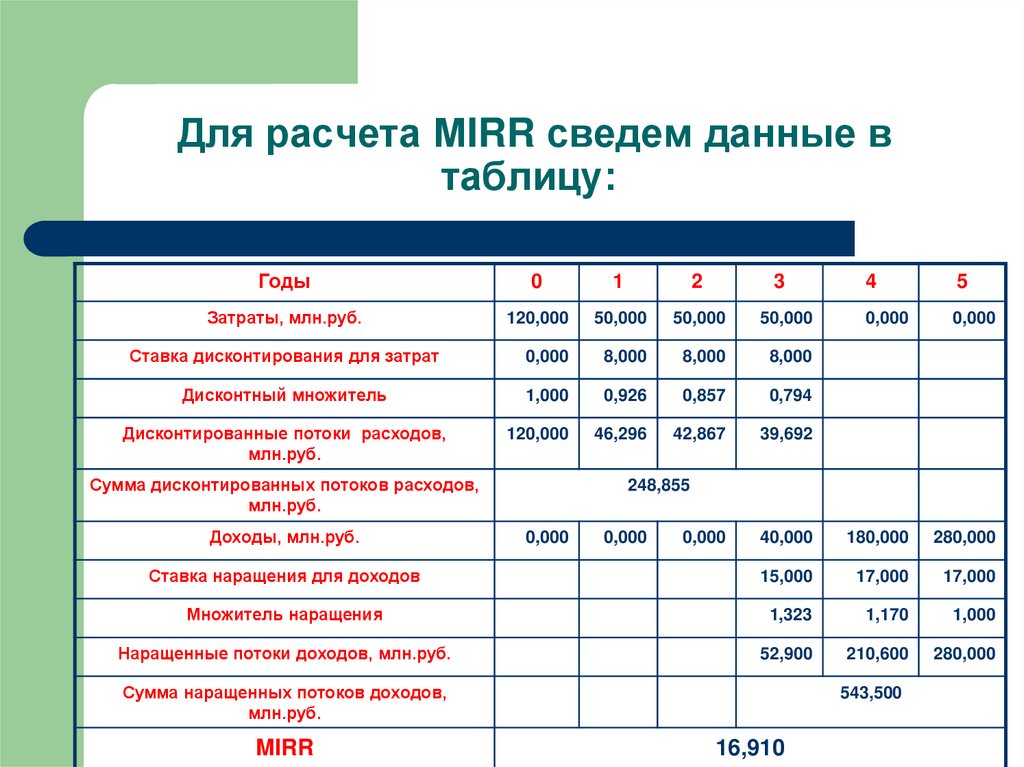
13. Для расчета МIRR сведем данные в таблицу:

Годы
0
1
2
3
Затраты, млн.руб.
120,000
50,000
50,000
50,000
Ставка дисконтирования для затрат
0,000
8,000
8,000
8,000
Дисконтный множитель
1,000
0,926
0,857
0,794
Дисконтированные потоки расходов,
млн.руб.
120,000
46,296
42,867
39,692
4
5
0,000
0,000
40,000
180,000
280,000
Ставка наращения для доходов
15,000
17,000
17,000
Множитель наращения
1,323
1,170
1,000
Наращенные потоки доходов, млн.руб.
52,900
210,600
280,000
Сумма дисконтированных потоков расходов,
млн.руб.
Доходы, млн.руб.
248,855
0,000
0,000
0,000
Сумма наращенных потоков доходов,
млн.руб.
MIRR
543,500
16,910

14. Индексы рентабельности

Индекс рентабельности – это отношение текущей
стоимости проекта (без учета первоначальных
инвестиций) к сумме первоначальных инвестиций.
Различают простой и дисконтированный индексы. Для
расчета
простого
индекса
используется
недисконтированная стоимость проекта, для расчета
дисконтированного индекса – показатель NPV.

15. Индексы рентабельности

Рассчитаем индексы рентабельности по
инвестиционному проекту, для которого
рассчитывались показатели NPV и IRR:
PI простой = 320 / 120 = 2,667
PI дисконтированный (ставка 25%) = 124,608/120 =
1,0384
PI дисконтированный (ставка 27%) = 116,07/120 = 0,967
Таким образом, PI больше единицы при положительном NPV и
меньше единицы при отрицательном.

16. Сроки окупаемости

Как и индексы рентабельности сроки окупаемости
проекта считаются как простые и дисконтированные.
Простой (недисконтированный) срок окупаемости
показывает,
в
какой
момент
кумулятивный
недисконтированный денежный поток сменит знак с
минуса на плюс.
Дисконтированный срок окупаемости показывает, в
какой
момент
кумулятивный
дисконтированный
денежный поток сменит знак с минуса на плюс.

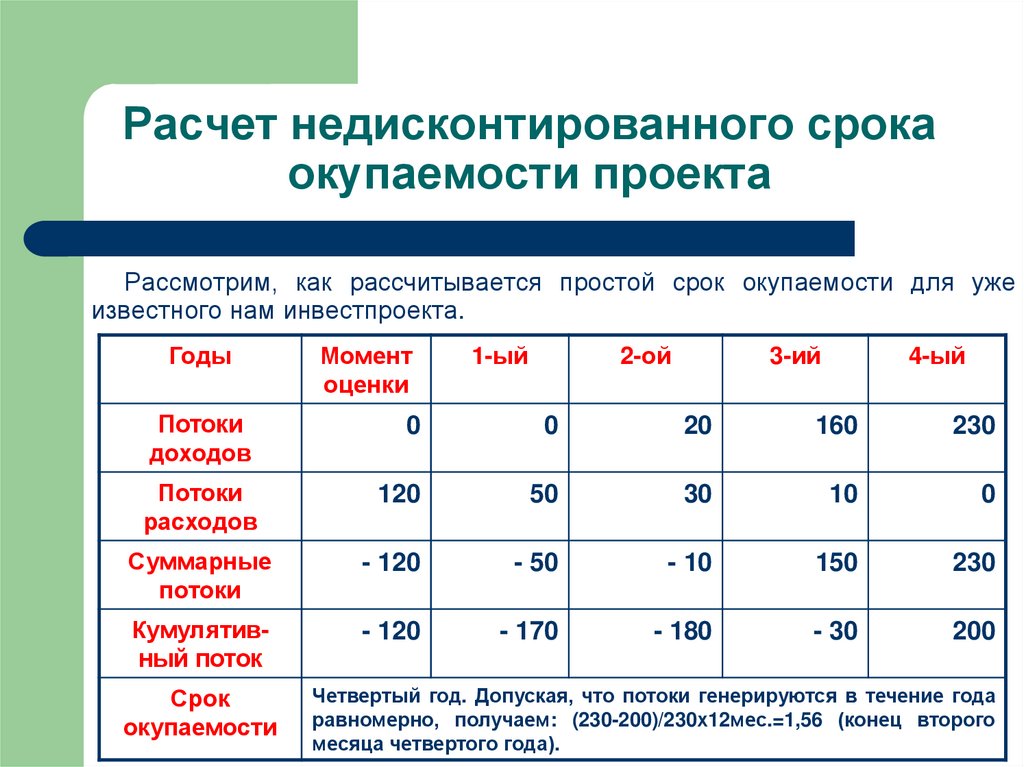
17. Расчет недисконтированного срока окупаемости проекта

Рассмотрим, как рассчитывается простой срок окупаемости для уже
известного нам инвестпроекта.
Годы
Момент
оценки
1-ый
2-ой
3-ий
4-ый
Потоки
доходов
0
0
20
160
230
Потоки
расходов
120
50
30
10
0
Суммарные
потоки
- 120
- 50
- 10
150
230
Кумулятивный поток
- 120
- 170
- 180
- 30
200
Срок
окупаемости
Четвертый год. Допуская, что потоки генерируются в течение года
равномерно, получаем: (230-200)/230х12мес.=1,56 (конец второго
месяца четвертого года).

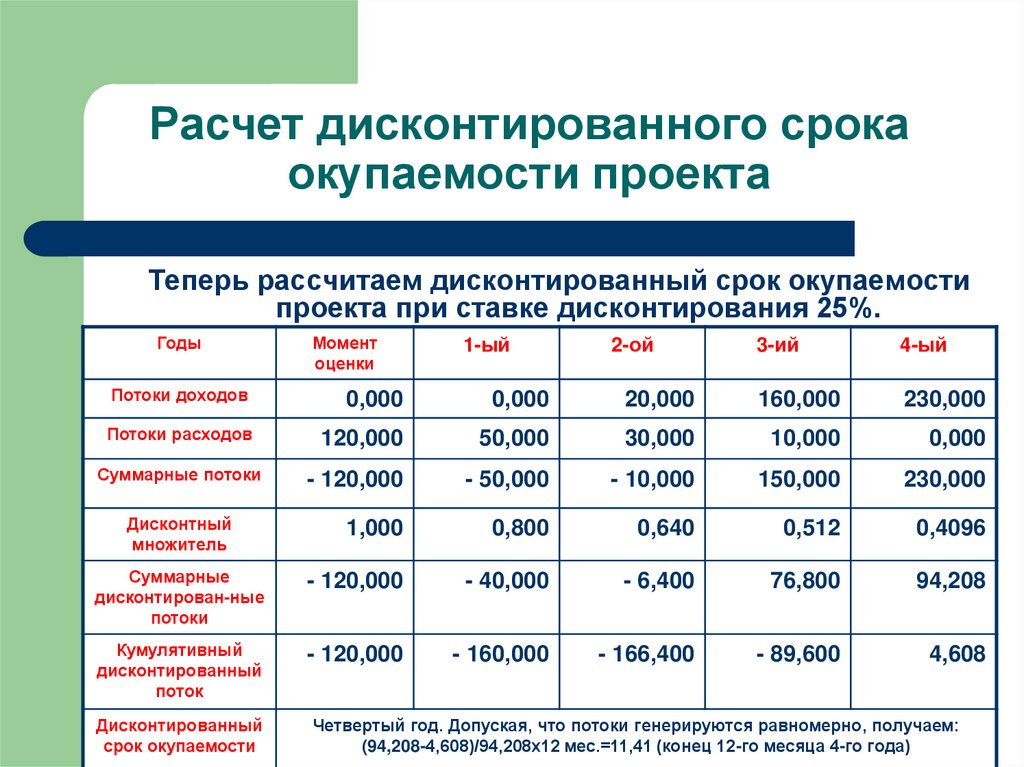
18. Расчет дисконтированного срока окупаемости проекта

Теперь рассчитаем дисконтированный срок окупаемости
проекта при ставке дисконтирования 25%.
Годы
Момент
оценки
1-ый
2-ой
3-ий
4-ый
Потоки доходов
0,000
0,000
20,000
160,000
230,000
Потоки расходов
120,000
50,000
30,000
10,000
0,000
Суммарные потоки
- 120,000
- 50,000
- 10,000
150,000
230,000
1,000
0,800
0,640
0,512
0,4096
Суммарные
дисконтирован-ные
потоки
- 120,000
- 40,000
- 6,400
76,800
94,208
Кумулятивный
дисконтированный
поток
- 120,000
- 160,000
- 166,400
- 89,600
4,608
Дисконтированный
срок окупаемости
Четвертый год. Допуская, что потоки генерируются равномерно, получаем:
(94,208-4,608)/94,208х12 мес.=11,41 (конец 12-го месяца 4-го года)
Дисконтный
множитель

19. Сопоставительный анализ инвестиционных проектов

Если из двух проектов, требующих
одинаковых
первоначальных
инвестиций и рассчитанных на один и
тот же срок, необходимо выбрать для
реализации один, более эффективный,
то при прочих равных условиях следует
предпочесть тот, у которого выше
показатели NPV и IRR.

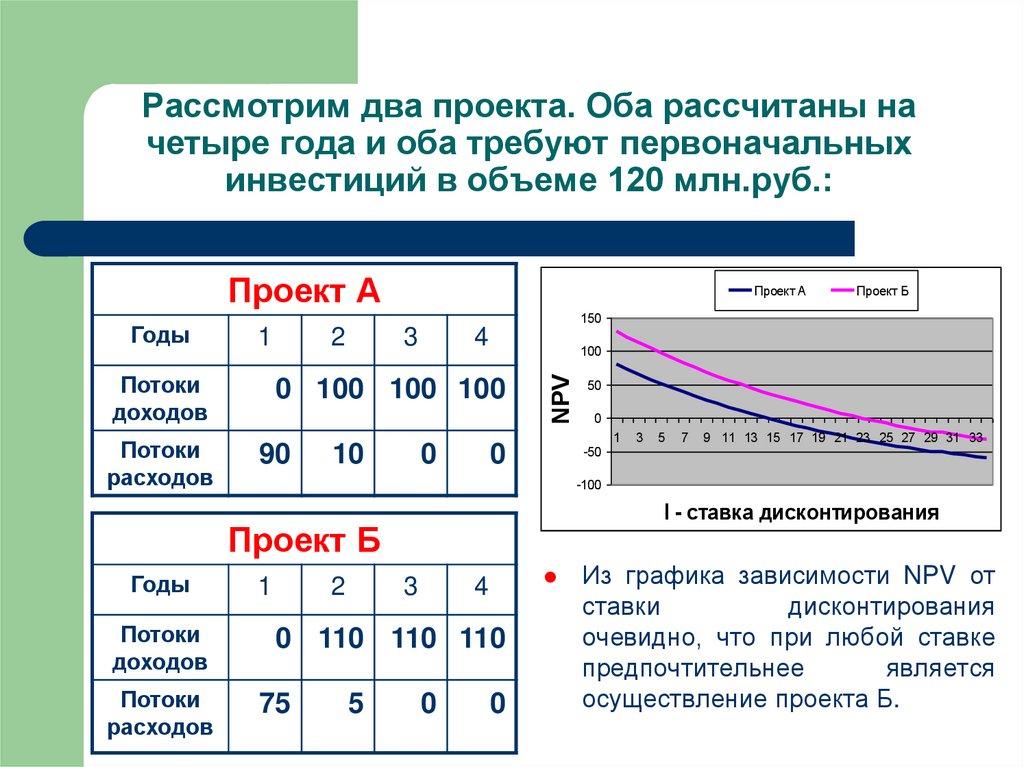
20. Рассмотрим два проекта. Оба рассчитаны на четыре года и оба требуют первоначальных инвестиций в объеме 120 млн.руб.:

Проект А
1
Потоки
доходов
Потоки
расходов
2
3
4
100
0 100 100 100
90
10
0
0
Потоки
доходов
Потоки
расходов
50
0
-50
1
3
5
7
9 11 13 15 17 19 21 23 25 27 29 31 33
-100
I - ставка дисконтирования
Проект Б
Годы
Проект Б
150
NPV
Годы
Проект А
1
2
3
4
0 110 110 110
75
5
0
0
Из графика зависимости NPV от
ставки
дисконтирования
очевидно, что при любой ставке
предпочтительнее
является
осуществление проекта Б.

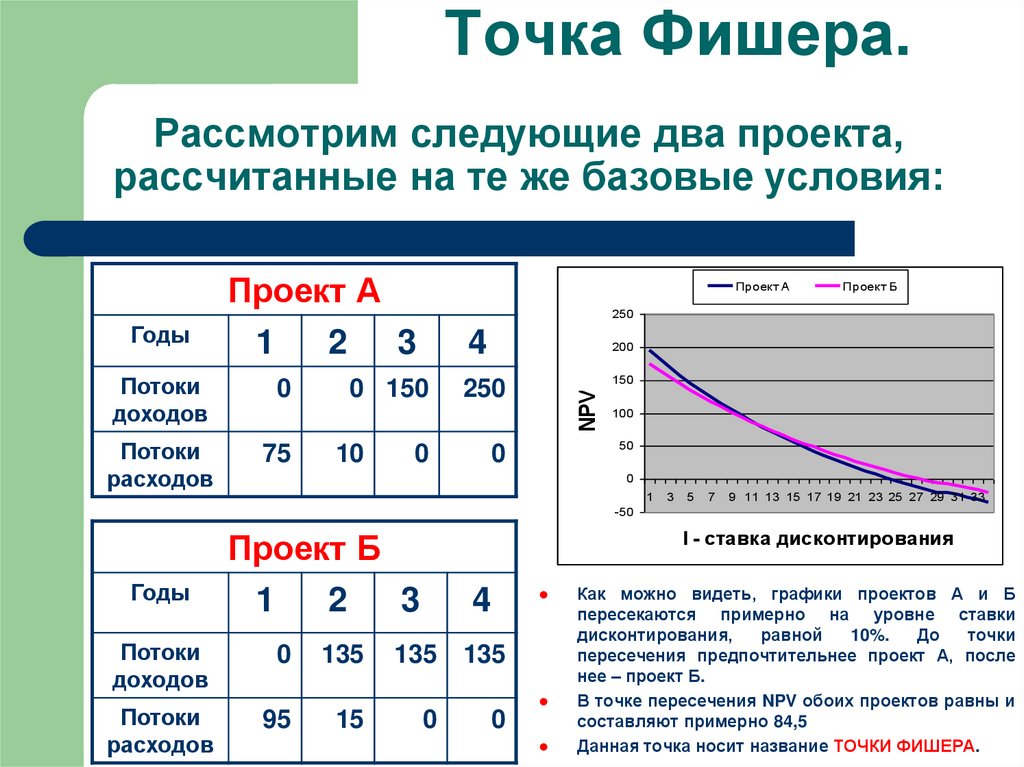
21. Точка Фишера. Рассмотрим следующие два проекта, рассчитанные на те же базовые условия:

Проект А
1
2
Потоки
доходов
0
Потоки
расходов
75
3
4
0 150
250
10
Проект Б
250
0
200
150
NPV
Годы
Проект А
100
50
0
0
1
3
5
7
9 11 13 15 17 19 21 23 25 27 29 31 33
-50
Годы
I - ставка дисконтирования
Проект Б
1
2
3
4
Потоки
доходов
0
135
135
135
Потоки
расходов
95
15
0
0
Как можно видеть, графики проектов А и Б
пересекаются примерно на уровне ставки
дисконтирования,
равной
10%.
До
точки
пересечения предпочтительнее проект А, после
нее – проект Б.
В точке пересечения NPV обоих проектов равны и
составляют примерно 84,5
Данная точка носит название ТОЧКИ ФИШЕРА.

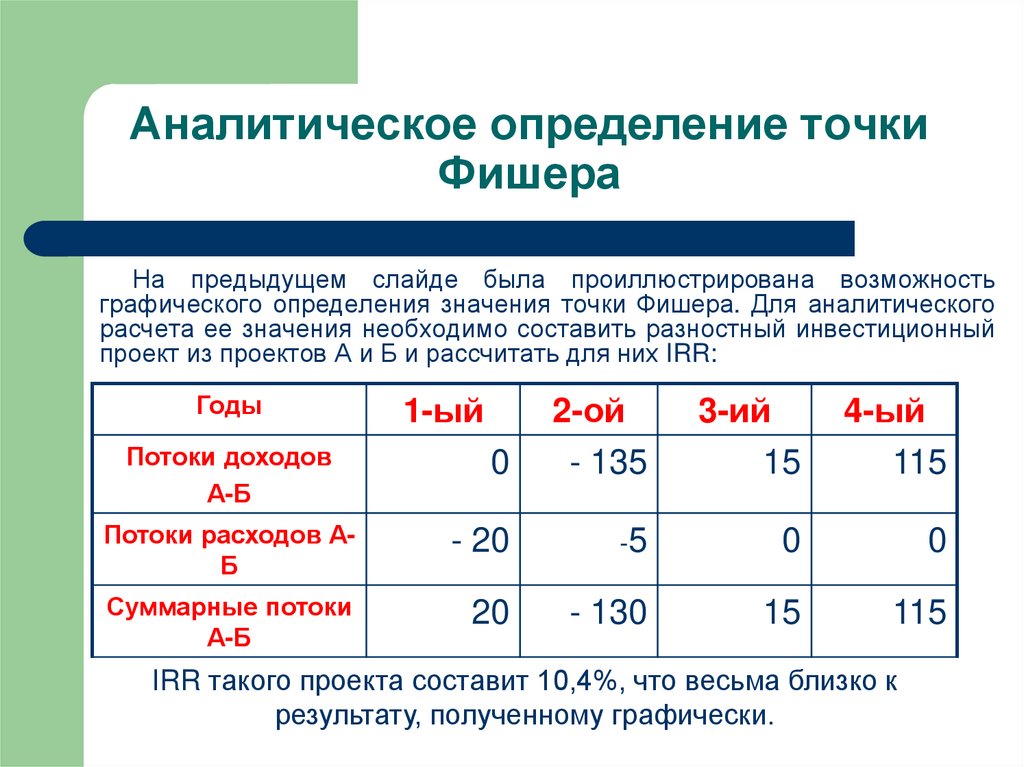
22. Аналитическое определение точки Фишера

На предыдущем слайде была проиллюстрирована возможность
графического определения значения точки Фишера. Для аналитического
расчета ее значения необходимо составить разностный инвестиционный
проект из проектов А и Б и рассчитать для них IRR:
Годы
0
2-ой
- 135
3-ий
15
4-ый
115
Потоки расходов АБ
- 20
-5
0
0
Суммарные потоки
А-Б
20
- 130
15
115
Потоки доходов
А-Б
1-ый
IRR такого проекта составит 10,4%, что весьма близко к
результату, полученному графически.