Похожие презентации:
Матрицы. Основные определения
1.
§4. Матрицып.1. Основные определения.
Матрицей порядка (размерности) m n
называется прямоугольная таблица чисел,
состоящая из m строк и n столбцов.
Обозначается:
a11 a12
A, Am n ,
a21 a22
a
m1 am 2
a1n
a2 n
.
amn
aij ─ элемент матрицы: i ─ номер строки, j ─
номер столбца.
2.
Пример.2 3 1
.
Am n
0 7 1.3
m ?2 n ?3
0 ?a21
3.
Две матрицы называются равными междусобой, если равны их все соответствующие
элементы.
Замечание 1.
Для матриц не вводятся понятия «больше» и
«меньше».
4.
Матрица AT называетсятранспонированной к матрице A, если
строки матрицы A являются столбцами
матрицы AT.
Пример.
2 0
T
A 3 7 .
1 1.3
2 3 1
,
A
0 7 1.3
Замечание 2.
A A.
T T
5.
Если AT = A, то матрица A называетсясимметричной.
Пример.
0
1 2
6 .
2 8
0 6 3
Матрица называется нулевой, если все ее
элементы равны нулю.
0 0 0
.
O
0 0 0
6.
Квадратной матрицей называется матрица,у которой число строк равно числу столбцов.
Пример.
главная
диагональ
0
1 2
6
2 8
0 2 3
побочная
диагональ
7.
Квадратная матрица, все элементы которойкроме элементов, расположенных на главной
диагонали, равны нулю, называется
диагональной.
Диагональная матрица, у которой каждый
элемент, расположенный на главной
диагонали, равен единице, называется
единичной.
Пример.
3 0 0
A 0 1 0
0 0 2
1 0 0
E 0 1 0
0 0 1
8.
Квадратная матрица называется треугольной,если все элементы, расположенные по одну
сторону от главной диагонали, равны нулю.
Пример.
5
1 2
6 .
0 8
0 0 3
9.
п.2. Действия над матрицами1) Сложение.
Складывать можно матрицы одного порядка.
Am n Bm n Cm n
Суммой двух матриц Am n и Bm n называется
матрица Cm n , каждый элемент которой
равен сумме соответствующих элементов
исходных матриц.
cij aij bij , i 1, m, j 1, n.
10.
Пример.2 3 1 1 0 1 ?3 3? 0
0 7 4 2 3 5 2 10 9
11.
2) Вычитание.Пример.
2 3 1 1 0 1 1? 1 ? 3 2
0 7 4 2 3 55 2 4 1
Самостоятельно: дать определение.
12.
3) Умножение матрицы на число.Результатом умножения матрицы Am nна
число называется матрица Bm n,
каждый элемент которой равен произведению
данного числа и соответствующего элемента
исходной матрицы.
bij aij , i 1, m, j 1, n.
13.
Пример.2 3 1 ?4 ?6 2
2
0 7 4 0 14 8
14.
Свойства операций сложения матриц иумножения на число
Пусть A, B, C — матрицы, , R.
1) A B B A.
2) A ( B C ) ( A B) C.
3) A O A.
4) A A O.
5) 1 A A.
6) ( A B) A B.
7) ( ) A A A.
8) ( A) ( ) A.
9) ( A B) A B .
T
T
T
15.
4) Умножение матрицы на матрицу.Am n Bn k Cm k
Произведением двух матриц Am n и Bn k
называется матрица Cm k , каждый элемент
которой cij равен сумме произведений
элементов i-й строки матрицы Am n
и j-го столбца матрицы Bn k.
n
cij
l 1
ail blj , i 1, m,
j 1, k .
16.
Пример.2 3 1 1 0 1
0 7 4 2 3 5
A2 3
B2 3
Матрицы умножать нельзя.
17.
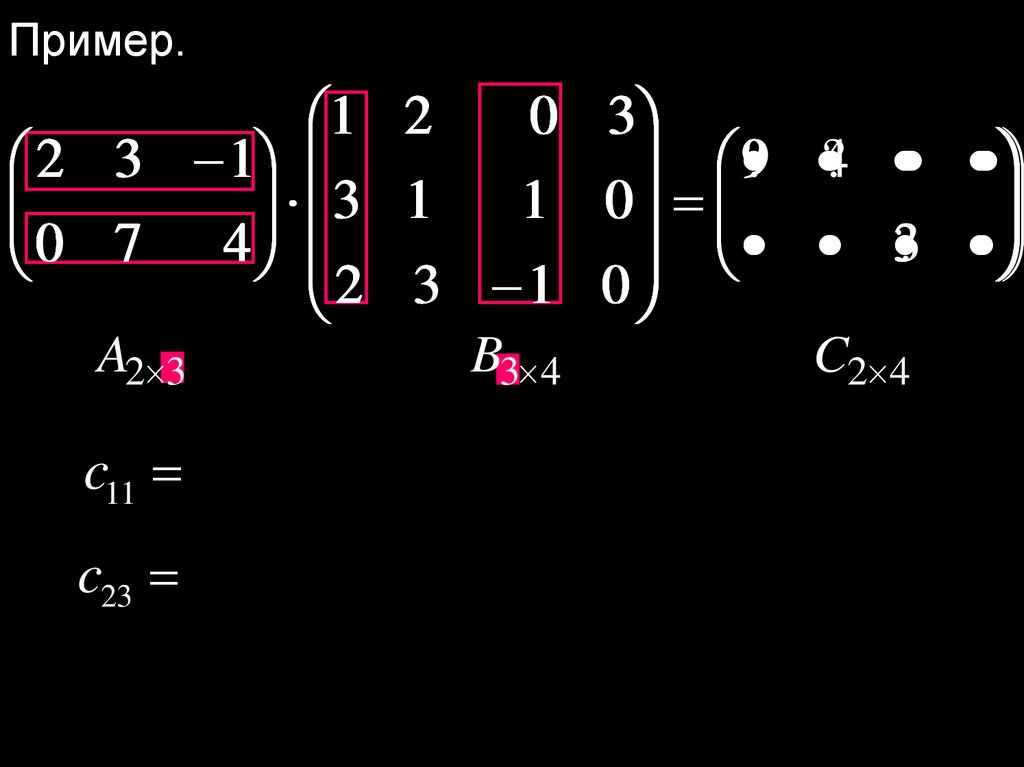
Пример.0 3
1 2
9? ?4
2 3 1
3 1
1 0
0 7 4 2 3 1 0 ? 3
A2 3
B3 4
c11 2 1 3 3 ( 1) 2 9
c23 0 0 7 1 4 ( 1) 3
C2 4
18.
Замечание 3.AB BA.
Пример.
A2 3 B3 4 умножать можно
B3 4 A2 3 умножать нельзя
Пример.
0 1
3
1 2 0
A 2
1 1 , B 2 1 4 .
0 1 1
1 2 2
7 2 7
AB 4
0
7 ,
1 0 11
4 4 2
BA 4 13 9 .
1 1 1
19.
Свойства операции умножения матрицПусть A, B, C — матрицы, R.
1) A E E A A.
2) A ( B C ) ( A B) C.
3) A ( B C ) AB AC.
4) ( A B) C AC BC .
5) ( AB) ( A) B.
T
T
T
6) ( AB) B A .












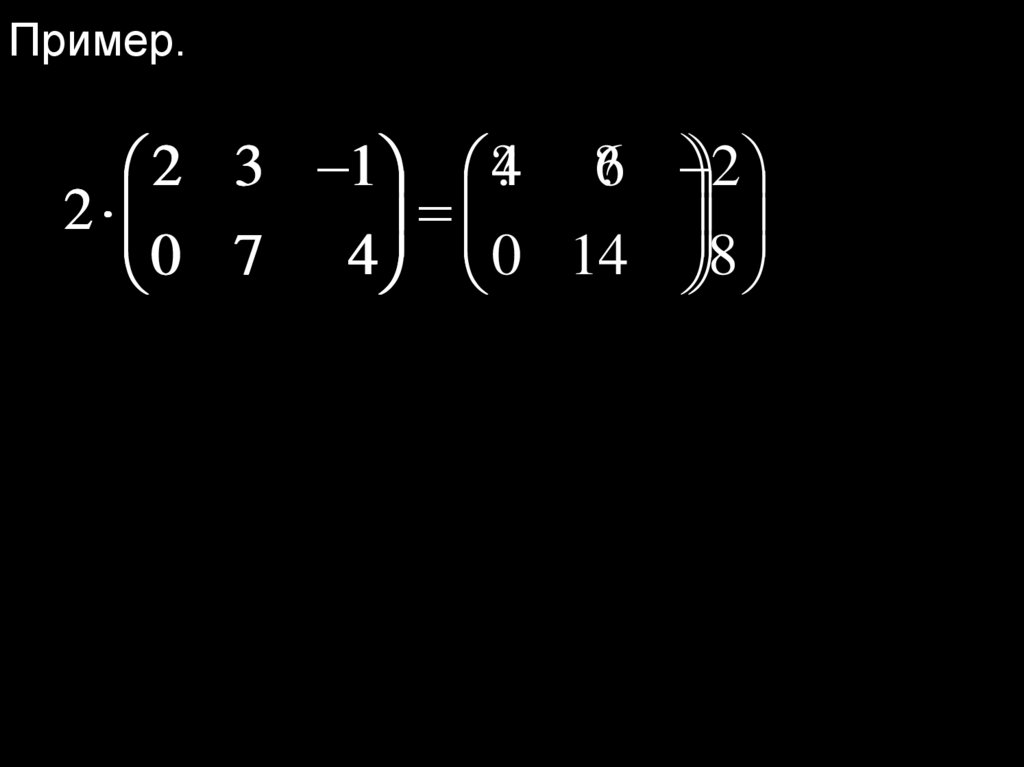





 Математика
Математика








